天津市天津一中2012届高三入学摸底考试 理科数学试题
文档属性
| 名称 | 天津市天津一中2012届高三入学摸底考试 理科数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 134.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-10 10:43:34 | ||
图片预览




文档简介
天津一中2011—2012学年高三数学摸底试卷(理科)
一、选择题:
1.是虚数单位,的值是
A. B. C. D.
2.某学校有高中学生900人,其中高一有400人,高二300人,高三200人,采用分层抽样的方法抽取一个容量为45的样本,那么高一、高二、高三各年级抽取的学生人数为
A. 25、15、5 B. 20、15、10 C. 30、10、5 D.15、15、15
3.已知集合,则的充要条件是
A. B. C. D.
4. 要得到函数的图像,只需将函数图像上的所有点
A.横坐标伸长到原来的3倍,纵坐标不变 B.横坐标缩短到原来的,纵坐标不变
C.横坐标伸长到原来的倍,纵坐标不变 D.横坐标缩短到原来的,纵坐标不变
5.若某空间几何体的三视图如图所示,则该几何体的体积是
A.2 B.1
C. D.
6.设是等差数列的前项和,若
A.2 B.-1 C.1 D.
7.如图,三行三列的方阵中有9个数,从中任取三个数,则至少有两个数位于同行或同列的概率是
A. B. C. D.
8.设,若是与的等比中项,则的最小值为
A.8 B.4 C.1 D.
二、填空题:
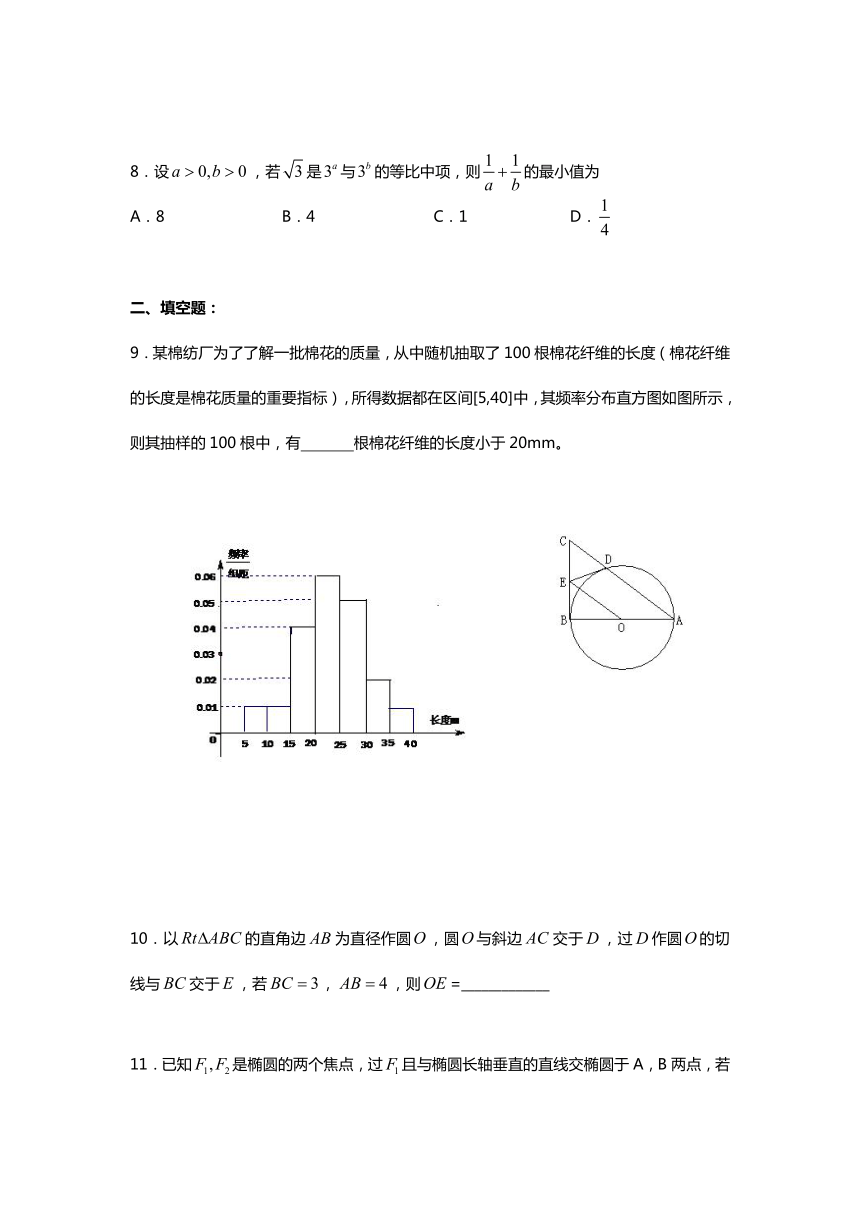
9.某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示,则其抽样的100根中,有 根棉花纤维的长度小于20mm。
10.以的直角边为直径作圆,圆与斜边交于,过作圆的切线与交于,若,,则=_____________
11.已知是椭圆的两个焦点,过且与椭圆长轴垂直的直线交椭圆于A,B两点,若是正三角形,则这个椭圆的离心率是
12. 在直角坐标系中,直线的参数方程为 (为参数),若以为极点,轴正半轴为极轴建立极坐标系,则曲线的极坐标方程为,则直线被曲线所截得的弦长为
13.已知函数在区间上是增函数,则实数的取值范围是
14.在中,为中线上一个动点,若,则的最小值是
三、解答题:
15.如图,圆的直径的延长线与弦的延长线相交于点,为圆上一点,交于点,且
(1)求线段的长度
(2)若圆与圆内切,直线与圆切于点,
求线段的长度
16.在中,角所对应的边分别为,且,
(1)求角的大小
(2)若, 求的面积
17.设数列是公差大于0的等差数列,分别是方程的两个实根
(1)求数列的通项公式
(2)设,求数列的前项和
18.口袋里装有大小相同的卡片八张,其中三张标有数字1,三张标有数字2,二张标有数字3,第一次从口袋里任里任意抽取一张,放回口袋里后第二次再任意抽取一张,记第一次与第二次取到卡片上数字之和为.
(1)为何值时,其发生的概率最大?说明理由;
(2)求随机变量的期望.
19.椭圆的离心率为,长轴的端点与短轴的端点间的距离为
(1)求椭圆的方程
(2)设过点的直线与椭圆交于两点,为坐标原点,若△为直角三角形,求直线的斜率。
20.已知函数
(1)当时,求的极值
(2)当时,求的单调区间
(3)若对任意的,恒有成立,求实数的取值范围。
参考答案
一、选择题
1.A 2.B 3.A 4.D 5.B 6.C 7.D 8.B
二、填空题
9.30 10.
11. 12.
13.[,2] 14.-2
三、解答题
15.解:
(1)∵∠AOC=∠P+∠PCO
∠EDC=∠P+∠PFD
∴∠PCO=∠PFD
∴△PFD∽△PCD
∴
∴PO PF=PC PD
PO PF=PB PA
PF=3
(2)OF=2-
PT2=PB PD=2×4
∴PT=
16.解:
17.解:(1){an}公差d>0可知a3即
(2)bn=
两式相减:
18.解
(1)取值为2,3,4,5,6
19.解
椭圆方程为
(4k2+1)x2+32kx+60=0
△=(32k)2-240(1+4k2)>0
20.解
↘ 极小值 ↗
一、选择题:
1.是虚数单位,的值是
A. B. C. D.
2.某学校有高中学生900人,其中高一有400人,高二300人,高三200人,采用分层抽样的方法抽取一个容量为45的样本,那么高一、高二、高三各年级抽取的学生人数为
A. 25、15、5 B. 20、15、10 C. 30、10、5 D.15、15、15
3.已知集合,则的充要条件是
A. B. C. D.
4. 要得到函数的图像,只需将函数图像上的所有点
A.横坐标伸长到原来的3倍,纵坐标不变 B.横坐标缩短到原来的,纵坐标不变
C.横坐标伸长到原来的倍,纵坐标不变 D.横坐标缩短到原来的,纵坐标不变
5.若某空间几何体的三视图如图所示,则该几何体的体积是
A.2 B.1
C. D.
6.设是等差数列的前项和,若
A.2 B.-1 C.1 D.
7.如图,三行三列的方阵中有9个数,从中任取三个数,则至少有两个数位于同行或同列的概率是
A. B. C. D.
8.设,若是与的等比中项,则的最小值为
A.8 B.4 C.1 D.
二、填空题:
9.某棉纺厂为了了解一批棉花的质量,从中随机抽取了100根棉花纤维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示,则其抽样的100根中,有 根棉花纤维的长度小于20mm。
10.以的直角边为直径作圆,圆与斜边交于,过作圆的切线与交于,若,,则=_____________
11.已知是椭圆的两个焦点,过且与椭圆长轴垂直的直线交椭圆于A,B两点,若是正三角形,则这个椭圆的离心率是
12. 在直角坐标系中,直线的参数方程为 (为参数),若以为极点,轴正半轴为极轴建立极坐标系,则曲线的极坐标方程为,则直线被曲线所截得的弦长为
13.已知函数在区间上是增函数,则实数的取值范围是
14.在中,为中线上一个动点,若,则的最小值是
三、解答题:
15.如图,圆的直径的延长线与弦的延长线相交于点,为圆上一点,交于点,且
(1)求线段的长度
(2)若圆与圆内切,直线与圆切于点,
求线段的长度
16.在中,角所对应的边分别为,且,
(1)求角的大小
(2)若, 求的面积
17.设数列是公差大于0的等差数列,分别是方程的两个实根
(1)求数列的通项公式
(2)设,求数列的前项和
18.口袋里装有大小相同的卡片八张,其中三张标有数字1,三张标有数字2,二张标有数字3,第一次从口袋里任里任意抽取一张,放回口袋里后第二次再任意抽取一张,记第一次与第二次取到卡片上数字之和为.
(1)为何值时,其发生的概率最大?说明理由;
(2)求随机变量的期望.
19.椭圆的离心率为,长轴的端点与短轴的端点间的距离为
(1)求椭圆的方程
(2)设过点的直线与椭圆交于两点,为坐标原点,若△为直角三角形,求直线的斜率。
20.已知函数
(1)当时,求的极值
(2)当时,求的单调区间
(3)若对任意的,恒有成立,求实数的取值范围。
参考答案
一、选择题
1.A 2.B 3.A 4.D 5.B 6.C 7.D 8.B
二、填空题
9.30 10.
11. 12.
13.[,2] 14.-2
三、解答题
15.解:
(1)∵∠AOC=∠P+∠PCO
∠EDC=∠P+∠PFD
∴∠PCO=∠PFD
∴△PFD∽△PCD
∴
∴PO PF=PC PD
PO PF=PB PA
PF=3
(2)OF=2-
PT2=PB PD=2×4
∴PT=
16.解:
17.解:(1){an}公差d>0可知a3
(2)bn=
两式相减:
18.解
(1)取值为2,3,4,5,6
19.解
椭圆方程为
(4k2+1)x2+32kx+60=0
△=(32k)2-240(1+4k2)>0
20.解
↘ 极小值 ↗
同课章节目录
