2020-2021学年七年级数学苏科版下册《9.4 乘法公式》强化提优检测(2)(Word版 含答案)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册《9.4 乘法公式》强化提优检测(2)(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 349.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 00:00:00 | ||
图片预览




文档简介
苏科版七年级下册《9.4
乘法公式》强化提优检测(2)
(时间:60分钟
满分:120分)
1.选择题(共20题;共40分)
1.计算(x-5)2=( )
A.x2-25
B.x2+25
C.x2-5x+25
D.x2-10x+25
2.已知2a-3b+4c=2a-( )成立,则括号内应填的项是( )
A.-3b+4c
B.3b-4c
C.-3b-4c
D.3b+4c
3.
应用公式(a+b)(a-b)=a2-b2计算(x+2y-1)(x-2y+1),下列变形正确的是( )
A.[x-(2y+1)]2
B.[x+(2y+1)]2
C.[x-(2y-1)][x+(2y-1)]
D.[(x-2y)+1][(x-2y)-1]
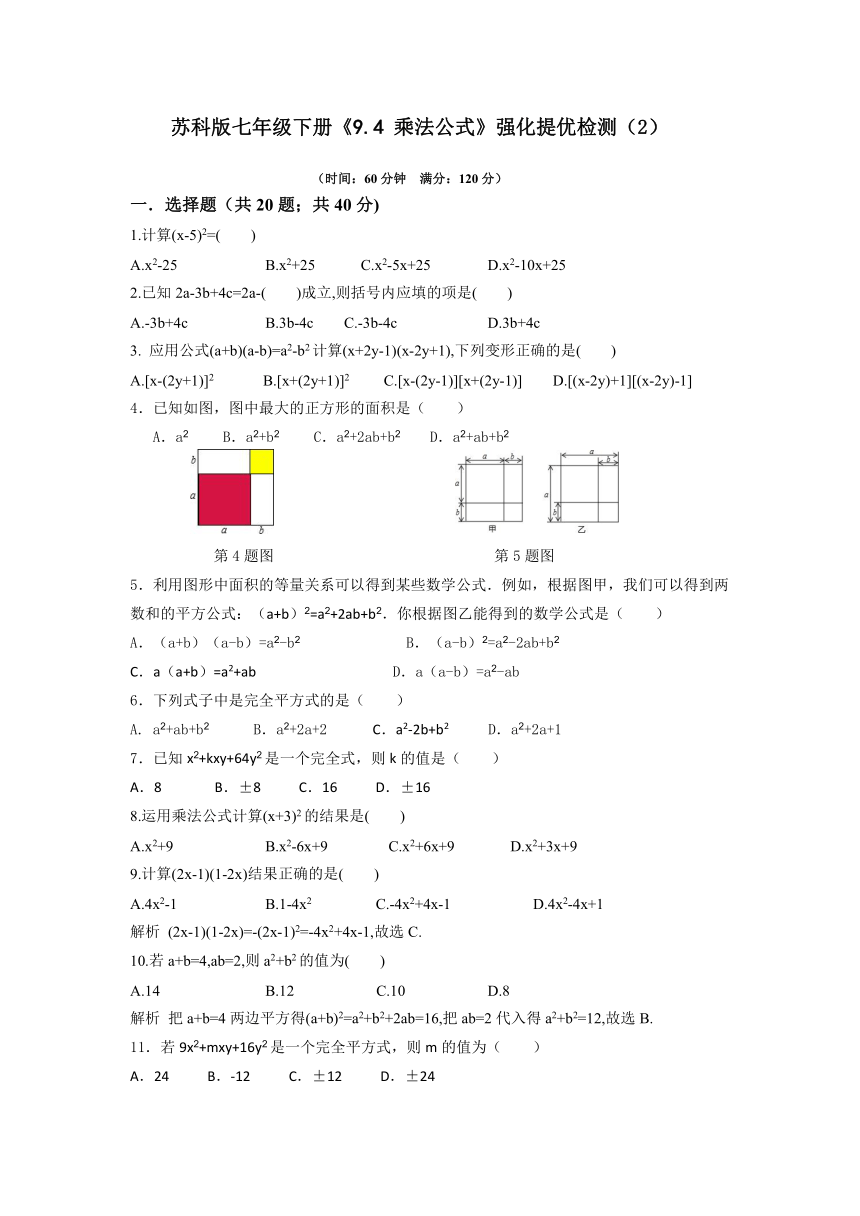
4.已知如图,图中最大的正方形的面积是( )
A.a2
B.a2+b2
C.a2+2ab+b2
D.a2+ab+b2
第4题图
第5题图
5.利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )
A.(a+b)(a-b)=a2-b2
B.(a-b)2=a2-2ab+b2
C.a(a+b)=a2+ab
D.a(a-b)=a2-ab
6.下列式子中是完全平方式的是( )
A.
a2+ab+b2
B.a2+2a+2
C.a2-2b+b2
D.a2+2a+1
7.已知x2+kxy+64y2是一个完全式,则k的值是( )
A.8
B.±8
C.16
D.±16
8.运用乘法公式计算(x+3)2的结果是( )
A.x2+9
B.x2-6x+9
C.x2+6x+9
D.x2+3x+9
9.计算(2x-1)(1-2x)结果正确的是( )
A.4x2-1
B.1-4x2
C.-4x2+4x-1
D.4x2-4x+1
解析
(2x-1)(1-2x)=-(2x-1)2=-4x2+4x-1,故选C.
10.若a+b=4,ab=2,则a2+b2的值为( )
A.14
B.12
C.10
D.8
解析
把a+b=4两边平方得(a+b)2=a2+b2+2ab=16,把ab=2代入得a2+b2=12,故选B.
11.若9x2+mxy+16y2是一个完全平方式,则m的值为( )
A.24
B.-12
C.±12
D.±24
12.下列多项式中是完全平方式的是( )
A.2x2+4x-4
B.16x2-8y2+1
C.9a2-12a+4
D.x2y2+2xy+y2
13.下列各式中计算正确的是( )
A.(a-b)2=a2-b2
B.(a+2b)2=a2+2ab+4b2
C.(a2+1)2=a4+2a+1
D.(-m-n)2=m2+2mn+n2
14.设(5a+3b)2=(5a-3b)2+A,则A=( )
A.30ab
B.60ab
C.15ab
D.12ab
15、若二次三项式是一个完全平方式,则的值为(??
).
?A.
?B.
C.
?D.
16、填空:___________.---------
(
)
?A.
,
?B.
,
?C.
,
?D.
,
17、在多项式中添加一个单项式,使其成为一个完全平方式,则添加的单项式可以是( )
A.
??B.
???C.
?D.
18.
已知(x-2
019)2+(x-2
021)2=34,则(x-2
020)2的值是( )
A.4
B.8
C.12
D.16
19、已知多项式是一个完全平方式,则的值是(?
)
?A.
14
??B.
-10
??C.
或
??D.
或
20.不论a
b为任何有理数,则a2
+b2
-4a
+2b+7的值总是(
?
).
?A.
负数
??B.
零
??C.
可以为任一正数
??D.
不小于
2.填空题(共10题;共20分)
21.
若(7x-a)2=49x2-bx+9,则|a+b|= .?
22、????????????????????????.
23.若把代数式x2-2x-3化为(x-m)2+k的形式,其中m,k为常数,则m+k=
-3
.
24.若(x+
)2=9,则(x
-
)2的值为
.
25.已知x+y=7且xy=12,则当x<y时,-
的值等于
.
26.若a2+b2=5,ab=2,则(a+b)2=
.
28.已知x+y=1,则x2+xy+y2=
.
29、已知,则的值是????????????.
30、已知,则_________.
3、解答题(共8题;共40分)
31(8分)计算
(1):x(x+1)-(x-1)2.
(2)2x(x-2y)-(2x-y)2
32.(8分)已知x+2y=6,x2+4y2=20,求下列各式的值:
(1)xy;
(2)(x-2y)2.
33.(6分)先化简,再求值:(x-2y)(x+2y)-(2x-y)2+(x+2y)2,其中,x=-1,y=-2.
34.(6分)图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)将图②中的阴影部分面积用两种方法表示可得一个等式,这个等式为 .?
(2)若m+2n=7,mn=3,利用(1)的结论求m-2n的值.
35.
(4分)已知(a+b)2=25,(a-b)2=9,求ab与a2+b2的值.
36.
(4分)已知(x+y)2=1,(x-y)2=49,求x2+y2与xy的值.
37.(4分)已知x,y互为相反数,且(x+3)2-(y+3)2=6,求x,y的值.
38.(8分)如图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状围成一个正方形.
(1)图②中的阴影部分面积为 .?
(2)观察图②,请你写出(m+n)2,(m-n)2,mn之间的等量关系是 .?
(3)实际上有许多恒等式可以用图形的面积来表示,如图③,它表示了 .?
(4)试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.(在图中标出相应的长度)
教师样卷
一.选择题(共20题;共40分)
1.计算(x-5)2=( D )
A.x2-25
B.x2+25
C.x2-5x+25
D.x2-10x+25
2.已知2a-3b+4c=2a-( )成立,则括号内应填的项是( B )
A.-3b+4c
B.3b-4c
C.-3b-4c
D.3b+4c
解析
直接利用添括号法则求出即可,2a-3b+4c=2a-(3b-4c).故选B.
4.
应用公式(a+b)(a-b)=a2-b2计算(x+2y-1)(x-2y+1),下列变形正确的是( C )
A.[x-(2y+1)]2
B.[x+(2y+1)]2
C.[x-(2y-1)][x+(2y-1)]
D.[(x-2y)+1][(x-2y)-1]
解析
(x+2y-1)(x-2y+1)=[x-(2y-1)]·[x+(2y-1)].故选C.
4.已知如图,图中最大的正方形的面积是( C )
A.a2
B.a2+b2
C.a2+2ab+b2
D.a2+ab+b2
第4题图
第5题图
5.利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( B )
A.(a+b)(a-b)=a2-b2
B.(a-b)2=a2-2ab+b2
C.a(a+b)=a2+ab
D.a(a-b)=a2-ab
6.下列式子中是完全平方式的是( D )
A.
a2+ab+b2
B.a2+2a+2
C.a2-2b+b2
D.a2+2a+1
7.已知x2+kxy+64y2是一个完全式,则k的值是( D )
A.8
B.±8
C.16
D.±16
8.运用乘法公式计算(x+3)2的结果是( C )
A.x2+9
B.x2-6x+9
C.x2+6x+9
D.x2+3x+9
9.计算(2x-1)(1-2x)结果正确的是( C )
A.4x2-1
B.1-4x2
C.-4x2+4x-1
D.4x2-4x+1
解析
(2x-1)(1-2x)=-(2x-1)2=-4x2+4x-1,故选C.
10.若a+b=4,ab=2,则a2+b2的值为( B )
A.14
B.12
C.10
D.8
解析
把a+b=4两边平方得(a+b)2=a2+b2+2ab=16,把ab=2代入得a2+b2=12,故选B.
11.若9x2+mxy+16y2是一个完全平方式,则m的值为( D )
A.24
B.-12
C.±12
D.±24
12.下列多项式中是完全平方式的是( C )
A.2x2+4x-4
B.16x2-8y2+1
C.9a2-12a+4
D.x2y2+2xy+y2
13.下列各式中计算正确的是( D )
A.(a-b)2=a2-b2
B.(a+2b)2=a2+2ab+4b2
C.(a2+1)2=a4+2a+1
D.(-m-n)2=m2+2mn+n2
解析
选项A,应为(a-b)2=a2-2ab+b2,故本选项错误;选项B,应为(a+2b)2=a2+4ab+4b2,故本选项错误;选项C,应为(a2+1)2=a4+2a2+1,故本选项错误;选项D,(-m-n)2=m2+2mn+n2,正确.故选D.
14.设(5a+3b)2=(5a-3b)2+A,则A=( B )
A.30ab
B.60ab
C.15ab
D.12ab
解析
∵(5a+3b)2=(5a-3b)2+A,∴A=(5a+3b)2-(5a-3b)2=(5a+3b+5a-3b)(5a+3b-5a+3b)=60ab.故选B.
15、若二次三项式是一个完全平方式,则的值为(??C?
).
?A.
?B.
C.
?D.
解:
又是一个完全平方式,,.故答案选:.
16、填空:___________.---------
(
A
)
?A.
,
?B.
,
?C.
,
?D.
,
解:,.
故答案应选:,.
17、在多项式中添加一个单项式,使其成为一个完全平方式,则添加的单项式可以是( C )
A.
??B.
???C.
?D.
【解析】①若为平方项,则加上的项是:;②若为乘积二倍项,
则加上的项是:;③若加上后是单项式的平方,则加上的项是:或.
故为:或或或或.
19.
已知(x-2
019)2+(x-2
021)2=34,则(x-2
020)2的值是( B )
A.4
B.8
C.12
D.16
解析
∵(x-2
019)2+(x-2
021)2=34,∴(x-2
020+1)2+(x-2
020-1)2=34.
∴(x-2
020)2+2(x-2
020)+1+(x-2
020)2-2(x-2
020)+1=34.∴2(x-2
020)2+2=34.∴2(x-2
020)2=32.∴(x-2
020)2=16.故选D.
19、已知多项式是一个完全平方式,则的值是(?
C
)
?A.
14
??B.
-10
??C.
或
??D.
或
20.不论a
b为任何有理数,则a2
+b2
-4a
+2b+7的值总是(
D?
).
?A.
负数
??B.
零
??C.
可以为任一正数
??D.
不小于
3.填空题(共10题;共20分)
22.
若(7x-a)2=49x2-bx+9,则|a+b|= .?
【答案】.45 解析
∵(7x-a)2=49x2-bx+9,∴49x2-14ax+a2=49x2-bx+9.∴-14a=-b,a2=9.解得a=3,b=42或a=-3,b=-42.当a=3,b=42时,|a+b|=|3+42|=45;当a=-3,b=-42时,|a+b|=|-3-42|=45.故答案为45.
22、????????????????????????.
【答案】,.
【解析】,
故答案是:,.
23.若把代数式x2-2x-3化为(x-m)2+k的形式,其中m,k为常数,则m+k=
-3
.
【答案】-3
解
:
根据完全平方公式的结构,按照要求x2-2x-3=x2-2x+1-4=(x-1)2-4,可知m=1.k=-4,则m+k=-3.∵x2-2x-3=x2-2x+1-4=(x-1)2-4,∴m=1,k=
-4,∴m+k=-3.故填-3.
24.若(x+
)2=9,则(x
-
)2的值为
.
【答案】5
25.已知x+y=7且xy=12,则当x<y时,-
的值等于
.
【答案】
解:
先运用完全平方公式的变形求出y-x的值,然后代入通分后的所求式子中,计算即可.∵x+y=7且xy=12,∴(x-y)2=(x+y)2-4xy=72-4×12=49-48=1,
∵x<y,∴y-x=1,
∴-
==.
26.若a2+b2=5,ab=2,则(a+b)2=
.
【答案】9
28.已知x+y=1,则x2+xy+y2=
.
【答案】
29、已知,则的值是????????????.
【答案】28
【解析】:,
故答案为:
30、已知,则_________.
【答案】
【解析】:原式可化为,即;∴,,即,.
因此,,.故答案为:.
4、解答题(共8题;共40分)
31.(8分)计算
(1):x(x+1)-(x-1)2.
(2)2x(x-2y)-(2x-y)2
解(1)
x(x+1)-(x-1)2=x2+x-x2+2x-1=3x-1.
(2)2x(x-2y)-(2x-y)2=2x2-4xy-(4x2-4xy+y2)=2x2-4xy-4x2+4xy-y2=-2x2-y2.
32.(8分)已知x+2y=6,x2+4y2=20,求下列各式的值:
(1)xy;
(2)(x-2y)2.
解
(1)∵x+2y=6,∴(x+2y)2=62.∴x2+4xy+4y2=36.∵x2+4y2=20,∴4xy=16.∴xy=4.
(2)∵x2+4y2=20,xy=4,∴(x-2y)2=x2-4xy+4y2=20-4×4=4.
33.(6分)先化简,再求值:(x-2y)(x+2y)-(2x-y)2+(x+2y)2,其中,x=-1,y=-2.
解
(x-2y)(x+2y)-(2x-y)2+(x+2y)2=x2-4y2-(4x2-4xy+y2)+(x2+4xy+4y2)
=x2-4y2-4x2+4xy-y2+x2+4xy+4y2=-2x2+8xy-y2,
当x=-1,y=-2时,原式=-2×(-1)2+8×(-1)×(-2)-(-2)2=-2+16-4=10.
34.(6分)图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)将图②中的阴影部分面积用两种方法表示可得一个等式,这个等式为 .?
(2)若m+2n=7,mn=3,利用(1)的结论求m-2n的值.
解
(1)(m+n)2-4mn=(m-n)2.故答案为(m+n)2-4mn=(m-n)2.
(2)(m-2n)2=(m+2n)2-8mn=25,则m-2n=±5.
35.(4分)已知(a+b)2=25,(a-b)2=9,求ab与a2+b2的值.
解
∵(a+b)2=25,(a-b)2=9,∴a2+2ab+b2=25①,a2-2ab+b2=9②.∴①+②得2a2+2b2=34.∴a2+b2=17.①-②得4ab=16,∴ab=4.
37.
(4分)已知(x+y)2=1,(x-y)2=49,求x2+y2与xy的值.
解
∵(x+y)2=x2+y2+2xy=1①,(x-y)2=x2+y2-2xy=49②,∴①+②得2(x2+y2)=50,即x2+y2=25;①-②得4xy=-48,即xy=-12.
37.(4分)已知x,y互为相反数,且(x+3)2-(y+3)2=6,求x,y的值.
解
∵x,y互为相反数,∴y=-x.∴(x+3)2-(y+3)2=(x+3)2-(-x+3)2=x2+6x+9-x2+6x-9=6.∴12x=6,解得x=0.5,∴y=-x=-0.5.故x,y的值分别是0.5,-0.5.
38.(8分)如图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状围成一个正方形.
(1)图②中的阴影部分面积为 .?
(2)观察图②,请你写出(m+n)2,(m-n)2,mn之间的等量关系是 .?
(3)实际上有许多恒等式可以用图形的面积来表示,如图③,它表示了 .?
(4)试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.(在图中标出相应的长度)
解
(1)(m+n)2-4mn或(m-n)2;
(2)(m+n)2-4mn=(m-n)2;
(3)(2m+n)(m+n)=2m2+3mn+n2;
(4)如图所示.
乘法公式》强化提优检测(2)
(时间:60分钟
满分:120分)
1.选择题(共20题;共40分)
1.计算(x-5)2=( )
A.x2-25
B.x2+25
C.x2-5x+25
D.x2-10x+25
2.已知2a-3b+4c=2a-( )成立,则括号内应填的项是( )
A.-3b+4c
B.3b-4c
C.-3b-4c
D.3b+4c
3.
应用公式(a+b)(a-b)=a2-b2计算(x+2y-1)(x-2y+1),下列变形正确的是( )
A.[x-(2y+1)]2
B.[x+(2y+1)]2
C.[x-(2y-1)][x+(2y-1)]
D.[(x-2y)+1][(x-2y)-1]
4.已知如图,图中最大的正方形的面积是( )
A.a2
B.a2+b2
C.a2+2ab+b2
D.a2+ab+b2
第4题图
第5题图
5.利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( )
A.(a+b)(a-b)=a2-b2
B.(a-b)2=a2-2ab+b2
C.a(a+b)=a2+ab
D.a(a-b)=a2-ab
6.下列式子中是完全平方式的是( )
A.
a2+ab+b2
B.a2+2a+2
C.a2-2b+b2
D.a2+2a+1
7.已知x2+kxy+64y2是一个完全式,则k的值是( )
A.8
B.±8
C.16
D.±16
8.运用乘法公式计算(x+3)2的结果是( )
A.x2+9
B.x2-6x+9
C.x2+6x+9
D.x2+3x+9
9.计算(2x-1)(1-2x)结果正确的是( )
A.4x2-1
B.1-4x2
C.-4x2+4x-1
D.4x2-4x+1
解析
(2x-1)(1-2x)=-(2x-1)2=-4x2+4x-1,故选C.
10.若a+b=4,ab=2,则a2+b2的值为( )
A.14
B.12
C.10
D.8
解析
把a+b=4两边平方得(a+b)2=a2+b2+2ab=16,把ab=2代入得a2+b2=12,故选B.
11.若9x2+mxy+16y2是一个完全平方式,则m的值为( )
A.24
B.-12
C.±12
D.±24
12.下列多项式中是完全平方式的是( )
A.2x2+4x-4
B.16x2-8y2+1
C.9a2-12a+4
D.x2y2+2xy+y2
13.下列各式中计算正确的是( )
A.(a-b)2=a2-b2
B.(a+2b)2=a2+2ab+4b2
C.(a2+1)2=a4+2a+1
D.(-m-n)2=m2+2mn+n2
14.设(5a+3b)2=(5a-3b)2+A,则A=( )
A.30ab
B.60ab
C.15ab
D.12ab
15、若二次三项式是一个完全平方式,则的值为(??
).
?A.
?B.
C.
?D.
16、填空:___________.---------
(
)
?A.
,
?B.
,
?C.
,
?D.
,
17、在多项式中添加一个单项式,使其成为一个完全平方式,则添加的单项式可以是( )
A.
??B.
???C.
?D.
18.
已知(x-2
019)2+(x-2
021)2=34,则(x-2
020)2的值是( )
A.4
B.8
C.12
D.16
19、已知多项式是一个完全平方式,则的值是(?
)
?A.
14
??B.
-10
??C.
或
??D.
或
20.不论a
b为任何有理数,则a2
+b2
-4a
+2b+7的值总是(
?
).
?A.
负数
??B.
零
??C.
可以为任一正数
??D.
不小于
2.填空题(共10题;共20分)
21.
若(7x-a)2=49x2-bx+9,则|a+b|= .?
22、????????????????????????.
23.若把代数式x2-2x-3化为(x-m)2+k的形式,其中m,k为常数,则m+k=
-3
.
24.若(x+
)2=9,则(x
-
)2的值为
.
25.已知x+y=7且xy=12,则当x<y时,-
的值等于
.
26.若a2+b2=5,ab=2,则(a+b)2=
.
28.已知x+y=1,则x2+xy+y2=
.
29、已知,则的值是????????????.
30、已知,则_________.
3、解答题(共8题;共40分)
31(8分)计算
(1):x(x+1)-(x-1)2.
(2)2x(x-2y)-(2x-y)2
32.(8分)已知x+2y=6,x2+4y2=20,求下列各式的值:
(1)xy;
(2)(x-2y)2.
33.(6分)先化简,再求值:(x-2y)(x+2y)-(2x-y)2+(x+2y)2,其中,x=-1,y=-2.
34.(6分)图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)将图②中的阴影部分面积用两种方法表示可得一个等式,这个等式为 .?
(2)若m+2n=7,mn=3,利用(1)的结论求m-2n的值.
35.
(4分)已知(a+b)2=25,(a-b)2=9,求ab与a2+b2的值.
36.
(4分)已知(x+y)2=1,(x-y)2=49,求x2+y2与xy的值.
37.(4分)已知x,y互为相反数,且(x+3)2-(y+3)2=6,求x,y的值.
38.(8分)如图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状围成一个正方形.
(1)图②中的阴影部分面积为 .?
(2)观察图②,请你写出(m+n)2,(m-n)2,mn之间的等量关系是 .?
(3)实际上有许多恒等式可以用图形的面积来表示,如图③,它表示了 .?
(4)试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.(在图中标出相应的长度)
教师样卷
一.选择题(共20题;共40分)
1.计算(x-5)2=( D )
A.x2-25
B.x2+25
C.x2-5x+25
D.x2-10x+25
2.已知2a-3b+4c=2a-( )成立,则括号内应填的项是( B )
A.-3b+4c
B.3b-4c
C.-3b-4c
D.3b+4c
解析
直接利用添括号法则求出即可,2a-3b+4c=2a-(3b-4c).故选B.
4.
应用公式(a+b)(a-b)=a2-b2计算(x+2y-1)(x-2y+1),下列变形正确的是( C )
A.[x-(2y+1)]2
B.[x+(2y+1)]2
C.[x-(2y-1)][x+(2y-1)]
D.[(x-2y)+1][(x-2y)-1]
解析
(x+2y-1)(x-2y+1)=[x-(2y-1)]·[x+(2y-1)].故选C.
4.已知如图,图中最大的正方形的面积是( C )
A.a2
B.a2+b2
C.a2+2ab+b2
D.a2+ab+b2
第4题图
第5题图
5.利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是( B )
A.(a+b)(a-b)=a2-b2
B.(a-b)2=a2-2ab+b2
C.a(a+b)=a2+ab
D.a(a-b)=a2-ab
6.下列式子中是完全平方式的是( D )
A.
a2+ab+b2
B.a2+2a+2
C.a2-2b+b2
D.a2+2a+1
7.已知x2+kxy+64y2是一个完全式,则k的值是( D )
A.8
B.±8
C.16
D.±16
8.运用乘法公式计算(x+3)2的结果是( C )
A.x2+9
B.x2-6x+9
C.x2+6x+9
D.x2+3x+9
9.计算(2x-1)(1-2x)结果正确的是( C )
A.4x2-1
B.1-4x2
C.-4x2+4x-1
D.4x2-4x+1
解析
(2x-1)(1-2x)=-(2x-1)2=-4x2+4x-1,故选C.
10.若a+b=4,ab=2,则a2+b2的值为( B )
A.14
B.12
C.10
D.8
解析
把a+b=4两边平方得(a+b)2=a2+b2+2ab=16,把ab=2代入得a2+b2=12,故选B.
11.若9x2+mxy+16y2是一个完全平方式,则m的值为( D )
A.24
B.-12
C.±12
D.±24
12.下列多项式中是完全平方式的是( C )
A.2x2+4x-4
B.16x2-8y2+1
C.9a2-12a+4
D.x2y2+2xy+y2
13.下列各式中计算正确的是( D )
A.(a-b)2=a2-b2
B.(a+2b)2=a2+2ab+4b2
C.(a2+1)2=a4+2a+1
D.(-m-n)2=m2+2mn+n2
解析
选项A,应为(a-b)2=a2-2ab+b2,故本选项错误;选项B,应为(a+2b)2=a2+4ab+4b2,故本选项错误;选项C,应为(a2+1)2=a4+2a2+1,故本选项错误;选项D,(-m-n)2=m2+2mn+n2,正确.故选D.
14.设(5a+3b)2=(5a-3b)2+A,则A=( B )
A.30ab
B.60ab
C.15ab
D.12ab
解析
∵(5a+3b)2=(5a-3b)2+A,∴A=(5a+3b)2-(5a-3b)2=(5a+3b+5a-3b)(5a+3b-5a+3b)=60ab.故选B.
15、若二次三项式是一个完全平方式,则的值为(??C?
).
?A.
?B.
C.
?D.
解:
又是一个完全平方式,,.故答案选:.
16、填空:___________.---------
(
A
)
?A.
,
?B.
,
?C.
,
?D.
,
解:,.
故答案应选:,.
17、在多项式中添加一个单项式,使其成为一个完全平方式,则添加的单项式可以是( C )
A.
??B.
???C.
?D.
【解析】①若为平方项,则加上的项是:;②若为乘积二倍项,
则加上的项是:;③若加上后是单项式的平方,则加上的项是:或.
故为:或或或或.
19.
已知(x-2
019)2+(x-2
021)2=34,则(x-2
020)2的值是( B )
A.4
B.8
C.12
D.16
解析
∵(x-2
019)2+(x-2
021)2=34,∴(x-2
020+1)2+(x-2
020-1)2=34.
∴(x-2
020)2+2(x-2
020)+1+(x-2
020)2-2(x-2
020)+1=34.∴2(x-2
020)2+2=34.∴2(x-2
020)2=32.∴(x-2
020)2=16.故选D.
19、已知多项式是一个完全平方式,则的值是(?
C
)
?A.
14
??B.
-10
??C.
或
??D.
或
20.不论a
b为任何有理数,则a2
+b2
-4a
+2b+7的值总是(
D?
).
?A.
负数
??B.
零
??C.
可以为任一正数
??D.
不小于
3.填空题(共10题;共20分)
22.
若(7x-a)2=49x2-bx+9,则|a+b|= .?
【答案】.45 解析
∵(7x-a)2=49x2-bx+9,∴49x2-14ax+a2=49x2-bx+9.∴-14a=-b,a2=9.解得a=3,b=42或a=-3,b=-42.当a=3,b=42时,|a+b|=|3+42|=45;当a=-3,b=-42时,|a+b|=|-3-42|=45.故答案为45.
22、????????????????????????.
【答案】,.
【解析】,
故答案是:,.
23.若把代数式x2-2x-3化为(x-m)2+k的形式,其中m,k为常数,则m+k=
-3
.
【答案】-3
解
:
根据完全平方公式的结构,按照要求x2-2x-3=x2-2x+1-4=(x-1)2-4,可知m=1.k=-4,则m+k=-3.∵x2-2x-3=x2-2x+1-4=(x-1)2-4,∴m=1,k=
-4,∴m+k=-3.故填-3.
24.若(x+
)2=9,则(x
-
)2的值为
.
【答案】5
25.已知x+y=7且xy=12,则当x<y时,-
的值等于
.
【答案】
解:
先运用完全平方公式的变形求出y-x的值,然后代入通分后的所求式子中,计算即可.∵x+y=7且xy=12,∴(x-y)2=(x+y)2-4xy=72-4×12=49-48=1,
∵x<y,∴y-x=1,
∴-
==.
26.若a2+b2=5,ab=2,则(a+b)2=
.
【答案】9
28.已知x+y=1,则x2+xy+y2=
.
【答案】
29、已知,则的值是????????????.
【答案】28
【解析】:,
故答案为:
30、已知,则_________.
【答案】
【解析】:原式可化为,即;∴,,即,.
因此,,.故答案为:.
4、解答题(共8题;共40分)
31.(8分)计算
(1):x(x+1)-(x-1)2.
(2)2x(x-2y)-(2x-y)2
解(1)
x(x+1)-(x-1)2=x2+x-x2+2x-1=3x-1.
(2)2x(x-2y)-(2x-y)2=2x2-4xy-(4x2-4xy+y2)=2x2-4xy-4x2+4xy-y2=-2x2-y2.
32.(8分)已知x+2y=6,x2+4y2=20,求下列各式的值:
(1)xy;
(2)(x-2y)2.
解
(1)∵x+2y=6,∴(x+2y)2=62.∴x2+4xy+4y2=36.∵x2+4y2=20,∴4xy=16.∴xy=4.
(2)∵x2+4y2=20,xy=4,∴(x-2y)2=x2-4xy+4y2=20-4×4=4.
33.(6分)先化简,再求值:(x-2y)(x+2y)-(2x-y)2+(x+2y)2,其中,x=-1,y=-2.
解
(x-2y)(x+2y)-(2x-y)2+(x+2y)2=x2-4y2-(4x2-4xy+y2)+(x2+4xy+4y2)
=x2-4y2-4x2+4xy-y2+x2+4xy+4y2=-2x2+8xy-y2,
当x=-1,y=-2时,原式=-2×(-1)2+8×(-1)×(-2)-(-2)2=-2+16-4=10.
34.(6分)图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)将图②中的阴影部分面积用两种方法表示可得一个等式,这个等式为 .?
(2)若m+2n=7,mn=3,利用(1)的结论求m-2n的值.
解
(1)(m+n)2-4mn=(m-n)2.故答案为(m+n)2-4mn=(m-n)2.
(2)(m-2n)2=(m+2n)2-8mn=25,则m-2n=±5.
35.(4分)已知(a+b)2=25,(a-b)2=9,求ab与a2+b2的值.
解
∵(a+b)2=25,(a-b)2=9,∴a2+2ab+b2=25①,a2-2ab+b2=9②.∴①+②得2a2+2b2=34.∴a2+b2=17.①-②得4ab=16,∴ab=4.
37.
(4分)已知(x+y)2=1,(x-y)2=49,求x2+y2与xy的值.
解
∵(x+y)2=x2+y2+2xy=1①,(x-y)2=x2+y2-2xy=49②,∴①+②得2(x2+y2)=50,即x2+y2=25;①-②得4xy=-48,即xy=-12.
37.(4分)已知x,y互为相反数,且(x+3)2-(y+3)2=6,求x,y的值.
解
∵x,y互为相反数,∴y=-x.∴(x+3)2-(y+3)2=(x+3)2-(-x+3)2=x2+6x+9-x2+6x-9=6.∴12x=6,解得x=0.5,∴y=-x=-0.5.故x,y的值分别是0.5,-0.5.
38.(8分)如图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状围成一个正方形.
(1)图②中的阴影部分面积为 .?
(2)观察图②,请你写出(m+n)2,(m-n)2,mn之间的等量关系是 .?
(3)实际上有许多恒等式可以用图形的面积来表示,如图③,它表示了 .?
(4)试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.(在图中标出相应的长度)
解
(1)(m+n)2-4mn或(m-n)2;
(2)(m+n)2-4mn=(m-n)2;
(3)(2m+n)(m+n)=2m2+3mn+n2;
(4)如图所示.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
