2020-2021学年七年级数学苏科版下册-9.5 多项式的因式分解(1) (1)(共18张ppt)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册-9.5 多项式的因式分解(1) (1)(共18张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 07:52:36 | ||
图片预览






文档简介
(共18张PPT)
9.5多项式的因式分解(1)
提公因式法
计算:
375×2+375×5+375×3
情境引入
375×2+375×5+375×3
=375×(2+5+3)
依据是什么?
乘法分配律
你能把多项式ab+ac+ad写成积的形式吗?
ab+ac+ad=a(b+c+d)
375×2+375×5+375×3
ab+ac+ad
单项式乘多项式的法则a(b+c+d)=ab+ac+ad
1、计算下列各式:
x(x+1)=
;
(x+1)(x-2)=
整式乘法
x2
+
x
2、把下列多项式写成整式乘积的形式:
像这样,
叫做多项式的因式分解
.
x2
+
x=
想一想:因式分解与整式乘法有何关系?
因式分解与整式乘法是互逆过程.
x2-x-2.
x2-x-2=
把一个多项式写成几个整式的积的形式,
反过来
因式分解
ab+ac+ad
多项式
a(b+c+d)整式的积
因式分解
整式乘法
判断下列各式从左到右的变形,是否为因式分解?
(1)
x2-(2y)2=(x+2y)(x-2y);
(2)
2x(x-3y)=2x2-6xy
(3)2πR+
2πr=
2π(R+r)
(4)
x2+4x+4=x(x+4)+4;
(5)2a3b=a2?2ab
√
×
√
×
提示:判定一个变形是因式分解的条件:(1)左边是多项式.(2)右边是积的形式.
(3)右边的因式全是整式.
×
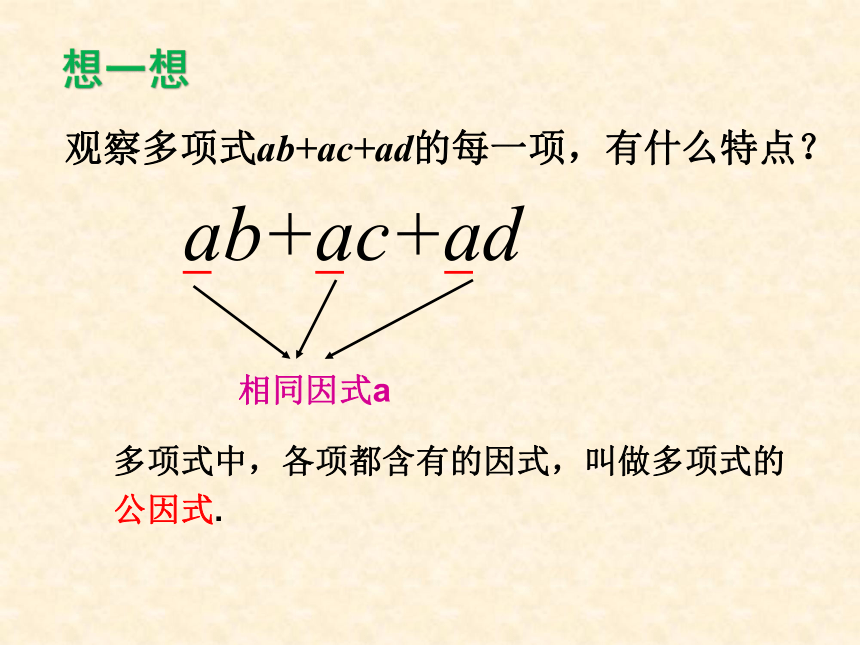
相同因式a
多项式中,各项都含有的因式,叫做多项式的公因式.
观察多项式ab+ac+ad的每一项,有什么特点?
ab+ac+ad
想一想
①
②
③
④
试一试
指出下列各多项式中的公因式:
多项式中的公因式是如何确定的?
找出
的公因式
3
x
1
①定系数:最大公约数
②定字母:相同的字母
③定指数:相同字母的最低次幂
所以,公因式是:
3x
练一练
试一试
因式分解:
把多项式化成公因式与另一个多项式的积的形式,这种分解因式的方法叫做提公因式法.
①确定公因式
②写成公因式×另一因式的形式
③提出公因式
练一练
把下列各式分解因式
解:
←不能漏掉
当多项式的第一项系数为负数时,通常把“—”号作为公因式的符号。
解:
(1)原式=
a(m-6)+b(m-6)
例题
把下列各式进行因式分解:
(1)
a(m-6)+b(m-6)
(2)
3(a-b)+a(b-a)
=(m-6)(a+b)
解:
(2)
原式=3(a-b)+a(b-a)
=3(a-b)-a(a-b)
=(a-b)(3-a)
注意:公因式既可以是一个单项式的形式,
也可以是一个多项式的形式。
=3(a-b)+a[-(a-b)]
练一练:把下列各式分解因式
拓展延伸
——
故能被7整除.
——
谈谈今天的收获
特点:乘积形式
1、因式分解
2、公因式
确定公因式的方法:
1)定系数
2)定字母
3)定指数
3、提公因式法
把多项式写成公因式与另一个多项式的积的形式
注:用提公因式法分解因式应注意的问题:
(1)小心漏项(如:1);
(2)公因式可以是多项式形式.
——
完成《课课练》P55
例2
测一测
后记
1、铺垫太多。公开课的时候多给学生说的机会,然后帮他们提炼、总结。学生可以题前谈发现,也可以题后谈经验。每题结束适当总结。
2、语言应该提前再顺得更精简一些。PPT宜精简。做备选题,以便上课时随机应变,增加变式的练习。
3、对于本节课而言,应增加两题公因式为多项式的因式分解练习,减去一题拓展延伸,减去测一测。
4、放慢速度,把握住重点。
9.5多项式的因式分解(1)
提公因式法
计算:
375×2+375×5+375×3
情境引入
375×2+375×5+375×3
=375×(2+5+3)
依据是什么?
乘法分配律
你能把多项式ab+ac+ad写成积的形式吗?
ab+ac+ad=a(b+c+d)
375×2+375×5+375×3
ab+ac+ad
单项式乘多项式的法则a(b+c+d)=ab+ac+ad
1、计算下列各式:
x(x+1)=
;
(x+1)(x-2)=
整式乘法
x2
+
x
2、把下列多项式写成整式乘积的形式:
像这样,
叫做多项式的因式分解
.
x2
+
x=
想一想:因式分解与整式乘法有何关系?
因式分解与整式乘法是互逆过程.
x2-x-2.
x2-x-2=
把一个多项式写成几个整式的积的形式,
反过来
因式分解
ab+ac+ad
多项式
a(b+c+d)整式的积
因式分解
整式乘法
判断下列各式从左到右的变形,是否为因式分解?
(1)
x2-(2y)2=(x+2y)(x-2y);
(2)
2x(x-3y)=2x2-6xy
(3)2πR+
2πr=
2π(R+r)
(4)
x2+4x+4=x(x+4)+4;
(5)2a3b=a2?2ab
√
×
√
×
提示:判定一个变形是因式分解的条件:(1)左边是多项式.(2)右边是积的形式.
(3)右边的因式全是整式.
×
相同因式a
多项式中,各项都含有的因式,叫做多项式的公因式.
观察多项式ab+ac+ad的每一项,有什么特点?
ab+ac+ad
想一想
①
②
③
④
试一试
指出下列各多项式中的公因式:
多项式中的公因式是如何确定的?
找出
的公因式
3
x
1
①定系数:最大公约数
②定字母:相同的字母
③定指数:相同字母的最低次幂
所以,公因式是:
3x
练一练
试一试
因式分解:
把多项式化成公因式与另一个多项式的积的形式,这种分解因式的方法叫做提公因式法.
①确定公因式
②写成公因式×另一因式的形式
③提出公因式
练一练
把下列各式分解因式
解:
←不能漏掉
当多项式的第一项系数为负数时,通常把“—”号作为公因式的符号。
解:
(1)原式=
a(m-6)+b(m-6)
例题
把下列各式进行因式分解:
(1)
a(m-6)+b(m-6)
(2)
3(a-b)+a(b-a)
=(m-6)(a+b)
解:
(2)
原式=3(a-b)+a(b-a)
=3(a-b)-a(a-b)
=(a-b)(3-a)
注意:公因式既可以是一个单项式的形式,
也可以是一个多项式的形式。
=3(a-b)+a[-(a-b)]
练一练:把下列各式分解因式
拓展延伸
——
故能被7整除.
——
谈谈今天的收获
特点:乘积形式
1、因式分解
2、公因式
确定公因式的方法:
1)定系数
2)定字母
3)定指数
3、提公因式法
把多项式写成公因式与另一个多项式的积的形式
注:用提公因式法分解因式应注意的问题:
(1)小心漏项(如:1);
(2)公因式可以是多项式形式.
——
完成《课课练》P55
例2
测一测
后记
1、铺垫太多。公开课的时候多给学生说的机会,然后帮他们提炼、总结。学生可以题前谈发现,也可以题后谈经验。每题结束适当总结。
2、语言应该提前再顺得更精简一些。PPT宜精简。做备选题,以便上课时随机应变,增加变式的练习。
3、对于本节课而言,应增加两题公因式为多项式的因式分解练习,减去一题拓展延伸,减去测一测。
4、放慢速度,把握住重点。
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
