6.3.2平面向量的正交分解及坐标表示-6.3.3平面向量加、减运算的坐标表示 课件(共40张PPT)2020-2021学年高一下学期人教A版(2019)必修第二册
文档属性
| 名称 | 6.3.2平面向量的正交分解及坐标表示-6.3.3平面向量加、减运算的坐标表示 课件(共40张PPT)2020-2021学年高一下学期人教A版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 00:00:00 | ||
图片预览










文档简介
6.3 平面向量基本定理及坐标表示
6.3.2 平面向量的正交分解及坐标表示
6.3.3 平面向量加、减运算的坐标表示
课标定位
素养阐释
1.借助平面直角坐标系,掌握平面向量的正交分解及坐标表示.
2.会用坐标表示平面向量的加、减运算.
3.培养直观想象、数学抽象和数学运算素养.
自主预习·新知导学
合作探究·释疑解惑
易 错 辨 析
随 堂 练 习
自主预习·新知导学
一、平面向量的坐标表示
【问题思考】
1.如图,向量i,j是两个互相垂直的单位向量,向量a与i的夹角是30°,且|a|=4,以向量i,j为基底,向量a如何表示?
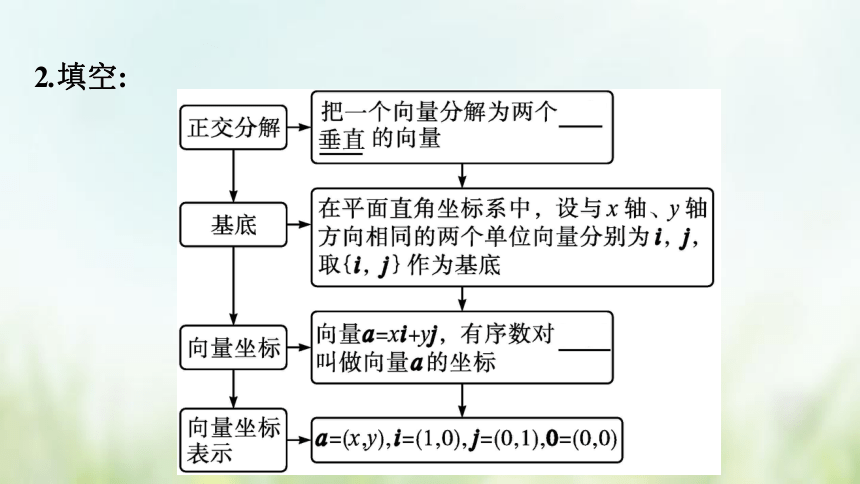
2.填空:
3.做一做:在平面直角坐标系中,若i,j是与x轴、y轴正方向相同的单位向量,且a=2i-6j,b=5j,c=-4i,则向量a,b,c的坐标分别是 , , .?
答案:(2,-6) (0,5) (-4,0)
二、平面向量加、减运算的坐标表示
【问题思考】
1.设i,j是与x轴、y轴同向的两个单位向量,若a=(x1,y1), b=(x2,y2),则a=x1i+y1j,b=x2i+y2j,根据向量的线性运算性质,向量a+b,a-b如何分别用基底i,j表示?
提示:a+b=(x1+x2)i+(y1+y2)j,a-b=(x1-x2)i+(y1-y2)j.
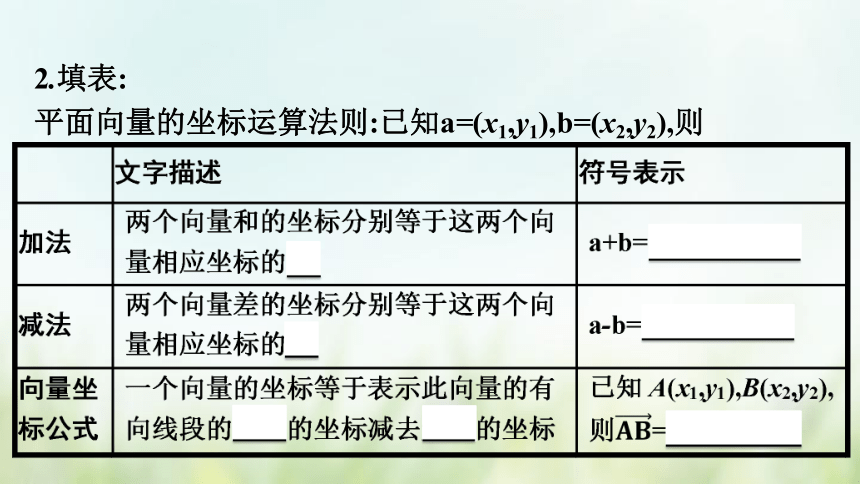
2.填表:
平面向量的坐标运算法则:已知a=(x1,y1),b=(x2,y2),则
3.做一做:(1)若a=(3,-2),b=(-1,4),则a+b= ,
a-b= . ?
答案:(1)(2,2) (4,-6) (2)(2,10) (-2,-10)
【思考辨析】
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)相等的向量,其坐标是相同的.( √ )
(2)一个向量平移后其坐标也发生了变化.( × )
(3)一个向量的坐标等于其起点的坐标减去其终点的坐标.
( × )
(4)若a=(1,-2),则必有a=i-2j,其中i,j是与x轴、y轴正方向相同的单位向量.( √ )
合作探究·释疑解惑
探究一
探究二
探究三
探究一 向量的坐标表示
分析:(1)利用平行四边形法则表示向量;(2)先求出点A,B,C,D的坐标,再根据点的坐标与向量坐标的关系求出向量坐标.
求平面向量坐标的方法:
(1)若i,j是分别与x轴、y轴同方向的单位向量,则当a=xi+yj时,向量a的坐标即为(x,y).
(2)向量的坐标等于其终点的相应坐标减去始点的相应坐标,只有当向量的始点在坐标原点时,向量的坐标才等于终点的坐标.
(3)求向量的坐标一般转化为求点的坐标.解题时,常常结合几何图形,利用三角函数的定义和性质进行计算.
探究二 向量加、减运算的坐标表示
【例2】 (1)设向量a,b的坐标分别是(-1,2),(3,-5),则a+b= ,b-a= .?
解析:a+b=(-1,2)+(3,-5)=(-1+3,2-5)=(2,-3);
b-a=(3,-5)-(-1,2)=(3+1,-5-2)=(4,-7).
答案:(2,-3) (4,-7)
向量加、减运算的坐标表示要注意的问题
(1)向量加、减运算的坐标表示主要是利用加法、减法运算法则进行,若已知有向线段两端点的坐标,则应先求出向量的坐标,要注意三角形法则及平行四边形法则的应用.
(2)若是给出向量的坐标,解题过程中要注意方程思想的运用及正确使用运算法则.
答案:A
探究三 向量加、减坐标运算的应用
平面向量加、减坐标运算应用技巧:
(1)用待定系数法,此法是最基本的数学方法之一,将未知量设出来,建立方程(组)求出未知数的值,是待定系数法的基本形式,也是方程思想的一种基本应用.
(2)坐标形式下向量相等的条件:相等向量的对应坐标相等;对应坐标相等的向量是相等向量.由此可建立相等关系求某些参数的值.
易 错 辨 析
分类讨论不全面致误
【典例】 已知A(3,2),B(5,4),C(6,7),求以A,B,C为顶点的平行四边形的另一个顶点D的坐标.
可得(5-3,4-2)=(6-x,7-y),解得x=4,y=5.
故所求顶点D的坐标为(4,5).
以上解答过程中都有哪些错误?出错的原因是什么?你如何改正?你如何防范?
提示:错解只考虑了平行四边形ABCD这一种情况,漏掉了其他平行四边形的情况.平行四边形四个顶点按逆时针顺序排列有三种可能,即ABCD,ABDC,ADBC.还有另外两种情况没有考虑.
故所求顶点D的坐标为(2,-1).
综上可得,以A,B,C为顶点的平行四边形的另一个顶点D的坐标是(4,5)或(8,9)或(2,-1).
“求以A,B,C为顶点的平行四边形ABCD的第四个顶点的坐标”与“求以A,B,C为顶点的平行四边形的另一个顶点的坐标”是有区别的.前者的点D位置确定了,四点A,B,C,D是按同一方向(顺时针或逆时针)排列,后者的点D位置没有确定,应分三种情况进行讨论.
【变式训练】 已知一个平行四边形的三个顶点的坐标分别是(5,7),(-3,5),(3,4),则第四个顶点的坐标不可能是( )
A.(-1,8) B.(-5,2) C.(11,6) D.(5,2)
综上所述,点D坐标为(11,6)或(-5,2)或(-1,8),所以不可能是(5,2).
答案:D
随 堂 练 习
1.向量正交分解中,两基底的夹角等于( )
A.45° B.90°
C.180° D.不确定
答案:B
答案:C
3.已知向量 (O为原点)的终点A位于第二象限,则有
( )
A.x>0,y>0 B.x>0,y<0
C.x<0,y>0 D.x<0,y<0
答案:C
答案:-1 -2
答案:(-3,-5)
6.3.2 平面向量的正交分解及坐标表示
6.3.3 平面向量加、减运算的坐标表示
课标定位
素养阐释
1.借助平面直角坐标系,掌握平面向量的正交分解及坐标表示.
2.会用坐标表示平面向量的加、减运算.
3.培养直观想象、数学抽象和数学运算素养.
自主预习·新知导学
合作探究·释疑解惑
易 错 辨 析
随 堂 练 习
自主预习·新知导学
一、平面向量的坐标表示
【问题思考】
1.如图,向量i,j是两个互相垂直的单位向量,向量a与i的夹角是30°,且|a|=4,以向量i,j为基底,向量a如何表示?
2.填空:
3.做一做:在平面直角坐标系中,若i,j是与x轴、y轴正方向相同的单位向量,且a=2i-6j,b=5j,c=-4i,则向量a,b,c的坐标分别是 , , .?
答案:(2,-6) (0,5) (-4,0)
二、平面向量加、减运算的坐标表示
【问题思考】
1.设i,j是与x轴、y轴同向的两个单位向量,若a=(x1,y1), b=(x2,y2),则a=x1i+y1j,b=x2i+y2j,根据向量的线性运算性质,向量a+b,a-b如何分别用基底i,j表示?
提示:a+b=(x1+x2)i+(y1+y2)j,a-b=(x1-x2)i+(y1-y2)j.
2.填表:
平面向量的坐标运算法则:已知a=(x1,y1),b=(x2,y2),则
3.做一做:(1)若a=(3,-2),b=(-1,4),则a+b= ,
a-b= . ?
答案:(1)(2,2) (4,-6) (2)(2,10) (-2,-10)
【思考辨析】
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.
(1)相等的向量,其坐标是相同的.( √ )
(2)一个向量平移后其坐标也发生了变化.( × )
(3)一个向量的坐标等于其起点的坐标减去其终点的坐标.
( × )
(4)若a=(1,-2),则必有a=i-2j,其中i,j是与x轴、y轴正方向相同的单位向量.( √ )
合作探究·释疑解惑
探究一
探究二
探究三
探究一 向量的坐标表示
分析:(1)利用平行四边形法则表示向量;(2)先求出点A,B,C,D的坐标,再根据点的坐标与向量坐标的关系求出向量坐标.
求平面向量坐标的方法:
(1)若i,j是分别与x轴、y轴同方向的单位向量,则当a=xi+yj时,向量a的坐标即为(x,y).
(2)向量的坐标等于其终点的相应坐标减去始点的相应坐标,只有当向量的始点在坐标原点时,向量的坐标才等于终点的坐标.
(3)求向量的坐标一般转化为求点的坐标.解题时,常常结合几何图形,利用三角函数的定义和性质进行计算.
探究二 向量加、减运算的坐标表示
【例2】 (1)设向量a,b的坐标分别是(-1,2),(3,-5),则a+b= ,b-a= .?
解析:a+b=(-1,2)+(3,-5)=(-1+3,2-5)=(2,-3);
b-a=(3,-5)-(-1,2)=(3+1,-5-2)=(4,-7).
答案:(2,-3) (4,-7)
向量加、减运算的坐标表示要注意的问题
(1)向量加、减运算的坐标表示主要是利用加法、减法运算法则进行,若已知有向线段两端点的坐标,则应先求出向量的坐标,要注意三角形法则及平行四边形法则的应用.
(2)若是给出向量的坐标,解题过程中要注意方程思想的运用及正确使用运算法则.
答案:A
探究三 向量加、减坐标运算的应用
平面向量加、减坐标运算应用技巧:
(1)用待定系数法,此法是最基本的数学方法之一,将未知量设出来,建立方程(组)求出未知数的值,是待定系数法的基本形式,也是方程思想的一种基本应用.
(2)坐标形式下向量相等的条件:相等向量的对应坐标相等;对应坐标相等的向量是相等向量.由此可建立相等关系求某些参数的值.
易 错 辨 析
分类讨论不全面致误
【典例】 已知A(3,2),B(5,4),C(6,7),求以A,B,C为顶点的平行四边形的另一个顶点D的坐标.
可得(5-3,4-2)=(6-x,7-y),解得x=4,y=5.
故所求顶点D的坐标为(4,5).
以上解答过程中都有哪些错误?出错的原因是什么?你如何改正?你如何防范?
提示:错解只考虑了平行四边形ABCD这一种情况,漏掉了其他平行四边形的情况.平行四边形四个顶点按逆时针顺序排列有三种可能,即ABCD,ABDC,ADBC.还有另外两种情况没有考虑.
故所求顶点D的坐标为(2,-1).
综上可得,以A,B,C为顶点的平行四边形的另一个顶点D的坐标是(4,5)或(8,9)或(2,-1).
“求以A,B,C为顶点的平行四边形ABCD的第四个顶点的坐标”与“求以A,B,C为顶点的平行四边形的另一个顶点的坐标”是有区别的.前者的点D位置确定了,四点A,B,C,D是按同一方向(顺时针或逆时针)排列,后者的点D位置没有确定,应分三种情况进行讨论.
【变式训练】 已知一个平行四边形的三个顶点的坐标分别是(5,7),(-3,5),(3,4),则第四个顶点的坐标不可能是( )
A.(-1,8) B.(-5,2) C.(11,6) D.(5,2)
综上所述,点D坐标为(11,6)或(-5,2)或(-1,8),所以不可能是(5,2).
答案:D
随 堂 练 习
1.向量正交分解中,两基底的夹角等于( )
A.45° B.90°
C.180° D.不确定
答案:B
答案:C
3.已知向量 (O为原点)的终点A位于第二象限,则有
( )
A.x>0,y>0 B.x>0,y<0
C.x<0,y>0 D.x<0,y<0
答案:C
答案:-1 -2
答案:(-3,-5)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
