人教版八年级下册数学利用勾股定理解决折叠问题课件(共22张ppt)
文档属性
| 名称 | 人教版八年级下册数学利用勾股定理解决折叠问题课件(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 528.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 00:00:00 | ||
图片预览





文档简介
利用勾股定理解决折叠问题
1. 掌握勾股定理,能够熟练地运用勾股定理求直角三角形的边长;
2. 能够运用勾股定理及方程思想解决简单的折叠问题。
学习目标
复习巩固
2.在直角三角形中勾股定理的用法?
(1)已知直角三角形的两边长,求第三条边长;
(2)已知直角三角形的一条边长和另外两条边长的关系,可求未知的边长。
1.勾股定理的内容?
复习巩固
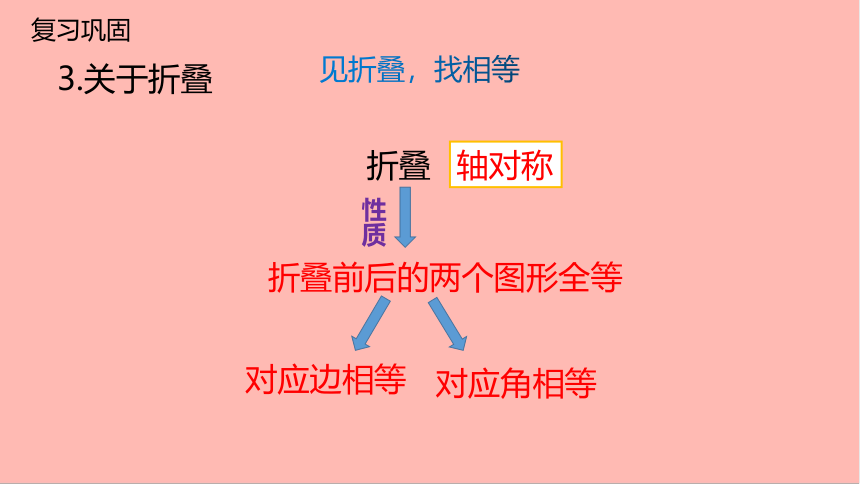
3.关于折叠
轴对称
对应边相等
折叠
性质
折叠前后的两个图形全等
对应角相等
见折叠,找相等
知识点梳理一、勾股定理
勾股定理的定义:直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两直角边长分别为,斜边长为,那么.
勾股定理的含义:勾股定理揭示了一个直角三角形三边之间的数量关系.
勾股定理的应用:利用勾股定理,当设定一条直角边长为未知数后,根据题目已知的线段长可以建立方程求解,这样就将数与形有机地结合起来,达到了解决问题的目的.
勾股定理的一些变式:
知识点梳理二、利用勾股定理解决折叠问题的解题思路 1.总体解题思路:折叠性质+方程思想+勾股定理 2.解题思路步骤:设所求线段为未知数,利用折叠性质,把能用未知数表示的线段表示出,勾股定理所需的直角三角形一般就会呈现在图上,符合这样的直角三角形一般有如下特征:一直角边为具体数字,另一直角边和斜边分别是含有未知数的代数式。 3.注意折叠问题中常出现的数学典型模型:“角平分线+平行线=等腰△”
合作探究
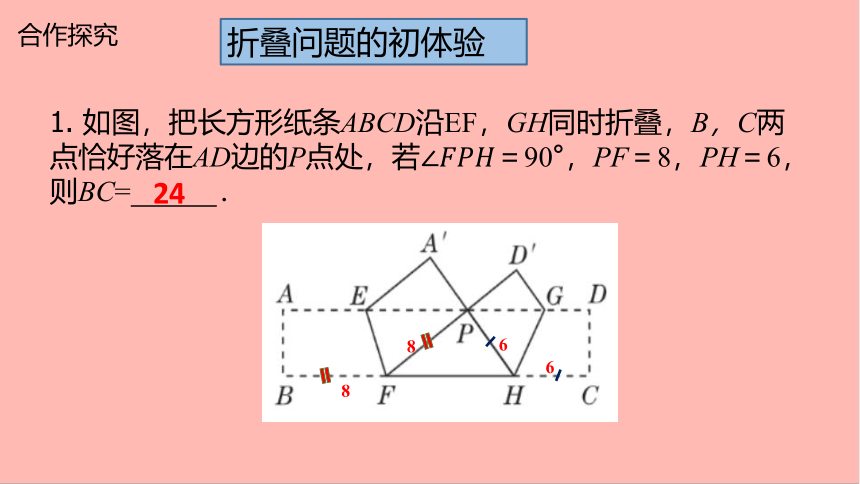
折叠问题的初体验
1. 如图,把长方形纸条ABCD沿EF,GH同时折叠,B,C两点恰好落在AD边的P点处,若∠????????????=90°,PF=8,PH=6,则BC= .
?
8
8
6
6
24
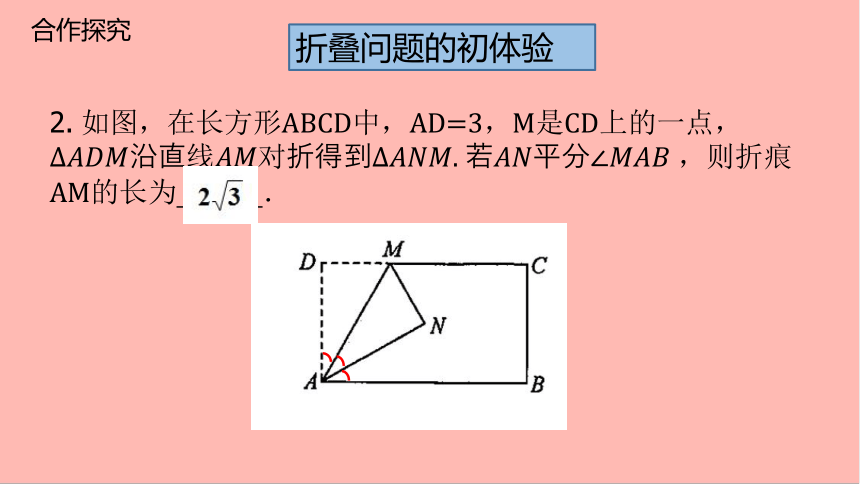
折叠问题的初体验
2. 如图,在长方形ABCD中,AD=3,M是CD上的一点, ?????????????沿直线????????对折得到?????????????. 若????????平分∠???????????? ,则折痕AM的长为 .
?
合作探究
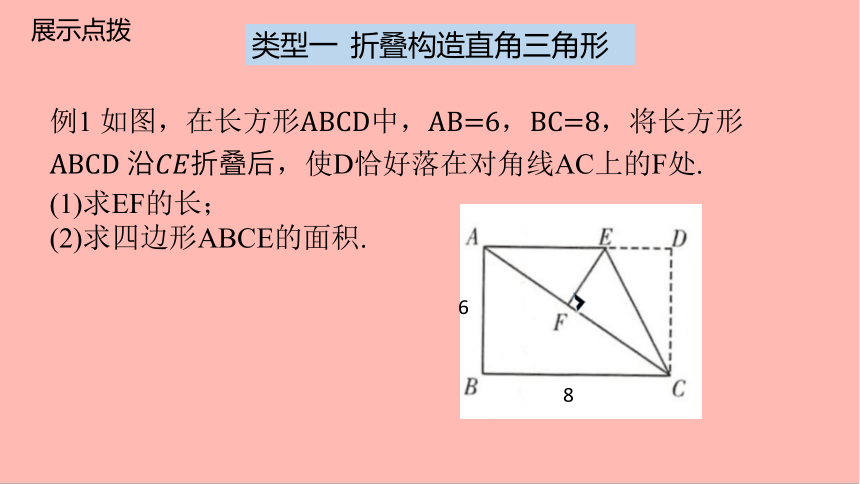
例1 如图,在长方形ABCD中,AB=6,BC=8,将长方形ABCD 沿????????折叠后,使D恰好落在对角线AC上的F处.
(1)求EF的长;
(2)求四边形ABCE的面积.
?
类型一 折叠构造直角三角形
6
8
展示点拨
解:(1)∵四边形????????????????是矩形
∴CD=AB=6,AD=BC=8
∠B=∠D=90°
∵CE为折痕
∴EF=ED CF=CD=6
∠EFC=∠D=90°
∴∠AFE=180°-∠EFC=90°
在Rt?ABC中
AC= AB2+BC2 =10
∴AF=AC-CF=4
设EF=x,则ED=EF=x
AE=AD-ED=8-x
在Rt?AEF中
AF2+EF2=AE2
即42+????2=(8?????)2
解得 x=3
?
跟踪训练1 如图,将等腰直角三角形ABC(∠B=90°)沿EF折叠,使点A落在BC边的中点A1处,BC=8,那么线段AE的长度为 .
展示点拨
类型一 折叠构造直角三角形
类型一 折叠构造直角三角形
【方法技巧】
总体解题思路:
折叠性质+方程思想+勾股定理
解题关键:
确定列方程所需的直角三角形
4
x
8-x
4
x
x
8-x
特征:一直角边为具体数字,另一直角边和斜边分别是含有未知数的代数式。
类型一 折叠构造直角三角形
例2 如图,E为矩形ABCD的边AB上一点, 将矩形沿CE折叠,使点B恰好落在ED上的点F处. 若BE=1,BC=3,则CD的长为 .
类型二 折叠构造全等三角形
跟踪训练 如图,将长方形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDE
(2)若AB=4,BC=8,求图中阴影部分的面积.
类型二 折叠构造全等三角形
数学模型:
平行+角平分线=等腰三角形
如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处. 若AE=3,AB=4,则BF的长为 .
类型三 折叠构造等腰三角形
课堂小结
利用勾股定理解决折叠问题
总体解题思路:
解题关键:
(三大类型题)
折叠性质+方程思想+勾股定理
确定列方程所需的直角三角形
思考的三个层次
直角三角形
全等三角形
等腰三角形
1.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使点A与BC的中点D重合,折痕为MN,则线段BN的长为( )
A.4 B.3 C.2 D.5
A
课堂练习
2.如图,有一块直角三角形纸片,两直角边AC=6,BC=8,现将直角边AC沿直线AD折叠,使AC恰好落在斜边AB上,且点C与点E重合,则CD的长为( )
A.2 B.3 C.4 D.5
B
3.如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点,沿过点E的直线折叠,使点B与点A重合,折痕现交于点F,已知EF=
,则BC的长是( )
B
4.如图是一张直角三角形的纸片,两直角边AC=6 cm、BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4 cm B.5 cm C.6 cm D.10 cm
B
C
1. 掌握勾股定理,能够熟练地运用勾股定理求直角三角形的边长;
2. 能够运用勾股定理及方程思想解决简单的折叠问题。
学习目标
复习巩固
2.在直角三角形中勾股定理的用法?
(1)已知直角三角形的两边长,求第三条边长;
(2)已知直角三角形的一条边长和另外两条边长的关系,可求未知的边长。
1.勾股定理的内容?
复习巩固
3.关于折叠
轴对称
对应边相等
折叠
性质
折叠前后的两个图形全等
对应角相等
见折叠,找相等
知识点梳理一、勾股定理
勾股定理的定义:直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两直角边长分别为,斜边长为,那么.
勾股定理的含义:勾股定理揭示了一个直角三角形三边之间的数量关系.
勾股定理的应用:利用勾股定理,当设定一条直角边长为未知数后,根据题目已知的线段长可以建立方程求解,这样就将数与形有机地结合起来,达到了解决问题的目的.
勾股定理的一些变式:
知识点梳理二、利用勾股定理解决折叠问题的解题思路 1.总体解题思路:折叠性质+方程思想+勾股定理 2.解题思路步骤:设所求线段为未知数,利用折叠性质,把能用未知数表示的线段表示出,勾股定理所需的直角三角形一般就会呈现在图上,符合这样的直角三角形一般有如下特征:一直角边为具体数字,另一直角边和斜边分别是含有未知数的代数式。 3.注意折叠问题中常出现的数学典型模型:“角平分线+平行线=等腰△”
合作探究
折叠问题的初体验
1. 如图,把长方形纸条ABCD沿EF,GH同时折叠,B,C两点恰好落在AD边的P点处,若∠????????????=90°,PF=8,PH=6,则BC= .
?
8
8
6
6
24
折叠问题的初体验
2. 如图,在长方形ABCD中,AD=3,M是CD上的一点, ?????????????沿直线????????对折得到?????????????. 若????????平分∠???????????? ,则折痕AM的长为 .
?
合作探究
例1 如图,在长方形ABCD中,AB=6,BC=8,将长方形ABCD 沿????????折叠后,使D恰好落在对角线AC上的F处.
(1)求EF的长;
(2)求四边形ABCE的面积.
?
类型一 折叠构造直角三角形
6
8
展示点拨
解:(1)∵四边形????????????????是矩形
∴CD=AB=6,AD=BC=8
∠B=∠D=90°
∵CE为折痕
∴EF=ED CF=CD=6
∠EFC=∠D=90°
∴∠AFE=180°-∠EFC=90°
在Rt?ABC中
AC= AB2+BC2 =10
∴AF=AC-CF=4
设EF=x,则ED=EF=x
AE=AD-ED=8-x
在Rt?AEF中
AF2+EF2=AE2
即42+????2=(8?????)2
解得 x=3
?
跟踪训练1 如图,将等腰直角三角形ABC(∠B=90°)沿EF折叠,使点A落在BC边的中点A1处,BC=8,那么线段AE的长度为 .
展示点拨
类型一 折叠构造直角三角形
类型一 折叠构造直角三角形
【方法技巧】
总体解题思路:
折叠性质+方程思想+勾股定理
解题关键:
确定列方程所需的直角三角形
4
x
8-x
4
x
x
8-x
特征:一直角边为具体数字,另一直角边和斜边分别是含有未知数的代数式。
类型一 折叠构造直角三角形
例2 如图,E为矩形ABCD的边AB上一点, 将矩形沿CE折叠,使点B恰好落在ED上的点F处. 若BE=1,BC=3,则CD的长为 .
类型二 折叠构造全等三角形
跟踪训练 如图,将长方形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDE
(2)若AB=4,BC=8,求图中阴影部分的面积.
类型二 折叠构造全等三角形
数学模型:
平行+角平分线=等腰三角形
如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处. 若AE=3,AB=4,则BF的长为 .
类型三 折叠构造等腰三角形
课堂小结
利用勾股定理解决折叠问题
总体解题思路:
解题关键:
(三大类型题)
折叠性质+方程思想+勾股定理
确定列方程所需的直角三角形
思考的三个层次
直角三角形
全等三角形
等腰三角形
1.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使点A与BC的中点D重合,折痕为MN,则线段BN的长为( )
A.4 B.3 C.2 D.5
A
课堂练习
2.如图,有一块直角三角形纸片,两直角边AC=6,BC=8,现将直角边AC沿直线AD折叠,使AC恰好落在斜边AB上,且点C与点E重合,则CD的长为( )
A.2 B.3 C.4 D.5
B
3.如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点,沿过点E的直线折叠,使点B与点A重合,折痕现交于点F,已知EF=
,则BC的长是( )
B
4.如图是一张直角三角形的纸片,两直角边AC=6 cm、BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4 cm B.5 cm C.6 cm D.10 cm
B
C
