2020-2021学年人教版八年级下册18.1.1 平行四边形的性质第2课时 平行四边形的对角线的特征课件(共20张ppt)
文档属性
| 名称 | 2020-2021学年人教版八年级下册18.1.1 平行四边形的性质第2课时 平行四边形的对角线的特征课件(共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 10:33:28 | ||
图片预览





文档简介
(共20张PPT)
第十八章 平行四边形
八年级数学下册人教版
18.1 平行四边形
第2课时 平行四边形的对角线的特征
18.1.1 平行四边形的性质
知识点一 平行四边形的对角线互相平分
1.如图,在□ABCD中,对角线AC与BD相交于点O,则下列结论不一定成立的是( )
A.BO=DO
B.CD=AB
C.∠BAD=∠BCD
D.AC=BD
D
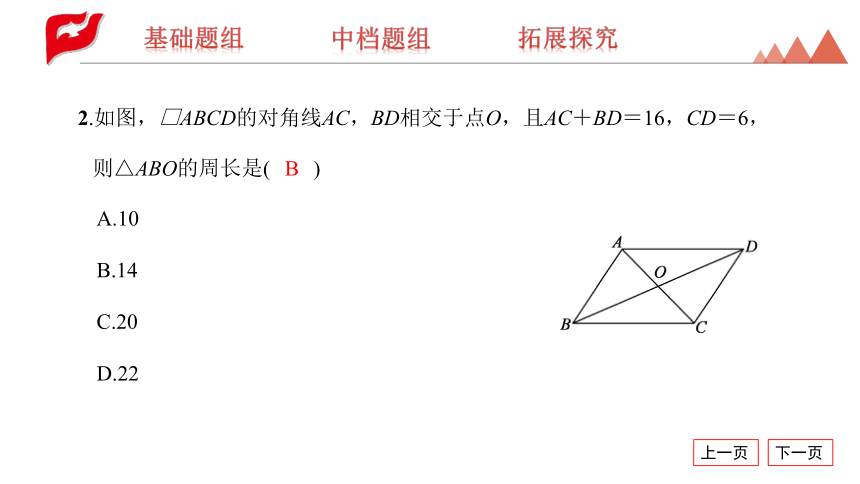
2.如图,□ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10
B.14
C.20
D.22
B
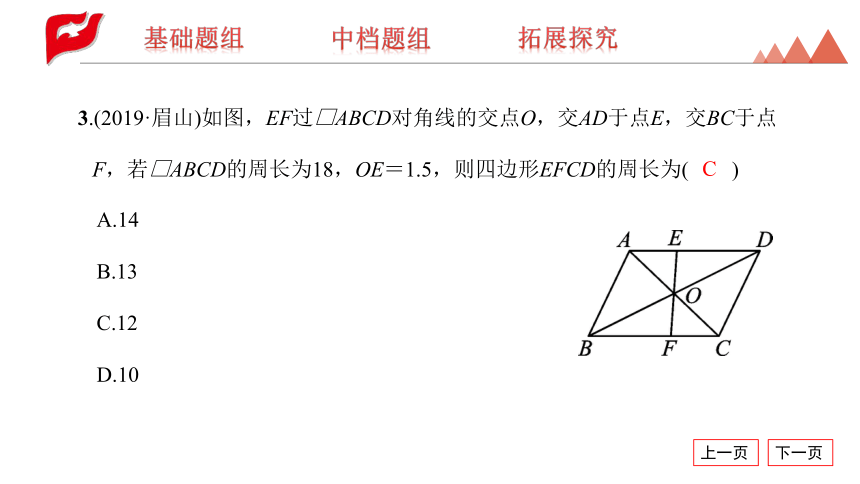
3.(2019·眉山)如图,EF过□ABCD对角线的交点O,交AD于点E,交BC于点F,若□ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( )
A.14
B.13
C.12
D.10
C
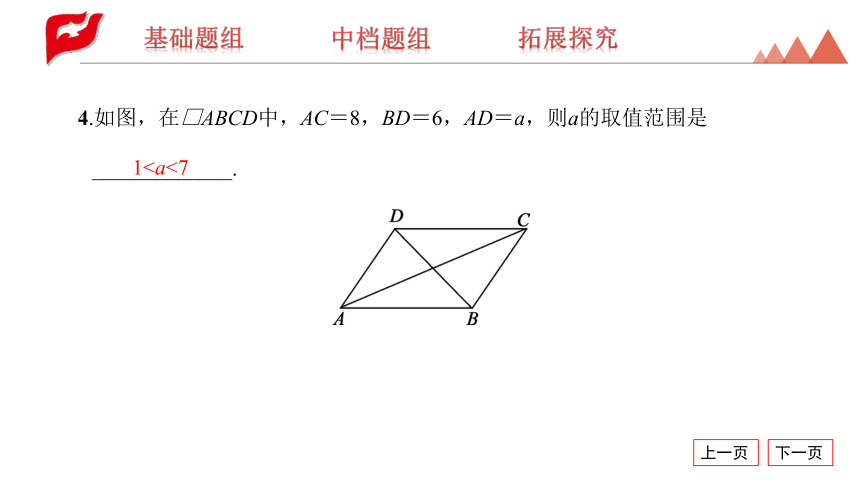
4.如图,在□ABCD中,AC=8,BD=6,AD=a,则a的取值范围是_____________.
15.(课本P44练习T2改编)如图,□ABCD的对角线AC,BD相交于点O,E,F分别是OA,OC的中点.求证:BE=DF.
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,F分别是OA,OC的中点,
在△DOF和△BOE中,
∴△DOF≌△BOE(SAS),∴BE=DF.
知识点二 平行四边形的面积
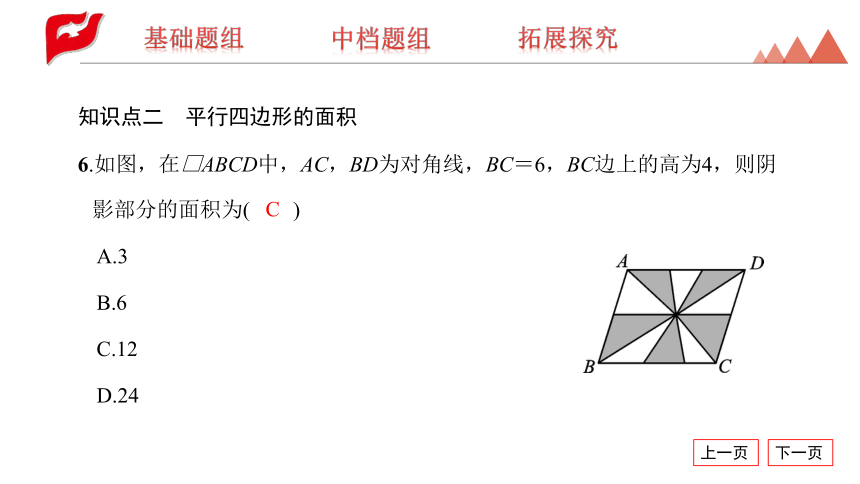
6.如图,在□ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( )
A.3
B.6
C.12
D.24
C
7.设点M是□ABCD边AB上任意一点,△AMD的面积为S1,△BMC的面积为S2,△CDM的面积为S,则S1,S2,S的数量关系为( )
A.S=S1+S2
B.S>S1+S2
C.SD.不能确定
8.□ABCD的对角线AC,BD交于点O,若△AOB的面积为3,则△ABC的面积为________,□ABCD的面积为________.
A
6
12
9.如图,在□ABCD中,对角线AC,BD交于点O,若DO=1.5
cm,AB=5
cm,BC=4
cm,求□ABCD的面积.
解:∵四边形ABCD是平行四边形,
DO=1.5
cm,AB=5
cm,
∴DB=3
cm,CD=AB=5
cm.
又∵BC=4
cm,∴DB2+BC2=CD2,
∴△DBC是直角三角形,且∠CBD=90°,
∴DB⊥BC.∴S□ABCD=BC·DB=3×4=12(cm2).
10.如图,在□ABCD中,AB=4,BC=6,∠B=30°,则此平行四边形的面积是( )
A.6
B.12
C.18
D.24
B
11.(2019·遂宁)如图,在□ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,若□ABCD的周长为28,则△ABE的周长为( )
A.28
B.24
C.21
D.14
D
12.如图,在□ABCD中,对角线AC与BD相交于点O,且AB⊥AC.若AD=5,AB=3,则对角线BD的长为( )
A.
B.
C.9
D.8
B
13.如图,在□ABCD中,AC,BD相交于点O,两条对角线的和为20
cm,△OCD的周长为18
cm,求AB的长.
解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AB=CD,
∴OC=2(1)AC,OD=2(1)BD.
∵AC+BD=20
cm,∴OC+OD=10
cm.
又∵OC+OD+CD=18
cm,
∴CD=8
cm.∴AB=CD=8
cm.
14.(课本P44例2改编)如图,在□ABCD中,AB∶BC=5∶4,对角线AC,BD相交于点O,且BD⊥AD,BD=6.
(1)求AB,BC,AC的值;
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OA=OC,OB=OD.
∵AB∶BC=5∶4,∴设AB=5x,则AD=BC=4x.
在Rt△ABD中,根据勾股定理,得AD2+BD2=AB2,即(4x)2+62=(5x)2,
解得x=2.∴AB=10,BC=AD=8.
在Rt△AOD中,AD2+OD2=OA2,∴82+32=OA2,
解得
(2)求□ABCD的面积.
解:S□ABCD=AD·BD=8×6=48.
15.如图1,□ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC相交于点E,F,则OE=OF.若将EF向两边延长与平行四边形的两组对边的延长线分别相交(如图2,图3),OE与OF还相等吗?若相等,请说明理由.
解:图2中仍然相等.理由如下:∵四边形ABCD为平行四边形,∴AB∥CD,OA=OC,∴∠E=∠F.又∵∠AOE=∠COF,∴△AOE≌△COF(AAS),∴OE=OF.图3中仍然相等.理由如下:∵四边形ABCD为平行四边形,∴AD∥BC,OA=OC,∴∠E=∠F.又∵∠AOE=∠COF,∴△AOE≌COF(AAS),∴OE=OF.
【方法归纳】
如图,在□ABCD中,有以下结论:
(1)△AOD的周长-△AOB的周长=AD-AB(AD>AB);
(2)S△AOB=S△AOD=S△BOC=S△COD=
S□ABCD;
(3)过点O的任意一条直线平分□ABCD的周长和面积;
(4)平行四边形一条对角线的两端点到另一条对角线的距离相等.
第十八章 平行四边形
八年级数学下册人教版
18.1 平行四边形
第2课时 平行四边形的对角线的特征
18.1.1 平行四边形的性质
知识点一 平行四边形的对角线互相平分
1.如图,在□ABCD中,对角线AC与BD相交于点O,则下列结论不一定成立的是( )
A.BO=DO
B.CD=AB
C.∠BAD=∠BCD
D.AC=BD
D
2.如图,□ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10
B.14
C.20
D.22
B
3.(2019·眉山)如图,EF过□ABCD对角线的交点O,交AD于点E,交BC于点F,若□ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( )
A.14
B.13
C.12
D.10
C
4.如图,在□ABCD中,AC=8,BD=6,AD=a,则a的取值范围是_____________.
1
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,F分别是OA,OC的中点,
在△DOF和△BOE中,
∴△DOF≌△BOE(SAS),∴BE=DF.
知识点二 平行四边形的面积
6.如图,在□ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则阴影部分的面积为( )
A.3
B.6
C.12
D.24
C
7.设点M是□ABCD边AB上任意一点,△AMD的面积为S1,△BMC的面积为S2,△CDM的面积为S,则S1,S2,S的数量关系为( )
A.S=S1+S2
B.S>S1+S2
C.S
8.□ABCD的对角线AC,BD交于点O,若△AOB的面积为3,则△ABC的面积为________,□ABCD的面积为________.
A
6
12
9.如图,在□ABCD中,对角线AC,BD交于点O,若DO=1.5
cm,AB=5
cm,BC=4
cm,求□ABCD的面积.
解:∵四边形ABCD是平行四边形,
DO=1.5
cm,AB=5
cm,
∴DB=3
cm,CD=AB=5
cm.
又∵BC=4
cm,∴DB2+BC2=CD2,
∴△DBC是直角三角形,且∠CBD=90°,
∴DB⊥BC.∴S□ABCD=BC·DB=3×4=12(cm2).
10.如图,在□ABCD中,AB=4,BC=6,∠B=30°,则此平行四边形的面积是( )
A.6
B.12
C.18
D.24
B
11.(2019·遂宁)如图,在□ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,若□ABCD的周长为28,则△ABE的周长为( )
A.28
B.24
C.21
D.14
D
12.如图,在□ABCD中,对角线AC与BD相交于点O,且AB⊥AC.若AD=5,AB=3,则对角线BD的长为( )
A.
B.
C.9
D.8
B
13.如图,在□ABCD中,AC,BD相交于点O,两条对角线的和为20
cm,△OCD的周长为18
cm,求AB的长.
解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,AB=CD,
∴OC=2(1)AC,OD=2(1)BD.
∵AC+BD=20
cm,∴OC+OD=10
cm.
又∵OC+OD+CD=18
cm,
∴CD=8
cm.∴AB=CD=8
cm.
14.(课本P44例2改编)如图,在□ABCD中,AB∶BC=5∶4,对角线AC,BD相交于点O,且BD⊥AD,BD=6.
(1)求AB,BC,AC的值;
解:∵四边形ABCD是平行四边形,
∴AB=CD,BC=AD,OA=OC,OB=OD.
∵AB∶BC=5∶4,∴设AB=5x,则AD=BC=4x.
在Rt△ABD中,根据勾股定理,得AD2+BD2=AB2,即(4x)2+62=(5x)2,
解得x=2.∴AB=10,BC=AD=8.
在Rt△AOD中,AD2+OD2=OA2,∴82+32=OA2,
解得
(2)求□ABCD的面积.
解:S□ABCD=AD·BD=8×6=48.
15.如图1,□ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC相交于点E,F,则OE=OF.若将EF向两边延长与平行四边形的两组对边的延长线分别相交(如图2,图3),OE与OF还相等吗?若相等,请说明理由.
解:图2中仍然相等.理由如下:∵四边形ABCD为平行四边形,∴AB∥CD,OA=OC,∴∠E=∠F.又∵∠AOE=∠COF,∴△AOE≌△COF(AAS),∴OE=OF.图3中仍然相等.理由如下:∵四边形ABCD为平行四边形,∴AD∥BC,OA=OC,∴∠E=∠F.又∵∠AOE=∠COF,∴△AOE≌COF(AAS),∴OE=OF.
【方法归纳】
如图,在□ABCD中,有以下结论:
(1)△AOD的周长-△AOB的周长=AD-AB(AD>AB);
(2)S△AOB=S△AOD=S△BOC=S△COD=
S□ABCD;
(3)过点O的任意一条直线平分□ABCD的周长和面积;
(4)平行四边形一条对角线的两端点到另一条对角线的距离相等.
