2020-2021学年苏科教版七年级下册第九章整式乘法与因式分解课件(共25张ppt)
文档属性
| 名称 | 2020-2021学年苏科教版七年级下册第九章整式乘法与因式分解课件(共25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 715.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
因式分解
目录
整式乘除法
单项式×单项式
单项式×多项式
多项式×多项式
乘法公式
因式分解
提公因式法
公式法
十字相乘法
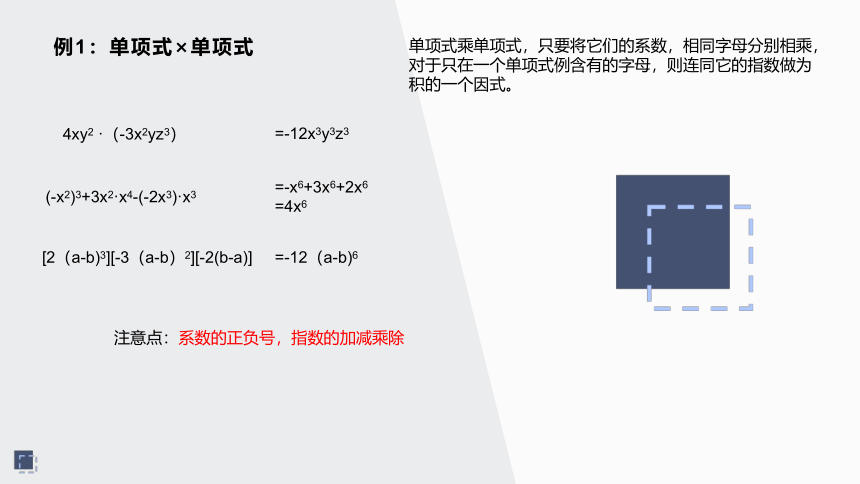
例1:单项式×单项式
4xy2
·(-3x2yz3)
=-12x3y3z3
(-x2)3+3x2·x4-(-2x3)·x3
=-x6+3x6+2x6
=4x6
[2(a-b)3][-3(a-b)2][-2(b-a)]
=-12(a-b)6
单项式乘单项式,只要将它们的系数,相同字母分别相乘,
对于只在一个单项式例含有的字母,则连同它的指数做为积的一个因式。
注意点:系数的正负号,指数的加减乘除
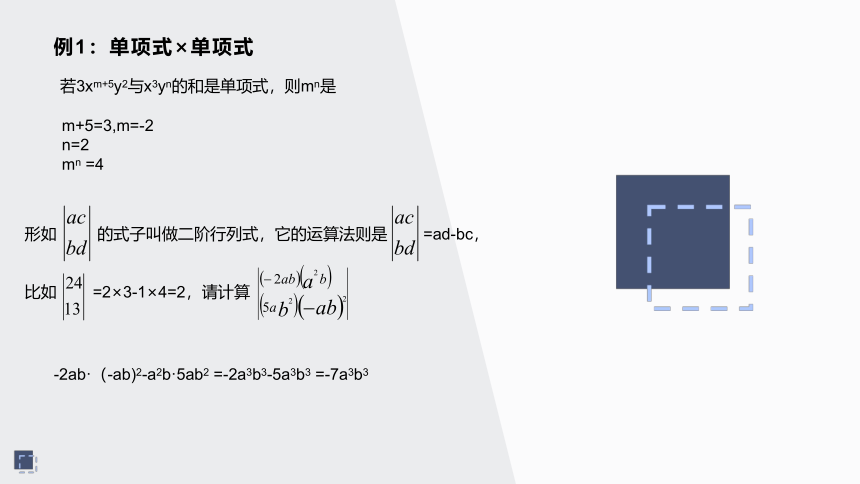
例1:单项式×单项式
若3xm+5y2与x3yn的和是单项式,则mn是
m+5=3,m=-2
n=2
mn
=4
形如
的式子叫做二阶行列式,它的运算法则是
=ad-bc,
比如
=2×3-1×4=2,请计算
-2ab·(-ab)2-a2b·5ab2
=-2a3b3-5a3b3
=-7a3b3
例2:单项式×多项式
(-x2-xy+y2)(-xy)
=x3y+x2y2-xy3
单项式与多项式相乘,用单项式去乘多项式的每一项,再把所得的积相加。
a(b+c+d)=ab+ac+ad
2mn(-2mn)2-3n(mn+m2n+m3n2)
=8m3n3-3mn2-3m2n2-3m3n3
=5m3n3-3mn2-3m2n2
例2:单项式×多项式
若要使x(x2+a+3)=x(x2+5)+2(b+2)成立,则a,b分别是多少?
原式可得:
a+3=5,a=2
b+2=0,b=-2
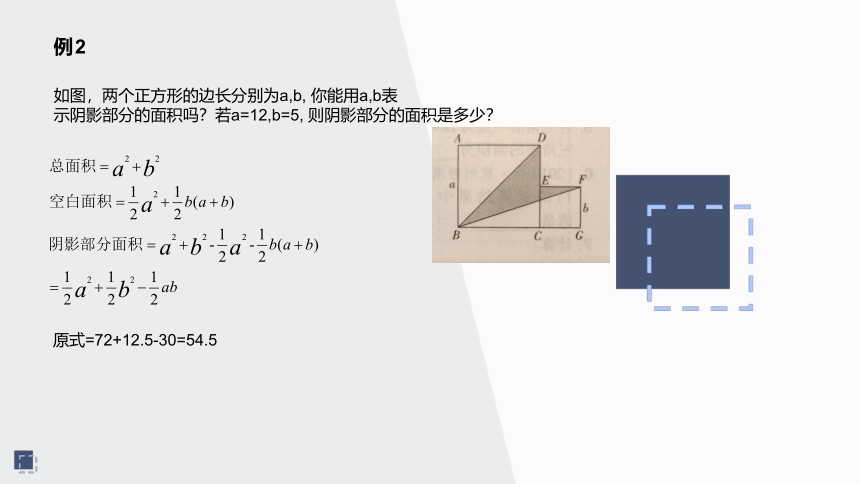
例2
如图,两个正方形的边长分别为a,b,
你能用a,b表
示阴影部分的面积吗?若a=12,b=5,
则阴影部分的面积是多少?
原式=72+12.5-30=54.5
例3:多项式×多项式
用一个多项式的每一项去乘另一个多项式的每一项,把所得的积相加。
(a+b)·(c+d)=ac+ad+bc+bd
(x-2y)(5a+3b)
=10ax+3bx-10ay-6by
(2x2-1)(3x2-2x+1)
=6x4-4x3+2x2-3x2+2x-1
=6x4-4x3-x2+2x-1
例3:
观察下列多项式的乘法计算:
①(x+3)(x+4)=x2+7x+12;
②(x+3)(x-4)=x2-x-12;
③(x-3)(x+4)=x2+x-12;
④(x-3)(x-4)=x2-7x+12.
根据你发现的规律,解决下列问题:
(1)(x+p)(x+q)=
(2)若(x+p)(x+q)=x-8x+15,
则p+q的值为
(3)利用规律计算:
①(x+2)(x+3)=
②(x-2)(x-3)=
③(x+2)(x-3)=
④(x-2)(x+3)=
x2+(p+q)x+pq
-8
x2+5x+6
x2-5x+6
x2-x-6
x2+x-6
乘法公式:
完全平方公式
(a±b)2=a2±2ab+b2
平方差公式
a2-b2=(a+b)(a-b)
例4:公式的应用
(a+3)2-(a-1)2
=(a+3+a-1)(a+3-a+1)
=8a+8
(a+2b-1)2
=a2+4b2+1+4ab-2a-4b
例4:
20202-2019×2021
=20202-(2020-1)(2020+1)
=20202-(20202-1)
=1
例5:综合运用
先化简,再求值.a=0.5
(a+3)2-(a+1)·(a-1)-2(2a+4)
=(a+2+1)2-4(a+2)-a2+1
=(a+2-1)2-a2
=(a+1+a)(a+1-a)
=2a+1
=2
提公因式法
①系数(数字)一各项系数最大公约数;②字母--各项含有的相同字母;③指数--相同字母的最低次数;步骤:第一步是找出公因式;第二步是提取公因式并确定另一因式.需注意,提取完公因式后,另一个因式的项数与原多项式的项数一致,这一点可用来检验是否漏项.
注意:①提取公因式后各因式应该是最简形式,即分解到“底”;②如果多项式的第一项的系数是负的,一般要提出“-”号,使括号内的第一项的系数是正的.
例1:提公因式法
(a-b)2-(b-a)
=(a-b)2+(a-b)
=(a-b)(a-b+1)
15a(a-b)2n+1-10ab(b-a)2n
=5a(a-b)2n·(3a-3b-2b)
=5a(a-b)2n·(3a-5b)
注意正负号,尤其是奇数次幂,偶数次幂的区别。
例1:
ab=3,a2b+ab2=15,求a2+b2
a2b+ab2=ab(a+b)
a+b=5
(a+b)2=25
a2+b2=25-2×3=19
39×37-13×81
=39×37-39×27
=390
公式法:
完全平方公式
(a±b)2=a2±2ab+b2
平方差公式
a2-b2=(a+b)(a-b)
例2:公式法
81-36x2+4x4
=(2x2-9)2
(x-y)2-2x+2y+1
=(x-y)2-2(x-y)+1
=(x-y-1)2
例2:
设y=kx,
是否存在实数k,
使得代数式(x2-y2)·(4x2-y2)+3x2(4x2-y2)能化简为x4?
若能,请求出所有满足条件的k2的值;若不能,请说明理由。
(x2-y2)·(4x2-y2)+3x2(4x2-y2)
=4x4-x2y2-4x2y2+y4+12x4-3x2y2
=4x4-k2x4-4k2x4+k4x4+12x4-3k2x4
=x4(16-8k2+k4)
=x4(k2-4)2
k2-4=1或k2-4=-1
k2=5或3
例2:公式法
设a=192×918,b=8882-302,c=6982-2202,则数a,b,c按从小到大的排列顺序为
a=361×918
b=(888+30)(888-30)=918×858
c=(698+220)(698-220)=918×478
所以a<c<b
例2:
从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算阴影部分的面积可以验证公式
(a+b)(a-b)=a2-b2
例2:
观察下列各式,探索发现规律:22-1=3=1×3;42-1=15=3×5;62-1=35=5×7;82-1=63=7×9;102-1=99=9×11;……用含正整数n的等式表示你所发现的规律为
.
(2n)2-1=(2n+1)(2n-1)
例2:
a,b,c为△ABC的三边长,且2a2+2b2+2c2=2ab+2ac+2bc,试判断△ABC的形状,并证明你的结论.
2a2+2b2+2c2=2ab+2ac+2bc
2a2+2b2+2c2
-2ab+2ac+2bc=0
a2+b2+c2
+a2+b2+c2
-2ab+2ac+2bc=0
(a-b)2+(a-c)2+(b-c)2=0
∴a=b=c,△ABC是等边三角形
十字相乘法
(x+a)(x+b)=x2+(a+b)x+ab
常用于一元二次方程
例3:十字相乘
x2-6x+8
=(x-4)(x-2)
x2+2x-143
=(x+13)(x-11)
因式分解
目录
整式乘除法
单项式×单项式
单项式×多项式
多项式×多项式
乘法公式
因式分解
提公因式法
公式法
十字相乘法
例1:单项式×单项式
4xy2
·(-3x2yz3)
=-12x3y3z3
(-x2)3+3x2·x4-(-2x3)·x3
=-x6+3x6+2x6
=4x6
[2(a-b)3][-3(a-b)2][-2(b-a)]
=-12(a-b)6
单项式乘单项式,只要将它们的系数,相同字母分别相乘,
对于只在一个单项式例含有的字母,则连同它的指数做为积的一个因式。
注意点:系数的正负号,指数的加减乘除
例1:单项式×单项式
若3xm+5y2与x3yn的和是单项式,则mn是
m+5=3,m=-2
n=2
mn
=4
形如
的式子叫做二阶行列式,它的运算法则是
=ad-bc,
比如
=2×3-1×4=2,请计算
-2ab·(-ab)2-a2b·5ab2
=-2a3b3-5a3b3
=-7a3b3
例2:单项式×多项式
(-x2-xy+y2)(-xy)
=x3y+x2y2-xy3
单项式与多项式相乘,用单项式去乘多项式的每一项,再把所得的积相加。
a(b+c+d)=ab+ac+ad
2mn(-2mn)2-3n(mn+m2n+m3n2)
=8m3n3-3mn2-3m2n2-3m3n3
=5m3n3-3mn2-3m2n2
例2:单项式×多项式
若要使x(x2+a+3)=x(x2+5)+2(b+2)成立,则a,b分别是多少?
原式可得:
a+3=5,a=2
b+2=0,b=-2
例2
如图,两个正方形的边长分别为a,b,
你能用a,b表
示阴影部分的面积吗?若a=12,b=5,
则阴影部分的面积是多少?
原式=72+12.5-30=54.5
例3:多项式×多项式
用一个多项式的每一项去乘另一个多项式的每一项,把所得的积相加。
(a+b)·(c+d)=ac+ad+bc+bd
(x-2y)(5a+3b)
=10ax+3bx-10ay-6by
(2x2-1)(3x2-2x+1)
=6x4-4x3+2x2-3x2+2x-1
=6x4-4x3-x2+2x-1
例3:
观察下列多项式的乘法计算:
①(x+3)(x+4)=x2+7x+12;
②(x+3)(x-4)=x2-x-12;
③(x-3)(x+4)=x2+x-12;
④(x-3)(x-4)=x2-7x+12.
根据你发现的规律,解决下列问题:
(1)(x+p)(x+q)=
(2)若(x+p)(x+q)=x-8x+15,
则p+q的值为
(3)利用规律计算:
①(x+2)(x+3)=
②(x-2)(x-3)=
③(x+2)(x-3)=
④(x-2)(x+3)=
x2+(p+q)x+pq
-8
x2+5x+6
x2-5x+6
x2-x-6
x2+x-6
乘法公式:
完全平方公式
(a±b)2=a2±2ab+b2
平方差公式
a2-b2=(a+b)(a-b)
例4:公式的应用
(a+3)2-(a-1)2
=(a+3+a-1)(a+3-a+1)
=8a+8
(a+2b-1)2
=a2+4b2+1+4ab-2a-4b
例4:
20202-2019×2021
=20202-(2020-1)(2020+1)
=20202-(20202-1)
=1
例5:综合运用
先化简,再求值.a=0.5
(a+3)2-(a+1)·(a-1)-2(2a+4)
=(a+2+1)2-4(a+2)-a2+1
=(a+2-1)2-a2
=(a+1+a)(a+1-a)
=2a+1
=2
提公因式法
①系数(数字)一各项系数最大公约数;②字母--各项含有的相同字母;③指数--相同字母的最低次数;步骤:第一步是找出公因式;第二步是提取公因式并确定另一因式.需注意,提取完公因式后,另一个因式的项数与原多项式的项数一致,这一点可用来检验是否漏项.
注意:①提取公因式后各因式应该是最简形式,即分解到“底”;②如果多项式的第一项的系数是负的,一般要提出“-”号,使括号内的第一项的系数是正的.
例1:提公因式法
(a-b)2-(b-a)
=(a-b)2+(a-b)
=(a-b)(a-b+1)
15a(a-b)2n+1-10ab(b-a)2n
=5a(a-b)2n·(3a-3b-2b)
=5a(a-b)2n·(3a-5b)
注意正负号,尤其是奇数次幂,偶数次幂的区别。
例1:
ab=3,a2b+ab2=15,求a2+b2
a2b+ab2=ab(a+b)
a+b=5
(a+b)2=25
a2+b2=25-2×3=19
39×37-13×81
=39×37-39×27
=390
公式法:
完全平方公式
(a±b)2=a2±2ab+b2
平方差公式
a2-b2=(a+b)(a-b)
例2:公式法
81-36x2+4x4
=(2x2-9)2
(x-y)2-2x+2y+1
=(x-y)2-2(x-y)+1
=(x-y-1)2
例2:
设y=kx,
是否存在实数k,
使得代数式(x2-y2)·(4x2-y2)+3x2(4x2-y2)能化简为x4?
若能,请求出所有满足条件的k2的值;若不能,请说明理由。
(x2-y2)·(4x2-y2)+3x2(4x2-y2)
=4x4-x2y2-4x2y2+y4+12x4-3x2y2
=4x4-k2x4-4k2x4+k4x4+12x4-3k2x4
=x4(16-8k2+k4)
=x4(k2-4)2
k2-4=1或k2-4=-1
k2=5或3
例2:公式法
设a=192×918,b=8882-302,c=6982-2202,则数a,b,c按从小到大的排列顺序为
a=361×918
b=(888+30)(888-30)=918×858
c=(698+220)(698-220)=918×478
所以a<c<b
例2:
从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算阴影部分的面积可以验证公式
(a+b)(a-b)=a2-b2
例2:
观察下列各式,探索发现规律:22-1=3=1×3;42-1=15=3×5;62-1=35=5×7;82-1=63=7×9;102-1=99=9×11;……用含正整数n的等式表示你所发现的规律为
.
(2n)2-1=(2n+1)(2n-1)
例2:
a,b,c为△ABC的三边长,且2a2+2b2+2c2=2ab+2ac+2bc,试判断△ABC的形状,并证明你的结论.
2a2+2b2+2c2=2ab+2ac+2bc
2a2+2b2+2c2
-2ab+2ac+2bc=0
a2+b2+c2
+a2+b2+c2
-2ab+2ac+2bc=0
(a-b)2+(a-c)2+(b-c)2=0
∴a=b=c,△ABC是等边三角形
十字相乘法
(x+a)(x+b)=x2+(a+b)x+ab
常用于一元二次方程
例3:十字相乘
x2-6x+8
=(x-4)(x-2)
x2+2x-143
=(x+13)(x-11)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
