18.1.1平行四边形的性质第2课时课件(30张)
文档属性
| 名称 | 18.1.1平行四边形的性质第2课时课件(30张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 343.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 00:00:00 | ||
图片预览






文档简介
八年级下册
平行四边形的性质
第2课时
学习目标
1.掌握平行四边形对边相等、对角相等的基础上,掌握对角线互相平分的性质,初步会运用这些性质进行有关的论证和计算;
2.培养综合运用知识的能力。
1、如图, □ABCD的周长为16 cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A.4 cm B.6 cm C.8 cm D.10 cm
2.在□ABCD中,对角线AC、BD相交于点O,已知AB=8cm,BC=6cm, △AOB周长为18cm,那么△AOD的周长为 cm.
预习反馈
C
16
你来评一评
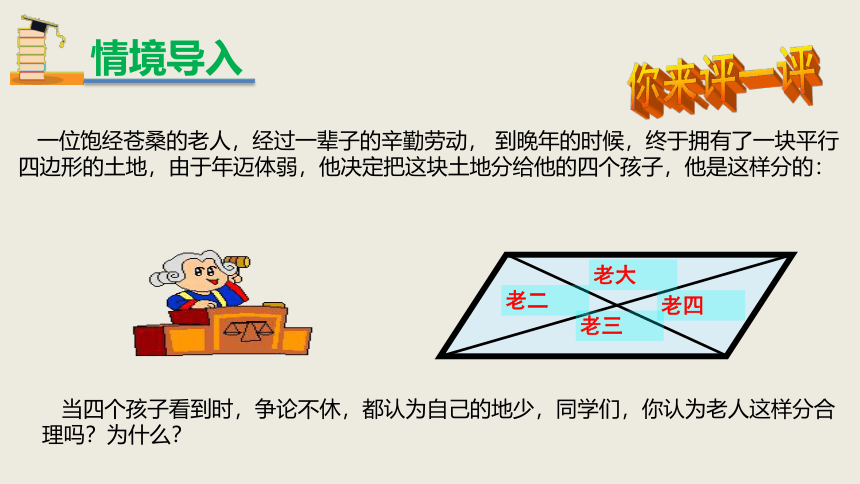
一位饱经苍桑的老人,经过一辈子的辛勤劳动, 到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
老大
老二
老三
老四
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么?
情境导入
A
C
D
B
如图, □ABCD的对角线AC、BD相交于点O.
O
猜一猜:
线段OA与OC、OB与OD长度有何关系?
●
量一量:
拿出手中的平行四边形纸片,测量出四条线段的长度,验证你的猜想是否正确.
课堂探究
知识点一:平行四边形的对角线的性质
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
动手试试
●
A
D
O
C
B
D
B
O
C
A
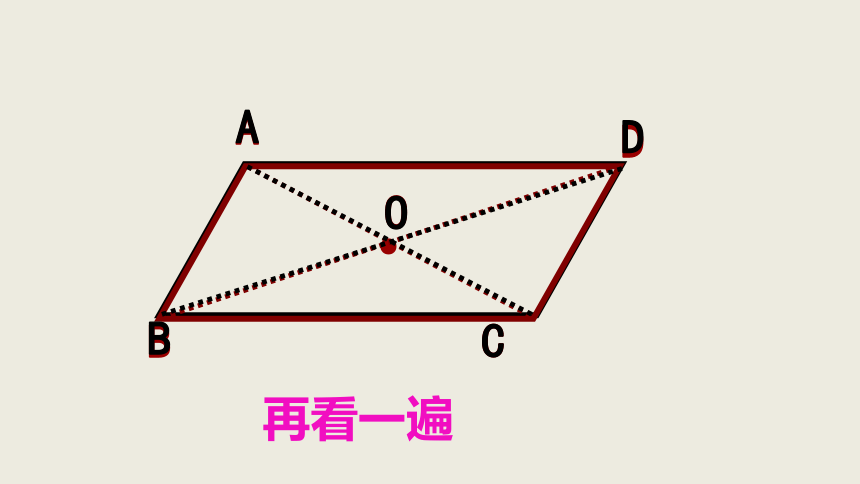
再看一遍
你能证明它吗?
●
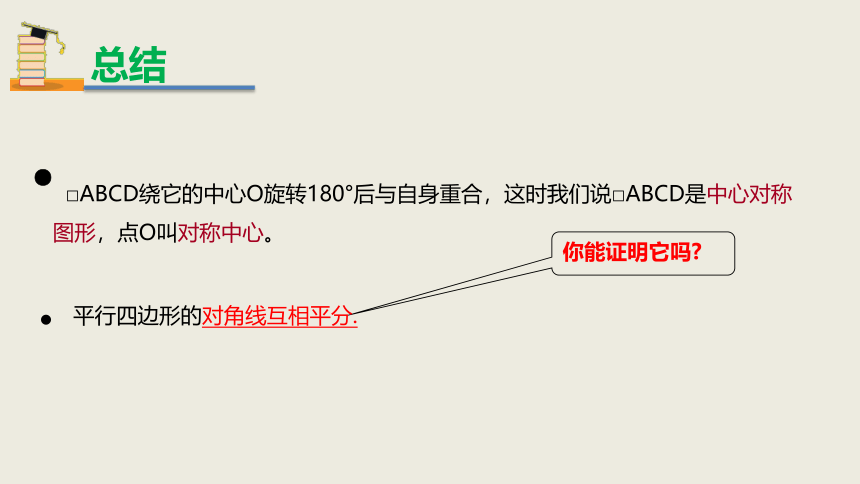
平行四边形的对角线互相平分.
●
□ABCD绕它的中心O旋转180°后与自身重合,这时我们说□ABCD是中心对称图形,点O叫对称中心。
总结
A
C
D
B
O
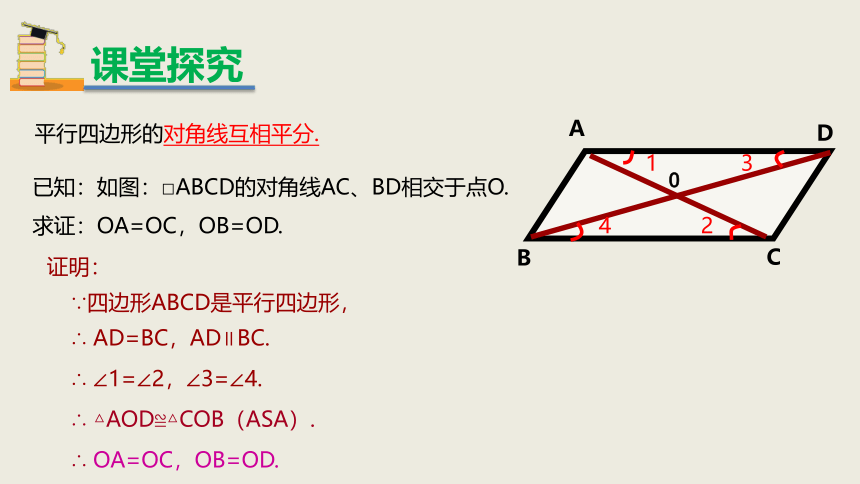
已知:如图:□ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
3
2
4
1
平行四边形的对角线互相平分.
课堂探究
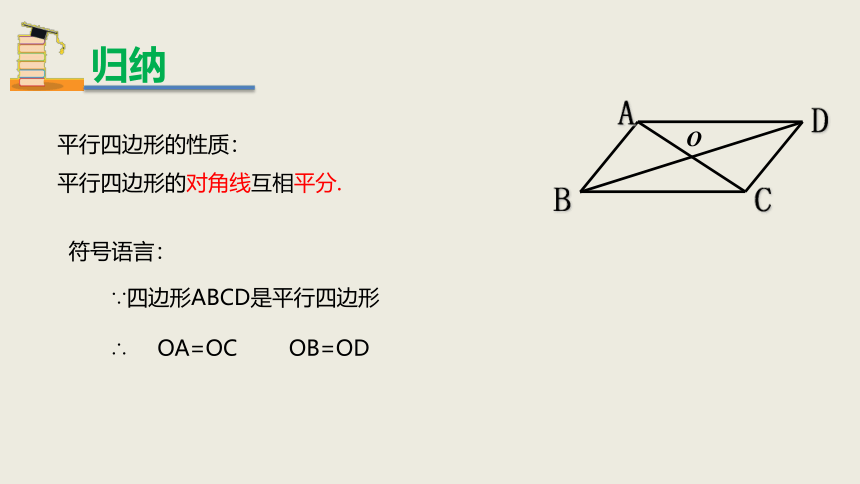
平行四边形的性质:
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形
OA=OC
OB=OD
∴
A
D
B
C
O
归纳
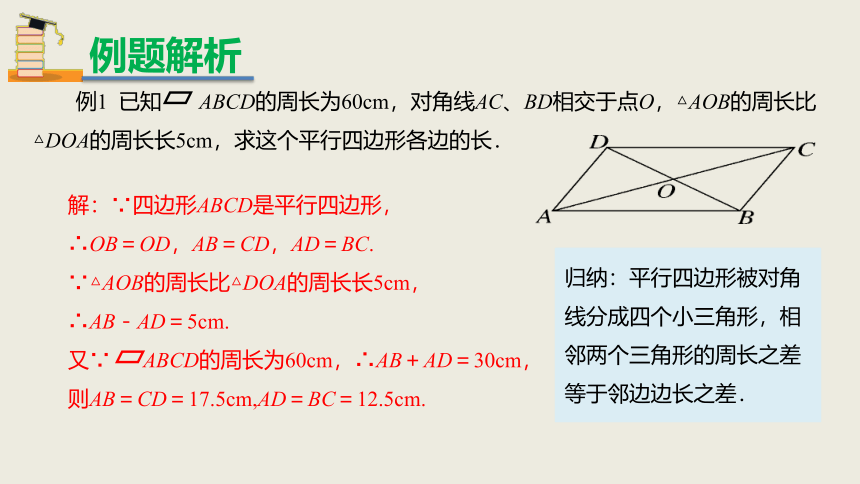
例1 已知 ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,求这个平行四边形各边的长.
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC.
∵△AOB的周长比△DOA的周长长5cm,
∴AB-AD=5cm.
又∵ ABCD的周长为60cm,∴AB+AD=30cm,
则AB=CD=17.5cm,AD=BC=12.5cm.
归纳:平行四边形被对角线分成四个小三角形,相邻两个三角形的周长之差等于邻边边长之差.
例题解析
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,平行四边形ABCD的周长是100cm,△AOB与△BOC的周长的和是122cm,且AC:DB= 2:1,求AC和BD的长.
解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,OB=OD,
∴AB+BC=50.
∵△AOB与△BOC的周长的和是122cm,
∴OA+OB+AB+OB+OC+BC=122,
即AC+BD=122-50=72.
又∵AC:DB=2:1,
∴AC=48cm,BD=24cm.
变式训练
例2 如图,平行四边形ABCD中,AC、BD交于O点,点E、F分别是AO、CO的中点,试判断线段BE、DF的关系并证明你的结论.
解:BE=DF,BE∥DF.
理由如下:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴OE=OF.
在△OFD和△OEB中,
OE=OF,∠DOF=∠BOE,OD=OB,
∴△OFD≌△OEB,
∴∠OEB=∠OFD,BE=DF,∴BE∥DF.
例题解析
例3 如图, ABCD的对角线AC,BD交于点O.点O作直线EF,分别交AB,CD于点E,F.求证:OE=OF.
A
B
C
D
F
E
O
证明:∵四边形ABCD是平行四边形,
∴∠ODF=∠OBE, ∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴AB∥CD, OD=OB,
∴OE=OF.
思考 改变直线EF的位置,OE=OF还成立吗?
A
B
C
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
请判断下列图中,OE=OF还成立么?
同例3易证明OE=OF还成立.
归纳:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等.
课堂探究
1.如图,平行四边形ABCD的对角线AC,BD交于点O,若AD=16,AC=24,BD=12,则△OBC的周长为( )
A.26 B.34 C.40 D.52
B
2.如图,在?ABCD中,对角线AC和BD相交于点O,△AOB的周长为15,AB=6,则对角线AC、BD的长度的和是( )
A.9 B.18 C.27 D.36
B
试一试
如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及□ABCD的面积.
∴△ABC是直角三角形
又∵AC⊥BC
解:∵四边形ABCD是平行四边形
∴BC=AD=8,CD=AB=10
又∵OA=OC
∴????????=????????2?????????2=102?82=6
?
∴OA=12????????=3
?
∴????□????????????????= BC×AC=8×6=48
?
课堂探究
知识点二:平行四边形的面积
例4如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若平行四边形ABCD的周长为48,DE=5,DF=10,求平行四边形ABCD的面积.
解:设AB=x,则BC=24-x.
根据平行四边形的面积公式可得5x=10(24-x),
解得x=16.
则平行四边形ABCD的面积为5×16=80.
归纳:已知平行四边形的高DE,DF,根据“等面积法”及平行四边形的性质列方程求解.
例题解析
一位饱经苍桑的老人,经过一辈子的辛勤劳动, 到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
老大
老二
老三
老四
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么?
问题再现
A
C
D
B
O
●
老大
老四
老三
老二
M
老人分地合理吗?
解:合理.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵△ADO与△ODC等底同高,
∴S△ADO=S△ODC.
同理可得S△ADO=S△ODC=S△BCO=S△AOB.
还可结合全等来证哟.
归纳:平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.
A
B
C
D
O
F
E
例6 如图,AC,BD交于点O,EF过点O,平行四边形ABCD被EF所分的两个四边形面积相等吗?
M
N
解:设直线EF交AD,BC于点N,M.
∵AD∥BC,
∴∠NAO=∠MCO,∠ANO=∠CMO.
又∵AO=CO,
∴△NAO≌△MCO,
∴S四边形ANMB=S△NAO+S△AOB+S△MOB=S△MCO+S△AOB+S△MOB=S△AOB+S△COB= .
∴S四边形ANMB=S四边形CMND,
即平行四边形ABCD被EF所分的两个四边形面积相等.
拓展延伸
A
B
D
O
E
F
A
B
C
D
O
E
F
C
A
B
C
D
O
E
F
思考 如图,AC,BD交于点O,EF过点O,平行四边形ABCD被EF所分的两个四边形面积相等吗?
归纳:过对角线交点的任一条直线都将平行四边形分成面积相等的两部分.
同例5易求得平行四边形ABCD被EF所分的两个四边形面积相等.
1.把一个平行四边形分成3个三角形,已知两个阴影三角形的面积分别是9cm2和12cm2,求平行四边形的面积.
解:(9+12)×2
=21×2
=42(cm2)
答:平行四边形的面积是42cm2.
试一试
2.如图,欢欢看到平行四边形的草地中间有一水井,为了浇水的方便,欢欢建议我们经过水井修小路,一样可以把草地分成面积相等的两部分,同学们,你知道聪明的欢欢是怎么分的吗?
B
M
C
●
D
A
O
解:如图所示.
1.平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度
2.若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8
随堂检测
B
D
3.如图,在□ ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是__________________.
4.如图,在□ABCD中, 对角线AC﹑BD相交于点O,且AC+BD=20, △AOB的周长等于15,则CD=______.
1<AD<9
5
5.如图,在 ABCD中,AE⊥BC于E,AF⊥CD于F,BE=2 cm,DF=3 cm,∠EAF=60°,试求CF的长.
解:∵∠EAF=60°,AE⊥BC,AF⊥CD,
∴∠C=120°.∴∠B=60°.
∴∠BAE=30°.
∴AB=2BE=4(cm).
∴CD=4(cm).
∴CF=1(cm).
课堂小结
本节课我们学习了什么?你有什么收获呢?
平行四边形的性质共有哪些?
边:
角:
对角线:
对边平行,对边相等
对角相等,邻角互补
对角线互相平分
书面作业:完成相关书本作业
布置作业
再见
平行四边形的性质
第2课时
学习目标
1.掌握平行四边形对边相等、对角相等的基础上,掌握对角线互相平分的性质,初步会运用这些性质进行有关的论证和计算;
2.培养综合运用知识的能力。
1、如图, □ABCD的周长为16 cm,AC、BD相交于点O,OE⊥AC交AD于E,则△DCE的周长为( )
A.4 cm B.6 cm C.8 cm D.10 cm
2.在□ABCD中,对角线AC、BD相交于点O,已知AB=8cm,BC=6cm, △AOB周长为18cm,那么△AOD的周长为 cm.
预习反馈
C
16
你来评一评
一位饱经苍桑的老人,经过一辈子的辛勤劳动, 到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
老大
老二
老三
老四
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么?
情境导入
A
C
D
B
如图, □ABCD的对角线AC、BD相交于点O.
O
猜一猜:
线段OA与OC、OB与OD长度有何关系?
●
量一量:
拿出手中的平行四边形纸片,测量出四条线段的长度,验证你的猜想是否正确.
课堂探究
知识点一:平行四边形的对角线的性质
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
动手试试
●
A
D
O
C
B
D
B
O
C
A
再看一遍
你能证明它吗?
●
平行四边形的对角线互相平分.
●
□ABCD绕它的中心O旋转180°后与自身重合,这时我们说□ABCD是中心对称图形,点O叫对称中心。
总结
A
C
D
B
O
已知:如图:□ABCD的对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
证明:
∵四边形ABCD是平行四边形,
∴ AD=BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴ △AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
3
2
4
1
平行四边形的对角线互相平分.
课堂探究
平行四边形的性质:
平行四边形的对角线互相平分.
符号语言:
∵四边形ABCD是平行四边形
OA=OC
OB=OD
∴
A
D
B
C
O
归纳
例1 已知 ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△DOA的周长长5cm,求这个平行四边形各边的长.
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC.
∵△AOB的周长比△DOA的周长长5cm,
∴AB-AD=5cm.
又∵ ABCD的周长为60cm,∴AB+AD=30cm,
则AB=CD=17.5cm,AD=BC=12.5cm.
归纳:平行四边形被对角线分成四个小三角形,相邻两个三角形的周长之差等于邻边边长之差.
例题解析
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,平行四边形ABCD的周长是100cm,△AOB与△BOC的周长的和是122cm,且AC:DB= 2:1,求AC和BD的长.
解:∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD,OB=OD,
∴AB+BC=50.
∵△AOB与△BOC的周长的和是122cm,
∴OA+OB+AB+OB+OC+BC=122,
即AC+BD=122-50=72.
又∵AC:DB=2:1,
∴AC=48cm,BD=24cm.
变式训练
例2 如图,平行四边形ABCD中,AC、BD交于O点,点E、F分别是AO、CO的中点,试判断线段BE、DF的关系并证明你的结论.
解:BE=DF,BE∥DF.
理由如下:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∴OE=OF.
在△OFD和△OEB中,
OE=OF,∠DOF=∠BOE,OD=OB,
∴△OFD≌△OEB,
∴∠OEB=∠OFD,BE=DF,∴BE∥DF.
例题解析
例3 如图, ABCD的对角线AC,BD交于点O.点O作直线EF,分别交AB,CD于点E,F.求证:OE=OF.
A
B
C
D
F
E
O
证明:∵四边形ABCD是平行四边形,
∴∠ODF=∠OBE, ∠DFO=∠BEO,
∴△DOF≌△BOE(AAS),
∴AB∥CD, OD=OB,
∴OE=OF.
思考 改变直线EF的位置,OE=OF还成立吗?
A
B
C
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
请判断下列图中,OE=OF还成立么?
同例3易证明OE=OF还成立.
归纳:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等.
课堂探究
1.如图,平行四边形ABCD的对角线AC,BD交于点O,若AD=16,AC=24,BD=12,则△OBC的周长为( )
A.26 B.34 C.40 D.52
B
2.如图,在?ABCD中,对角线AC和BD相交于点O,△AOB的周长为15,AB=6,则对角线AC、BD的长度的和是( )
A.9 B.18 C.27 D.36
B
试一试
如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及□ABCD的面积.
∴△ABC是直角三角形
又∵AC⊥BC
解:∵四边形ABCD是平行四边形
∴BC=AD=8,CD=AB=10
又∵OA=OC
∴????????=????????2?????????2=102?82=6
?
∴OA=12????????=3
?
∴????□????????????????= BC×AC=8×6=48
?
课堂探究
知识点二:平行四边形的面积
例4如图,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若平行四边形ABCD的周长为48,DE=5,DF=10,求平行四边形ABCD的面积.
解:设AB=x,则BC=24-x.
根据平行四边形的面积公式可得5x=10(24-x),
解得x=16.
则平行四边形ABCD的面积为5×16=80.
归纳:已知平行四边形的高DE,DF,根据“等面积法”及平行四边形的性质列方程求解.
例题解析
一位饱经苍桑的老人,经过一辈子的辛勤劳动, 到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
老大
老二
老三
老四
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么?
问题再现
A
C
D
B
O
●
老大
老四
老三
老二
M
老人分地合理吗?
解:合理.理由如下:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵△ADO与△ODC等底同高,
∴S△ADO=S△ODC.
同理可得S△ADO=S△ODC=S△BCO=S△AOB.
还可结合全等来证哟.
归纳:平行四边形的对角线分平行四边形为四个面积相等的三角形,且都等于平行四边形面积的四分之一.相对的两个三角形全等.
A
B
C
D
O
F
E
例6 如图,AC,BD交于点O,EF过点O,平行四边形ABCD被EF所分的两个四边形面积相等吗?
M
N
解:设直线EF交AD,BC于点N,M.
∵AD∥BC,
∴∠NAO=∠MCO,∠ANO=∠CMO.
又∵AO=CO,
∴△NAO≌△MCO,
∴S四边形ANMB=S△NAO+S△AOB+S△MOB=S△MCO+S△AOB+S△MOB=S△AOB+S△COB= .
∴S四边形ANMB=S四边形CMND,
即平行四边形ABCD被EF所分的两个四边形面积相等.
拓展延伸
A
B
D
O
E
F
A
B
C
D
O
E
F
C
A
B
C
D
O
E
F
思考 如图,AC,BD交于点O,EF过点O,平行四边形ABCD被EF所分的两个四边形面积相等吗?
归纳:过对角线交点的任一条直线都将平行四边形分成面积相等的两部分.
同例5易求得平行四边形ABCD被EF所分的两个四边形面积相等.
1.把一个平行四边形分成3个三角形,已知两个阴影三角形的面积分别是9cm2和12cm2,求平行四边形的面积.
解:(9+12)×2
=21×2
=42(cm2)
答:平行四边形的面积是42cm2.
试一试
2.如图,欢欢看到平行四边形的草地中间有一水井,为了浇水的方便,欢欢建议我们经过水井修小路,一样可以把草地分成面积相等的两部分,同学们,你知道聪明的欢欢是怎么分的吗?
B
M
C
●
D
A
O
解:如图所示.
1.平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度
2.若平行四边形的一边长为5,则它的两条对角线长可以是( )
A. 12和2 B. 3和4
C. 4和6 D. 4和8
随堂检测
B
D
3.如图,在□ ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是__________________.
4.如图,在□ABCD中, 对角线AC﹑BD相交于点O,且AC+BD=20, △AOB的周长等于15,则CD=______.
1<AD<9
5
5.如图,在 ABCD中,AE⊥BC于E,AF⊥CD于F,BE=2 cm,DF=3 cm,∠EAF=60°,试求CF的长.
解:∵∠EAF=60°,AE⊥BC,AF⊥CD,
∴∠C=120°.∴∠B=60°.
∴∠BAE=30°.
∴AB=2BE=4(cm).
∴CD=4(cm).
∴CF=1(cm).
课堂小结
本节课我们学习了什么?你有什么收获呢?
平行四边形的性质共有哪些?
边:
角:
对角线:
对边平行,对边相等
对角相等,邻角互补
对角线互相平分
书面作业:完成相关书本作业
布置作业
再见
