18.1.2平行四边形的判定课件(21张)
文档属性
| 名称 | 18.1.2平行四边形的判定课件(21张) |  | |
| 格式 | ppt | ||
| 文件大小 | 586.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 12:20:40 | ||
图片预览



文档简介
(共21张PPT)
18.1.2
平行四边形的判定(1)
1、经历并了解平行四边形的判别方法探索过程,逐步掌握说理的基本方法。
2、掌握平行四边形的判定方法1和2,能根据判别方法进行有关的应用。
学习目标:
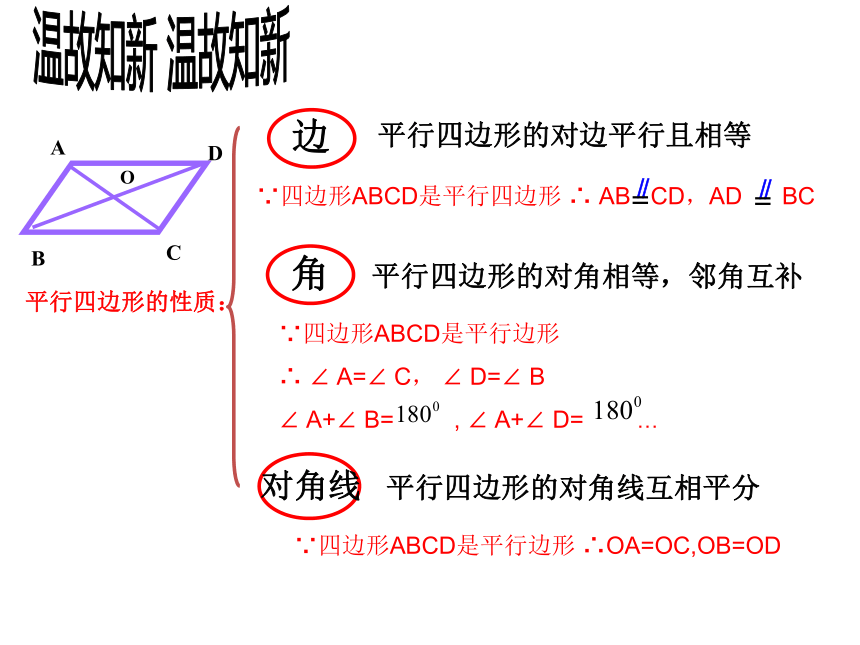
边
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
温故知新
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形
∴
AB
CD,AD
BC
∥
﹦
∥
﹦
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴
∠
A=∠
C,
∠
D=∠
B
∠
A+∠
B=
,
∠
A+∠
D=
…
∵四边形ABCD是平行边形
∴OA=OC,OB=OD
我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
(1)根据定义:两组对边分别平行的四边形叫做平行四边形
因为AB//CD,AD//BC;
所以四边形ABCD是平行四边形。
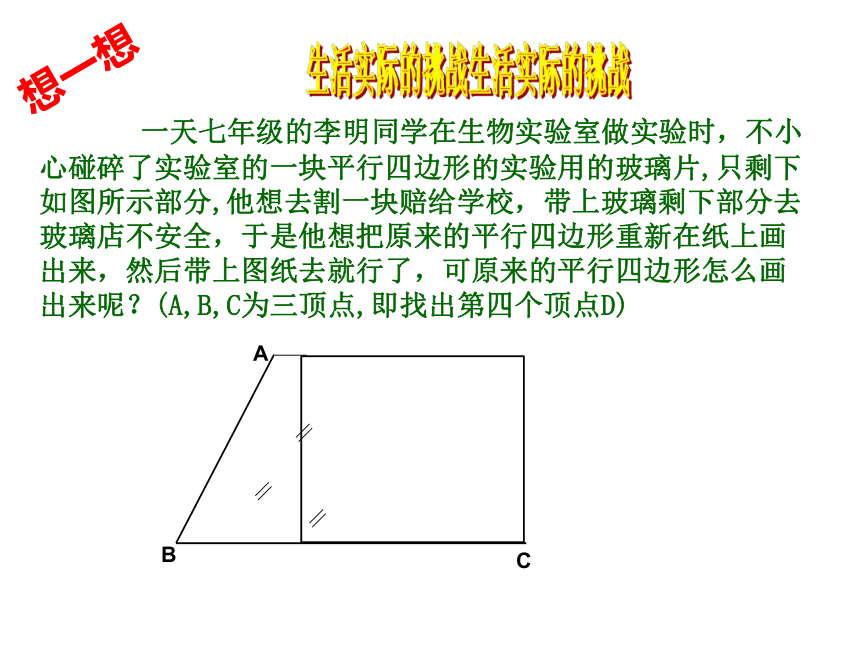
一天七年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)
生活实际的挑战
A
B
C
想一想
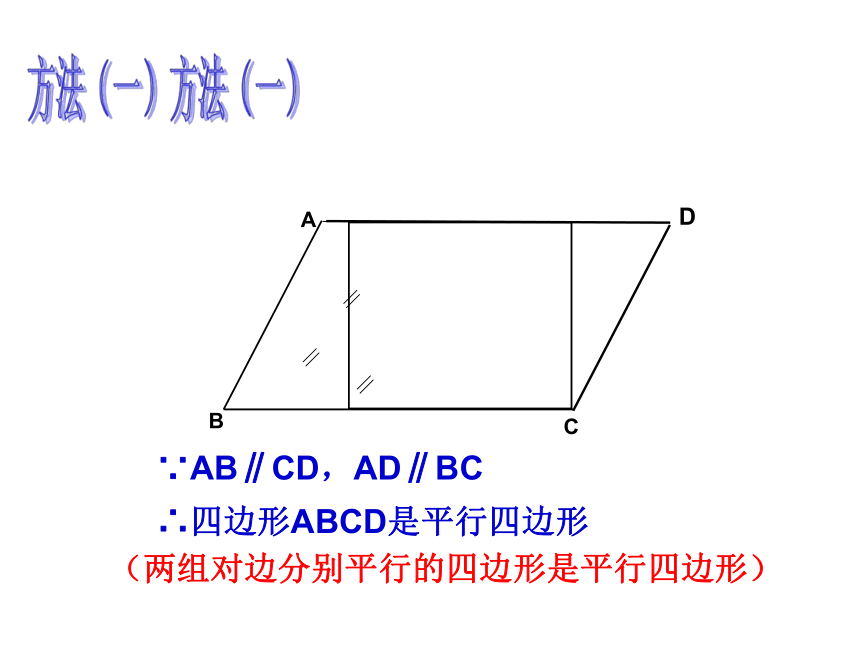
方法(一)
D
A
B
C
(两组对边分别平行的四边形是平行四边形)
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
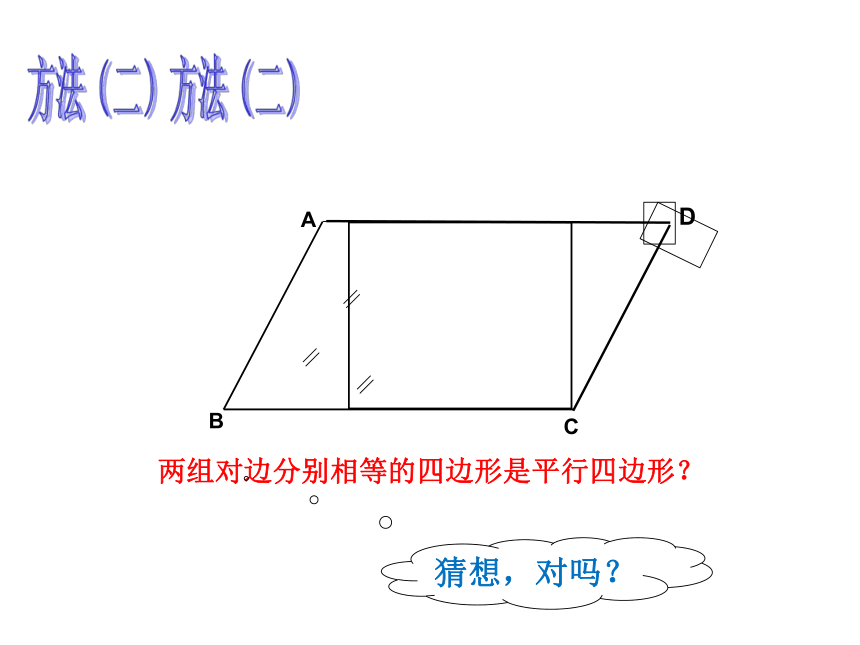
方法(二)
D
A
B
C
两组对边分别相等的四边形是平行四边形?
猜想,对吗?
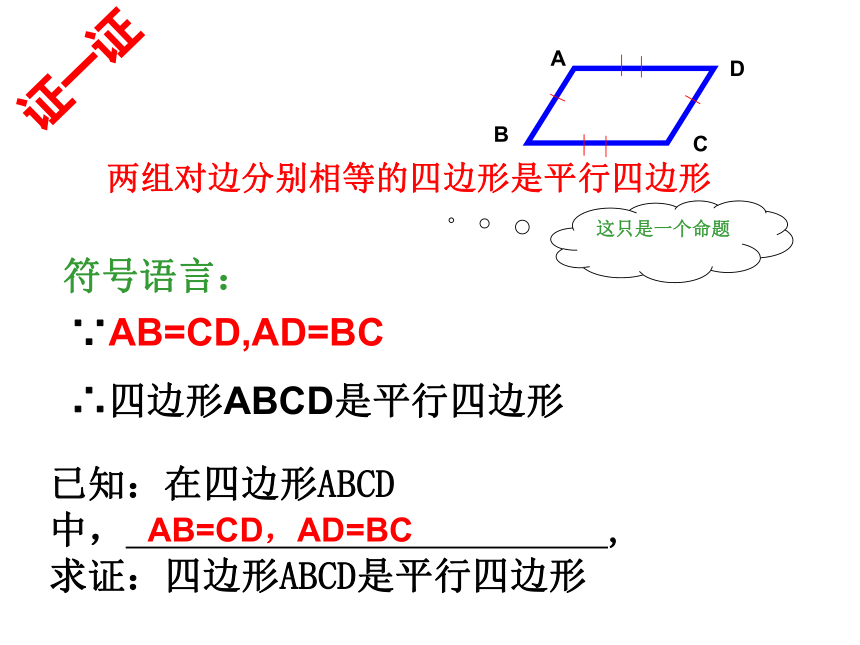
两组对边分别相等的四边形是平行四边形
这只是一个命题
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
已知:在四边形ABCD中,
,
求证:四边形ABCD是平行四边形
A
B
C
D
符号语言:
AB=CD,AD=BC
证一证
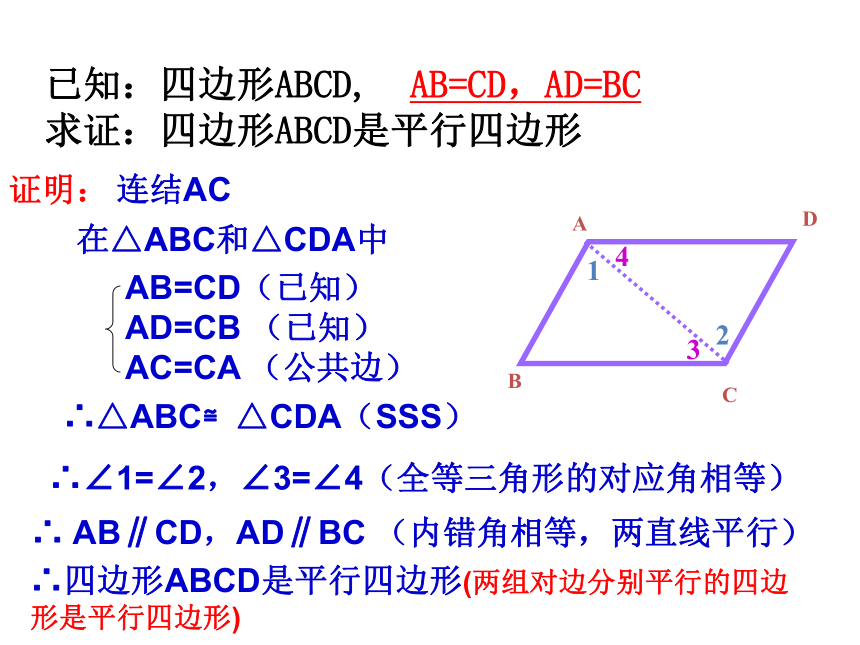
已知:四边形ABCD,
AB=CD,AD=BC
求证:四边形ABCD是平行四边形
证明:
连结AC
在△ABC和△CDA中
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴
AB∥CD,AD∥BC
(内错角相等,两直线平行)
D
B
A
C
2
1
3
4
AB=CD(已知)
AD=CB
(已知)
AC=CA
(公共边)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
两组对边分别相等的四边形是平行四边形
平行四边形的判定定理1:
符号语言:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
A
B
C
D
方法(三)
D
O
A
B
C
对角线互相平分的四边形是平行四边形?
猜想,对吗?
O
已知:四边形ABCD,
对角线AC、BD相交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:
在△AOD和△COB中
OA=OC
∠AOD=∠COB
OD=OB
∴△AOD≌△COB
∴∠1=∠2
∴
AD∥CB
∴四边形ABCD是平行四边形
B
A
C
2
1
D
同理
AB
∥CD
对角线互相平分的四边形是平行四边形
平行四边形的判定定理2:
符号语言:
A
B
C
D
O
∵
OA=OC,OB=OD
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
O
从边来判定
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
理一理
平行四边形的判定方法
1.如图,AB
=DC=EF,
AD=BC,DE=CF,则图中有哪些互相平行的线段?
看谁最快
AB
∥
DC∥
EF
AD
∥
BC
DE
∥
CF
2、请你识别下列四边形哪些是平行四边形?为什么?
A
D
C
B
110°
70°
110°
⑴
⑶
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
⑵
3、在下列条件中,
判定四边形是平行四边形的是
AB∥CD,AD∥BC
AB=CD,AD=BC
B
D
A
C
(两组对边分别平行)
(两组对边分别相等)
4、在平行四边形中,AC,BD相交与点O。
A
B
C
D
O
⑴若AD=8㎝,AB=4㎝,那么当BC=
㎝,CD=
㎝时,四边形ABCD是平行四边形。
⑵若AC=10㎝,BD=8㎝,那么当AO=
㎝
,DO=
㎝时,四边形ABCD是平行四边形
8
4
5
4
大显身手
D
A
B
C
E
F
证法1:
在
ABCD中
AD
∥
BC且AD
=BC
EAD=
FCB
AE=CF
EAD=
FCB
AD=BC
AED
≌
CFB(SAS)
DE=BF
四边形BFDE是平行四边形
在
AED和
CFB中
同理可证:BE=DF
5.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
大显身手
5.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
证法2:连接BD,交AC于点O。
∵在
ABCD
中
∴
AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
∴
四边形BFDE是平行四边形
说一说:
1.本节课你学会了几种平行四边形的判定方法
2.本节课所学的解决问题的思路是:
(2)碰到平行四边形的问题常转化为三角形来解决。
(1)解决一个数学问题,常要通过“动手实践”----“
猜想”----“验证猜想(证明)”-----“得出结论”
18.1.2
平行四边形的判定(1)
1、经历并了解平行四边形的判别方法探索过程,逐步掌握说理的基本方法。
2、掌握平行四边形的判定方法1和2,能根据判别方法进行有关的应用。
学习目标:
边
平行四边形的对边平行且相等
角
对角线
平行四边形的对角线互相平分
温故知新
平行四边形的性质:
B
D
A
C
O
∵四边形ABCD是平行四边形
∴
AB
CD,AD
BC
∥
﹦
∥
﹦
平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴
∠
A=∠
C,
∠
D=∠
B
∠
A+∠
B=
,
∠
A+∠
D=
…
∵四边形ABCD是平行边形
∴OA=OC,OB=OD
我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
(1)根据定义:两组对边分别平行的四边形叫做平行四边形
因为AB//CD,AD//BC;
所以四边形ABCD是平行四边形。
一天七年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)
生活实际的挑战
A
B
C
想一想
方法(一)
D
A
B
C
(两组对边分别平行的四边形是平行四边形)
∵AB∥CD,AD∥BC
∴四边形ABCD是平行四边形
方法(二)
D
A
B
C
两组对边分别相等的四边形是平行四边形?
猜想,对吗?
两组对边分别相等的四边形是平行四边形
这只是一个命题
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
已知:在四边形ABCD中,
,
求证:四边形ABCD是平行四边形
A
B
C
D
符号语言:
AB=CD,AD=BC
证一证
已知:四边形ABCD,
AB=CD,AD=BC
求证:四边形ABCD是平行四边形
证明:
连结AC
在△ABC和△CDA中
∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴
AB∥CD,AD∥BC
(内错角相等,两直线平行)
D
B
A
C
2
1
3
4
AB=CD(已知)
AD=CB
(已知)
AC=CA
(公共边)
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
两组对边分别相等的四边形是平行四边形
平行四边形的判定定理1:
符号语言:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
(两组对边分别相等的四边形是平行四边形)
A
B
C
D
方法(三)
D
O
A
B
C
对角线互相平分的四边形是平行四边形?
猜想,对吗?
O
已知:四边形ABCD,
对角线AC、BD相交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:
在△AOD和△COB中
OA=OC
∠AOD=∠COB
OD=OB
∴△AOD≌△COB
∴∠1=∠2
∴
AD∥CB
∴四边形ABCD是平行四边形
B
A
C
2
1
D
同理
AB
∥CD
对角线互相平分的四边形是平行四边形
平行四边形的判定定理2:
符号语言:
A
B
C
D
O
∵
OA=OC,OB=OD
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
O
从边来判定
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
理一理
平行四边形的判定方法
1.如图,AB
=DC=EF,
AD=BC,DE=CF,则图中有哪些互相平行的线段?
看谁最快
AB
∥
DC∥
EF
AD
∥
BC
DE
∥
CF
2、请你识别下列四边形哪些是平行四边形?为什么?
A
D
C
B
110°
70°
110°
⑴
⑶
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
7.6㎝
7.6㎝
⑵
3、在下列条件中,
判定四边形是平行四边形的是
AB∥CD,AD∥BC
AB=CD,AD=BC
B
D
A
C
(两组对边分别平行)
(两组对边分别相等)
4、在平行四边形中,AC,BD相交与点O。
A
B
C
D
O
⑴若AD=8㎝,AB=4㎝,那么当BC=
㎝,CD=
㎝时,四边形ABCD是平行四边形。
⑵若AC=10㎝,BD=8㎝,那么当AO=
㎝
,DO=
㎝时,四边形ABCD是平行四边形
8
4
5
4
大显身手
D
A
B
C
E
F
证法1:
在
ABCD中
AD
∥
BC且AD
=BC
EAD=
FCB
AE=CF
EAD=
FCB
AD=BC
AED
≌
CFB(SAS)
DE=BF
四边形BFDE是平行四边形
在
AED和
CFB中
同理可证:BE=DF
5.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
大显身手
5.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
D
O
A
B
C
E
F
证法2:连接BD,交AC于点O。
∵在
ABCD
中
∴
AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
∴
四边形BFDE是平行四边形
说一说:
1.本节课你学会了几种平行四边形的判定方法
2.本节课所学的解决问题的思路是:
(2)碰到平行四边形的问题常转化为三角形来解决。
(1)解决一个数学问题,常要通过“动手实践”----“
猜想”----“验证猜想(证明)”-----“得出结论”
