18.1.1平行四边形的性质课件(22张)
文档属性
| 名称 | 18.1.1平行四边形的性质课件(22张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 00:00:00 | ||
图片预览



文档简介
平行四边形的性质
观察下列图形
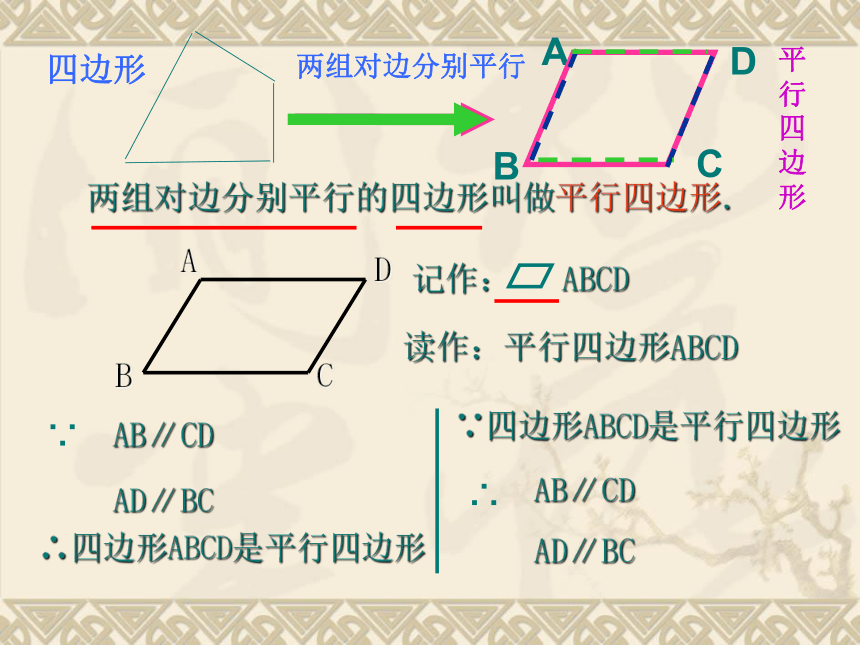
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
两组对边分别平行
四边形
C
B
A
D
平行四边形
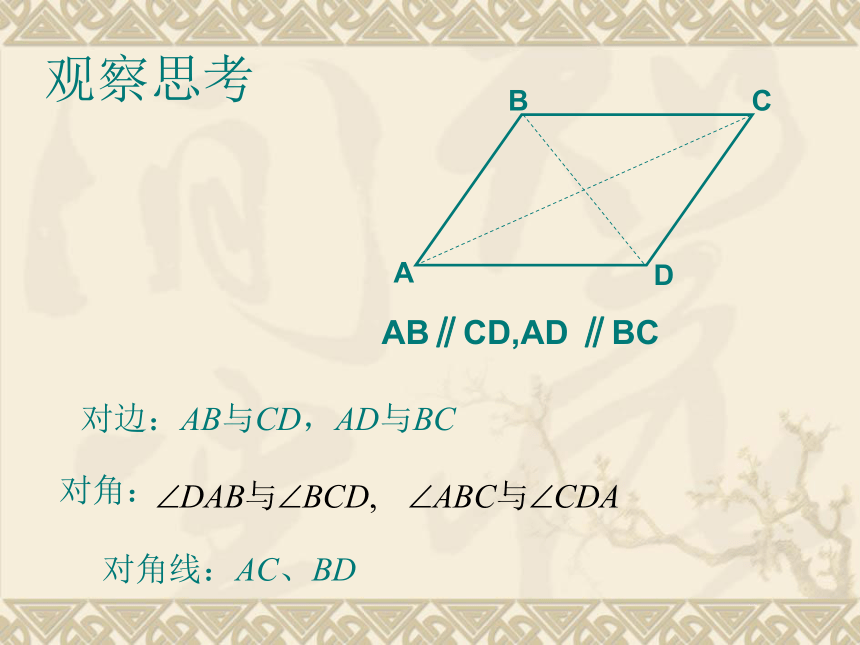
AB∥CD,AD ∥BC
观察思考
对边:AB与CD,AD与BC
对角:
对角线:AC、BD
C
B
D
A
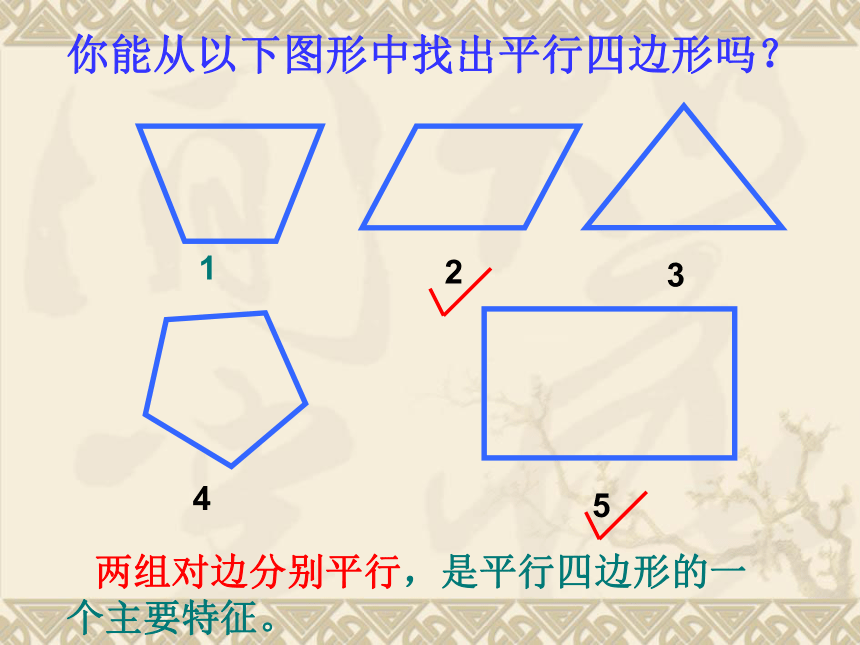
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
2
3
1
4
5
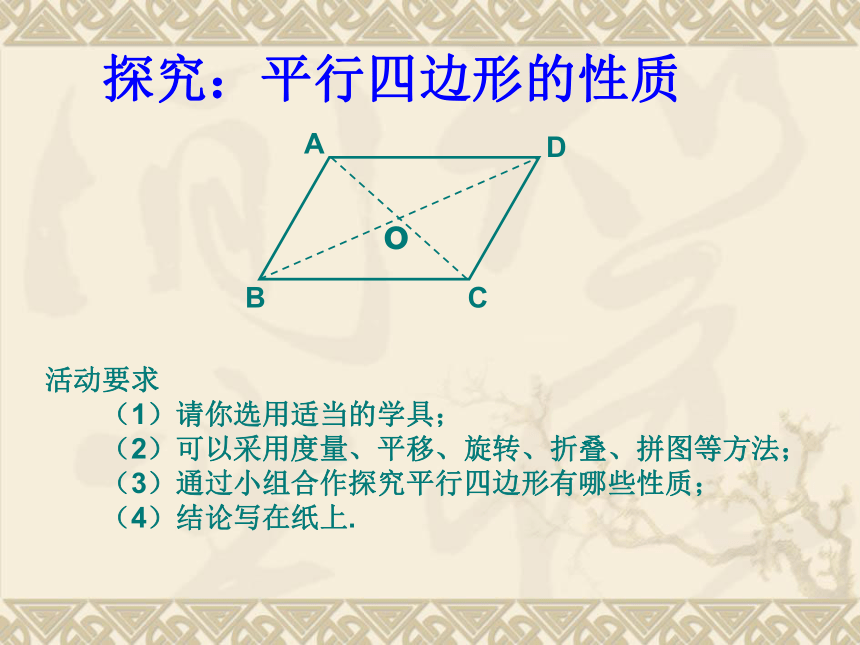
探究:平行四边形的性质
A
B
C
D
o
活动要求
(1)请你选用适当的学具;
(2)可以采用度量、平移、旋转、折叠、拼图等方法;
(3)通过小组合作探究平行四边形有哪些性质;
(4)结论写在纸上.
探究:平行四边形的性质
平行四边形的对边相等.
平行四边形的邻角互补.
平行四边形的对角相等.
平行四边形的对边平行.
平行四边形的对角线互相平分.
边:
角:
对角线:
绕对角线的交点旋转180度可以和原图形完全重合
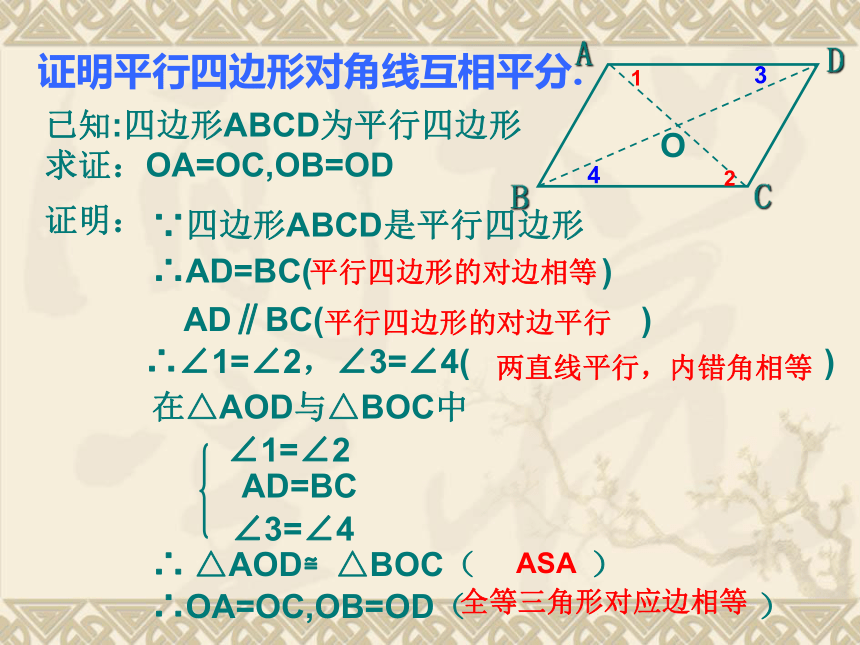
证明平行四边形对角线互相平分.
A
D
B
C
O
已知:四边形ABCD为平行四边形
求证:OA=OC,OB=OD
证明:
∵四边形ABCD是平行四边形
∴AD=BC( )
AD∥BC( )
∴∠1=∠2,∠3=∠4( )
1
2
3
4
在△AOD与△BOC中
∴ △AOD≌△BOC( )
∴OA=OC,OB=OD( )
平行四边形的对边相等
平行四边形的对边平行
两直线平行,内错角相等
∠1=∠2
AD=BC
∠3=∠4
ASA
全等三角形对应边相等
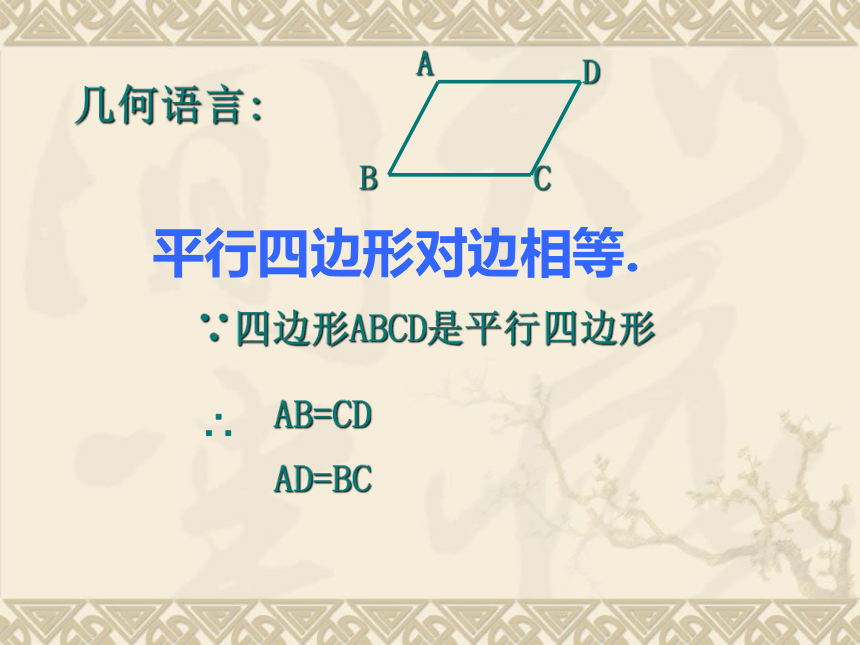
几何语言:
A
D
B
C
∵四边形ABCD是平行四边形
AB=CD
AD=BC
平行四边形对边相等.
∴
平行四边形对角相等.
∵四边形ABCD是平行四边形
∠A=∠C
∠B=∠D
∴
A
D
B
C
平行四边形邻角互补.
∵四边形ABCD是平行四边形
A
D
B
C
∠A+∠B=180O
∴
∠A+∠D=180O
∠C+∠B=180O
∠C+∠D=180O
平行四边形对角线互相平分.
∵四边形ABCD是平行四边形
AO=CO
BO=DO
∴
A
D
B
C
O
1 、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解:
四边形ABCD是平行四边形
思考探索
A
D
B
C
40
2.在 ABCD 中,AD=40,CD=30,
∠B=60°,则BC= ;AB= ;
∠A= , ∠C= , ∠D=
30
120°
120°
60°
思考探索
3、如下图 中,EF∥BC, GH∥AB, EF与GH相交于点O,则图中共有___个平行四边形.
ABCD
9
A
O
H
F
E
D
C
B
G
思考探索
4、如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是 .
O
D
B
A
C
●
1<AD<9
思考探索
拓展探究
把一个平行四边形的花池分成面积
相等的四部分,分别种不同颜色的花草,
你可以怎么分?
A
B
C
2.以点A、B、C为顶点建平行四边形的花池,你能找到第四个顶点D的位吗?D的位置有几种可能?
拓展探究
D1
D2
D3
A
B
C
D1
D2
D3
以点A、B、C为顶点画平行四边形,A的坐标为(1,2),
B的坐标为(0,0)C的坐标为(3,0),则第四个顶
点D的坐标可以为?
(4,2)
(-2,2)
(2,-2)
x
y
拓展延伸
小结
两组对边分别平行的四边形叫平行四边形
平行四边形的对边平行.
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的邻角互补.
平行四边形的对角线互相平分.
家庭作业:
再 见
观察下列图形
两组对边分别平行的四边形叫做平行四边形.
读作:平行四边形ABCD
A
D
B
C
记作: ABCD
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
两组对边分别平行
四边形
C
B
A
D
平行四边形
AB∥CD,AD ∥BC
观察思考
对边:AB与CD,AD与BC
对角:
对角线:AC、BD
C
B
D
A
你能从以下图形中找出平行四边形吗?
两组对边分别平行,是平行四边形的一个主要特征。
2
3
1
4
5
探究:平行四边形的性质
A
B
C
D
o
活动要求
(1)请你选用适当的学具;
(2)可以采用度量、平移、旋转、折叠、拼图等方法;
(3)通过小组合作探究平行四边形有哪些性质;
(4)结论写在纸上.
探究:平行四边形的性质
平行四边形的对边相等.
平行四边形的邻角互补.
平行四边形的对角相等.
平行四边形的对边平行.
平行四边形的对角线互相平分.
边:
角:
对角线:
绕对角线的交点旋转180度可以和原图形完全重合
证明平行四边形对角线互相平分.
A
D
B
C
O
已知:四边形ABCD为平行四边形
求证:OA=OC,OB=OD
证明:
∵四边形ABCD是平行四边形
∴AD=BC( )
AD∥BC( )
∴∠1=∠2,∠3=∠4( )
1
2
3
4
在△AOD与△BOC中
∴ △AOD≌△BOC( )
∴OA=OC,OB=OD( )
平行四边形的对边相等
平行四边形的对边平行
两直线平行,内错角相等
∠1=∠2
AD=BC
∠3=∠4
ASA
全等三角形对应边相等
几何语言:
A
D
B
C
∵四边形ABCD是平行四边形
AB=CD
AD=BC
平行四边形对边相等.
∴
平行四边形对角相等.
∵四边形ABCD是平行四边形
∠A=∠C
∠B=∠D
∴
A
D
B
C
平行四边形邻角互补.
∵四边形ABCD是平行四边形
A
D
B
C
∠A+∠B=180O
∴
∠A+∠D=180O
∠C+∠B=180O
∠C+∠D=180O
平行四边形对角线互相平分.
∵四边形ABCD是平行四边形
AO=CO
BO=DO
∴
A
D
B
C
O
1 、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
解:
四边形ABCD是平行四边形
思考探索
A
D
B
C
40
2.在 ABCD 中,AD=40,CD=30,
∠B=60°,则BC= ;AB= ;
∠A= , ∠C= , ∠D=
30
120°
120°
60°
思考探索
3、如下图 中,EF∥BC, GH∥AB, EF与GH相交于点O,则图中共有___个平行四边形.
ABCD
9
A
O
H
F
E
D
C
B
G
思考探索
4、如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是 .
O
D
B
A
C
●
1<AD<9
思考探索
拓展探究
把一个平行四边形的花池分成面积
相等的四部分,分别种不同颜色的花草,
你可以怎么分?
A
B
C
2.以点A、B、C为顶点建平行四边形的花池,你能找到第四个顶点D的位吗?D的位置有几种可能?
拓展探究
D1
D2
D3
A
B
C
D1
D2
D3
以点A、B、C为顶点画平行四边形,A的坐标为(1,2),
B的坐标为(0,0)C的坐标为(3,0),则第四个顶
点D的坐标可以为?
(4,2)
(-2,2)
(2,-2)
x
y
拓展延伸
小结
两组对边分别平行的四边形叫平行四边形
平行四边形的对边平行.
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的邻角互补.
平行四边形的对角线互相平分.
家庭作业:
再 见
