10.2 等腰三角形课件(共33张PPT)
文档属性
| 名称 | 10.2 等腰三角形课件(共33张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-03 18:59:50 | ||
图片预览






文档简介
第十章 三角形的有关证明
2 等腰三角形
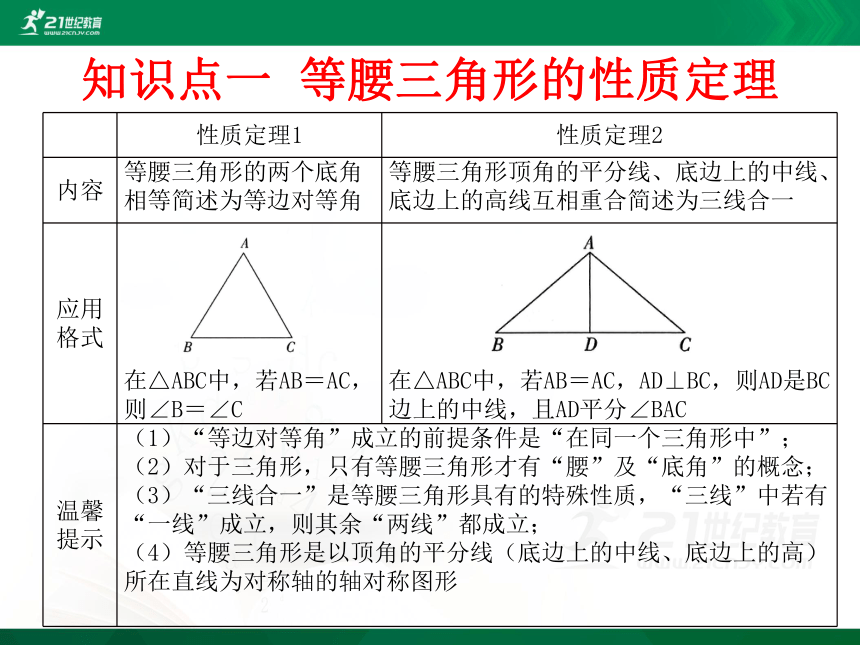
知识点一 等腰三角形的性质定理
性质定理1
性质定理2
内容
应用格式
温馨提示
知识点一 等腰三角形的性质定理
性质定理1
性质定理2
内容
等腰三角形的两个底角相等简述为等边对等角
等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合简述为三线合一
应用格式
在△ABC中,若AB=AC,则∠B=∠C
在△ABC中,若AB=AC,AD⊥BC,则AD是BC边上的中线,且AD平分∠BAC
温馨提示
(1)“等边对等角”成立的前提条件是“在同一个三角形中”;
(2)对于三角形,只有等腰三角形才有“腰”及“底角”的概念;
(3)“三线合一”是等腰三角形具有的特殊性质,“三线”中若有“一线”成立,则其余“两线”都成立;
(4)等腰三角形是以顶角的平分线(底边上的中线、底边上的高)所在直线为对称轴的轴对称图形
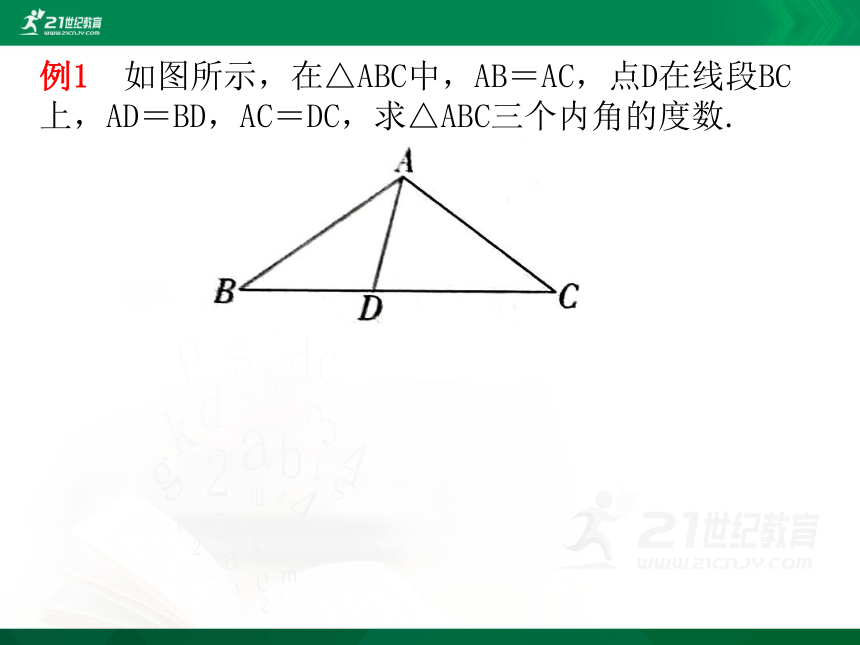
例1 如图所示,在△ABC中,AB=AC,点D在线段BC上,AD=BD,AC=DC,求△ABC三个内角的度数.
例1 如图所示,在△ABC中,AB=AC,点D在线段BC上,AD=BD,AC=DC,求△ABC三个内角的度数.
解析 ∵AC=DC,∴∠DAC=∠ADC,
又∵AB=AC,AD=BD,∴∠B=∠C=∠BAD,
设∠B=x,则∠ADC=∠B+∠BAD=2x,
∴∠DAC=∠ADC=2x,∴∠BAC=∠DAC+∠BAD=3x,∴在△ABC中,∠B+∠C+∠BAC=x+x+3x=180°,解得x=36°,
∴在△ABC中,∠BAC=108°,∠B=∠C=36°.
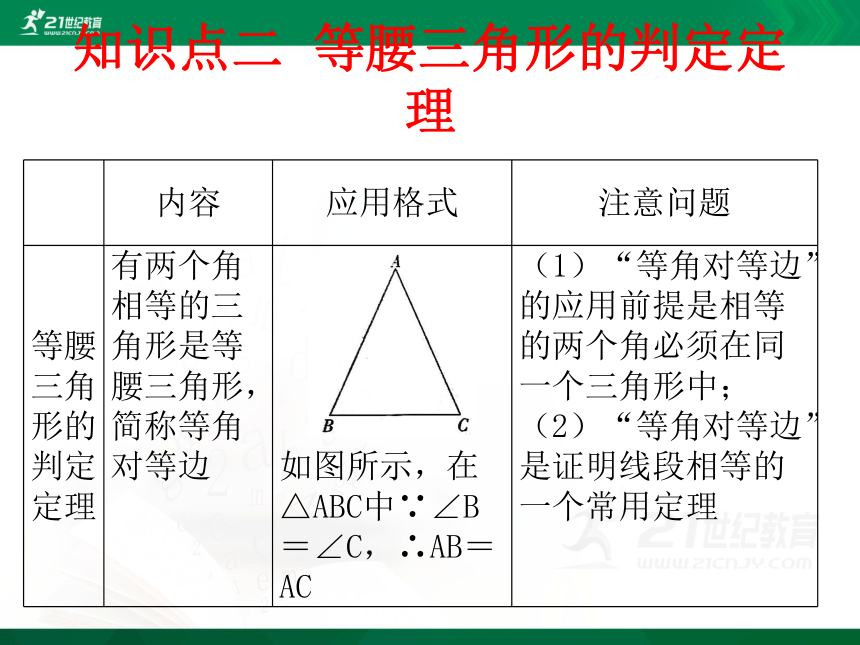
知识点二 等腰三角形的判定定理
内容
应用格式
注意问题
等腰三角形的判定定理
知识点二 等腰三角形的判定定理
内容
应用格式
注意问题
等腰三角形的判定定理
有两个角相等的三角形是等腰三角形,简称等角对等边
如图所示,在△ABC中∵∠B=∠C,∴AB=AC
(1)“等角对等边”的应用前提是相等的两个角必须在同一个三角形中;
(2)“等角对等边”是证明线段相等的一个常用定理
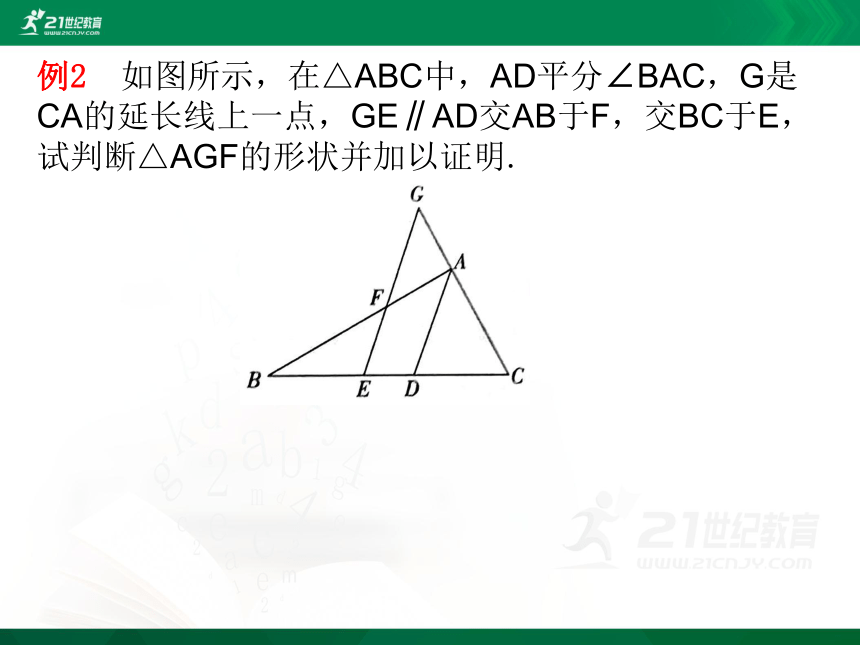
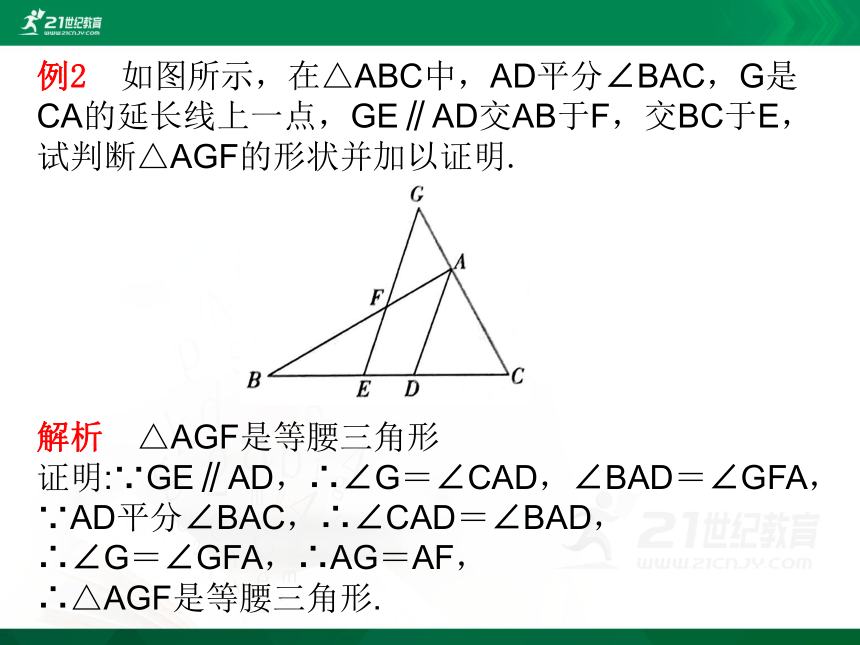
例2 如图所示,在△ABC中,AD平分∠BAC,G是CA的延长线上一点,GE∥AD交AB于F,交BC于E,试判断△AGF的形状并加以证明.
例2 如图所示,在△ABC中,AD平分∠BAC,G是CA的延长线上一点,GE∥AD交AB于F,交BC于E,试判断△AGF的形状并加以证明.
解析 △AGF是等腰三角形
证明:∵GE∥AD,∴∠G=∠CAD,∠BAD=∠GFA,
∵AD平分∠BAC,∴∠CAD=∠BAD,
∴∠G=∠GFA,∴AG=AF,
∴△AGF是等腰三角形.
知识点三 等边三角形的判定定理
内容
应用格式
等边三角形的判定定理
注意问题
知识点三 等边三角形的判定定理
内容
应用格式
等边三角形的判定定理
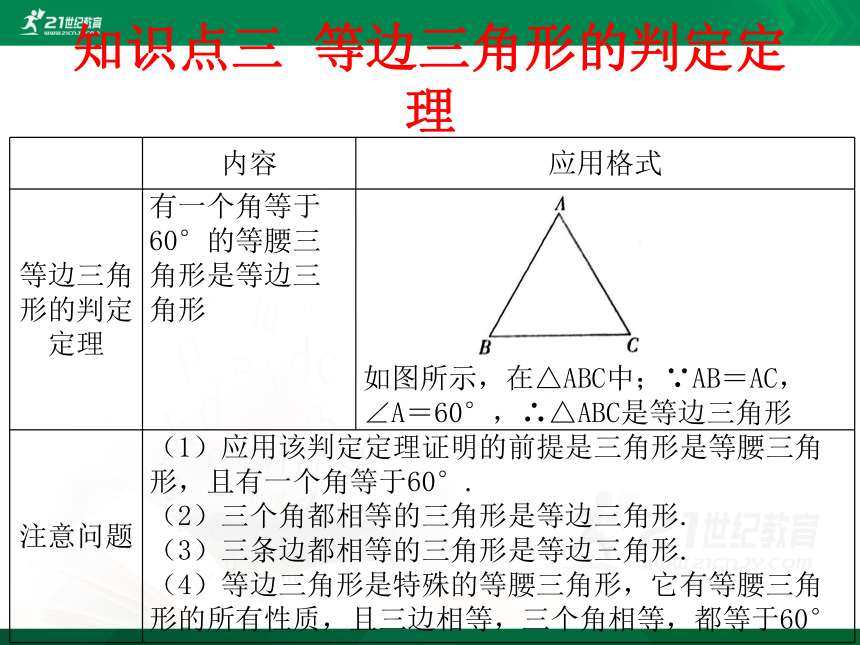
有一个角等于60°的等腰三角形是等边三角形
如图所示,在△ABC中;∵AB=AC,∠A=60°,∴△ABC是等边三角形
注意问题
(1)应用该判定定理证明的前提是三角形是等腰三角形,且有一个角等于60°.
(2)三个角都相等的三角形是等边三角形.
(3)三条边都相等的三角形是等边三角形.
(4)等边三角形是特殊的等腰三角形,它有等腰三角形的所有性质,且三边相等,三个角相等,都等于60°
例3 如图所示,已知△ABC是等边三角形,D为AC上任意一点,∠ABD=∠ACE,BD=CE.
求证:△ADE是等边三角形.
例3 如图所示,已知△ABC是等边三角形,D为AC上任意一点,∠ABD=∠ACE,BD=CE.
求证:△ADE是等边三角形.
证明:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),∴AD=AE,∠DAE=∠BAD=60°,∴△ADE是等边三角形.
知识点四 含30°角的直角三角形的性质
内容
应用格式
注意问题
含30°角的直角三角形的性质
知识点四 含30°角的直角三角形的性质
例4 如图所示,△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,求证:CD=2AD.
证明 在△ABC中,∵AB=AC,∠BAC=120°,∴∠B=∠C=30°,
又∵AD⊥AC,∴∠DAC=90°,
在Rt△DAC中∵∠C=30°,∴CD=2AD.
例4 如图所示,△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,求证:CD=2AD.
知识点五 反证法
项目
内容
概念
一般步骤
温馨 提示
知识点五 反证法
项目
内容
概念
先假设命题的结论不成立,然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定成立,这种证明方法称为反证法.反证法是一种重要的数学证明方法
一般步骤
(1)假设结论的反面是正确的;
(2)从假设出发,通过推理得出矛盾(与条件矛盾,与学过的定义、定理、公理矛盾,或自相矛盾);
(3)说明假设不成立,从而得到原命题结论正确
温馨 提示
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定
例5 证明:在一个三角形中,至少有一个内角小于或等于60度.
例5 证明:在一个三角形中,至少有一个内角小于或等于60度.
证明 假设在一个三角形中没有一个角小于或等于60°,即都大于60°,那么,这个三角形的三个内角之和就会大于180°,这与定理“三角形的三个内角之和等于180°”相矛盾,故假设不成立,所以在一个三角形中,至少有一个内角小于或等于60度.
经典例题
题型一 全等三角形的判定和性质的综合运用
例1 如图所示,已知在△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的平分线,且相交于O点.
(1)试说明△OBC是等腰三角形;
(2)连接OA,试判断直线OA与线段BC的关系,并说明理由.
(2)直线OA垂直平分线段BC.
理由:在△AOB和△AOC中,
∴△AOB≌△AOC(SSS),∴∠BAO=∠CAO,∴AO平分∠BAC,
∴直线OA垂直平分线段BC(等腰三角形顶角的平分线,底边上的高,底边上的中线互相重合).
题型二 等边三角形的判定和性质的综合应用
例2 如图所示,△ABC是等边三角形,DF⊥AB,DE⊥CB,EF⊥AC,求证:△DEF是等边三角形.
证明 ∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠ACB=∠CAB=60°.
∵DF⊥AB,DE⊥CB,EF⊥AC,
∴∠DAB=∠ACF=∠CBE=90°,
∴∠DBA=∠FAC=∠BCE=30°,
∴∠D=∠E=∠F=180°-90°-30°=60°,
∴△DEF是等边三角形.
点拨
要证三角形是等边三角形,可先证明这个三角形是等腰三角形,再证明三角形中任一内角为60°,或直接证明三角形的三个角或三条边都相等.
易错易混
易错点 作等腰三角形的高时易出错
当等腰三角形的顶角为钝角时,腰上的高在三角形的外部,这一点容易被忽略而导致出错.
例 若等腰三角形一腰上的高与另一腰的夹角是70°,则其底角为_________.
解析 ①如图1①∵∠ABD=70°,∠BDA=90°,
∴∠A=20°,∵AB=AC,
∴∠C=∠ABC=(180°-20°)÷2=80°.
②如图②,∵∠ABD=70°,∠BDA=90°,∴∠BAD=20°,
∵AB=AC,∴∠C=∠ABC=20°÷2=10°.
故答案为80°或10°.
答案 80°或10°
易错分析
本题易忽略腰上的高在三角形外部时的情况,导致漏解而出错.
2 等腰三角形
知识点一 等腰三角形的性质定理
性质定理1
性质定理2
内容
应用格式
温馨提示
知识点一 等腰三角形的性质定理
性质定理1
性质定理2
内容
等腰三角形的两个底角相等简述为等边对等角
等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合简述为三线合一
应用格式
在△ABC中,若AB=AC,则∠B=∠C
在△ABC中,若AB=AC,AD⊥BC,则AD是BC边上的中线,且AD平分∠BAC
温馨提示
(1)“等边对等角”成立的前提条件是“在同一个三角形中”;
(2)对于三角形,只有等腰三角形才有“腰”及“底角”的概念;
(3)“三线合一”是等腰三角形具有的特殊性质,“三线”中若有“一线”成立,则其余“两线”都成立;
(4)等腰三角形是以顶角的平分线(底边上的中线、底边上的高)所在直线为对称轴的轴对称图形
例1 如图所示,在△ABC中,AB=AC,点D在线段BC上,AD=BD,AC=DC,求△ABC三个内角的度数.
例1 如图所示,在△ABC中,AB=AC,点D在线段BC上,AD=BD,AC=DC,求△ABC三个内角的度数.
解析 ∵AC=DC,∴∠DAC=∠ADC,
又∵AB=AC,AD=BD,∴∠B=∠C=∠BAD,
设∠B=x,则∠ADC=∠B+∠BAD=2x,
∴∠DAC=∠ADC=2x,∴∠BAC=∠DAC+∠BAD=3x,∴在△ABC中,∠B+∠C+∠BAC=x+x+3x=180°,解得x=36°,
∴在△ABC中,∠BAC=108°,∠B=∠C=36°.
知识点二 等腰三角形的判定定理
内容
应用格式
注意问题
等腰三角形的判定定理
知识点二 等腰三角形的判定定理
内容
应用格式
注意问题
等腰三角形的判定定理
有两个角相等的三角形是等腰三角形,简称等角对等边
如图所示,在△ABC中∵∠B=∠C,∴AB=AC
(1)“等角对等边”的应用前提是相等的两个角必须在同一个三角形中;
(2)“等角对等边”是证明线段相等的一个常用定理
例2 如图所示,在△ABC中,AD平分∠BAC,G是CA的延长线上一点,GE∥AD交AB于F,交BC于E,试判断△AGF的形状并加以证明.
例2 如图所示,在△ABC中,AD平分∠BAC,G是CA的延长线上一点,GE∥AD交AB于F,交BC于E,试判断△AGF的形状并加以证明.
解析 △AGF是等腰三角形
证明:∵GE∥AD,∴∠G=∠CAD,∠BAD=∠GFA,
∵AD平分∠BAC,∴∠CAD=∠BAD,
∴∠G=∠GFA,∴AG=AF,
∴△AGF是等腰三角形.
知识点三 等边三角形的判定定理
内容
应用格式
等边三角形的判定定理
注意问题
知识点三 等边三角形的判定定理
内容
应用格式
等边三角形的判定定理
有一个角等于60°的等腰三角形是等边三角形
如图所示,在△ABC中;∵AB=AC,∠A=60°,∴△ABC是等边三角形
注意问题
(1)应用该判定定理证明的前提是三角形是等腰三角形,且有一个角等于60°.
(2)三个角都相等的三角形是等边三角形.
(3)三条边都相等的三角形是等边三角形.
(4)等边三角形是特殊的等腰三角形,它有等腰三角形的所有性质,且三边相等,三个角相等,都等于60°
例3 如图所示,已知△ABC是等边三角形,D为AC上任意一点,∠ABD=∠ACE,BD=CE.
求证:△ADE是等边三角形.
例3 如图所示,已知△ABC是等边三角形,D为AC上任意一点,∠ABD=∠ACE,BD=CE.
求证:△ADE是等边三角形.
证明:∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°.
在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),∴AD=AE,∠DAE=∠BAD=60°,∴△ADE是等边三角形.
知识点四 含30°角的直角三角形的性质
内容
应用格式
注意问题
含30°角的直角三角形的性质
知识点四 含30°角的直角三角形的性质
例4 如图所示,△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,求证:CD=2AD.
证明 在△ABC中,∵AB=AC,∠BAC=120°,∴∠B=∠C=30°,
又∵AD⊥AC,∴∠DAC=90°,
在Rt△DAC中∵∠C=30°,∴CD=2AD.
例4 如图所示,△ABC中,AB=AC,∠BAC=120°,AD⊥AC交BC于点D,求证:CD=2AD.
知识点五 反证法
项目
内容
概念
一般步骤
温馨 提示
知识点五 反证法
项目
内容
概念
先假设命题的结论不成立,然后推导出与定义、基本事实、已有定理或已知条件相矛盾的结果,从而证明命题的结论一定成立,这种证明方法称为反证法.反证法是一种重要的数学证明方法
一般步骤
(1)假设结论的反面是正确的;
(2)从假设出发,通过推理得出矛盾(与条件矛盾,与学过的定义、定理、公理矛盾,或自相矛盾);
(3)说明假设不成立,从而得到原命题结论正确
温馨 提示
在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定
例5 证明:在一个三角形中,至少有一个内角小于或等于60度.
例5 证明:在一个三角形中,至少有一个内角小于或等于60度.
证明 假设在一个三角形中没有一个角小于或等于60°,即都大于60°,那么,这个三角形的三个内角之和就会大于180°,这与定理“三角形的三个内角之和等于180°”相矛盾,故假设不成立,所以在一个三角形中,至少有一个内角小于或等于60度.
经典例题
题型一 全等三角形的判定和性质的综合运用
例1 如图所示,已知在△ABC中,AB=AC,BD和CE分别是∠ABC和∠ACB的平分线,且相交于O点.
(1)试说明△OBC是等腰三角形;
(2)连接OA,试判断直线OA与线段BC的关系,并说明理由.
(2)直线OA垂直平分线段BC.
理由:在△AOB和△AOC中,
∴△AOB≌△AOC(SSS),∴∠BAO=∠CAO,∴AO平分∠BAC,
∴直线OA垂直平分线段BC(等腰三角形顶角的平分线,底边上的高,底边上的中线互相重合).
题型二 等边三角形的判定和性质的综合应用
例2 如图所示,△ABC是等边三角形,DF⊥AB,DE⊥CB,EF⊥AC,求证:△DEF是等边三角形.
证明 ∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠ACB=∠CAB=60°.
∵DF⊥AB,DE⊥CB,EF⊥AC,
∴∠DAB=∠ACF=∠CBE=90°,
∴∠DBA=∠FAC=∠BCE=30°,
∴∠D=∠E=∠F=180°-90°-30°=60°,
∴△DEF是等边三角形.
点拨
要证三角形是等边三角形,可先证明这个三角形是等腰三角形,再证明三角形中任一内角为60°,或直接证明三角形的三个角或三条边都相等.
易错易混
易错点 作等腰三角形的高时易出错
当等腰三角形的顶角为钝角时,腰上的高在三角形的外部,这一点容易被忽略而导致出错.
例 若等腰三角形一腰上的高与另一腰的夹角是70°,则其底角为_________.
解析 ①如图1①∵∠ABD=70°,∠BDA=90°,
∴∠A=20°,∵AB=AC,
∴∠C=∠ABC=(180°-20°)÷2=80°.
②如图②,∵∠ABD=70°,∠BDA=90°,∴∠BAD=20°,
∵AB=AC,∴∠C=∠ABC=20°÷2=10°.
故答案为80°或10°.
答案 80°或10°
易错分析
本题易忽略腰上的高在三角形外部时的情况,导致漏解而出错.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
