七年级数学下册试题: 第五章《生活中的轴对称》习题-北师大版(Word版 含答案)
文档属性
| 名称 | 七年级数学下册试题: 第五章《生活中的轴对称》习题-北师大版(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 392.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 18:16:52 | ||
图片预览



文档简介
《生活中的轴对称》习题
一、选择题
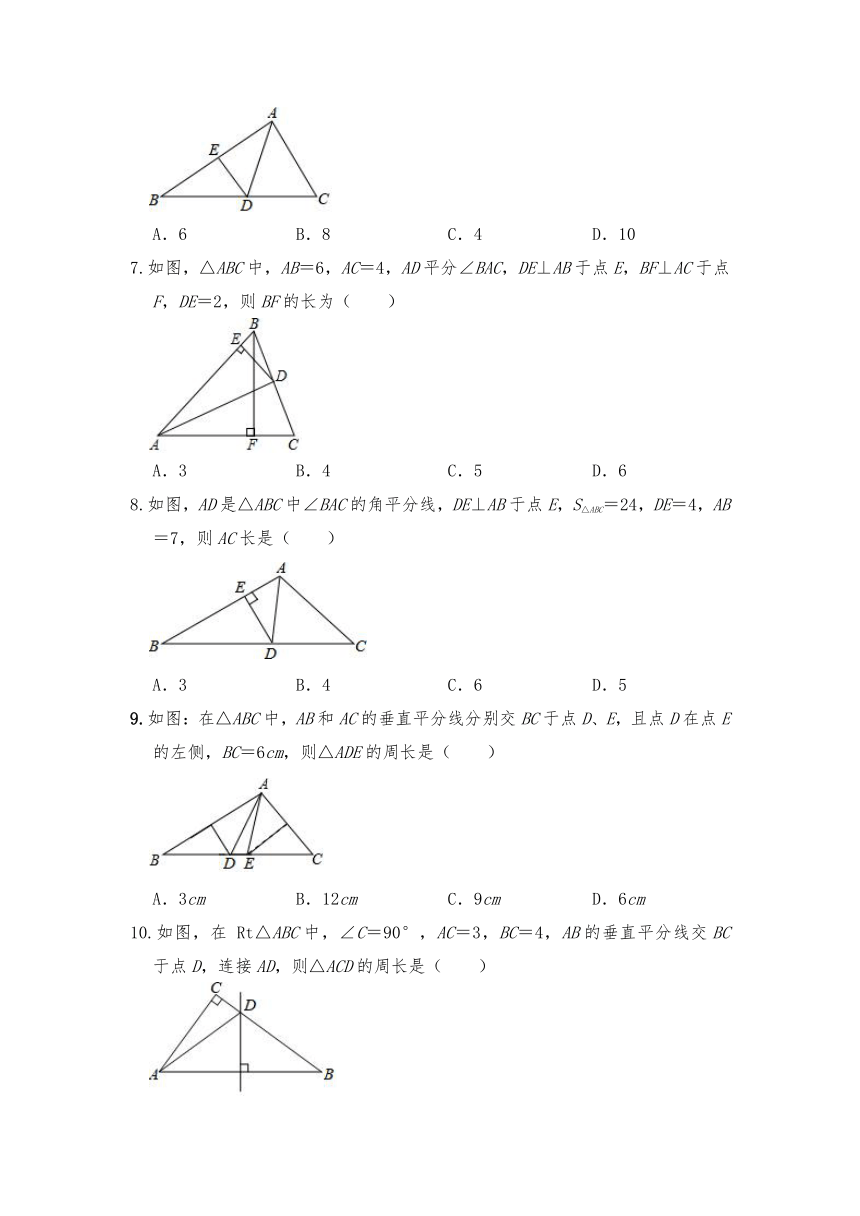
1.下列图形中,不是轴对称图形的是( )
A.
B.
C.
D.
2.如图,四个手机应用图标中是轴对称图形的是( )
A.
B.
C.
D.
3.下列四个图形中,不是轴对称图形的是( )
A.
B.
C.
D.
4.下列图形中,不是轴对称图形的有( )
A.1个
B.2个
C.3个
D.4个
5.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,若AB=6cm,则△DBE的周长是( )
A.6
cm
B.7
cm
C.8
cm
D.9
cm
6.如图,AD是△ABC的角平分线,DE⊥AB于E,已知△ABC的面积为28.AC=6,DE=4,则AB的长为( )
A.6
B.8
C.4
D.10
7.如图,△ABC中,AB=6,AC=4,AD平分∠BAC,DE⊥AB于点E,BF⊥AC于点F,DE=2,则BF的长为( )
A.3
B.4
C.5
D.6
8.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=24,DE=4,AB=7,则AC长是( )
A.3
B.4
C.6
D.5
9.如图:在△ABC中,AB和AC的垂直平分线分别交BC于点D、E,且点D在点E的左侧,BC=6cm,则△ADE的周长是( )
A.3cm
B.12cm
C.9cm
D.6cm
10.如图,在
Rt△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交BC于点D,连接AD,则△ACD的周长是( )
A.7
B.8
C.9
D.10
11.如图,在△ABC中,点E在边AC上,DE是AB的垂直平分线,△ABC的周长为19,△BCE的周长为12,则线段AB的长为( )
A.9
B.8
C.7
D.6
12.如图,在△ABC中,PM、QN分别是AB、AC的垂直平分线,∠BAC=100°那么∠PAQ等于( )
A.50°
B.40°
C.30°
D.20°
13.已知等腰三角形一腰的垂直平分线与另一腰所在的直线的夹角为40°,则此等腰三角形的顶角是( )
A.50°
B.130°
C.50°或
140°
D.50°或
130°
14.如图,已知AB=AC=BD,则∠1与∠2的关系是( )
A.3∠1﹣∠2=180°
B.2∠1+∠2=180°
C.∠1+3∠2=180°
D.∠1=2∠2
15.如图,若AB=AC,下列三角形能被一条直线分成两个小等腰三角形的是( )
A.(1)(2)(3)
B.(1)(3)(4)
C.(2)(3)(4)
D.(1)(2)(4)
16.如图,在第一个△ABA1中∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法进行下去,则以点A4为顶点的等腰三角形的底角的度数为( )
A.175°
B.170°
C.10°
D.5°
二、解答题
1.如图是网格中由五个小正方形组成的图形,根据下列要求画图(涂上阴影)
(1)图①中,添加一块小正方形,使之成为轴对称图形,且有两条对称轴;
(2)图②中,添加一块小正方形,使之成为轴对称图形,且只有一条对称轴(画出一个即可)
2.如图,下列4×4网格图都是由16个相间小正方形组成,每个网格图中有4个小正方形已涂上阴影,在空白小正方形中,选取2个涂上阴影,使6个阴影小正方形组成个轴对称图形,请设计出四种方案.
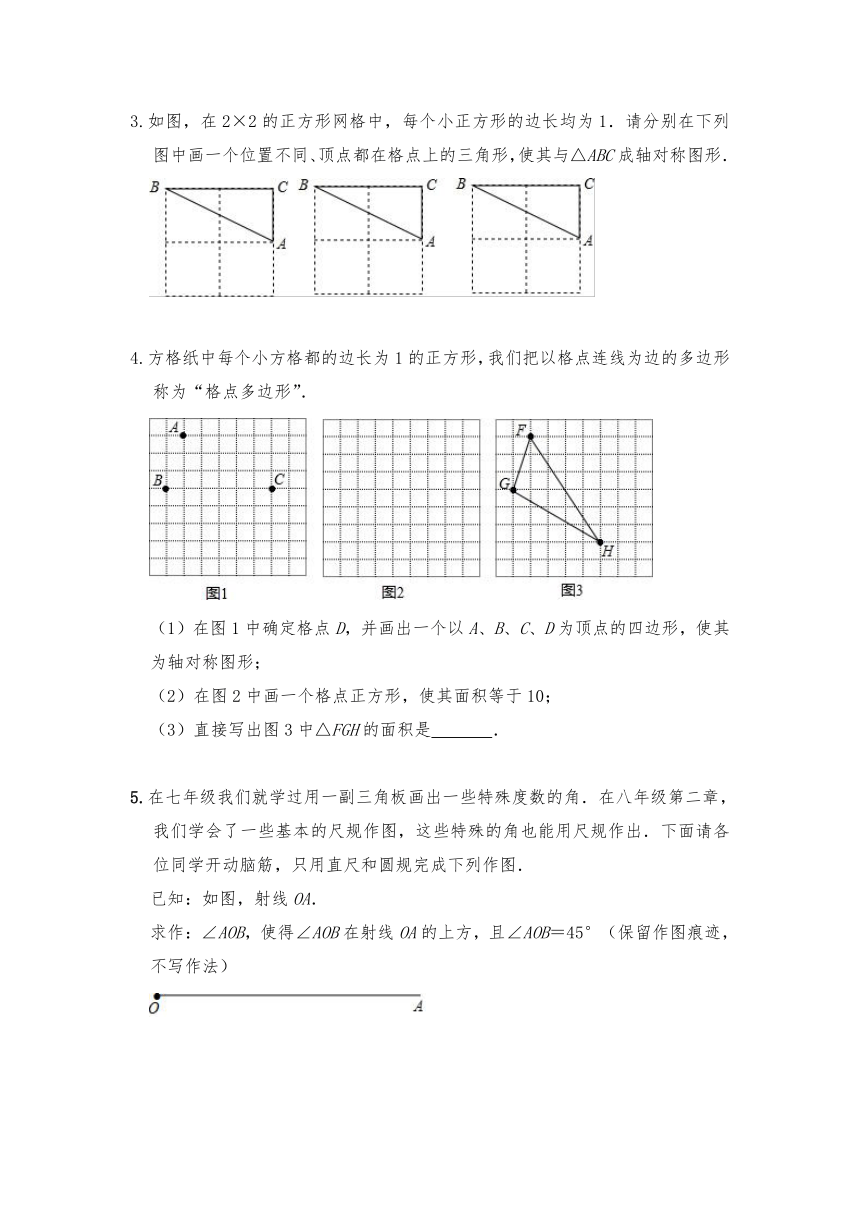
3.如图,在2×2的正方形网格中,每个小正方形的边长均为1.请分别在下列图中画一个位置不同、顶点都在格点上的三角形,使其与△ABC成轴对称图形.
4.方格纸中每个小方格都的边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.
(1)在图1中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其为轴对称图形;
(2)在图2中画一个格点正方形,使其面积等于10;
(3)直接写出图3中△FGH的面积是
.
5.在七年级我们就学过用一副三角板画出一些特殊度数的角.在八年级第二章,我们学会了一些基本的尺规作图,这些特殊的角也能用尺规作出.下面请各位同学开动脑筋,只用直尺和圆规完成下列作图.
已知:如图,射线OA.
求作:∠AOB,使得∠AOB在射线OA的上方,且∠AOB=45°(保留作图痕迹,不写作法)
6.已知:如图,在△ABC中,AC<AB且∠C=2∠B
(1)用直尺和圆规作出一条过点A的直线1,使得点C关于直线的对称点落在边AB上(不写作法,保留作图痕迹)
(2)设(1)中直线l与边BC的交点为D,请写出线段AB、AC、CD之间的数量关系并说明理由.
7.如图,△ABC中,AB=3,AC=4,BC=5.
(1)试用直尺和圆规,在直线AB上求作点P,使△PBC为等腰三角形.要求:①保留作图痕迹;②若点P有多解,则应作出所有的点P,并在图中依次标注P1、P2、P3、…;
(2)根据(1)求PA的长(所有可能的值)
8.如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长.
9.茅坪民族中学八(2)班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,站在C处的学生小明先拿桔子再拿糖果,然后回到C处,请你在下图帮助他设计一条行走路线,使其所走的总路程最短?
10.如图,为了做好元旦期间的交通安全工作,自贡市交警执勤小队从A处出发,先到公路m上设卡检査,再到公路n上设卡检査,最后再到达B地执行任务,他们应如何走才能使总路程最短?画出图形并说明做法.
11.如图,点P是∠AOB内部一点,现有一只蚂蚁要从P的出发,先到OA,再到OB,最后返回到点P.请作出蚂蚁爬行的最短路径(要求:保留作图痕迹,不写作法.)
12.如图直线l1,l2表示一条河的两岸,且l1∥l2,现要在这条河上建一座桥.桥建在何处才能使从村庄A经过河到村庄B的路线最短?画出示意图,并说明理由.
13.在△ABC中,∠BAC=a,点D,点E在BC上,连接AD,AE.
(1)如图,若a=120°,BA=BE,CA=CD,求∠DAE的度数;
(2)若DA=DB,EA=EC,直接写出∠DAE=
(用a的式子表示).
14.如图,△ABC中,AE=BE,∠AED=∠ABC.
(1)求证:BD平分∠ABC;
(2)若AB=CB,∠AED=4∠EAD,求∠C的度数.
15.已知:在△ABC中,∠B=∠C,D,E分别是线段BC,AC上的一点,且AD=AE,
(1)如图1,若∠BAC=90°,D是BC中点,则∠2的度数为
;
(2)借助图2探究并直接写出∠1和∠2的数量关系
.
16.数学课上,张老师举了下面的例题:
例1等腰三角形ABC中,∠A=110°,求∠B的度数.(答案:35°)
例2等腰三角形ABC中,∠A=40°,求∠B的度数.(答案:40°或70°或100°)
张老师启发同学们进行变式,小敏编了如下两题:
变式1:等腰三角形ABC中,∠A=100°,求∠B的度数.
变式2:等腰三角形ABC中,∠A=45°,求∠B的度数.
(1)请你解答以上两道变式题.
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同.如果在等腰三角形ABC中,设∠A=x°,当∠B只有一个度数时,请你探索x的取值范围.
17.在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
(1)如图1,连接BE、CE,则BE=CE吗?说明理由;
(2)若∠BAC=45°,BE的延长线与AC垂直相交于点F时,如图2,BD=AE吗?说明理由.
18.如图,等腰△ABC,点D、E、F分别在BC、AB、AC上,且∠BAC=∠ADE=∠ADF=60°.
(1)在图中找出与∠DAC相等的角,并加以证明;
(2)若AB=6,BE=m,求:AF(用含m的式子表示).
19.如图,在△ABC中,AB=AC,∠BAC=100°,BD平分∠ABC,且BD=AB,连接AD、DC.
(1)求证:∠CAD=∠DBC;
(2)求∠BDC的度数.
20.在△ABC和△DCE中,CA=CB,CD=CE,∠CAB=∠CED=α.
(1)如图1,将AD、EB延长,延长线相交于点O:
①求证:BE=AD;
②用含α的式子表示∠AOB的度数(直接写出结果);
(2)如图2,当α=45°时,连接BD、AE,作CM⊥AE于M点,延长MC与BD交于点N,求证:N是BD的中点.
21.△ABC,直线DE交AB于D,交AC于E,将△ADE沿DE折叠,使A落在同一平面上的A′处,∠A′的两边与BD、CE的夹角分别记为∠1,∠2.
(1)如图①,当A′落在四边形BDEC内部时,探索∠A与∠1+∠2之间的数量关系,并说明理由.
(2)如图②,当A′落在AC右侧时,探索∠A与∠1,∠2之间的数量关系,并说明理由.
22.如图(1),△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点,
研究(1):如果沿直线DE折叠,则∠BDA′与∠A的关系是
.
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.
23.图形在折叠过程中会形成相等的边和相等的角,下面是同学们在数学课上所做的三角形、四边形折叠实验,请根据实验过程解决问题:
问题(一)
如图①,一张三角形ABC纸片,点D、E分别是△ABC边上两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′和∠A的数量关系是
;
研究(2):如果折成图②的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是
;
研究(3):如果折成图③的形状,猜想∠BDA′、∠CEA′和∠A的数量关系,并说明理由.
问题(二)
研究(4):将问题(一)推广,如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是
.(直接写出结论)
24.发现(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,请你判断∠1+∠2与∠A有何数量关系,直接写出你的结论,不必说明理由
思考(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=100°,求∠BIC的度数;
拓展(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
答案
一、选择题
1.B.2.D.3.C.4.A.5.A.6.B7.C.8.D.
9.D.10.A.11.C.12.D.13.D.14.A.15.B.16.D.
二、解答题
1.解:(1)如图①所示:即为所求;
(2)如图②所示:即为所求.
2.解:如图所示:
3.画对任意三种即可.
.
4.解:(1)如图1所示:
(2)如图2所示:
(3)如图3所示:
△FGH的面积=矩形ABHC的面积﹣△AFG的面积﹣△BGH的面积﹣△FCH的面积
=5×6﹣﹣﹣
=9
故答案为:9.
5.解:如图所示,∠AOB即为所作.
6.解:(1)如图所示,直线AD即为所求;
(2)线段AB、AC、CD之间的数量关系为:AB=AC+CD.
理由:由题可得,AE=AC,∠CAD=∠EAD,AD=AD,
∴△ACD≌△AED(SAS),
∴DE=CD,∠AED=∠C=2∠B,
又∵∠AED=∠B+∠BDE,
∴∠B=∠BDE,
∴BE=DE=CD,
又∵AB=AE+BE,
∴AB=AC+CD.
7.解:(1)如图,点P1、P2、P3、P4为所作;
(2)∵AB=3,AC=4,BC=5.
∴AB2+AC2=BC2,
∴△ABC为直角三角形,∠BAC=90°,
当CP1=CB时,
∵CA⊥BP1,
∴AP1=AB=3;
当BP2=BP3=BC=5时,
AP2=AB+BP2=3+5=8;
AP3=BP3﹣AB=5﹣3=2;
当P4C=P4B时,
设AP4=x,则P4C=P4B=x+3,
在Rt△P4AC中,x2+42=(x+3)2,解得x=,
即AP4=.
综上所述,AP的值可能为2、3、8、.
8.解:(1)如图,作AB的垂直平分线,交BC于点P,则点P即为所求;
(2)如图,①在BC上取点D,过点D作BC的垂线,②在垂线上取点E使DE=DB,连接EC,③作EC的垂直平分线交BC于点F;
∴Rt△DEF即为所求.
9.解:①分别作点C关于OA、OB的对称点是M、N,
②连接MN,分别交OA于D,OB于E.
则C→D→E→C为所求的行走路线.
10.解:如图所示,分别作A、B关于公路m、n的对称点A′、B′,连接A′B′交m、n于M、N两点,连AM、BN,则A→M→N→B即为最短路线.
11.解:如图,
作点P关于OA、OB的对称点P′、P″,
连接P′P″与OA、OB交于点M、N,
则蚂蚁爬行的最短路径为:
PM+MN+PN=P′M+MN+P″N=P′P″.
12.解:如图,先确定AA′与河等宽,且AA′⊥河岸,连接BA′,与河岸的交点就是点C,过点C作CD垂直河岸,交另一河岸于点D,CD就是所求的桥的位置.
理由:由作图过程可知,四边形ACDA′为平行四边形,AD平移至A′C即可得到线段A′B,两点之间,线段最短,由于河宽不变,CD即为桥.
13.解:(1)∵BE=BA,
∴∠BAE=∠BEA,
∴∠B=180°﹣2∠BAE,①
∵CD=CA,
∴∠CAD=∠CDA,
∴∠C=180°﹣2∠CAD,②
①+②得:∠B+∠C=360°﹣2(∠BAE+∠CAD)
∴180°﹣∠BAC=360°﹣2[(∠BAD+∠DAE)+(∠DAE+∠CAE)],
∴﹣∠BAC=180°﹣2[(∠BAD+∠DAE+∠CAE)+∠DAE],
∴﹣∠BAC=180°﹣2(∠BAC+∠DAE),
∴2∠DAE=180°﹣∠BAC.
∵∠BAC=120°,
∴2∠DAE=180°﹣120°=60°,
∴∠DAE=30°,
(2)∵DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
又在△ABC中,∠B+∠C=180°﹣∠BAC=180°﹣α,
∴∠DAB+∠EAC=∠B+∠C=70°,
∴∠DAE=∠BAC﹣(∠DAB+∠EAC)
=α﹣(180°﹣α)=2α﹣180°.
故答案为:2α﹣180°.
14.(1)证明:∵∠AED=∠ABC,∠AED=∠ABE+∠EAB,∠ABC=∠ABE+∠DBC,
∴∠EAB=∠DBC,
∵AE=BE,
∴∠EAB=∠ABE,
∴∠DBC=∠ABE,
∴BD平分∠ABC;
(2)设∠EAD=x,则∠AED=4x,
∵∠AED=∠ABE+∠EAB,∠EAB=∠ABE,BD平分∠ABC,
∴∠BAE=2x,∠ABC=4x,
∴∠BAC=3x,
∵AB=CB,
∴∠BAC=∠C,
∴∠C=3x,
∵∠ABC+∠BAC+∠C﹣180°,
∴4x+3x+3x=180°,
解得,x=18°,
∴∠C=3x=54°,
即∠C的度数是54°.
15.解:(1)∠AED=∠CDE+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,
∴∠AED=∠ADE,
∵∠B=∠C,∠BAC=90°,D是BC中点,
∴∠BAD=45°,
∴∠B+∠BAD=∠EDC+∠C+∠CDE,
即∠BAD=2∠CDE,
∴∠2=22.5°;
(2)∠AED=∠CDE+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,
∴∠AED=∠ADE,
∵AB=AC,
∴∠B=∠C,
∴∠B+∠BAD=∠EDC+∠C+∠CDE,
即∠BAD=2∠CDE,∠1=2∠2.
16.解:(1)变式1:∵∠A=100°,
∴∠A只能为△ABC的顶角,
∵△ABC为等腰三角形,
∴∠B=∠C=×(180°﹣100°)=40°;
变式2:若∠A为顶角,则∠B=(180°﹣∠A)÷2=67.5°;
若∠A为底角,∠B为顶角,则∠B=180°﹣2×45°=90°;
若∠A为底角,∠B为底角,则∠B=45°;
故∠B=67.5°或90°或45°;
(2)分两种情况:
①当90≤x<180时,∠A只能为顶角,
∴∠B的度数只有一个;
②当0<x<90时,当x=60时,等腰三角形ABC是等边三角形,
∴∠B的度数只有一个,
∴当∠B只有一个度数时,请你探索x的取值范围为90≤x<180或60.
17.解:(1)成立.
理由:∵AB=AC,D是BC的中点,
∴∠BAE=∠CAE.
在△ABE和△ACE中,,
∴△ABE≌△ACE(SAS),
∴BE=CE;
(2)成立.
理由:∵∠BAC=45°,BF⊥AF.
∴△ABF为等腰直角三角形
∴AF=BF,
由(1)知AD⊥BC,
∴∠EAF=∠CBF
在△AEF和△BCF中,,
∴△AEF≌△BCF(ASA),
∴AE=BC,
∵BD=BC,
∴BD=AE.
18.解:(1)结论:∠BDE=∠DAC.
理由:∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∴∠C=60°,
∵∠ADB=∠3+∠ADE=∠1+∠C,∠ADE=∠C=60°,
∴∠3=∠1.
(2)如图,在DE上截取DG=DF,连接AG,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠ADE=∠ADF=60°,AD=AD,
∴△ADG≌△ADF(SAS),
∴AG=AF,∠1=∠2,
∵∠3=∠1,
∴∠3=∠2
∵∠AEG=60°+∠3,∠AGE=60°+∠2,
∴∠AEG=∠AGE,
∴AE=AG,
∴AE=AF=6﹣m.
19.证明(1)∵AB=AC,∠BAC=100°
∴∠ABC=∠ACB=40°
∵BD平分∠ABC
∴∠ABD=∠DBC=20°
∵BD=AB
∴∠ADB=∠DAB=80°
∴∠CAD=20°
∴∠CAD=∠DBC
(2)延长AD到点E,使得AE=BC,
∵BD=AB=AC,∠CAD=∠DBC,
∴△DBC≌△CAE,
∴CD=CE,∠BDC=∠ACE,
∴∠CDE=∠CED=α,
∵∠ADB=80°,
∴∠BDE=100°
∴∠BDC=∠ACE=100°+α,
∴20°+100°+α+α=180°,
∴α=30°,
∴∠BDC=130°.
20.解:(1)①∵CA=CB,CD=CE,∠CAB=∠CED=α,
∴∠ACB=180°﹣2α,∠DCE=180°﹣2α,
∴∠ACB=∠DCE,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,,
∴△ACD≌△BCE(SAS),
∴BE=AD;
②∵△ACD≌△BCE,
∴∠CAD=∠CBE=α+∠BAO,
∵∠ABE=∠BOA+∠BAO,
∴∠CBE+α=∠BOA+∠BAO,
∴∠BAO+α+α=∠BOA+∠BAO,
∴∠BOA=2α;
(2)如图2,作BP⊥MN交MN的延长线于P,作DQ⊥MN于Q,
∵∠BCP+∠BCA=∠CAM+∠AMC,
∵∠BCA=∠AMC,
∴∠BCP=∠CAM,
在△CBP与△ACM中,,
∴△CBP≌△ACM(AAS),
∴MC=BP,
同理,CM=DQ,
∴DQ=BP,
在△BPN与△DQN中,,
∴△BPN≌△DQN(AAS),
∴BN=ND,
∴N是BD的中点.
21.解:(1)2∠A=∠1+∠2.理由如下:
如图①.∵∠A+∠A′+∠AEA′+∠ADA′=360°,
又∵∠1+∠ADA′+∠2+∠AEA′=360°,
∴∠A+∠A′=∠1+∠2,
又∵∠A=∠A′,
∴2∠A=∠1+∠2;
(2)2∠A=∠1﹣∠2.理由如下:
如图②,设DA′交AC于点F.
∵∠1=∠A+∠DFA,∠DFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2,
∴∠A+∠A′=∠1﹣∠2,
∵△A′DE是由△ADE沿直线DE折叠而得,
∴∠A=∠A′,
∴2∠A=∠1﹣∠2.
22.解:(1)∠BDA′=2∠A;
故答案为:∠BDA′=2∠A;
(2)∠BDA′+∠CEA′=2∠A,
理由:在四边形ADA′E中,∠A+∠DA′E+∠ADA′+∠A′EA=360°
∴∠A+∠DA′E=360°﹣∠ADA′﹣∠A′EA
∵∠BDA′+∠ADA′=180°,∠CEA′+∠A′EA=180°
∴∠BDA′+∠CEA′=360°﹣∠ADA′﹣∠A′EA
∴∠BDA′+∠CEA′=∠A+∠DA′E
∵△A′DE是由△ADE沿直线DE折叠而得
∴∠A=∠DA′E
∴∠BDA′+∠CEA′=2∠A;
(3)∠BDA′﹣∠CEA′=2∠A
理由:DA′交AC于点F,
∵∠BDA′=∠A+∠DFA,∠DFA=∠A′+∠CEA′
∴∠BDA′=∠A+∠A′+∠CEA′
∴∠BDA′﹣∠CEA′=∠A+∠A′
∵△A′DE是由△ADE沿直线DE折叠而得
∴∠A=∠DA′E
∴∠BDA′﹣∠CEA′=2∠A.
23.解:(1)∵根据折叠的性质可知∠DA′E=∠A,∠DA′E+∠A=∠BDA′,
′∴∠BDA=2∠A.
故答案为:∠BDA=2∠A;
(2)由图形折叠的性质可知,∠CEA′=180°﹣2∠DEA′…①,∠BDA′=180°﹣2∠A′DE…②,
①+②得,∠BDA′+∠CEA′=360°﹣2(∠DEA′+∠A′DE
即∠BDA′+∠CEA′=360°﹣2(180°﹣∠A),
故∠BDA′+∠CEA′=2∠A.
故答案为:∠BDA′+∠CEA′=2∠A;
(3)∠BDA′﹣∠CEA′=2∠A.
证明如下:
连接AA′构造等腰三角形,
∠BDA′=2∠DA'A,∠CEA'=2∠EA'A,
得∠BDA'﹣∠CEA'=2∠A,
(4)如图④,由图形折叠的性质可知∠1=180°﹣2∠AEF,∠2=180°﹣2∠BFE,
两式相加得,∠1+∠2=360°﹣2(∠AEF+∠BFE)
即∠1+∠2=360°﹣2(360°﹣∠A﹣∠B),
所以,∠1+∠2=2(∠A+∠B)﹣360°.
故答案为:∠1+∠2=2(∠A+∠B)﹣360°.
24.解:(1)∠1+∠2=2∠A;
理由:根据翻折的性质,∠ADE=(180°﹣∠1),∠AED=(180°﹣∠2),
∵∠A+∠ADE+∠AED=180°,
∴∠A+(180﹣∠1)+(180﹣∠2)=180°,
整理得2∠A=∠1+∠2;
(2)由(1)∠1+∠2=2∠A,得2∠A=100°,
∴∠A=50°
∵IB平分∠ABC,IC平分∠ACB,
∴∠IBC+∠ICB=(∠ABC+∠ACB)=(180°﹣∠A)=90°﹣∠A,
∴∠BIC=180°﹣(∠IBC+∠ICB)=180°﹣(90°﹣∠A)=90°+×50°=115°;
(3)∵BF⊥AC,CG⊥AB,
∴∠AFH+∠AGH=90°+90°=180°,
∠FHG+∠A=180°,
∴∠BHC=∠FHG=180°﹣∠A,
由(1)知∠1+∠2=2∠A,
∴∠A=(∠1+∠2),
∴∠BHC=180°﹣(∠1+∠2).
一、选择题
1.下列图形中,不是轴对称图形的是( )
A.
B.
C.
D.
2.如图,四个手机应用图标中是轴对称图形的是( )
A.
B.
C.
D.
3.下列四个图形中,不是轴对称图形的是( )
A.
B.
C.
D.
4.下列图形中,不是轴对称图形的有( )
A.1个
B.2个
C.3个
D.4个
5.如图,在△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,若AB=6cm,则△DBE的周长是( )
A.6
cm
B.7
cm
C.8
cm
D.9
cm
6.如图,AD是△ABC的角平分线,DE⊥AB于E,已知△ABC的面积为28.AC=6,DE=4,则AB的长为( )
A.6
B.8
C.4
D.10
7.如图,△ABC中,AB=6,AC=4,AD平分∠BAC,DE⊥AB于点E,BF⊥AC于点F,DE=2,则BF的长为( )
A.3
B.4
C.5
D.6
8.如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=24,DE=4,AB=7,则AC长是( )
A.3
B.4
C.6
D.5
9.如图:在△ABC中,AB和AC的垂直平分线分别交BC于点D、E,且点D在点E的左侧,BC=6cm,则△ADE的周长是( )
A.3cm
B.12cm
C.9cm
D.6cm
10.如图,在
Rt△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交BC于点D,连接AD,则△ACD的周长是( )
A.7
B.8
C.9
D.10
11.如图,在△ABC中,点E在边AC上,DE是AB的垂直平分线,△ABC的周长为19,△BCE的周长为12,则线段AB的长为( )
A.9
B.8
C.7
D.6
12.如图,在△ABC中,PM、QN分别是AB、AC的垂直平分线,∠BAC=100°那么∠PAQ等于( )
A.50°
B.40°
C.30°
D.20°
13.已知等腰三角形一腰的垂直平分线与另一腰所在的直线的夹角为40°,则此等腰三角形的顶角是( )
A.50°
B.130°
C.50°或
140°
D.50°或
130°
14.如图,已知AB=AC=BD,则∠1与∠2的关系是( )
A.3∠1﹣∠2=180°
B.2∠1+∠2=180°
C.∠1+3∠2=180°
D.∠1=2∠2
15.如图,若AB=AC,下列三角形能被一条直线分成两个小等腰三角形的是( )
A.(1)(2)(3)
B.(1)(3)(4)
C.(2)(3)(4)
D.(1)(2)(4)
16.如图,在第一个△ABA1中∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C,得到第二个△A1A2C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法进行下去,则以点A4为顶点的等腰三角形的底角的度数为( )
A.175°
B.170°
C.10°
D.5°
二、解答题
1.如图是网格中由五个小正方形组成的图形,根据下列要求画图(涂上阴影)
(1)图①中,添加一块小正方形,使之成为轴对称图形,且有两条对称轴;
(2)图②中,添加一块小正方形,使之成为轴对称图形,且只有一条对称轴(画出一个即可)
2.如图,下列4×4网格图都是由16个相间小正方形组成,每个网格图中有4个小正方形已涂上阴影,在空白小正方形中,选取2个涂上阴影,使6个阴影小正方形组成个轴对称图形,请设计出四种方案.
3.如图,在2×2的正方形网格中,每个小正方形的边长均为1.请分别在下列图中画一个位置不同、顶点都在格点上的三角形,使其与△ABC成轴对称图形.
4.方格纸中每个小方格都的边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.
(1)在图1中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其为轴对称图形;
(2)在图2中画一个格点正方形,使其面积等于10;
(3)直接写出图3中△FGH的面积是
.
5.在七年级我们就学过用一副三角板画出一些特殊度数的角.在八年级第二章,我们学会了一些基本的尺规作图,这些特殊的角也能用尺规作出.下面请各位同学开动脑筋,只用直尺和圆规完成下列作图.
已知:如图,射线OA.
求作:∠AOB,使得∠AOB在射线OA的上方,且∠AOB=45°(保留作图痕迹,不写作法)
6.已知:如图,在△ABC中,AC<AB且∠C=2∠B
(1)用直尺和圆规作出一条过点A的直线1,使得点C关于直线的对称点落在边AB上(不写作法,保留作图痕迹)
(2)设(1)中直线l与边BC的交点为D,请写出线段AB、AC、CD之间的数量关系并说明理由.
7.如图,△ABC中,AB=3,AC=4,BC=5.
(1)试用直尺和圆规,在直线AB上求作点P,使△PBC为等腰三角形.要求:①保留作图痕迹;②若点P有多解,则应作出所有的点P,并在图中依次标注P1、P2、P3、…;
(2)根据(1)求PA的长(所有可能的值)
8.如图,已知△ABC(AC<AB<BC),请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)在边BC上确定一点P,使得PA+PC=BC;
(2)作出一个△DEF,使得:①△DEF是直角三角形;②△DEF的周长等于边BC的长.
9.茅坪民族中学八(2)班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,站在C处的学生小明先拿桔子再拿糖果,然后回到C处,请你在下图帮助他设计一条行走路线,使其所走的总路程最短?
10.如图,为了做好元旦期间的交通安全工作,自贡市交警执勤小队从A处出发,先到公路m上设卡检査,再到公路n上设卡检査,最后再到达B地执行任务,他们应如何走才能使总路程最短?画出图形并说明做法.
11.如图,点P是∠AOB内部一点,现有一只蚂蚁要从P的出发,先到OA,再到OB,最后返回到点P.请作出蚂蚁爬行的最短路径(要求:保留作图痕迹,不写作法.)
12.如图直线l1,l2表示一条河的两岸,且l1∥l2,现要在这条河上建一座桥.桥建在何处才能使从村庄A经过河到村庄B的路线最短?画出示意图,并说明理由.
13.在△ABC中,∠BAC=a,点D,点E在BC上,连接AD,AE.
(1)如图,若a=120°,BA=BE,CA=CD,求∠DAE的度数;
(2)若DA=DB,EA=EC,直接写出∠DAE=
(用a的式子表示).
14.如图,△ABC中,AE=BE,∠AED=∠ABC.
(1)求证:BD平分∠ABC;
(2)若AB=CB,∠AED=4∠EAD,求∠C的度数.
15.已知:在△ABC中,∠B=∠C,D,E分别是线段BC,AC上的一点,且AD=AE,
(1)如图1,若∠BAC=90°,D是BC中点,则∠2的度数为
;
(2)借助图2探究并直接写出∠1和∠2的数量关系
.
16.数学课上,张老师举了下面的例题:
例1等腰三角形ABC中,∠A=110°,求∠B的度数.(答案:35°)
例2等腰三角形ABC中,∠A=40°,求∠B的度数.(答案:40°或70°或100°)
张老师启发同学们进行变式,小敏编了如下两题:
变式1:等腰三角形ABC中,∠A=100°,求∠B的度数.
变式2:等腰三角形ABC中,∠A=45°,求∠B的度数.
(1)请你解答以上两道变式题.
(2)解(1)后,小敏发现,∠A的度数不同,得到∠B的度数的个数也可能不同.如果在等腰三角形ABC中,设∠A=x°,当∠B只有一个度数时,请你探索x的取值范围.
17.在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
(1)如图1,连接BE、CE,则BE=CE吗?说明理由;
(2)若∠BAC=45°,BE的延长线与AC垂直相交于点F时,如图2,BD=AE吗?说明理由.
18.如图,等腰△ABC,点D、E、F分别在BC、AB、AC上,且∠BAC=∠ADE=∠ADF=60°.
(1)在图中找出与∠DAC相等的角,并加以证明;
(2)若AB=6,BE=m,求:AF(用含m的式子表示).
19.如图,在△ABC中,AB=AC,∠BAC=100°,BD平分∠ABC,且BD=AB,连接AD、DC.
(1)求证:∠CAD=∠DBC;
(2)求∠BDC的度数.
20.在△ABC和△DCE中,CA=CB,CD=CE,∠CAB=∠CED=α.
(1)如图1,将AD、EB延长,延长线相交于点O:
①求证:BE=AD;
②用含α的式子表示∠AOB的度数(直接写出结果);
(2)如图2,当α=45°时,连接BD、AE,作CM⊥AE于M点,延长MC与BD交于点N,求证:N是BD的中点.
21.△ABC,直线DE交AB于D,交AC于E,将△ADE沿DE折叠,使A落在同一平面上的A′处,∠A′的两边与BD、CE的夹角分别记为∠1,∠2.
(1)如图①,当A′落在四边形BDEC内部时,探索∠A与∠1+∠2之间的数量关系,并说明理由.
(2)如图②,当A′落在AC右侧时,探索∠A与∠1,∠2之间的数量关系,并说明理由.
22.如图(1),△ABC是一个三角形的纸片,点D、E分别是△ABC边上的两点,
研究(1):如果沿直线DE折叠,则∠BDA′与∠A的关系是
.
研究(2):如果折成图2的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.
研究(3):如果折成图3的形状,猜想∠BDA′、∠CEA′和∠A的关系,并说明理由.
23.图形在折叠过程中会形成相等的边和相等的角,下面是同学们在数学课上所做的三角形、四边形折叠实验,请根据实验过程解决问题:
问题(一)
如图①,一张三角形ABC纸片,点D、E分别是△ABC边上两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′和∠A的数量关系是
;
研究(2):如果折成图②的形状,猜想∠BDA′、∠CEA′和∠A的数量关系是
;
研究(3):如果折成图③的形状,猜想∠BDA′、∠CEA′和∠A的数量关系,并说明理由.
问题(二)
研究(4):将问题(一)推广,如图④,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是
.(直接写出结论)
24.发现(1)如图1,把△ABC沿DE折叠,使点A落在点A’处,请你判断∠1+∠2与∠A有何数量关系,直接写出你的结论,不必说明理由
思考(2)如图2,BI平分∠ABC,CI平分∠ACB,把△ABC折叠,使点A与点I重合,若∠1+∠2=100°,求∠BIC的度数;
拓展(3)如图3,在锐角△ABC中,BF⊥AC于点F,CG⊥AB于点G,BF、CG交于点H,把△ABC折叠使点A和点H重合,试探索∠BHC与∠1+∠2的关系,并证明你的结论.
答案
一、选择题
1.B.2.D.3.C.4.A.5.A.6.B7.C.8.D.
9.D.10.A.11.C.12.D.13.D.14.A.15.B.16.D.
二、解答题
1.解:(1)如图①所示:即为所求;
(2)如图②所示:即为所求.
2.解:如图所示:
3.画对任意三种即可.
.
4.解:(1)如图1所示:
(2)如图2所示:
(3)如图3所示:
△FGH的面积=矩形ABHC的面积﹣△AFG的面积﹣△BGH的面积﹣△FCH的面积
=5×6﹣﹣﹣
=9
故答案为:9.
5.解:如图所示,∠AOB即为所作.
6.解:(1)如图所示,直线AD即为所求;
(2)线段AB、AC、CD之间的数量关系为:AB=AC+CD.
理由:由题可得,AE=AC,∠CAD=∠EAD,AD=AD,
∴△ACD≌△AED(SAS),
∴DE=CD,∠AED=∠C=2∠B,
又∵∠AED=∠B+∠BDE,
∴∠B=∠BDE,
∴BE=DE=CD,
又∵AB=AE+BE,
∴AB=AC+CD.
7.解:(1)如图,点P1、P2、P3、P4为所作;
(2)∵AB=3,AC=4,BC=5.
∴AB2+AC2=BC2,
∴△ABC为直角三角形,∠BAC=90°,
当CP1=CB时,
∵CA⊥BP1,
∴AP1=AB=3;
当BP2=BP3=BC=5时,
AP2=AB+BP2=3+5=8;
AP3=BP3﹣AB=5﹣3=2;
当P4C=P4B时,
设AP4=x,则P4C=P4B=x+3,
在Rt△P4AC中,x2+42=(x+3)2,解得x=,
即AP4=.
综上所述,AP的值可能为2、3、8、.
8.解:(1)如图,作AB的垂直平分线,交BC于点P,则点P即为所求;
(2)如图,①在BC上取点D,过点D作BC的垂线,②在垂线上取点E使DE=DB,连接EC,③作EC的垂直平分线交BC于点F;
∴Rt△DEF即为所求.
9.解:①分别作点C关于OA、OB的对称点是M、N,
②连接MN,分别交OA于D,OB于E.
则C→D→E→C为所求的行走路线.
10.解:如图所示,分别作A、B关于公路m、n的对称点A′、B′,连接A′B′交m、n于M、N两点,连AM、BN,则A→M→N→B即为最短路线.
11.解:如图,
作点P关于OA、OB的对称点P′、P″,
连接P′P″与OA、OB交于点M、N,
则蚂蚁爬行的最短路径为:
PM+MN+PN=P′M+MN+P″N=P′P″.
12.解:如图,先确定AA′与河等宽,且AA′⊥河岸,连接BA′,与河岸的交点就是点C,过点C作CD垂直河岸,交另一河岸于点D,CD就是所求的桥的位置.
理由:由作图过程可知,四边形ACDA′为平行四边形,AD平移至A′C即可得到线段A′B,两点之间,线段最短,由于河宽不变,CD即为桥.
13.解:(1)∵BE=BA,
∴∠BAE=∠BEA,
∴∠B=180°﹣2∠BAE,①
∵CD=CA,
∴∠CAD=∠CDA,
∴∠C=180°﹣2∠CAD,②
①+②得:∠B+∠C=360°﹣2(∠BAE+∠CAD)
∴180°﹣∠BAC=360°﹣2[(∠BAD+∠DAE)+(∠DAE+∠CAE)],
∴﹣∠BAC=180°﹣2[(∠BAD+∠DAE+∠CAE)+∠DAE],
∴﹣∠BAC=180°﹣2(∠BAC+∠DAE),
∴2∠DAE=180°﹣∠BAC.
∵∠BAC=120°,
∴2∠DAE=180°﹣120°=60°,
∴∠DAE=30°,
(2)∵DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
又在△ABC中,∠B+∠C=180°﹣∠BAC=180°﹣α,
∴∠DAB+∠EAC=∠B+∠C=70°,
∴∠DAE=∠BAC﹣(∠DAB+∠EAC)
=α﹣(180°﹣α)=2α﹣180°.
故答案为:2α﹣180°.
14.(1)证明:∵∠AED=∠ABC,∠AED=∠ABE+∠EAB,∠ABC=∠ABE+∠DBC,
∴∠EAB=∠DBC,
∵AE=BE,
∴∠EAB=∠ABE,
∴∠DBC=∠ABE,
∴BD平分∠ABC;
(2)设∠EAD=x,则∠AED=4x,
∵∠AED=∠ABE+∠EAB,∠EAB=∠ABE,BD平分∠ABC,
∴∠BAE=2x,∠ABC=4x,
∴∠BAC=3x,
∵AB=CB,
∴∠BAC=∠C,
∴∠C=3x,
∵∠ABC+∠BAC+∠C﹣180°,
∴4x+3x+3x=180°,
解得,x=18°,
∴∠C=3x=54°,
即∠C的度数是54°.
15.解:(1)∠AED=∠CDE+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,
∴∠AED=∠ADE,
∵∠B=∠C,∠BAC=90°,D是BC中点,
∴∠BAD=45°,
∴∠B+∠BAD=∠EDC+∠C+∠CDE,
即∠BAD=2∠CDE,
∴∠2=22.5°;
(2)∠AED=∠CDE+∠C,∠ADC=∠B+∠BAD,
∵AD=AE,
∴∠AED=∠ADE,
∵AB=AC,
∴∠B=∠C,
∴∠B+∠BAD=∠EDC+∠C+∠CDE,
即∠BAD=2∠CDE,∠1=2∠2.
16.解:(1)变式1:∵∠A=100°,
∴∠A只能为△ABC的顶角,
∵△ABC为等腰三角形,
∴∠B=∠C=×(180°﹣100°)=40°;
变式2:若∠A为顶角,则∠B=(180°﹣∠A)÷2=67.5°;
若∠A为底角,∠B为顶角,则∠B=180°﹣2×45°=90°;
若∠A为底角,∠B为底角,则∠B=45°;
故∠B=67.5°或90°或45°;
(2)分两种情况:
①当90≤x<180时,∠A只能为顶角,
∴∠B的度数只有一个;
②当0<x<90时,当x=60时,等腰三角形ABC是等边三角形,
∴∠B的度数只有一个,
∴当∠B只有一个度数时,请你探索x的取值范围为90≤x<180或60.
17.解:(1)成立.
理由:∵AB=AC,D是BC的中点,
∴∠BAE=∠CAE.
在△ABE和△ACE中,,
∴△ABE≌△ACE(SAS),
∴BE=CE;
(2)成立.
理由:∵∠BAC=45°,BF⊥AF.
∴△ABF为等腰直角三角形
∴AF=BF,
由(1)知AD⊥BC,
∴∠EAF=∠CBF
在△AEF和△BCF中,,
∴△AEF≌△BCF(ASA),
∴AE=BC,
∵BD=BC,
∴BD=AE.
18.解:(1)结论:∠BDE=∠DAC.
理由:∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∴∠C=60°,
∵∠ADB=∠3+∠ADE=∠1+∠C,∠ADE=∠C=60°,
∴∠3=∠1.
(2)如图,在DE上截取DG=DF,连接AG,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠ADE=∠ADF=60°,AD=AD,
∴△ADG≌△ADF(SAS),
∴AG=AF,∠1=∠2,
∵∠3=∠1,
∴∠3=∠2
∵∠AEG=60°+∠3,∠AGE=60°+∠2,
∴∠AEG=∠AGE,
∴AE=AG,
∴AE=AF=6﹣m.
19.证明(1)∵AB=AC,∠BAC=100°
∴∠ABC=∠ACB=40°
∵BD平分∠ABC
∴∠ABD=∠DBC=20°
∵BD=AB
∴∠ADB=∠DAB=80°
∴∠CAD=20°
∴∠CAD=∠DBC
(2)延长AD到点E,使得AE=BC,
∵BD=AB=AC,∠CAD=∠DBC,
∴△DBC≌△CAE,
∴CD=CE,∠BDC=∠ACE,
∴∠CDE=∠CED=α,
∵∠ADB=80°,
∴∠BDE=100°
∴∠BDC=∠ACE=100°+α,
∴20°+100°+α+α=180°,
∴α=30°,
∴∠BDC=130°.
20.解:(1)①∵CA=CB,CD=CE,∠CAB=∠CED=α,
∴∠ACB=180°﹣2α,∠DCE=180°﹣2α,
∴∠ACB=∠DCE,
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB,
∴∠ACD=∠BCE,
在△ACD和△BCE中,,
∴△ACD≌△BCE(SAS),
∴BE=AD;
②∵△ACD≌△BCE,
∴∠CAD=∠CBE=α+∠BAO,
∵∠ABE=∠BOA+∠BAO,
∴∠CBE+α=∠BOA+∠BAO,
∴∠BAO+α+α=∠BOA+∠BAO,
∴∠BOA=2α;
(2)如图2,作BP⊥MN交MN的延长线于P,作DQ⊥MN于Q,
∵∠BCP+∠BCA=∠CAM+∠AMC,
∵∠BCA=∠AMC,
∴∠BCP=∠CAM,
在△CBP与△ACM中,,
∴△CBP≌△ACM(AAS),
∴MC=BP,
同理,CM=DQ,
∴DQ=BP,
在△BPN与△DQN中,,
∴△BPN≌△DQN(AAS),
∴BN=ND,
∴N是BD的中点.
21.解:(1)2∠A=∠1+∠2.理由如下:
如图①.∵∠A+∠A′+∠AEA′+∠ADA′=360°,
又∵∠1+∠ADA′+∠2+∠AEA′=360°,
∴∠A+∠A′=∠1+∠2,
又∵∠A=∠A′,
∴2∠A=∠1+∠2;
(2)2∠A=∠1﹣∠2.理由如下:
如图②,设DA′交AC于点F.
∵∠1=∠A+∠DFA,∠DFA=∠A′+∠2,
∴∠1=∠A+∠A′+∠2,
∴∠A+∠A′=∠1﹣∠2,
∵△A′DE是由△ADE沿直线DE折叠而得,
∴∠A=∠A′,
∴2∠A=∠1﹣∠2.
22.解:(1)∠BDA′=2∠A;
故答案为:∠BDA′=2∠A;
(2)∠BDA′+∠CEA′=2∠A,
理由:在四边形ADA′E中,∠A+∠DA′E+∠ADA′+∠A′EA=360°
∴∠A+∠DA′E=360°﹣∠ADA′﹣∠A′EA
∵∠BDA′+∠ADA′=180°,∠CEA′+∠A′EA=180°
∴∠BDA′+∠CEA′=360°﹣∠ADA′﹣∠A′EA
∴∠BDA′+∠CEA′=∠A+∠DA′E
∵△A′DE是由△ADE沿直线DE折叠而得
∴∠A=∠DA′E
∴∠BDA′+∠CEA′=2∠A;
(3)∠BDA′﹣∠CEA′=2∠A
理由:DA′交AC于点F,
∵∠BDA′=∠A+∠DFA,∠DFA=∠A′+∠CEA′
∴∠BDA′=∠A+∠A′+∠CEA′
∴∠BDA′﹣∠CEA′=∠A+∠A′
∵△A′DE是由△ADE沿直线DE折叠而得
∴∠A=∠DA′E
∴∠BDA′﹣∠CEA′=2∠A.
23.解:(1)∵根据折叠的性质可知∠DA′E=∠A,∠DA′E+∠A=∠BDA′,
′∴∠BDA=2∠A.
故答案为:∠BDA=2∠A;
(2)由图形折叠的性质可知,∠CEA′=180°﹣2∠DEA′…①,∠BDA′=180°﹣2∠A′DE…②,
①+②得,∠BDA′+∠CEA′=360°﹣2(∠DEA′+∠A′DE
即∠BDA′+∠CEA′=360°﹣2(180°﹣∠A),
故∠BDA′+∠CEA′=2∠A.
故答案为:∠BDA′+∠CEA′=2∠A;
(3)∠BDA′﹣∠CEA′=2∠A.
证明如下:
连接AA′构造等腰三角形,
∠BDA′=2∠DA'A,∠CEA'=2∠EA'A,
得∠BDA'﹣∠CEA'=2∠A,
(4)如图④,由图形折叠的性质可知∠1=180°﹣2∠AEF,∠2=180°﹣2∠BFE,
两式相加得,∠1+∠2=360°﹣2(∠AEF+∠BFE)
即∠1+∠2=360°﹣2(360°﹣∠A﹣∠B),
所以,∠1+∠2=2(∠A+∠B)﹣360°.
故答案为:∠1+∠2=2(∠A+∠B)﹣360°.
24.解:(1)∠1+∠2=2∠A;
理由:根据翻折的性质,∠ADE=(180°﹣∠1),∠AED=(180°﹣∠2),
∵∠A+∠ADE+∠AED=180°,
∴∠A+(180﹣∠1)+(180﹣∠2)=180°,
整理得2∠A=∠1+∠2;
(2)由(1)∠1+∠2=2∠A,得2∠A=100°,
∴∠A=50°
∵IB平分∠ABC,IC平分∠ACB,
∴∠IBC+∠ICB=(∠ABC+∠ACB)=(180°﹣∠A)=90°﹣∠A,
∴∠BIC=180°﹣(∠IBC+∠ICB)=180°﹣(90°﹣∠A)=90°+×50°=115°;
(3)∵BF⊥AC,CG⊥AB,
∴∠AFH+∠AGH=90°+90°=180°,
∠FHG+∠A=180°,
∴∠BHC=∠FHG=180°﹣∠A,
由(1)知∠1+∠2=2∠A,
∴∠A=(∠1+∠2),
∴∠BHC=180°﹣(∠1+∠2).
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
