10.3 直角三角形课件(共30张PPT)
文档属性
| 名称 | 10.3 直角三角形课件(共30张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-03 00:00:00 | ||
图片预览










文档简介
第十章 三角形的有关证明
3 直角三角形
知识点一 勾股定理
内容
应用格式
注意问题
勾股定理
知识点一 勾股定理
内容
应用格式
注意问题
勾股定理
直角三角形两条直角边的平方和等于斜边的平方
如图所示,在Rt△ABC中,∵∠C=90°,∴a2+b2=c2
“直角三角形”是应用勾股定理的前提条件,如果已知条件中没有直角三角形,要想利用勾股定理,必须先构造直角三角形.应用勾股定理时,要注意确定哪条边是直角三角形的最长边,也就是斜边,在Rt△ABC中,斜边不一定是c,当∠A=90°时,a2=b2+c2,当∠B=90°时,b2=a2+c2.注意公式的变形由a2+b2=c2,可得a2=c2-b2,b2=c2-a2
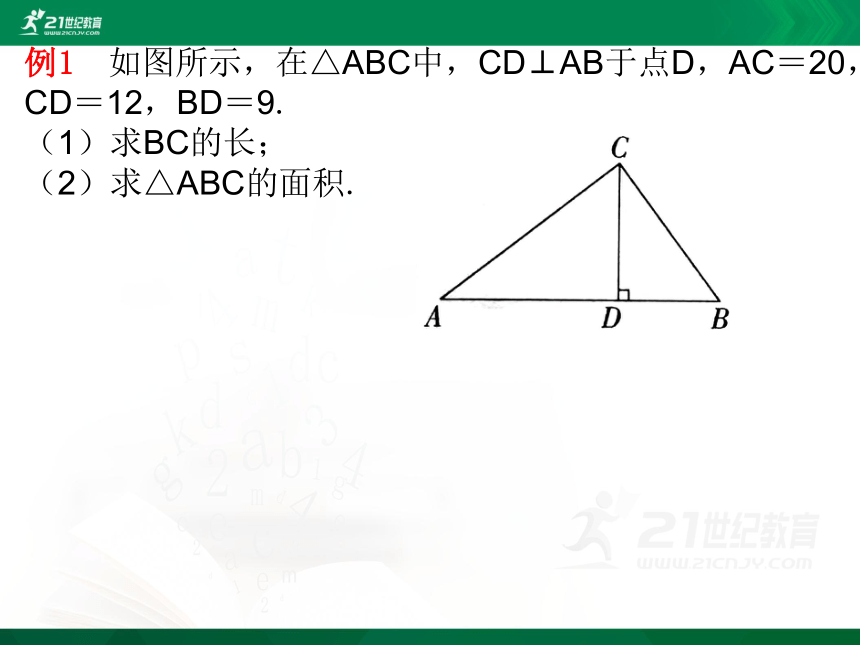
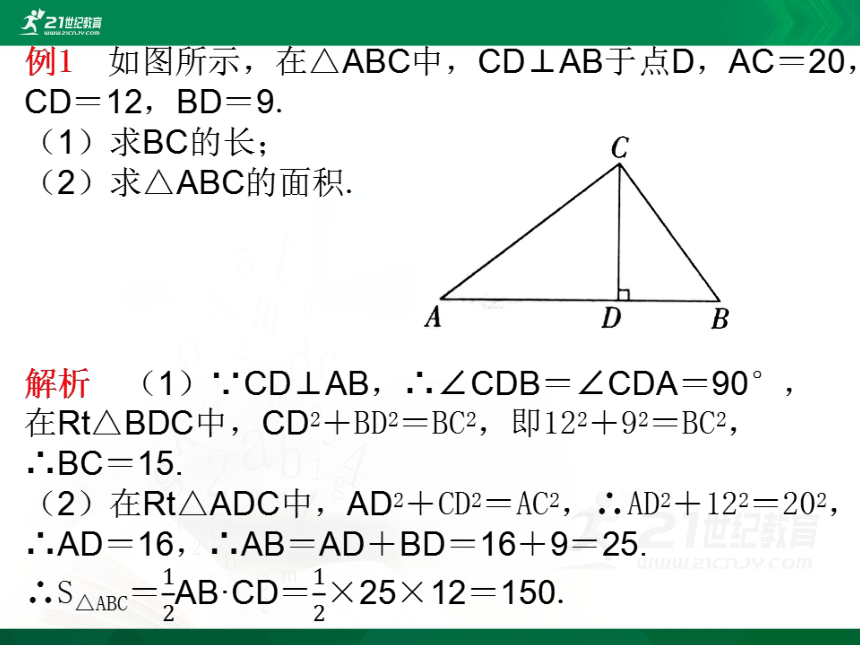
例1 如图所示,在△ABC中,CD⊥AB于点D,AC=20,CD=12,BD=9.
(1)求BC的长;
(2)求△ABC的面积.
知识点二 勾股定理的逆定理
内容
应用格式
注意问题
勾股定理的逆定理
温馨提示
知识点二 勾股定理的逆定理
内容
应用格式
注意问题
勾股定理的逆定理
如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
如图所示,在△ABC中,∵a2+b2=c2,∴∠C=90°
应用勾股定理的逆定理判断三角形是不是直角三角形时,首先找出最长边,然后计算较短两边的平方和并与最长边的平方进行比较,看它们是否相等,若相等,则三角形是直角三角形,否则,就不是直角三角形
温馨提示
到目前为止,判定直角三角形的方法有:①说明三角形中有一个角为直角;②说明三角形中有两边互相垂直;③勾股定理的逆定理
知识点三 互逆命题与互逆定理
内容
特别说明
互逆命题
互逆定理
温馨提示
知识点三 互逆命题与互逆定理
内容
特别说明
互逆命题
在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题
任何命题都有逆命题,真命题的逆命题不一定是真命题,假命题的逆命题不一定是假命题
互逆定理
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,其中一个定理称为另一个定理的逆定理
一个定理,不一定有定理逆定理
温馨提示
写原命题的逆命题时,最好先将原命题改写成“如果…那么…”的形式,“如果”引出的部分是条件,“那么”引出的部分是结论,再根据改写后的命题写出原命题的逆命题
例3 命题“直角三角形两锐角互余”的逆命题是________________________________.
例3 命题“直角三角形两锐角互余”的逆命题是________________________________.
解析 因为“直角三角形两锐角互余”的条件是“一个三角形是直角三角形”,结论是“两个锐角互余”,所以逆命题是“有两个锐角互余的三角形是直角三角形”.
例3 命题“直角三角形两锐角互余”的逆命题是________________________________.
解析 因为“直角三角形两锐角互余”的条件是“一个三角形是直角三角形”,结论是“两个锐角互余”,所以逆命题是“有两个锐角互余的三角形是直角三角形”.
答案 有两个锐角互余的三角形是直角三角形
知识点四 “斜边、直角边”(或“HL”)
内容
应用格式
图形表示
“斜边、直角边”(或“HL”)
知识详解
知识点四 “斜边、直角边”(或“HL”)
内容
应用格式
图形表示
“斜边、直角边”(或“HL”)
斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”)
在Rt△ABC和Rt△A′B'C′中(∠C与∠C′为直角)
∵
∴Rt△ABC≌Rt△A'B'C'(HL)
知识详解
(1)“HL”是判定两个直角三角形全等特有的定理,应用此定理时要注意:①要保证两个三角形是直角三角形;②斜边相等;③任意一条直角边对应相等.
(2)一般三角形全等的判定方法对判定两个直角三角形全等全部适用,也就是说判定两个直角三角形全等共有5种方法,即“SSS”“SAS”“ASA”“AAS”“HL”
例4 如图所示,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:△ABE≌△CBF.
例4 如图所示,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:△ABE≌△CBF.
证明 ∠ABC=90°,∴∠CBF=90°.
在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL).
经典例题
题型一 勾股定理的应用
例1 如图所示,一竖直的木杆在离地面6尺高的B处折断,木杆顶端C落在离木杆底端A的8尺处木杆折断之前有多高?
题型一 勾股定理的应用
例1 如图所示,一竖直的木杆在离地面6尺高的B处折断,木杆顶端C落在离木杆底端A的8尺处木杆折断之前有多高?
解析 ∵易知△ABC是直角三角形,∴BC= ,
∵AB=6尺,AC=8尺,∴BC= =10(尺),
∴木杆折断之前的高度=AB+BC=6+10=16(尺).
题型一 勾股定理的应用
例1 如图所示,一竖直的木杆在离地面6尺高的B处折断,木杆顶端C落在离木杆底端A的8尺处木杆折断之前有多高?
解析 ∵易知△ABC是直角三角形,∴BC= ,
∵AB=6尺,AC=8尺,∴BC= =10(尺),
∴木杆折断之前的高度=AB+BC=6+10=16(尺).
点拨 利用勾股定理解决实际问题时,首先根据题意构造直角三角形,再运用勾股定理计算边长有时需设适当的未知数列方程解决.
题型二 勾股定理的逆定理的应用
例2 如图所示,从帐篷支撑杆AB的顶部A向地面拉一根绳子AC固定帐篷,若绳子的长度为5.5米,固定点C到帐篷支撑杆底部B的距离是4.5米,现有一根高为3.2米的竹竿,它能否做帐篷的支撑杆?请说明理由.
题型二 勾股定理的逆定理的应用
解析 不能.理由如下:
∵在△ABC中,AC=5.5米,BC=4.5米,
∴AC2=30.25,BC2=20.25.
∵3.22=10.24,30.25≠20.25+10.24,
∴一根高为3.2米的竹竿不能做帐篷的支撑杆.
题型二 勾股定理的逆定理的应用
解析 不能.理由如下:
∵在△ABC中,AC=5.5米,BC=4.5米,
∴AC2=30.25,BC2=20.25.
∵3.22=10.24,30.25≠20.25+10.24,
∴一根高为3.2米的竹竿不能做帐篷的支撑杆.
点拨
知道三角形的三边,判断三角形是不是直角三角形,用勾股定理的逆定理判断即可.
易错易混
易错点 在直角三角形中,不确定第三边是直角边还是斜边时,没有分类讨论而致错
在直角三角形中,已知两边的长可求第三边,但是当没有说明已知的两边是直角三角形的直角边还是斜边时,要注意分类讨论.
例 三角形两边的长分别为3和5,要使这个三角形是直角三角形,则第三边的长是__________.
3 直角三角形
知识点一 勾股定理
内容
应用格式
注意问题
勾股定理
知识点一 勾股定理
内容
应用格式
注意问题
勾股定理
直角三角形两条直角边的平方和等于斜边的平方
如图所示,在Rt△ABC中,∵∠C=90°,∴a2+b2=c2
“直角三角形”是应用勾股定理的前提条件,如果已知条件中没有直角三角形,要想利用勾股定理,必须先构造直角三角形.应用勾股定理时,要注意确定哪条边是直角三角形的最长边,也就是斜边,在Rt△ABC中,斜边不一定是c,当∠A=90°时,a2=b2+c2,当∠B=90°时,b2=a2+c2.注意公式的变形由a2+b2=c2,可得a2=c2-b2,b2=c2-a2
例1 如图所示,在△ABC中,CD⊥AB于点D,AC=20,CD=12,BD=9.
(1)求BC的长;
(2)求△ABC的面积.
知识点二 勾股定理的逆定理
内容
应用格式
注意问题
勾股定理的逆定理
温馨提示
知识点二 勾股定理的逆定理
内容
应用格式
注意问题
勾股定理的逆定理
如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
如图所示,在△ABC中,∵a2+b2=c2,∴∠C=90°
应用勾股定理的逆定理判断三角形是不是直角三角形时,首先找出最长边,然后计算较短两边的平方和并与最长边的平方进行比较,看它们是否相等,若相等,则三角形是直角三角形,否则,就不是直角三角形
温馨提示
到目前为止,判定直角三角形的方法有:①说明三角形中有一个角为直角;②说明三角形中有两边互相垂直;③勾股定理的逆定理
知识点三 互逆命题与互逆定理
内容
特别说明
互逆命题
互逆定理
温馨提示
知识点三 互逆命题与互逆定理
内容
特别说明
互逆命题
在两个命题中,如果一个命题的条件和结论分别是另一个命题的结论和条件,那么这两个命题称为互逆命题,其中一个命题称为另一个命题的逆命题
任何命题都有逆命题,真命题的逆命题不一定是真命题,假命题的逆命题不一定是假命题
互逆定理
如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,其中一个定理称为另一个定理的逆定理
一个定理,不一定有定理逆定理
温馨提示
写原命题的逆命题时,最好先将原命题改写成“如果…那么…”的形式,“如果”引出的部分是条件,“那么”引出的部分是结论,再根据改写后的命题写出原命题的逆命题
例3 命题“直角三角形两锐角互余”的逆命题是________________________________.
例3 命题“直角三角形两锐角互余”的逆命题是________________________________.
解析 因为“直角三角形两锐角互余”的条件是“一个三角形是直角三角形”,结论是“两个锐角互余”,所以逆命题是“有两个锐角互余的三角形是直角三角形”.
例3 命题“直角三角形两锐角互余”的逆命题是________________________________.
解析 因为“直角三角形两锐角互余”的条件是“一个三角形是直角三角形”,结论是“两个锐角互余”,所以逆命题是“有两个锐角互余的三角形是直角三角形”.
答案 有两个锐角互余的三角形是直角三角形
知识点四 “斜边、直角边”(或“HL”)
内容
应用格式
图形表示
“斜边、直角边”(或“HL”)
知识详解
知识点四 “斜边、直角边”(或“HL”)
内容
应用格式
图形表示
“斜边、直角边”(或“HL”)
斜边和一条直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”)
在Rt△ABC和Rt△A′B'C′中(∠C与∠C′为直角)
∵
∴Rt△ABC≌Rt△A'B'C'(HL)
知识详解
(1)“HL”是判定两个直角三角形全等特有的定理,应用此定理时要注意:①要保证两个三角形是直角三角形;②斜边相等;③任意一条直角边对应相等.
(2)一般三角形全等的判定方法对判定两个直角三角形全等全部适用,也就是说判定两个直角三角形全等共有5种方法,即“SSS”“SAS”“ASA”“AAS”“HL”
例4 如图所示,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:△ABE≌△CBF.
例4 如图所示,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.求证:△ABE≌△CBF.
证明 ∠ABC=90°,∴∠CBF=90°.
在Rt△ABE和Rt△CBF中,
∴Rt△ABE≌Rt△CBF(HL).
经典例题
题型一 勾股定理的应用
例1 如图所示,一竖直的木杆在离地面6尺高的B处折断,木杆顶端C落在离木杆底端A的8尺处木杆折断之前有多高?
题型一 勾股定理的应用
例1 如图所示,一竖直的木杆在离地面6尺高的B处折断,木杆顶端C落在离木杆底端A的8尺处木杆折断之前有多高?
解析 ∵易知△ABC是直角三角形,∴BC= ,
∵AB=6尺,AC=8尺,∴BC= =10(尺),
∴木杆折断之前的高度=AB+BC=6+10=16(尺).
题型一 勾股定理的应用
例1 如图所示,一竖直的木杆在离地面6尺高的B处折断,木杆顶端C落在离木杆底端A的8尺处木杆折断之前有多高?
解析 ∵易知△ABC是直角三角形,∴BC= ,
∵AB=6尺,AC=8尺,∴BC= =10(尺),
∴木杆折断之前的高度=AB+BC=6+10=16(尺).
点拨 利用勾股定理解决实际问题时,首先根据题意构造直角三角形,再运用勾股定理计算边长有时需设适当的未知数列方程解决.
题型二 勾股定理的逆定理的应用
例2 如图所示,从帐篷支撑杆AB的顶部A向地面拉一根绳子AC固定帐篷,若绳子的长度为5.5米,固定点C到帐篷支撑杆底部B的距离是4.5米,现有一根高为3.2米的竹竿,它能否做帐篷的支撑杆?请说明理由.
题型二 勾股定理的逆定理的应用
解析 不能.理由如下:
∵在△ABC中,AC=5.5米,BC=4.5米,
∴AC2=30.25,BC2=20.25.
∵3.22=10.24,30.25≠20.25+10.24,
∴一根高为3.2米的竹竿不能做帐篷的支撑杆.
题型二 勾股定理的逆定理的应用
解析 不能.理由如下:
∵在△ABC中,AC=5.5米,BC=4.5米,
∴AC2=30.25,BC2=20.25.
∵3.22=10.24,30.25≠20.25+10.24,
∴一根高为3.2米的竹竿不能做帐篷的支撑杆.
点拨
知道三角形的三边,判断三角形是不是直角三角形,用勾股定理的逆定理判断即可.
易错易混
易错点 在直角三角形中,不确定第三边是直角边还是斜边时,没有分类讨论而致错
在直角三角形中,已知两边的长可求第三边,但是当没有说明已知的两边是直角三角形的直角边还是斜边时,要注意分类讨论.
例 三角形两边的长分别为3和5,要使这个三角形是直角三角形,则第三边的长是__________.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
