2020-2021学年北师大版八年级数学下册第二章 2.5~2.6 同步测试题(Word版含答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册第二章 2.5~2.6 同步测试题(Word版含答案) | 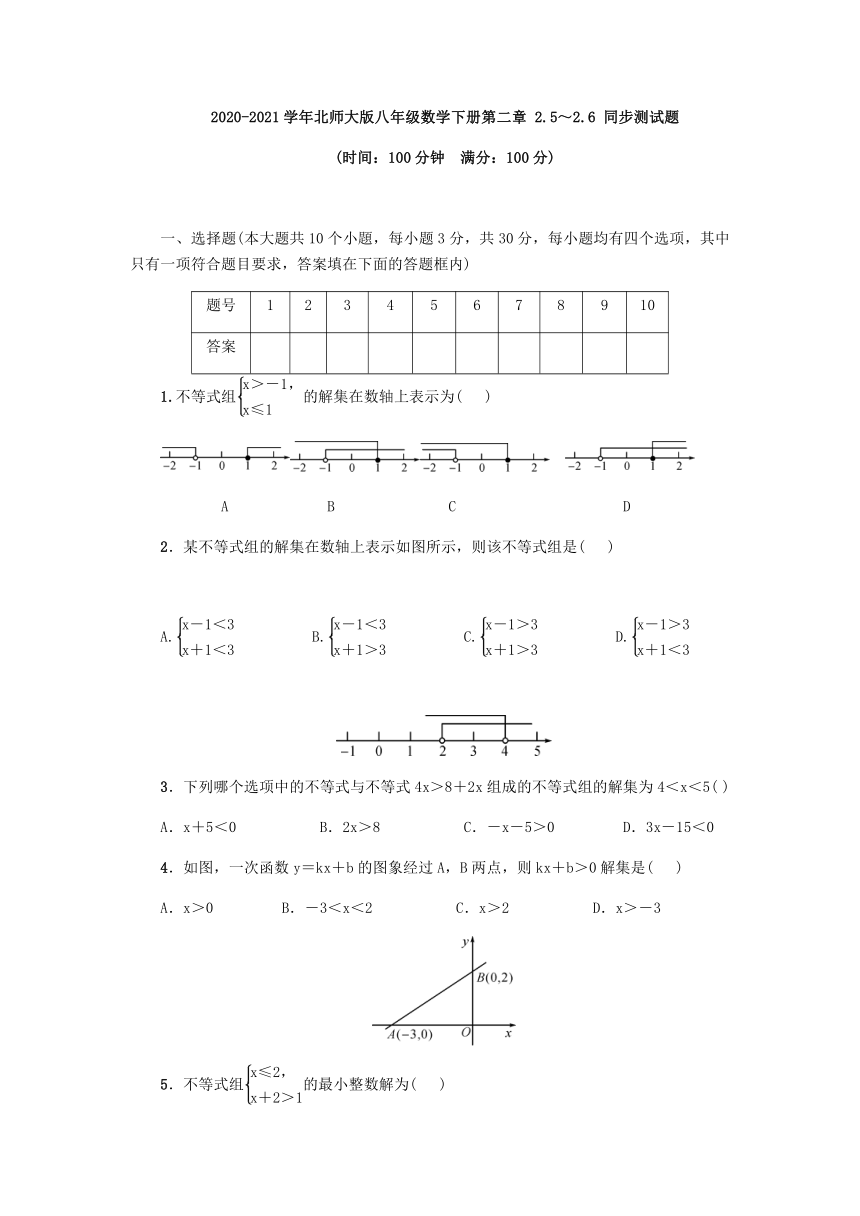 | |
| 格式 | zip | ||
| 文件大小 | 51.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 18:25:47 | ||
图片预览





文档简介
2020-2021学年北师大版八年级数学下册第二章
2.5~2.6
同步测试题
(时间:100分钟 满分:100分)
一、选择题(本大题共10个小題,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案填在下面的答题框内)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.不等式组的解集在数轴上表示为(
)
A
B
C
D
2.某不等式组的解集在数轴上表示如图所示,则该不等式组是(
)
A.
B.
C.
D.
3.下列哪个选项中的不等式与不等式4x>8+2x组成的不等式组的解集为4<x<5(
)
A.x+5<0
B.2x>8
C.-x-5>0
D.3x-15<0
4.如图,一次函数y=kx+b的图象经过A,B两点,则kx+b>0解集是(
)
A.x>0
B.-3<x<2
C.x>2
D.x>-3
5.不等式组的最小整数解为(
)
A.-1
B.0
C.1
D.2
6.已知点P(1-a,2a+6)在第四象限,则a的取值范围是(
)
A.a<-3
B.-3<a<1
C.a>-3
D.a>1
7.若关于x的不等式组无解,则a的取值范围是(
)
A.a≤-3
B.a<-3
C.a>3
D.a≥3
8.若关于x的不等式组的解集为x<3,则k的取值范围为(
)
A.k>1
B.k<1
C.k≥1
D.k≤1
9.如果三个数a-1,3-a,2a在数轴上所对应的点从左到右依次排列,那么a的取值范围是(
)
A.1B.-1C.-1D.以上都不对
10.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型
办卡费用/元
每次游泳收费/元
A类
50
25
B类
200
20
C类
400
15
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元.若一年内在该游泳馆游泳的次数介于40~50次之间,则最省钱的方式为(C)
购买A类会员年卡
B.购买B类会员年卡
C.购买C类会员年卡
D.不购买会员年卡
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.不等式组的解集是_____________.
12.若x同时满足不等式2x+3>0和x-2≤x+,则x的取值范围是_________.
13.一次函数y=ax+3与y=bx-1的图象如图所示,其交点为B(-3,m),则不等式ax-bx+3<-1的解集为_________.
14.若关于x的不等式组的解集为1<x<3,则a的值为4.
三、解答题(本大题共6个小题,共54分,解答题应写出必要的文字说明、证明过程或演算步骤)
15.(6分)解不等式组:
16.(8分)解不等式组:把它的解集表示在数轴上,并求出不等式组的非负整数解.
17.(8分)我们定义=ad-bc,例如=2×5-3×4=10-12=-2.求不等式组1<<3的解集.
18.(10分)已知关于x的不等式组只有唯一的整数解,求a的取值范围.
19.(10分)某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示.
(1)分别写出用租书卡和会员卡租书的金额y(元)与租书时间x(天)之间的函数关系式;
(2)通过计算说明小明一年租书时间x在什么范围时,采用会员卡的租书方式更合算?
20.(12分)某超市销售每台进价分别为200元、170元的A,B两种型号的电风扇,下表是近两周销售情况:
销售时段
销售量
A种型号
B种型号
销售收入
第一周
3台
5台
1
800元
第二周
4台
10台
3
100元
(1)求A,B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5
400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1
400元的目标?若能,请给出采购方案;若不能,请说明理由.
.
参考答案
2020-2021学年北师大版八年级数学下册第二章
2.5~2.6
同步测试题(含答案)
(时间:100分钟 满分:100分)
一、选择题(本大题共10个小題,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案填在下面的答题框内)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
B
D
D
B
A
A
C
A
C
1.不等式组的解集在数轴上表示为(B)
A
B
C
D
2.某不等式组的解集在数轴上表示如图所示,则该不等式组是(B)
A.
B.
C.
D.
3.下列哪个选项中的不等式与不等式4x>8+2x组成的不等式组的解集为4<x<5(D)
A.x+5<0
B.2x>8
C.-x-5>0
D.3x-15<0
4.如图,一次函数y=kx+b的图象经过A,B两点,则kx+b>0解集是(D)
A.x>0
B.-3<x<2
C.x>2
D.x>-3
5.不等式组的最小整数解为(B)
A.-1
B.0
C.1
D.2
6.已知点P(1-a,2a+6)在第四象限,则a的取值范围是(A)
A.a<-3
B.-3<a<1
C.a>-3
D.a>1
7.若关于x的不等式组无解,则a的取值范围是(A)
A.a≤-3
B.a<-3
C.a>3
D.a≥3
8.若关于x的不等式组的解集为x<3,则k的取值范围为(C)
A.k>1
B.k<1
C.k≥1
D.k≤1
9.如果三个数a-1,3-a,2a在数轴上所对应的点从左到右依次排列,那么a的取值范围是(A)
A.1B.-1C.-1D.以上都不对
10.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型
办卡费用/元
每次游泳收费/元
A类
50
25
B类
200
20
C类
400
15
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元.若一年内在该游泳馆游泳的次数介于40~50次之间,则最省钱的方式为(C)
A.购买A类会员年卡
B.购买B类会员年卡
C.购买C类会员年卡
D.不购买会员年卡
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.不等式组的解集是-1<x≤2.
12.若x同时满足不等式2x+3>0和x-2≤x+,则x的取值范围是-<x≤.
13.一次函数y=ax+3与y=bx-1的图象如图所示,其交点为B(-3,m),则不等式ax-bx+3<-1的解集为x<-3.
14.若关于x的不等式组的解集为1<x<3,则a的值为4.
三、解答题(本大题共6个小题,共54分,解答题应写出必要的文字说明、证明过程或演算步骤)
15.(6分)解不等式组:
解:解不等式①,得x≤3.
解不等式②,得x≥0.
∴不等式组的解集为0≤x≤3.
16.(8分)解不等式组:把它的解集表示在数轴上,并求出不等式组的非负整数解.
解:解不等式①,得x≥-.
解不等式②,得x<3.
∴不等式组的解集是-≤x<3.
不等式组的解集在数轴上表示:
∴不等式组的非负整数解是0,1,2.
17.(8分)我们定义=ad-bc,例如=2×5-3×4=10-12=-2.求不等式组1<<3的解集.
解:根据题意,得
解不等式①,得x<1.
解不等式②,得x>.
∴不等式组的解集为<x<1.
18.(10分)已知关于x的不等式组只有唯一的整数解,求a的取值范围.
解:解不等式x-a>0,得x>a.
解不等式5-2x>1,得x<2.
∵不等式组有唯一整数解,
∴不等式组的解集为a<x<2.
∴0≤a<1.
19.(10分)某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示.
(1)分别写出用租书卡和会员卡租书的金额y(元)与租书时间x(天)之间的函数关系式;
(2)通过计算说明小明一年租书时间x在什么范围时,采用会员卡的租书方式更合算?
解:(1)设使用会员卡的租书金额y1(元)与租书时间x(天)之间的函数关系式为y1=kx+b,根据题意,得
解得∴y1=0.3x+20.
设使用租书卡的租书金额y2(元)与租书时间x(天)之间的函数关系式为y2=k1x,根据题意,得
50=100k1,解得k1=0.5.∴y2=0.5x.
故使用会员卡租书的金额与租书时间之间的函数关系式为y1=0.3x+20,使用租书卡租书的金额与租书时间的函数关系式为y2=0.5x.
(2)令0.3x+20<0.5x,解得x>100.
∴小明一年租书时间x>100时,采用会员卡的方式租书更合算.
20.(12分)某超市销售每台进价分别为200元、170元的A,B两种型号的电风扇,下表是近两周销售情况:
销售时段
销售量
A种型号
B种型号
销售收入
第一周
3台
5台
1
800元
第二周
4台
10台
3
100元
(1)求A,B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5
400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1
400元的目标?若能,请给出采购方案;若不能,请说明理由.
解:
(1)设A,B两种型号电风扇的销售单价分别为x元、y元,依题意,得
解得
答:A,B两种型号的电风扇的销售单价分别为250元、210元.
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(30-a)台,依题意,得
200a+170(30-a)≤5
400.
解得a≤10.
答:A种型号电风扇最多能采购10台.
(3)依题意,得(250-200)a+(210-170)(30-a)=1
400.
解得a=20.
∵a≤10,
∴在(2)的条件下,超市销售完这30台电风扇不能实现目标.
2.5~2.6
同步测试题
(时间:100分钟 满分:100分)
一、选择题(本大题共10个小題,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案填在下面的答题框内)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.不等式组的解集在数轴上表示为(
)
A
B
C
D
2.某不等式组的解集在数轴上表示如图所示,则该不等式组是(
)
A.
B.
C.
D.
3.下列哪个选项中的不等式与不等式4x>8+2x组成的不等式组的解集为4<x<5(
)
A.x+5<0
B.2x>8
C.-x-5>0
D.3x-15<0
4.如图,一次函数y=kx+b的图象经过A,B两点,则kx+b>0解集是(
)
A.x>0
B.-3<x<2
C.x>2
D.x>-3
5.不等式组的最小整数解为(
)
A.-1
B.0
C.1
D.2
6.已知点P(1-a,2a+6)在第四象限,则a的取值范围是(
)
A.a<-3
B.-3<a<1
C.a>-3
D.a>1
7.若关于x的不等式组无解,则a的取值范围是(
)
A.a≤-3
B.a<-3
C.a>3
D.a≥3
8.若关于x的不等式组的解集为x<3,则k的取值范围为(
)
A.k>1
B.k<1
C.k≥1
D.k≤1
9.如果三个数a-1,3-a,2a在数轴上所对应的点从左到右依次排列,那么a的取值范围是(
)
A.1
10.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型
办卡费用/元
每次游泳收费/元
A类
50
25
B类
200
20
C类
400
15
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元.若一年内在该游泳馆游泳的次数介于40~50次之间,则最省钱的方式为(C)
购买A类会员年卡
B.购买B类会员年卡
C.购买C类会员年卡
D.不购买会员年卡
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.不等式组的解集是_____________.
12.若x同时满足不等式2x+3>0和x-2≤x+,则x的取值范围是_________.
13.一次函数y=ax+3与y=bx-1的图象如图所示,其交点为B(-3,m),则不等式ax-bx+3<-1的解集为_________.
14.若关于x的不等式组的解集为1<x<3,则a的值为4.
三、解答题(本大题共6个小题,共54分,解答题应写出必要的文字说明、证明过程或演算步骤)
15.(6分)解不等式组:
16.(8分)解不等式组:把它的解集表示在数轴上,并求出不等式组的非负整数解.
17.(8分)我们定义=ad-bc,例如=2×5-3×4=10-12=-2.求不等式组1<<3的解集.
18.(10分)已知关于x的不等式组只有唯一的整数解,求a的取值范围.
19.(10分)某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示.
(1)分别写出用租书卡和会员卡租书的金额y(元)与租书时间x(天)之间的函数关系式;
(2)通过计算说明小明一年租书时间x在什么范围时,采用会员卡的租书方式更合算?
20.(12分)某超市销售每台进价分别为200元、170元的A,B两种型号的电风扇,下表是近两周销售情况:
销售时段
销售量
A种型号
B种型号
销售收入
第一周
3台
5台
1
800元
第二周
4台
10台
3
100元
(1)求A,B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5
400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1
400元的目标?若能,请给出采购方案;若不能,请说明理由.
.
参考答案
2020-2021学年北师大版八年级数学下册第二章
2.5~2.6
同步测试题(含答案)
(时间:100分钟 满分:100分)
一、选择题(本大题共10个小題,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案填在下面的答题框内)
题号
1
2
3
4
5
6
7
8
9
10
答案
B
B
D
D
B
A
A
C
A
C
1.不等式组的解集在数轴上表示为(B)
A
B
C
D
2.某不等式组的解集在数轴上表示如图所示,则该不等式组是(B)
A.
B.
C.
D.
3.下列哪个选项中的不等式与不等式4x>8+2x组成的不等式组的解集为4<x<5(D)
A.x+5<0
B.2x>8
C.-x-5>0
D.3x-15<0
4.如图,一次函数y=kx+b的图象经过A,B两点,则kx+b>0解集是(D)
A.x>0
B.-3<x<2
C.x>2
D.x>-3
5.不等式组的最小整数解为(B)
A.-1
B.0
C.1
D.2
6.已知点P(1-a,2a+6)在第四象限,则a的取值范围是(A)
A.a<-3
B.-3<a<1
C.a>-3
D.a>1
7.若关于x的不等式组无解,则a的取值范围是(A)
A.a≤-3
B.a<-3
C.a>3
D.a≥3
8.若关于x的不等式组的解集为x<3,则k的取值范围为(C)
A.k>1
B.k<1
C.k≥1
D.k≤1
9.如果三个数a-1,3-a,2a在数轴上所对应的点从左到右依次排列,那么a的取值范围是(A)
A.1
10.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:
会员年卡类型
办卡费用/元
每次游泳收费/元
A类
50
25
B类
200
20
C类
400
15
例如,购买A类会员年卡,一年内游泳20次,消费50+25×20=550元.若一年内在该游泳馆游泳的次数介于40~50次之间,则最省钱的方式为(C)
A.购买A类会员年卡
B.购买B类会员年卡
C.购买C类会员年卡
D.不购买会员年卡
二、填空题(本大题共4个小题,每小题4分,共16分,答案写在题中的横线上)
11.不等式组的解集是-1<x≤2.
12.若x同时满足不等式2x+3>0和x-2≤x+,则x的取值范围是-<x≤.
13.一次函数y=ax+3与y=bx-1的图象如图所示,其交点为B(-3,m),则不等式ax-bx+3<-1的解集为x<-3.
14.若关于x的不等式组的解集为1<x<3,则a的值为4.
三、解答题(本大题共6个小题,共54分,解答题应写出必要的文字说明、证明过程或演算步骤)
15.(6分)解不等式组:
解:解不等式①,得x≤3.
解不等式②,得x≥0.
∴不等式组的解集为0≤x≤3.
16.(8分)解不等式组:把它的解集表示在数轴上,并求出不等式组的非负整数解.
解:解不等式①,得x≥-.
解不等式②,得x<3.
∴不等式组的解集是-≤x<3.
不等式组的解集在数轴上表示:
∴不等式组的非负整数解是0,1,2.
17.(8分)我们定义=ad-bc,例如=2×5-3×4=10-12=-2.求不等式组1<<3的解集.
解:根据题意,得
解不等式①,得x<1.
解不等式②,得x>.
∴不等式组的解集为<x<1.
18.(10分)已知关于x的不等式组只有唯一的整数解,求a的取值范围.
解:解不等式x-a>0,得x>a.
解不等式5-2x>1,得x<2.
∵不等式组有唯一整数解,
∴不等式组的解集为a<x<2.
∴0≤a<1.
19.(10分)某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示.
(1)分别写出用租书卡和会员卡租书的金额y(元)与租书时间x(天)之间的函数关系式;
(2)通过计算说明小明一年租书时间x在什么范围时,采用会员卡的租书方式更合算?
解:(1)设使用会员卡的租书金额y1(元)与租书时间x(天)之间的函数关系式为y1=kx+b,根据题意,得
解得∴y1=0.3x+20.
设使用租书卡的租书金额y2(元)与租书时间x(天)之间的函数关系式为y2=k1x,根据题意,得
50=100k1,解得k1=0.5.∴y2=0.5x.
故使用会员卡租书的金额与租书时间之间的函数关系式为y1=0.3x+20,使用租书卡租书的金额与租书时间的函数关系式为y2=0.5x.
(2)令0.3x+20<0.5x,解得x>100.
∴小明一年租书时间x>100时,采用会员卡的方式租书更合算.
20.(12分)某超市销售每台进价分别为200元、170元的A,B两种型号的电风扇,下表是近两周销售情况:
销售时段
销售量
A种型号
B种型号
销售收入
第一周
3台
5台
1
800元
第二周
4台
10台
3
100元
(1)求A,B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5
400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1
400元的目标?若能,请给出采购方案;若不能,请说明理由.
解:
(1)设A,B两种型号电风扇的销售单价分别为x元、y元,依题意,得
解得
答:A,B两种型号的电风扇的销售单价分别为250元、210元.
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(30-a)台,依题意,得
200a+170(30-a)≤5
400.
解得a≤10.
答:A种型号电风扇最多能采购10台.
(3)依题意,得(250-200)a+(210-170)(30-a)=1
400.
解得a=20.
∵a≤10,
∴在(2)的条件下,超市销售完这30台电风扇不能实现目标.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
