2020-2021学年北师大版七年级数学下册第二章2.1-2.3 同步练习题(含答案)
文档属性
| 名称 | 2020-2021学年北师大版七年级数学下册第二章2.1-2.3 同步练习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 105.1KB | ||
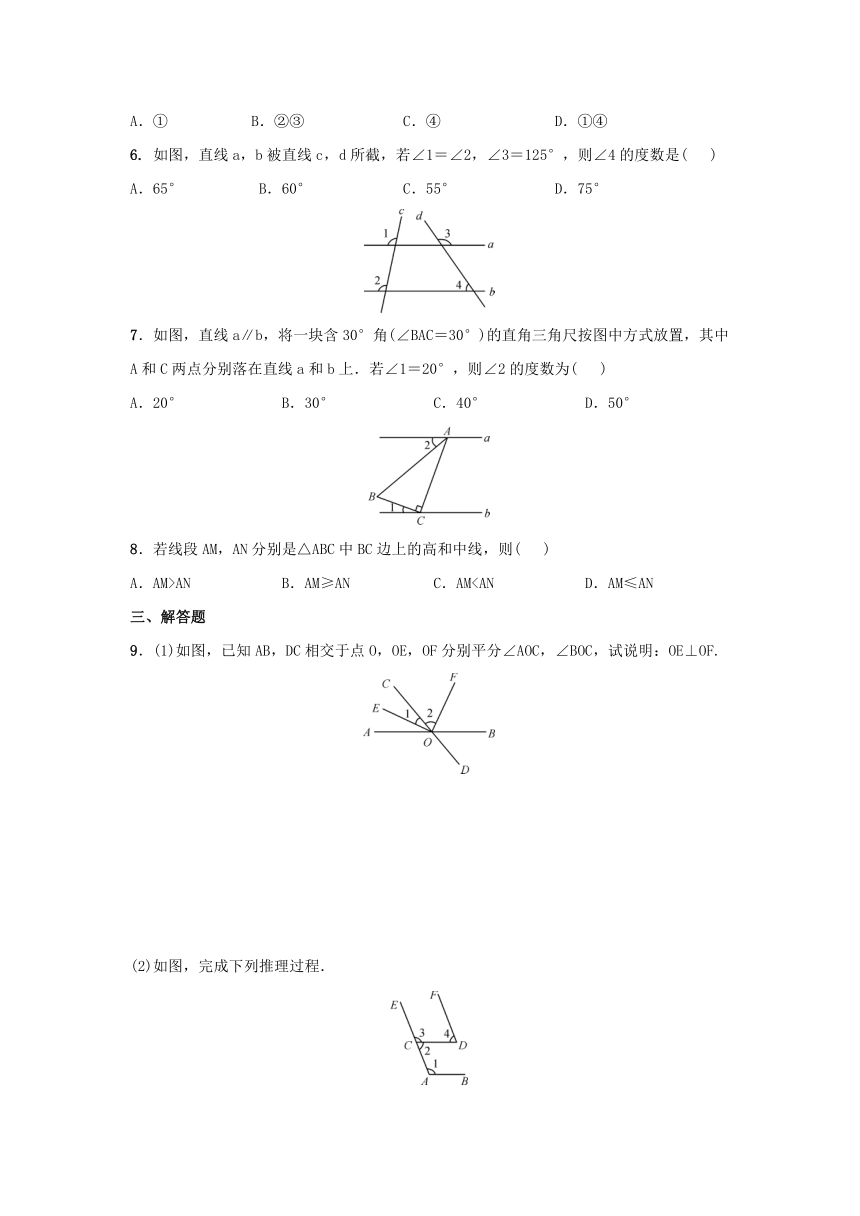
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 18:28:08 | ||
图片预览

文档简介
2020-2021学年北师大版七年级数学下册第二章2.1-2.3
同步练习题
A组(基础题)
一、填空题
1.如图,将一副三角板的直角顶点重合在一起,其中∠AOB和∠COD是直角.若∠1=55°,则∠2=_______.
2.
(1)下列说法中错误的有_______个.
①有且只有一条直线垂直于已知直线;
②从直线外一点到这条直线的垂线段,叫作这点到这条直线的距离;
③互相垂直的两条线段一定相交;
④直线
c外一点A与直线c上各点连接而成的所有线段中,最短线段的长是3
cm,则点A到直线c的距离是3
cm.
(2))将一副三角板(含30°,45°,60°,90°角)按如图所示的位置摆放在直尺上,则∠1的度数为_______度.
3.
如图,从点O(点O在直线PQ上)照射到抛物线上的光线OB,反射以后沿着与直线PQ平行的方向射出.若∠POB=60°,则∠ABO=_______.
4.如图,AB∥CD,DE∥CB,∠B=35°,则∠D=_______.
二、选择题
5.
下列说法:①两直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行;④两直线平行,同位角相等.其中是平行线的性质的是(
)
A.①
B.②③
C.④
D.①④
6.
如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数是(
)
A.65°
B.60°
C.55°
D.75°
7.如图,直线a∥b,将一块含30°角(∠BAC=30°)的直角三角尺按图中方式放置,其中A和C两点分别落在直线a和b上.若∠1=20°,则∠2的度数为(
)
A.20°
B.30°
C.40°
D.50°
8.若线段AM,AN分别是△ABC中BC边上的高和中线,则(
)
A.AM>AN
B.AM≥AN
C.AMD.AM≤AN
三、解答题
9.(1)如图,已知AB,DC相交于点O,OE,OF分别平分∠AOC,∠BOC,试说明:OE⊥OF.
(2)如图,完成下列推理过程.
①已知∠1=108°,∠2=72°,由∠1+∠2=108°+72°=180°,可得_______∥____,根据是_______;
②已知∠1=108°,∠3=108°,由∠1=108°=∠3,可得____∥____,根据是____
③已知∠2=72°,∠4=72°,由∠2=72°=∠4,可得____∥____,根据是____
10.(1)如图,在直角三角形ABC中,∠ACB=90°,将Rt△ABC向下翻折,使点A与点C重合,折痕为DE,试说明:DE∥BC.
(2)如图,已知∠1=∠2,∠A=∠C,试说明:AE∥BC.
B组(中档题)
一、填空题
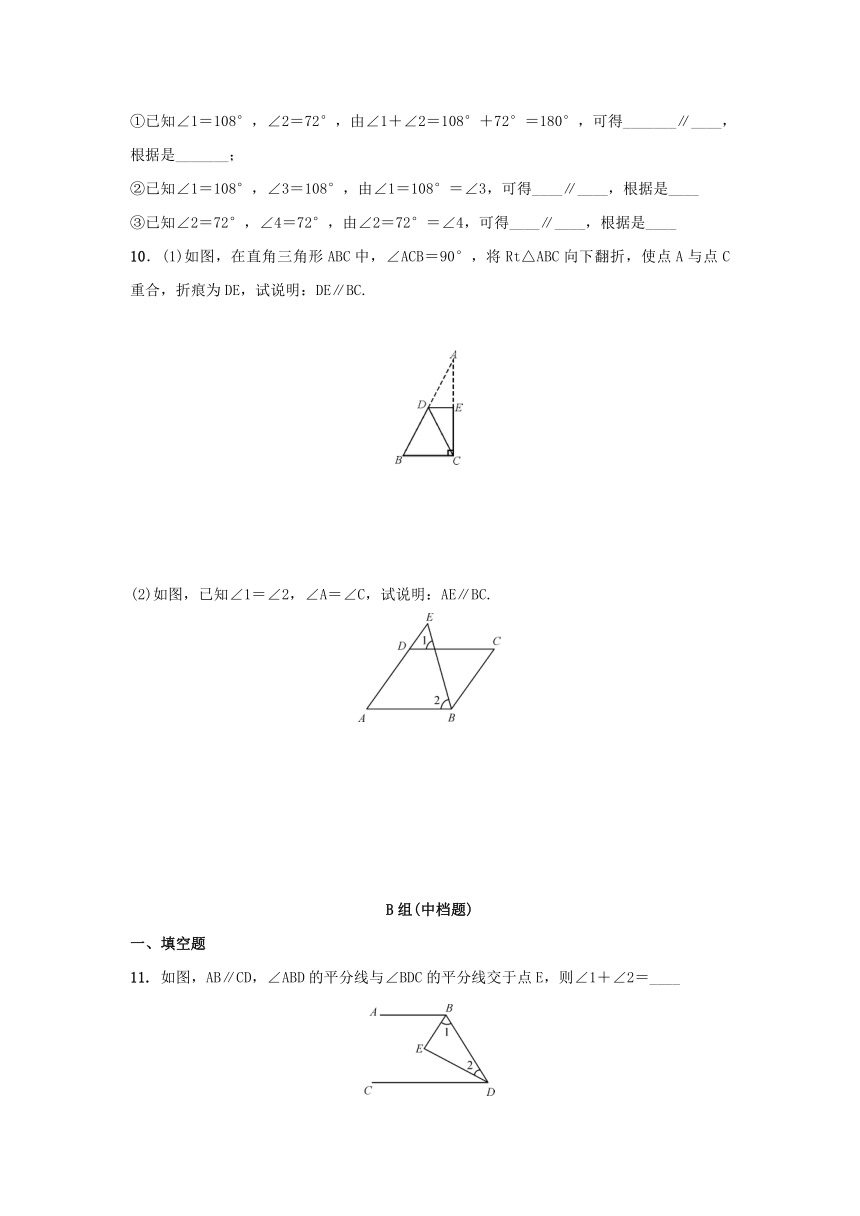
11.
如图,AB∥CD,∠ABD的平分线与∠BDC的平分线交于点E,则∠1+∠2=____
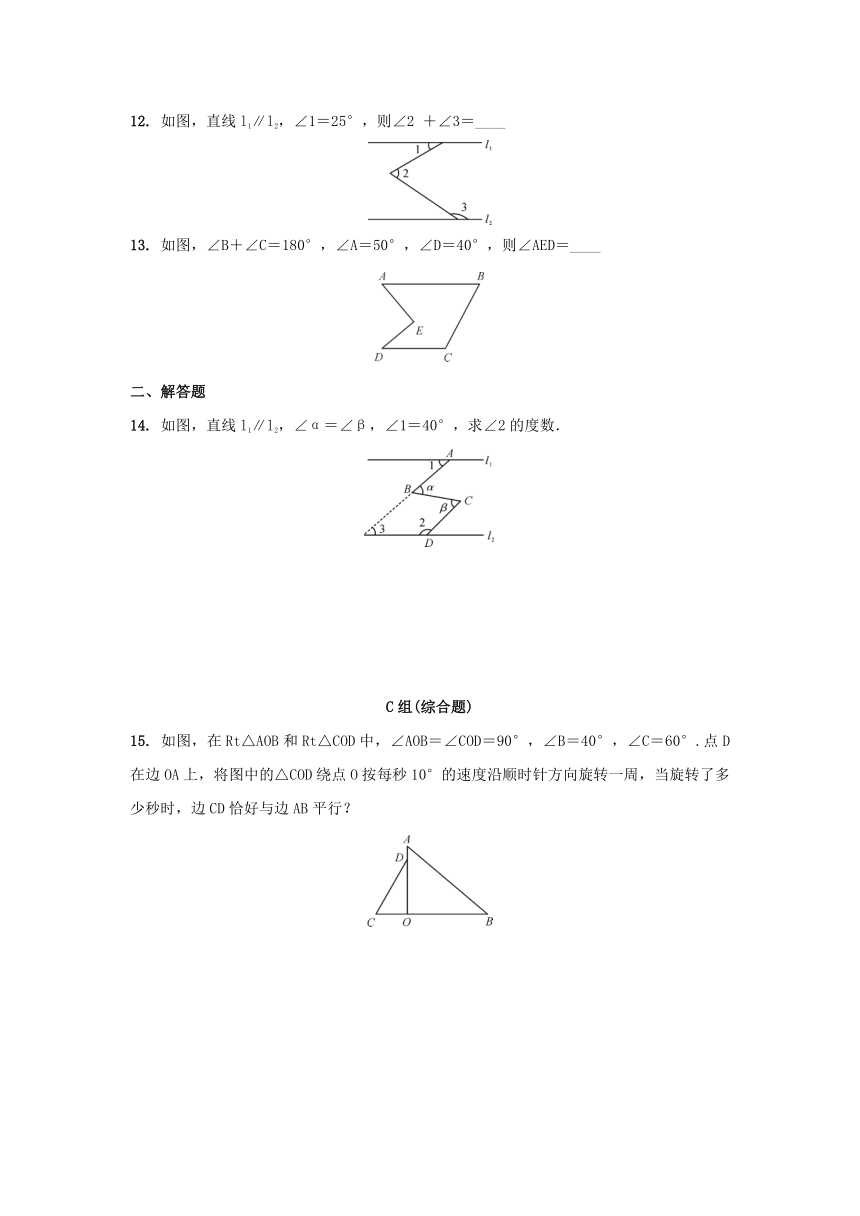
12.
如图,直线l1∥l2,∠1=25°,则∠2
+∠3=____
13.
如图,∠B+∠C=180°,∠A=50°,∠D=40°,则∠AED=____
二、解答题
14.
如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数.
C组(综合题)
15.
如图,在Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°.点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,当旋转了多少秒时,边CD恰好与边AB平行?
参考答案
2020-2021学年北师大版七年级数学下册第二章2.1-2.3
同步练习题
A组(基础题)
一、填空题
1.如图,将一副三角板的直角顶点重合在一起,其中∠AOB和∠COD是直角.若∠1=55°,则∠2=55°.
2.
(1)下列说法中错误的有3个.
①有且只有一条直线垂直于已知直线;
②从直线外一点到这条直线的垂线段,叫作这点到这条直线的距离;
③互相垂直的两条线段一定相交;
④直线
c外一点A与直线c上各点连接而成的所有线段中,最短线段的长是3
cm,则点A到直线c的距离是3
cm.
(2))将一副三角板(含30°,45°,60°,90°角)按如图所示的位置摆放在直尺上,则∠1的度数为75度.
3.
如图,从点O(点O在直线PQ上)照射到抛物线上的光线OB,反射以后沿着与直线PQ平行的方向射出.若∠POB=60°,则∠ABO=60°.
4.如图,AB∥CD,DE∥CB,∠B=35°,则∠D=145°.
二、选择题
5.
下列说法:①两直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行;④两直线平行,同位角相等.其中是平行线的性质的是(D)
A.①
B.②③
C.④
D.①④
6.
如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数是(C)
A.65°
B.60°
C.55°
D.75°
7.如图,直线a∥b,将一块含30°角(∠BAC=30°)的直角三角尺按图中方式放置,其中A和C两点分别落在直线a和b上.若∠1=20°,则∠2的度数为(C)
A.20°
B.30°
C.40°
D.50°
8.若线段AM,AN分别是△ABC中BC边上的高和中线,则(D)
A.AM>AN
B.AM≥AN
C.AMD.AM≤AN
三、解答题
9.(1)如图,已知AB,DC相交于点O,OE,OF分别平分∠AOC,∠BOC,试说明:OE⊥OF.
解:∵OE,OF分别平分∠AOC与∠BOC,
∴∠1=∠AOC,∠2=∠BOC.
∴∠1
+∠2=∠AOC+∠BOC=(∠AOC+∠BOC).
又∵∠AOC+∠BOC=180°,
∴∠1+∠2=×180°=90°,
∴OE⊥OF.
(2)如图,完成下列推理过程.
①已知∠1=108°,∠2=72°,由∠1+∠2=108°+72°=180°,可得AB∥CD,根据是同旁内角互补,两直线平行;
②已知∠1=108°,∠3=108°,由∠1=108°=∠3,可得AB∥CD,根据是同位角相等,两直线平行;
③已知∠2=72°,∠4=72°,由∠2=72°=∠4,可得AE∥DF,根据是内错角相等,两直线平行.
10.(1)如图,在直角三角形ABC中,∠ACB=90°,将Rt△ABC向下翻折,使点A与点C重合,折痕为DE,试说明:DE∥BC.
解:∵将Rt△ABC向下翻折,使点A与点C重合,折痕为DE,
∴∠AED=∠CED=90°.
又∵∠ACB=90°,
∴∠AED=∠ACB=90°.
∴DE∥BC.
(2)如图,已知∠1=∠2,∠A=∠C,试说明:AE∥BC.
解:∵∠1=∠2,
∴
DC∥AB.
∴∠ADC+∠A=180°.
又∵∠A=∠C,
∴∠ADC+∠C=180°.
∴AE∥BC.
B组(中档题)
一、填空题
11.
如图,AB∥CD,∠ABD的平分线与∠BDC的平分线交于点E,则∠1+∠2=90°.
12.
如图,直线l1∥l2,∠1=25°,则∠2
+∠3=205°.
13.
如图,∠B+∠C=180°,∠A=50°,∠D=40°,则∠AED=90°.
二、解答题
14.
如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数.
解:如图.
∵l1∥l2,
∴∠3=∠1=40°.
∵∠α=∠β,
∴AB∥CD.
∴∠2+∠3=180°.
∴∠2=180°-∠3=180°-40°=140°.
C组(综合题)
15.
如图,在Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°.点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,当旋转了多少秒时,边CD恰好与边AB平行?
解:分两种情况:
当两三角形在点O的同侧时,如图1,设CD与OB相交于点E.
∵AB∥CD,
∴∠CEO=∠B=40°.
∵∠C=60°,
∴∠OOE=180°-60°-40°-80°.
∴∠DOE=∠COD-∠COE=10°.
∴旋转角∠AOD=∠AOB+∠DOE=90°+10°=100°.
∵每秒旋转10°,
∴旋转的时间为100÷10=10(秒).
当两三角形在点O的异侧时,如图2,延长BO与CD相交于点E.
∵AB∥CD,
∴∠CEO=∠B=40°.
∵∠C=60°,
∴∠COE=180°-60°-40°=80°.
∴旋转角为360°-∠COE=360°-80°=280°.
∵每秒旋转10°,
∴旋转的时间为280÷10=28(秒).
综上所述,当旋转了10秒或28秒时,边CD恰好与边AB平行.
同步练习题
A组(基础题)
一、填空题
1.如图,将一副三角板的直角顶点重合在一起,其中∠AOB和∠COD是直角.若∠1=55°,则∠2=_______.
2.
(1)下列说法中错误的有_______个.
①有且只有一条直线垂直于已知直线;
②从直线外一点到这条直线的垂线段,叫作这点到这条直线的距离;
③互相垂直的两条线段一定相交;
④直线
c外一点A与直线c上各点连接而成的所有线段中,最短线段的长是3
cm,则点A到直线c的距离是3
cm.
(2))将一副三角板(含30°,45°,60°,90°角)按如图所示的位置摆放在直尺上,则∠1的度数为_______度.
3.
如图,从点O(点O在直线PQ上)照射到抛物线上的光线OB,反射以后沿着与直线PQ平行的方向射出.若∠POB=60°,则∠ABO=_______.
4.如图,AB∥CD,DE∥CB,∠B=35°,则∠D=_______.
二、选择题
5.
下列说法:①两直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行;④两直线平行,同位角相等.其中是平行线的性质的是(
)
A.①
B.②③
C.④
D.①④
6.
如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数是(
)
A.65°
B.60°
C.55°
D.75°
7.如图,直线a∥b,将一块含30°角(∠BAC=30°)的直角三角尺按图中方式放置,其中A和C两点分别落在直线a和b上.若∠1=20°,则∠2的度数为(
)
A.20°
B.30°
C.40°
D.50°
8.若线段AM,AN分别是△ABC中BC边上的高和中线,则(
)
A.AM>AN
B.AM≥AN
C.AM
三、解答题
9.(1)如图,已知AB,DC相交于点O,OE,OF分别平分∠AOC,∠BOC,试说明:OE⊥OF.
(2)如图,完成下列推理过程.
①已知∠1=108°,∠2=72°,由∠1+∠2=108°+72°=180°,可得_______∥____,根据是_______;
②已知∠1=108°,∠3=108°,由∠1=108°=∠3,可得____∥____,根据是____
③已知∠2=72°,∠4=72°,由∠2=72°=∠4,可得____∥____,根据是____
10.(1)如图,在直角三角形ABC中,∠ACB=90°,将Rt△ABC向下翻折,使点A与点C重合,折痕为DE,试说明:DE∥BC.
(2)如图,已知∠1=∠2,∠A=∠C,试说明:AE∥BC.
B组(中档题)
一、填空题
11.
如图,AB∥CD,∠ABD的平分线与∠BDC的平分线交于点E,则∠1+∠2=____
12.
如图,直线l1∥l2,∠1=25°,则∠2
+∠3=____
13.
如图,∠B+∠C=180°,∠A=50°,∠D=40°,则∠AED=____
二、解答题
14.
如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数.
C组(综合题)
15.
如图,在Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°.点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,当旋转了多少秒时,边CD恰好与边AB平行?
参考答案
2020-2021学年北师大版七年级数学下册第二章2.1-2.3
同步练习题
A组(基础题)
一、填空题
1.如图,将一副三角板的直角顶点重合在一起,其中∠AOB和∠COD是直角.若∠1=55°,则∠2=55°.
2.
(1)下列说法中错误的有3个.
①有且只有一条直线垂直于已知直线;
②从直线外一点到这条直线的垂线段,叫作这点到这条直线的距离;
③互相垂直的两条线段一定相交;
④直线
c外一点A与直线c上各点连接而成的所有线段中,最短线段的长是3
cm,则点A到直线c的距离是3
cm.
(2))将一副三角板(含30°,45°,60°,90°角)按如图所示的位置摆放在直尺上,则∠1的度数为75度.
3.
如图,从点O(点O在直线PQ上)照射到抛物线上的光线OB,反射以后沿着与直线PQ平行的方向射出.若∠POB=60°,则∠ABO=60°.
4.如图,AB∥CD,DE∥CB,∠B=35°,则∠D=145°.
二、选择题
5.
下列说法:①两直线平行,同旁内角互补;②同位角相等,两直线平行;③内错角相等,两直线平行;④两直线平行,同位角相等.其中是平行线的性质的是(D)
A.①
B.②③
C.④
D.①④
6.
如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4的度数是(C)
A.65°
B.60°
C.55°
D.75°
7.如图,直线a∥b,将一块含30°角(∠BAC=30°)的直角三角尺按图中方式放置,其中A和C两点分别落在直线a和b上.若∠1=20°,则∠2的度数为(C)
A.20°
B.30°
C.40°
D.50°
8.若线段AM,AN分别是△ABC中BC边上的高和中线,则(D)
A.AM>AN
B.AM≥AN
C.AM
三、解答题
9.(1)如图,已知AB,DC相交于点O,OE,OF分别平分∠AOC,∠BOC,试说明:OE⊥OF.
解:∵OE,OF分别平分∠AOC与∠BOC,
∴∠1=∠AOC,∠2=∠BOC.
∴∠1
+∠2=∠AOC+∠BOC=(∠AOC+∠BOC).
又∵∠AOC+∠BOC=180°,
∴∠1+∠2=×180°=90°,
∴OE⊥OF.
(2)如图,完成下列推理过程.
①已知∠1=108°,∠2=72°,由∠1+∠2=108°+72°=180°,可得AB∥CD,根据是同旁内角互补,两直线平行;
②已知∠1=108°,∠3=108°,由∠1=108°=∠3,可得AB∥CD,根据是同位角相等,两直线平行;
③已知∠2=72°,∠4=72°,由∠2=72°=∠4,可得AE∥DF,根据是内错角相等,两直线平行.
10.(1)如图,在直角三角形ABC中,∠ACB=90°,将Rt△ABC向下翻折,使点A与点C重合,折痕为DE,试说明:DE∥BC.
解:∵将Rt△ABC向下翻折,使点A与点C重合,折痕为DE,
∴∠AED=∠CED=90°.
又∵∠ACB=90°,
∴∠AED=∠ACB=90°.
∴DE∥BC.
(2)如图,已知∠1=∠2,∠A=∠C,试说明:AE∥BC.
解:∵∠1=∠2,
∴
DC∥AB.
∴∠ADC+∠A=180°.
又∵∠A=∠C,
∴∠ADC+∠C=180°.
∴AE∥BC.
B组(中档题)
一、填空题
11.
如图,AB∥CD,∠ABD的平分线与∠BDC的平分线交于点E,则∠1+∠2=90°.
12.
如图,直线l1∥l2,∠1=25°,则∠2
+∠3=205°.
13.
如图,∠B+∠C=180°,∠A=50°,∠D=40°,则∠AED=90°.
二、解答题
14.
如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数.
解:如图.
∵l1∥l2,
∴∠3=∠1=40°.
∵∠α=∠β,
∴AB∥CD.
∴∠2+∠3=180°.
∴∠2=180°-∠3=180°-40°=140°.
C组(综合题)
15.
如图,在Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°.点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,当旋转了多少秒时,边CD恰好与边AB平行?
解:分两种情况:
当两三角形在点O的同侧时,如图1,设CD与OB相交于点E.
∵AB∥CD,
∴∠CEO=∠B=40°.
∵∠C=60°,
∴∠OOE=180°-60°-40°-80°.
∴∠DOE=∠COD-∠COE=10°.
∴旋转角∠AOD=∠AOB+∠DOE=90°+10°=100°.
∵每秒旋转10°,
∴旋转的时间为100÷10=10(秒).
当两三角形在点O的异侧时,如图2,延长BO与CD相交于点E.
∵AB∥CD,
∴∠CEO=∠B=40°.
∵∠C=60°,
∴∠COE=180°-60°-40°=80°.
∴旋转角为360°-∠COE=360°-80°=280°.
∵每秒旋转10°,
∴旋转的时间为280÷10=28(秒).
综上所述,当旋转了10秒或28秒时,边CD恰好与边AB平行.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
