2020-2021学年 苏科版七年级数学下册-9.5 多项式的因式分解(1)课件(共16张ppt)
文档属性
| 名称 | 2020-2021学年 苏科版七年级数学下册-9.5 多项式的因式分解(1)课件(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
9.5
多项式的因式分解(1)
一、温故知新
37×2.8+37×5+37×2.2
37×2.8+37×5+37×2.2
解:原式=
37×(2.8+5+2.2)
计算:
=37×10
=370
m(a+b+c)=
ma+mb+mc
ma+mb+mc=m(a+b+c)
反过来
像这样,把一个多项式写成几个整式的积的形式,叫做多项式的因式分解。
整式乘法
因式分解
(x+1)(x
?
1)=
x2
?
1
x2
?
1
=
(x+1)(x
?
1)
(a+b)(c+d)=
ac+ad+bc+bd
ac+ad+bc+bd
=
(a+b)(c+d)
(1)(a
+1)(a?1)
=
a2?1;
(2)a2?1
=
(a
+1)(a?1)
;
(3)8a2b3c
=
2a2·2b3·2c
;
(4)
x2+2x+6=x(x+2)+6;
(5)
下列各式由左边到右边的变形,哪些是因式分解,哪些不是?
辨析:
不是
是
不是
不是
不是
ma+mb+mc
ma+mb+mc
二、探索活动
公因式
把多项式写成公因式与另一个多项式的积的形式,这种分解因式的方法叫做
提公因式法
。
m
=
(a+b+c)
找出下列多项式各项的公因式.
(1)a2b+ab2
(2)3x2
?
6x3;
(3)
9abc?6a2b2+12abc2
;
ab
3ab
3x2
二、探索活动
苏科数学
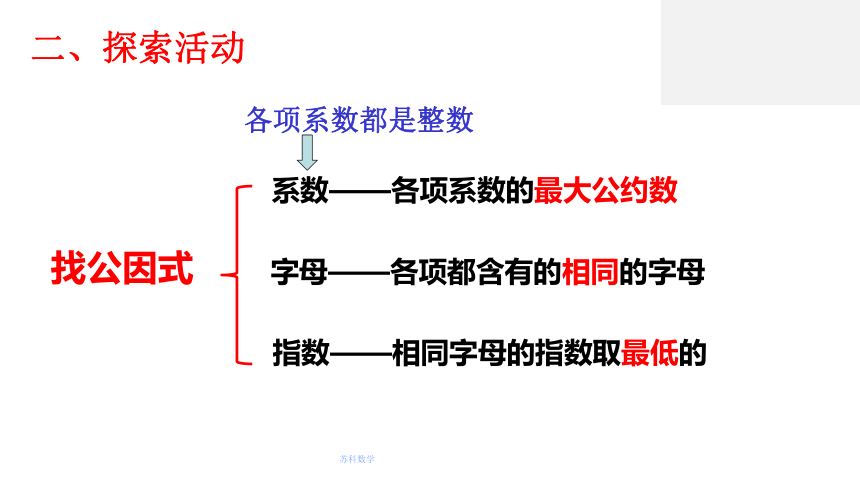
系数——各项系数的最大公约数
字母——各项都含有的相同的字母
指数——相同字母的指数取最低的
各项系数都是整数
二、探索活动
找公因式
三、例题讲解
例1
把下列各式分解因式:
(2)
12ab2c
?
6ab
;
(3)
?
2m3+8m2
?
12m
.
(1)
5x3?10x2
;
(1)
6m2n-9mn2+15mn
;
(2)
3x3-6x2y+3x
;
(3)
?
x2y+4xy
?
5y
.
把下列各式分解因式:
巩固练习1:
例2
把下列各式分解因式:
(2)
3a(x?y)?2b(y?x)
;
(3)
6a(x?y)2
?2(y?x)2
.
(1)
3a(x+y)?2b(x+y)
;
1.已知a+b=-4,ab=2,求a2b+ab2的值.
2.试说明
82018
-
82017
一定能被7整除.
四、拓展提升
找公因式
因式分解
提公因式法
课堂小结
方法1
关键
方法
系数
字母
指数
方法2
方法…
把下列各式分解因式
(1)
(x
?
y)3x+(y
?
x)3y
;
(2)
(a
?
b)2
(2a+b)
+
(b
?
a)2
(a+2b)
.
思考:
必做题:教科书P87:习题9.5
1、2
课后作业
选做题:
如果n是自然数,那么n2+n是奇数还是偶数?
谢
谢!
9.5
多项式的因式分解(1)
一、温故知新
37×2.8+37×5+37×2.2
37×2.8+37×5+37×2.2
解:原式=
37×(2.8+5+2.2)
计算:
=37×10
=370
m(a+b+c)=
ma+mb+mc
ma+mb+mc=m(a+b+c)
反过来
像这样,把一个多项式写成几个整式的积的形式,叫做多项式的因式分解。
整式乘法
因式分解
(x+1)(x
?
1)=
x2
?
1
x2
?
1
=
(x+1)(x
?
1)
(a+b)(c+d)=
ac+ad+bc+bd
ac+ad+bc+bd
=
(a+b)(c+d)
(1)(a
+1)(a?1)
=
a2?1;
(2)a2?1
=
(a
+1)(a?1)
;
(3)8a2b3c
=
2a2·2b3·2c
;
(4)
x2+2x+6=x(x+2)+6;
(5)
下列各式由左边到右边的变形,哪些是因式分解,哪些不是?
辨析:
不是
是
不是
不是
不是
ma+mb+mc
ma+mb+mc
二、探索活动
公因式
把多项式写成公因式与另一个多项式的积的形式,这种分解因式的方法叫做
提公因式法
。
m
=
(a+b+c)
找出下列多项式各项的公因式.
(1)a2b+ab2
(2)3x2
?
6x3;
(3)
9abc?6a2b2+12abc2
;
ab
3ab
3x2
二、探索活动
苏科数学
系数——各项系数的最大公约数
字母——各项都含有的相同的字母
指数——相同字母的指数取最低的
各项系数都是整数
二、探索活动
找公因式
三、例题讲解
例1
把下列各式分解因式:
(2)
12ab2c
?
6ab
;
(3)
?
2m3+8m2
?
12m
.
(1)
5x3?10x2
;
(1)
6m2n-9mn2+15mn
;
(2)
3x3-6x2y+3x
;
(3)
?
x2y+4xy
?
5y
.
把下列各式分解因式:
巩固练习1:
例2
把下列各式分解因式:
(2)
3a(x?y)?2b(y?x)
;
(3)
6a(x?y)2
?2(y?x)2
.
(1)
3a(x+y)?2b(x+y)
;
1.已知a+b=-4,ab=2,求a2b+ab2的值.
2.试说明
82018
-
82017
一定能被7整除.
四、拓展提升
找公因式
因式分解
提公因式法
课堂小结
方法1
关键
方法
系数
字母
指数
方法2
方法…
把下列各式分解因式
(1)
(x
?
y)3x+(y
?
x)3y
;
(2)
(a
?
b)2
(2a+b)
+
(b
?
a)2
(a+2b)
.
思考:
必做题:教科书P87:习题9.5
1、2
课后作业
选做题:
如果n是自然数,那么n2+n是奇数还是偶数?
谢
谢!
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
