2020-2021学年八年级数学人教版下册《第18章平行四边形》章末综合优生辅导训练(附答案)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册《第18章平行四边形》章末综合优生辅导训练(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 293.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 00:00:00 | ||
图片预览



文档简介
2021年度人教版八年级数学下册《第18章平行四边形》章末综合优生辅导训练(附答案)
1.若平行四边形的两条对角线长为6
cm和16
cm,则下列长度的线段可作为平行四边形边长的是( )
A.5cm
B.8cm
C.12cm
D.16cm
2.如图,平行四边形ABCD的周长为40,△BOC的周长比△AOB的周长多10,则BC长为( )
A.20
B.5
C.10
D.15
3.如图,Rt△ABC中,∠BAC=90°,AC=6,∠ACB=30°,点P为BC上任意一点,连接PA,以PA、PC为邻边作平行四边形PAQC,连接PQ,与AC交于点O,则PQ的最小值为( )
A.1
B.2
C.3
D.4
4.如图,在?ABCD中,AB=3,AD=5,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=( )
A.1
B.
C.2
D.3
5.如图,已知平行四边形ABCD中,点A的坐标是(4,0),点C的坐标是(﹣4,0),点D的坐标是(﹣2,﹣2),则点B的坐标是( )
A.(4,2)
B.(6,﹣2)
C.(2,2)
D.(﹣10,﹣2)
6.如图,?ABCD的周长为60cm,AC,BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
A.30
cm
B.60cm
C.40cm
D.20
cm
7.?ABCD一内角的平分线与边相交并把这条边分成2cm,3cm的两条线段,则?ABCD的周长是( )
A.5cm
B.7cm
C.14cm或15cm
D.14cm或16cm
8.如图,点A在平行四边形的对角线上,试判断S1,S2之间的大小关系( )
A.S1=S2
B.S1>S2
C.S1<S2
D.无法确定
9.点A,B,C,D在同一平面内,从四个条件中(1)AB=CD,(2)AB∥CD,(3)BC=AD,(4)BC∥AD中任选两个,使四边形ABCD是平行四边形,这样的选法有( )
A.3种
B.4种
C.5种
D.6种
10.在长方形ABCD中,AB=,BC=4,CE=CF,延长AB至点E,连接CE,CF平分∠ECD,则BE=
.
11.如图,AC是菱形ABCD的对角线,P是AC上的一个动点,过点P分别作AB和BC的垂线,垂足分别是点F和E,若菱形的周长是12cm,面积是6cm2,则PE+PF的值是
cm.
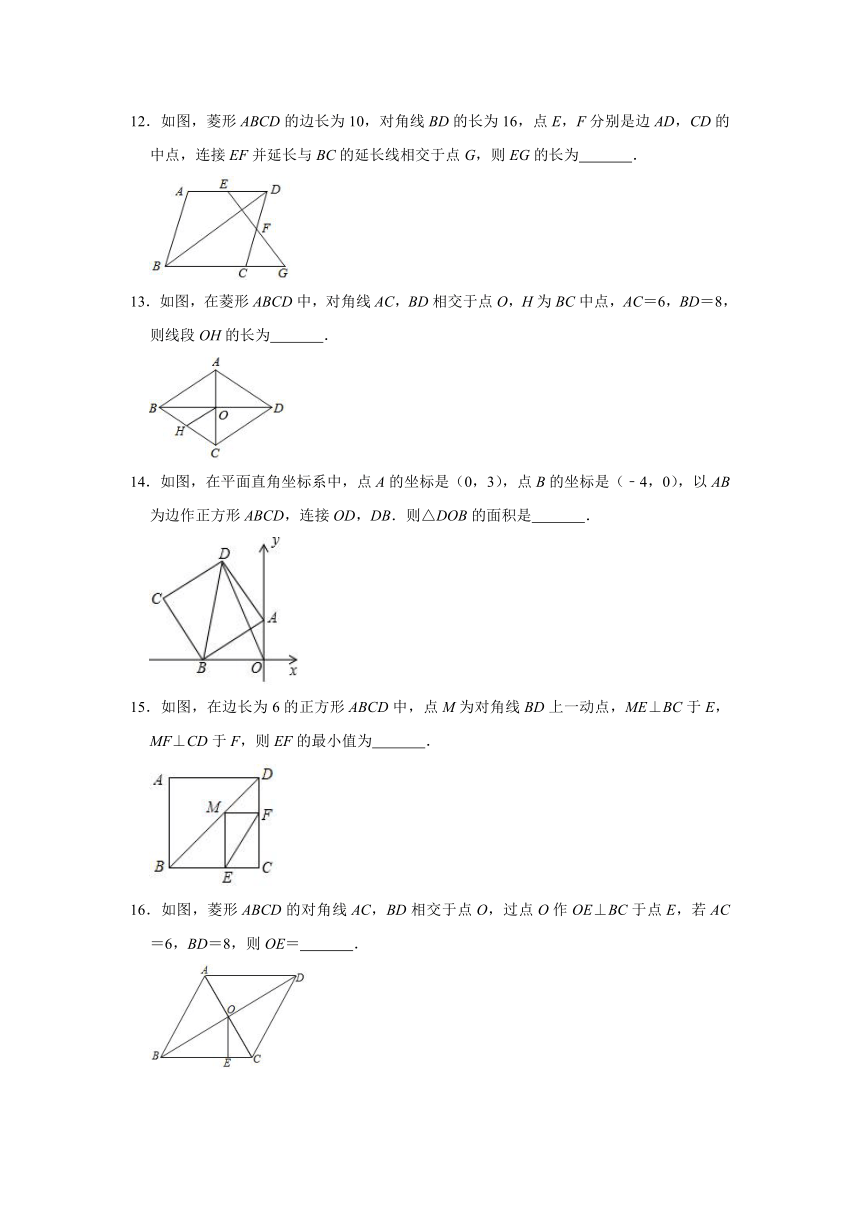
12.如图,菱形ABCD的边长为10,对角线BD的长为16,点E,F分别是边AD,CD的中点,连接EF并延长与BC的延长线相交于点G,则EG的长为
.
13.如图,在菱形ABCD中,对角线AC,BD相交于点O,H为BC中点,AC=6,BD=8,则线段OH的长为
.
14.如图,在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(﹣4,0),以AB为边作正方形ABCD,连接OD,DB.则△DOB的面积是
.
15.如图,在边长为6的正方形ABCD中,点M为对角线BD上一动点,ME⊥BC于E,MF⊥CD于F,则EF的最小值为
.
16.如图,菱形ABCD的对角线AC,BD相交于点O,过点O作OE⊥BC于点E,若AC=6,BD=8,则OE=
.
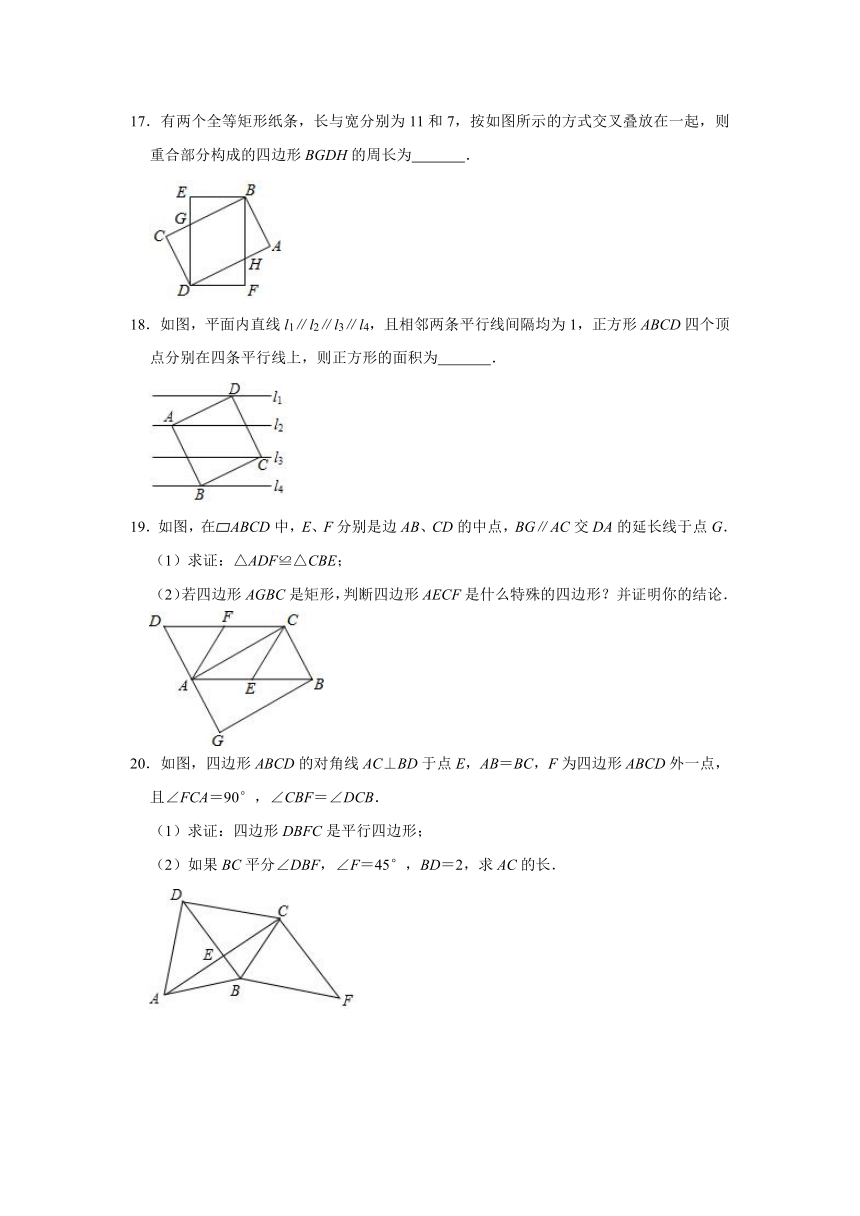
17.有两个全等矩形纸条,长与宽分别为11和7,按如图所示的方式交叉叠放在一起,则重合部分构成的四边形BGDH的周长为
.
18.如图,平面内直线l1∥l2∥l3∥l4,且相邻两条平行线间隔均为1,正方形ABCD四个顶点分别在四条平行线上,则正方形的面积为
.
19.如图,在?ABCD中,E、F分别是边AB、CD的中点,BG∥AC交DA的延长线于点G.
(1)求证:△ADF≌△CBE;
(2)若四边形AGBC是矩形,判断四边形AECF是什么特殊的四边形?并证明你的结论.
20.如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠F=45°,BD=2,求AC的长.
21.如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:BF=BC;
(2)若∠AFC=2∠D,连接AC,BE,求证:四边形ABEC是矩形.
22.如图,在?ABCD中,对角线AC、BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
23.如图,在△ABC中,点D为边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在AB上,且BF=DE.
(1)求证:四边形BDEF是平行四边形;
(2)线段AB,BF,AC之间具有怎样的数量关系?证明你所得到的结论.
24.正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连接CE.
(1)已知点F在线段BC上
①若AB=BE,求∠DAE度数;
②求证:CE=EF
(2)已知正方形边长为2,且BC=2BF,请直接写出线段DE的长.
25.正方形ABCD中,点P是边CD上的任意一点,连接BP,O为BP的中点,作PE⊥BD于E,连接EO,AE.
(1)若∠PBC=α,求∠POE的大小(用含α的式子表示);
(2)用等式表示线段AE与BP之间的数量关系,并证明.
26.如图,在平行四边形ABCD中,CE⊥BC交AD于点E,连接BE,点F是BE上一点,连接CF.
(1)如图1,若∠ECD=30°,BC=BF=4,DC=2,求EF的长;
(2)如图2,若BC=EC,过点E作EM⊥CF,交CF延长线于点M,延长ME、CD相交于点G,连接BG交CM于点N,若CM=MG,求证:EG=2MN.
参考答案
1.解:由题意可知,平行四边形边长的取值范围是:8﹣3<边长<8+3,即5<边长<11.
只有选项B在此范围内,故选B.
2.解:∵△BOC的周长比△AOB的周长多10,
∴BC﹣AB=10,①
∵平行四边形ABCD的周长为40,
∴BC+AB=20,②
由①+②,可得2BC=30,
∴BC=15.
故选:D.
3.解:∵∠BAC=90°,AC=6,∠ACB=30°,
∴AB=2,BC=4,
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO,
∵PQ最短也就是PO最短,
∴过O作BC的垂线OP′,
∵∠ACB=∠P′CO,∠CP′O=∠CAB=90°,
∴△CAB∽△CP′O,
∴=,
∴=,
∴OP′=,
∴则PQ的最小值为2OP′=3.
故选:C.
4.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC=5,AB=CD=3,
∴∠ABE=∠CFE,
∵∠ABC的平分线交AD于点E,
∴∠ABE=∠CBF,
∴∠CBF=∠CFB,
∴CF=CB=5,
∴DF=CF﹣CD=5﹣3=2,
故选:C.
5.解:如图所示,平行四边形ABCD中,点A的坐标是(4,0),点C的坐标是(﹣4,0),
∴O是AC的中点,
∴点D与点B关于原点对称,
又∵点D的坐标是(﹣2,﹣2),
∴B(2,2),
故选:C.
6.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OB=OD,
又∵OE⊥BD,
∴OE是线段BD的中垂线,
∴BE=DE,
∴AE+ED=AE+BE,
∵?ABCD的周长为60cm,
∴AB+AD=30cm,
∴△ABE的周长=AB+AE+BE=AB+AD=30cm,
故选:A.
7.解:AE平分平行四边形ABCD一内角∠DAB.
如图1,当BE=2cm,CE=3cm时,
∵AE平分∠BAD,
∴∠BAE=∠EAD.
∵AD∥BC,
∴∠DAE=∠AEB.
∴∠BAE=∠AEB.
∴BA=BE=2cm.
∴平行四边形周长为2×(2+5)=14cm;
如图2,当CE=2cm,BE=3cm时,
同理可得BA=BE=3cm.
则平行四边形周长为2×(3+5)=16cm.
综上所述平行四边形ABCD周长为14cm或16cm.
故选:D.
8.解:如图,作EM⊥FH,GN⊥FH,
S1=FA?EM,S2=FA?GN
根据△EFH与△GFH的面积相等,可得EM=GN,
∴S1=S2.
故选:A.
9.解:任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有(1)(2);(3)(4);(1)(3);(2)(4)共四种.
故选:B.
10.解:如图,延长CF,BA交于点G,连接EF,过点F作FH⊥CE于H,过点E作EM⊥CF于M,
∵四边形ABCD是矩形,且AB=,BC=4,
∴AB∥CD,AB=CD=,∠D=∠ABC=∠CBE=90°,
∴∠DCF=∠G,
∵CF平分∠ECD,
∴∠DCF=∠FCE,FH=DF,
∴∠G=∠ECF,
∴EC=EG,
∴∠ECG是等腰三角形,
∴CM=MG,
∵CE=CF,
∴△ECF是等腰三角形,
∵EM⊥CF,FH⊥CE,
∴EM和FH是等腰三角形腰上的高,
∴EM=FH=DF,
∴Rt△CDF≌Rt△CME(HL),
∴CM=CD=,
∴CG=5,
Rt△CBG中,BG===3,
设BE=x,则EC=EG=3+x,
Rt△CBE中,(3+x)2=x2+42,
解得:x=,
∴BE=.
故答案为:.
11.解:连接BP,
(cm2),
∴AB=BC==3(cm),
∴(cm2),
∴,
∴(cm),
故答案为:2.
12.解:连接AC,交BD于点O,如图所示:
∵菱形ABCD的边长为10,
∴AD∥BC,AB=BC=CD=DA=10,
∵点E、F分别是边AD,CD的中点,
∴EF是△ACD的中位线,
∴EF∥AC,
∵AC、BD是菱形的对角线,BD=16,
∴AC⊥BD,OB=OD=8,OA=OC,
又∵AD∥BC,EF∥AC,
∴四边形CAEG是平行四边形,
∴AC=EG,
在Rt△AOB中,AB=10,OB=8,
∴OA=OC==6,
∴AC=2OA=12,
∴EG=AC=12;
故答案为:12.
13.解:∵四边形ABCD为菱形,
∴AC⊥BD,OB=OD=BD=4,OC=OA=AC=3,
在Rt△BOC中,BC===5,
∵H为BC中点,
∴OH=BC=2.5.
故答案为:2.5.
14.解:过点D作DE⊥y轴,垂足为E.
∵A的坐标是(0,3),点B的坐标是(﹣4,0),
∴OA=3,OB=4.
∵ABCD为正方形,
∴AB=AD,∠DAB=90°.
∴∠DAE=∠AB0.
在△ABO和△DAE中,
∴△ABO≌△DAE.
∴AE=OB=4.
∴OE=AE+AO=4+3=7.
∴△OBD的面积=OB?OE=×4×7=14.
故答案为:14.
15.解:连接MC,如图所示:
∵四边形ABCD是正方形,
∴∠C=90°,∠DBC=45°,
∵ME⊥BC于E,MF⊥CD于F,
∴四边形MECF为矩形,
∴EF=MC,
当MC⊥BD时,MC取得最小值,
此时△BCM是等腰直角三角形,
∴MC=BC=×6=3,
∴EF的最小值为3;
故答案为:3.
16.解:∵菱形ABCD中,AC=6,BD=8,
∴OA=OC=AC=3,OB=BD=4,AC⊥BD,
∴BC===5,
∵OE⊥BC,
∴S△OBC=×OB×OC=×BC×OE,
∴OE===,
故答案为:.
17.解:由题意得:矩形ABCD≌矩形BEDF,
∴∠A=90°,AB=BE=7,AD∥BC,BF∥DE,AD=11,
∴四边形BGDH是平行四边形,
∴平行四边形BGDH的面积=BG×AB=BH×BE,
∴BG=BH,
∴四边形BGDH是菱形,
∴BH=DH=DG=BG,
设BH=DH=x,则AH=11﹣x,
在Rt△ABH中,由勾股定理得:72+(11﹣x)2=x2,
解得:x=,
∴BH=,
∴四边形BGDH的周长=4BH=,
故答案为:.
18.解:过C点作EF⊥l2,交l1于E点,交l4于F点.
∵l1∥l2∥l3∥l4,EF⊥l2,
∴EF⊥l1,EF⊥l4,
即∠CED=∠BFC=90°.
∵ABCD为正方形,
∴∠BCD=90°.
∴∠DCE+∠BCF=90°.
又∵∠DCE+∠CDE=90°,
∴∠CDE=∠BCF.
在△CDE和△BCF中,
∴△CDE≌△BCF(AAS),
∴BF=CE=2.
∵CF=1,
∴BC2=12+22=5,
即正方形ABCD的面积为5.
故答案为:5.
19.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠D=∠ABC,AB=CD,
又∵E、F分别是边AB、CD的中点,
∴DF=BE,
在△ADF和△CBE中,
,
∴△ADF∽≌△CBE(SAS);
(2)解:四边形AECF为菱形;理由如下:
∵四边形AGBC是矩形,
∴∠ACB=90°,
又∵E为AB中点,
∴CE=AB=AE,
同理AF=FC,
∴AF=FC=CE=EA,
∴四边形AECF为菱形.
20.(1)证明:∵AC⊥BD,∠FCA=90°,∠CBF=∠DCB.
∴BD∥CF,CD∥BF,
∴四边形DBFC是平行四边形;
(2)解:∵四边形DBFC是平行四边形,
∴CF=BD=2,
∵AB=BC,AC⊥BD,
∴AE=CE,
作CM⊥BF于M,
∵BC平分∠DBF,
∴CE=CM,
∵∠F=45°,
∴△CFM是等腰直角三角形,
∴CM=CF=,
∴AE=CE=,
∴AC=2.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵CE=DC,
∴AB=EC,
∴四边形ABEC是平行四边形,
∴BF=BC;
(2)∵由(1)知,四边形ABEC是平行四边形,
∴FA=FE,FB=FC.
∵四边形ABCD是平行四边形,
∴∠ABC=∠D.
又∵∠AFC=2∠ADC,
∴∠AFC=2∠ABC.
∵∠AFC=∠ABC+∠BAF,
∴∠ABC=∠BAF,
∴FA=FB,
∴FA=FE=FB=FC,
∴AE=BC,
∴四边形ABEC是矩形.
22.证明:(1)∵?ABCD,
∴AO=OC,
∵△ACE是等边三角形,
∴EO⊥AC
(三线合一)
即
BD⊥AC,
∴?ABCD是菱形;
(2)∵△ACE是等边三角形,∠EAC=60°
由(1)知,EO⊥AC,AO=OC
∴∠AEO=∠OEC=30°,△AOE是直角三角形
∴∠EAO=60°,
∵∠AED=2∠EAD,
∴∠EAD=15°,
∴∠DAO=∠EAO﹣∠EAD=45°,
∵?ABCD是菱形,
∴∠BAD=2∠DAO=90°,
∴菱形ABCD是正方形.
23.(1)证明:延长CE交AB于点G,
∵AE⊥CE,
∴∠AEG=∠AEC=90°,
在△AEG和△AEC中,
,
∴△AGE≌△ACE(ASA).
∴GE=EC.
∵BD=CD,
∴DE为△CGB的中位线,
∴DE∥AB.
∵DE=BF,
∴四边形BDEF是平行四边形.
(2)解:BF=(AB﹣AC).
理由如下:
∵四边形BDEF是平行四边形,
∴BF=DE.
∵D、E分别是BC、GC的中点,
∴BF=DE=BG.
∵△AGE≌△ACE,
∴AG=AC,
∴BF=(AB﹣AG)=(AB﹣AC).
24.解:(1)①∵ABCD为正方形,
∴∠ABE=45°.
又∵AB=BE,
∴∠BAE=×(180°﹣45°)=67.5°.
∴∠DAE=90°﹣67.5°=22.5°
②证明:∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABC=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF.
(2)如下图所示:过点E作MN⊥BC,垂足为N,交AD于M.
∵CE=EF,
∴N是CF的中点.
∵BC=2BF,
∴=.
又∵四边形CDMN是矩形,△DME为等腰直角三角形,
∴CN=DM=ME,
∴ED=DM=CN=.
如下图所示:过点E作MN⊥BC,垂足为N,交AD于M.
∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABF=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF.
∴FN=CN.
又∵BC=2BF,
∴FC=3,
∴CN=,
∴EN=BN=,
∴DE=.
综上所述,ED的长为或
25.解:(1)在正方形ABCD中,BC=DC,∠C=90°,
∴∠DBC=∠CDB=45°,
∵∠PBC=α,
∴∠DBP=45°﹣α,
∵PE⊥BD,且O为BP的中点,
∴EO=BO,
∴∠EBO=∠BEO,
∴∠EOP=∠EBO+∠BEO=90°﹣2
α;
(2)BP=.证明如下:
连接OC,EC,
在正方形ABCD中,AB=BC,∠ABD=∠CBD,BE=BE,
∴△ABE≌△CBE(SAS),
∴AE=CE,
设∠PBC=α,
在Rt△BPC中,O为BP的中点,
∴CO=BO=,
∴∠OBC=∠OCB,
∴∠COP=2
α,
由(1)知∠EOP=90°﹣2α,
∴∠EOC=∠COP+∠EOP=90°,
又由(1)知BO=EO,
∴EO=CO.
∴△EOC是等腰直角三角形,
∴EO2+OC2=EC2,
∴EC=OC=,
即BP=,
∴BP=.
26.(1)解:如图1中,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵EC⊥BC,
∴AD⊥EC,
∴∠BCE=∠CED=90°,
∵∠ECD=30°,CD=2,
∴CE=CD?cos30°=,
在Rt△BCE中,BE==,
∵BC=BF=4,
∴EF=BE﹣BF=﹣4.
(2)证明:如图2中,延长GM到H,使得MH=MG,连接CH,BH.
∵CM=MG=MH,CM⊥GH,
∴∠HCG=90°,CH=CG,
∴∠HCG=∠BCE,
∴∠BCH=∠ECG,
∵CB=CE,
∴△BCH≌△ECG(SAS),
∴BH=EG,∠CHB=∠CGE=45°,
∵∠CHG=45°,
∴∠BHG=90°,
∴∠BHG=∠CMG=90°,
∴MN∥BH,∵HM=MG,
∴BN=NG,
∴BH=2MN,
∴EG=2MN.
1.若平行四边形的两条对角线长为6
cm和16
cm,则下列长度的线段可作为平行四边形边长的是( )
A.5cm
B.8cm
C.12cm
D.16cm
2.如图,平行四边形ABCD的周长为40,△BOC的周长比△AOB的周长多10,则BC长为( )
A.20
B.5
C.10
D.15
3.如图,Rt△ABC中,∠BAC=90°,AC=6,∠ACB=30°,点P为BC上任意一点,连接PA,以PA、PC为邻边作平行四边形PAQC,连接PQ,与AC交于点O,则PQ的最小值为( )
A.1
B.2
C.3
D.4
4.如图,在?ABCD中,AB=3,AD=5,∠ABC的平分线交AD于E,交CD的延长线于点F,则DF=( )
A.1
B.
C.2
D.3
5.如图,已知平行四边形ABCD中,点A的坐标是(4,0),点C的坐标是(﹣4,0),点D的坐标是(﹣2,﹣2),则点B的坐标是( )
A.(4,2)
B.(6,﹣2)
C.(2,2)
D.(﹣10,﹣2)
6.如图,?ABCD的周长为60cm,AC,BD相交于点O,EO⊥BD交AD于点E,则△ABE的周长为( )
A.30
cm
B.60cm
C.40cm
D.20
cm
7.?ABCD一内角的平分线与边相交并把这条边分成2cm,3cm的两条线段,则?ABCD的周长是( )
A.5cm
B.7cm
C.14cm或15cm
D.14cm或16cm
8.如图,点A在平行四边形的对角线上,试判断S1,S2之间的大小关系( )
A.S1=S2
B.S1>S2
C.S1<S2
D.无法确定
9.点A,B,C,D在同一平面内,从四个条件中(1)AB=CD,(2)AB∥CD,(3)BC=AD,(4)BC∥AD中任选两个,使四边形ABCD是平行四边形,这样的选法有( )
A.3种
B.4种
C.5种
D.6种
10.在长方形ABCD中,AB=,BC=4,CE=CF,延长AB至点E,连接CE,CF平分∠ECD,则BE=
.
11.如图,AC是菱形ABCD的对角线,P是AC上的一个动点,过点P分别作AB和BC的垂线,垂足分别是点F和E,若菱形的周长是12cm,面积是6cm2,则PE+PF的值是
cm.
12.如图,菱形ABCD的边长为10,对角线BD的长为16,点E,F分别是边AD,CD的中点,连接EF并延长与BC的延长线相交于点G,则EG的长为
.
13.如图,在菱形ABCD中,对角线AC,BD相交于点O,H为BC中点,AC=6,BD=8,则线段OH的长为
.
14.如图,在平面直角坐标系中,点A的坐标是(0,3),点B的坐标是(﹣4,0),以AB为边作正方形ABCD,连接OD,DB.则△DOB的面积是
.
15.如图,在边长为6的正方形ABCD中,点M为对角线BD上一动点,ME⊥BC于E,MF⊥CD于F,则EF的最小值为
.
16.如图,菱形ABCD的对角线AC,BD相交于点O,过点O作OE⊥BC于点E,若AC=6,BD=8,则OE=
.
17.有两个全等矩形纸条,长与宽分别为11和7,按如图所示的方式交叉叠放在一起,则重合部分构成的四边形BGDH的周长为
.
18.如图,平面内直线l1∥l2∥l3∥l4,且相邻两条平行线间隔均为1,正方形ABCD四个顶点分别在四条平行线上,则正方形的面积为
.
19.如图,在?ABCD中,E、F分别是边AB、CD的中点,BG∥AC交DA的延长线于点G.
(1)求证:△ADF≌△CBE;
(2)若四边形AGBC是矩形,判断四边形AECF是什么特殊的四边形?并证明你的结论.
20.如图,四边形ABCD的对角线AC⊥BD于点E,AB=BC,F为四边形ABCD外一点,且∠FCA=90°,∠CBF=∠DCB.
(1)求证:四边形DBFC是平行四边形;
(2)如果BC平分∠DBF,∠F=45°,BD=2,求AC的长.
21.如图,将?ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
(1)求证:BF=BC;
(2)若∠AFC=2∠D,连接AC,BE,求证:四边形ABEC是矩形.
22.如图,在?ABCD中,对角线AC、BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若∠AED=2∠EAD,求证:四边形ABCD是正方形.
23.如图,在△ABC中,点D为边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在AB上,且BF=DE.
(1)求证:四边形BDEF是平行四边形;
(2)线段AB,BF,AC之间具有怎样的数量关系?证明你所得到的结论.
24.正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连接CE.
(1)已知点F在线段BC上
①若AB=BE,求∠DAE度数;
②求证:CE=EF
(2)已知正方形边长为2,且BC=2BF,请直接写出线段DE的长.
25.正方形ABCD中,点P是边CD上的任意一点,连接BP,O为BP的中点,作PE⊥BD于E,连接EO,AE.
(1)若∠PBC=α,求∠POE的大小(用含α的式子表示);
(2)用等式表示线段AE与BP之间的数量关系,并证明.
26.如图,在平行四边形ABCD中,CE⊥BC交AD于点E,连接BE,点F是BE上一点,连接CF.
(1)如图1,若∠ECD=30°,BC=BF=4,DC=2,求EF的长;
(2)如图2,若BC=EC,过点E作EM⊥CF,交CF延长线于点M,延长ME、CD相交于点G,连接BG交CM于点N,若CM=MG,求证:EG=2MN.
参考答案
1.解:由题意可知,平行四边形边长的取值范围是:8﹣3<边长<8+3,即5<边长<11.
只有选项B在此范围内,故选B.
2.解:∵△BOC的周长比△AOB的周长多10,
∴BC﹣AB=10,①
∵平行四边形ABCD的周长为40,
∴BC+AB=20,②
由①+②,可得2BC=30,
∴BC=15.
故选:D.
3.解:∵∠BAC=90°,AC=6,∠ACB=30°,
∴AB=2,BC=4,
∵四边形APCQ是平行四边形,
∴PO=QO,CO=AO,
∵PQ最短也就是PO最短,
∴过O作BC的垂线OP′,
∵∠ACB=∠P′CO,∠CP′O=∠CAB=90°,
∴△CAB∽△CP′O,
∴=,
∴=,
∴OP′=,
∴则PQ的最小值为2OP′=3.
故选:C.
4.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD=BC=5,AB=CD=3,
∴∠ABE=∠CFE,
∵∠ABC的平分线交AD于点E,
∴∠ABE=∠CBF,
∴∠CBF=∠CFB,
∴CF=CB=5,
∴DF=CF﹣CD=5﹣3=2,
故选:C.
5.解:如图所示,平行四边形ABCD中,点A的坐标是(4,0),点C的坐标是(﹣4,0),
∴O是AC的中点,
∴点D与点B关于原点对称,
又∵点D的坐标是(﹣2,﹣2),
∴B(2,2),
故选:C.
6.解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OB=OD,
又∵OE⊥BD,
∴OE是线段BD的中垂线,
∴BE=DE,
∴AE+ED=AE+BE,
∵?ABCD的周长为60cm,
∴AB+AD=30cm,
∴△ABE的周长=AB+AE+BE=AB+AD=30cm,
故选:A.
7.解:AE平分平行四边形ABCD一内角∠DAB.
如图1,当BE=2cm,CE=3cm时,
∵AE平分∠BAD,
∴∠BAE=∠EAD.
∵AD∥BC,
∴∠DAE=∠AEB.
∴∠BAE=∠AEB.
∴BA=BE=2cm.
∴平行四边形周长为2×(2+5)=14cm;
如图2,当CE=2cm,BE=3cm时,
同理可得BA=BE=3cm.
则平行四边形周长为2×(3+5)=16cm.
综上所述平行四边形ABCD周长为14cm或16cm.
故选:D.
8.解:如图,作EM⊥FH,GN⊥FH,
S1=FA?EM,S2=FA?GN
根据△EFH与△GFH的面积相等,可得EM=GN,
∴S1=S2.
故选:A.
9.解:任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有(1)(2);(3)(4);(1)(3);(2)(4)共四种.
故选:B.
10.解:如图,延长CF,BA交于点G,连接EF,过点F作FH⊥CE于H,过点E作EM⊥CF于M,
∵四边形ABCD是矩形,且AB=,BC=4,
∴AB∥CD,AB=CD=,∠D=∠ABC=∠CBE=90°,
∴∠DCF=∠G,
∵CF平分∠ECD,
∴∠DCF=∠FCE,FH=DF,
∴∠G=∠ECF,
∴EC=EG,
∴∠ECG是等腰三角形,
∴CM=MG,
∵CE=CF,
∴△ECF是等腰三角形,
∵EM⊥CF,FH⊥CE,
∴EM和FH是等腰三角形腰上的高,
∴EM=FH=DF,
∴Rt△CDF≌Rt△CME(HL),
∴CM=CD=,
∴CG=5,
Rt△CBG中,BG===3,
设BE=x,则EC=EG=3+x,
Rt△CBE中,(3+x)2=x2+42,
解得:x=,
∴BE=.
故答案为:.
11.解:连接BP,
(cm2),
∴AB=BC==3(cm),
∴(cm2),
∴,
∴(cm),
故答案为:2.
12.解:连接AC,交BD于点O,如图所示:
∵菱形ABCD的边长为10,
∴AD∥BC,AB=BC=CD=DA=10,
∵点E、F分别是边AD,CD的中点,
∴EF是△ACD的中位线,
∴EF∥AC,
∵AC、BD是菱形的对角线,BD=16,
∴AC⊥BD,OB=OD=8,OA=OC,
又∵AD∥BC,EF∥AC,
∴四边形CAEG是平行四边形,
∴AC=EG,
在Rt△AOB中,AB=10,OB=8,
∴OA=OC==6,
∴AC=2OA=12,
∴EG=AC=12;
故答案为:12.
13.解:∵四边形ABCD为菱形,
∴AC⊥BD,OB=OD=BD=4,OC=OA=AC=3,
在Rt△BOC中,BC===5,
∵H为BC中点,
∴OH=BC=2.5.
故答案为:2.5.
14.解:过点D作DE⊥y轴,垂足为E.
∵A的坐标是(0,3),点B的坐标是(﹣4,0),
∴OA=3,OB=4.
∵ABCD为正方形,
∴AB=AD,∠DAB=90°.
∴∠DAE=∠AB0.
在△ABO和△DAE中,
∴△ABO≌△DAE.
∴AE=OB=4.
∴OE=AE+AO=4+3=7.
∴△OBD的面积=OB?OE=×4×7=14.
故答案为:14.
15.解:连接MC,如图所示:
∵四边形ABCD是正方形,
∴∠C=90°,∠DBC=45°,
∵ME⊥BC于E,MF⊥CD于F,
∴四边形MECF为矩形,
∴EF=MC,
当MC⊥BD时,MC取得最小值,
此时△BCM是等腰直角三角形,
∴MC=BC=×6=3,
∴EF的最小值为3;
故答案为:3.
16.解:∵菱形ABCD中,AC=6,BD=8,
∴OA=OC=AC=3,OB=BD=4,AC⊥BD,
∴BC===5,
∵OE⊥BC,
∴S△OBC=×OB×OC=×BC×OE,
∴OE===,
故答案为:.
17.解:由题意得:矩形ABCD≌矩形BEDF,
∴∠A=90°,AB=BE=7,AD∥BC,BF∥DE,AD=11,
∴四边形BGDH是平行四边形,
∴平行四边形BGDH的面积=BG×AB=BH×BE,
∴BG=BH,
∴四边形BGDH是菱形,
∴BH=DH=DG=BG,
设BH=DH=x,则AH=11﹣x,
在Rt△ABH中,由勾股定理得:72+(11﹣x)2=x2,
解得:x=,
∴BH=,
∴四边形BGDH的周长=4BH=,
故答案为:.
18.解:过C点作EF⊥l2,交l1于E点,交l4于F点.
∵l1∥l2∥l3∥l4,EF⊥l2,
∴EF⊥l1,EF⊥l4,
即∠CED=∠BFC=90°.
∵ABCD为正方形,
∴∠BCD=90°.
∴∠DCE+∠BCF=90°.
又∵∠DCE+∠CDE=90°,
∴∠CDE=∠BCF.
在△CDE和△BCF中,
∴△CDE≌△BCF(AAS),
∴BF=CE=2.
∵CF=1,
∴BC2=12+22=5,
即正方形ABCD的面积为5.
故答案为:5.
19.(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,∠D=∠ABC,AB=CD,
又∵E、F分别是边AB、CD的中点,
∴DF=BE,
在△ADF和△CBE中,
,
∴△ADF∽≌△CBE(SAS);
(2)解:四边形AECF为菱形;理由如下:
∵四边形AGBC是矩形,
∴∠ACB=90°,
又∵E为AB中点,
∴CE=AB=AE,
同理AF=FC,
∴AF=FC=CE=EA,
∴四边形AECF为菱形.
20.(1)证明:∵AC⊥BD,∠FCA=90°,∠CBF=∠DCB.
∴BD∥CF,CD∥BF,
∴四边形DBFC是平行四边形;
(2)解:∵四边形DBFC是平行四边形,
∴CF=BD=2,
∵AB=BC,AC⊥BD,
∴AE=CE,
作CM⊥BF于M,
∵BC平分∠DBF,
∴CE=CM,
∵∠F=45°,
∴△CFM是等腰直角三角形,
∴CM=CF=,
∴AE=CE=,
∴AC=2.
21.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵CE=DC,
∴AB=EC,
∴四边形ABEC是平行四边形,
∴BF=BC;
(2)∵由(1)知,四边形ABEC是平行四边形,
∴FA=FE,FB=FC.
∵四边形ABCD是平行四边形,
∴∠ABC=∠D.
又∵∠AFC=2∠ADC,
∴∠AFC=2∠ABC.
∵∠AFC=∠ABC+∠BAF,
∴∠ABC=∠BAF,
∴FA=FB,
∴FA=FE=FB=FC,
∴AE=BC,
∴四边形ABEC是矩形.
22.证明:(1)∵?ABCD,
∴AO=OC,
∵△ACE是等边三角形,
∴EO⊥AC
(三线合一)
即
BD⊥AC,
∴?ABCD是菱形;
(2)∵△ACE是等边三角形,∠EAC=60°
由(1)知,EO⊥AC,AO=OC
∴∠AEO=∠OEC=30°,△AOE是直角三角形
∴∠EAO=60°,
∵∠AED=2∠EAD,
∴∠EAD=15°,
∴∠DAO=∠EAO﹣∠EAD=45°,
∵?ABCD是菱形,
∴∠BAD=2∠DAO=90°,
∴菱形ABCD是正方形.
23.(1)证明:延长CE交AB于点G,
∵AE⊥CE,
∴∠AEG=∠AEC=90°,
在△AEG和△AEC中,
,
∴△AGE≌△ACE(ASA).
∴GE=EC.
∵BD=CD,
∴DE为△CGB的中位线,
∴DE∥AB.
∵DE=BF,
∴四边形BDEF是平行四边形.
(2)解:BF=(AB﹣AC).
理由如下:
∵四边形BDEF是平行四边形,
∴BF=DE.
∵D、E分别是BC、GC的中点,
∴BF=DE=BG.
∵△AGE≌△ACE,
∴AG=AC,
∴BF=(AB﹣AG)=(AB﹣AC).
24.解:(1)①∵ABCD为正方形,
∴∠ABE=45°.
又∵AB=BE,
∴∠BAE=×(180°﹣45°)=67.5°.
∴∠DAE=90°﹣67.5°=22.5°
②证明:∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABC=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF.
(2)如下图所示:过点E作MN⊥BC,垂足为N,交AD于M.
∵CE=EF,
∴N是CF的中点.
∵BC=2BF,
∴=.
又∵四边形CDMN是矩形,△DME为等腰直角三角形,
∴CN=DM=ME,
∴ED=DM=CN=.
如下图所示:过点E作MN⊥BC,垂足为N,交AD于M.
∵正方形ABCD关于BD对称,
∴△ABE≌△CBE,
∴∠BAE=∠BCE.
又∵∠ABF=∠AEF=90°,
∴∠BAE=∠EFC,
∴∠BCE=∠EFC,
∴CE=EF.
∴FN=CN.
又∵BC=2BF,
∴FC=3,
∴CN=,
∴EN=BN=,
∴DE=.
综上所述,ED的长为或
25.解:(1)在正方形ABCD中,BC=DC,∠C=90°,
∴∠DBC=∠CDB=45°,
∵∠PBC=α,
∴∠DBP=45°﹣α,
∵PE⊥BD,且O为BP的中点,
∴EO=BO,
∴∠EBO=∠BEO,
∴∠EOP=∠EBO+∠BEO=90°﹣2
α;
(2)BP=.证明如下:
连接OC,EC,
在正方形ABCD中,AB=BC,∠ABD=∠CBD,BE=BE,
∴△ABE≌△CBE(SAS),
∴AE=CE,
设∠PBC=α,
在Rt△BPC中,O为BP的中点,
∴CO=BO=,
∴∠OBC=∠OCB,
∴∠COP=2
α,
由(1)知∠EOP=90°﹣2α,
∴∠EOC=∠COP+∠EOP=90°,
又由(1)知BO=EO,
∴EO=CO.
∴△EOC是等腰直角三角形,
∴EO2+OC2=EC2,
∴EC=OC=,
即BP=,
∴BP=.
26.(1)解:如图1中,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵EC⊥BC,
∴AD⊥EC,
∴∠BCE=∠CED=90°,
∵∠ECD=30°,CD=2,
∴CE=CD?cos30°=,
在Rt△BCE中,BE==,
∵BC=BF=4,
∴EF=BE﹣BF=﹣4.
(2)证明:如图2中,延长GM到H,使得MH=MG,连接CH,BH.
∵CM=MG=MH,CM⊥GH,
∴∠HCG=90°,CH=CG,
∴∠HCG=∠BCE,
∴∠BCH=∠ECG,
∵CB=CE,
∴△BCH≌△ECG(SAS),
∴BH=EG,∠CHB=∠CGE=45°,
∵∠CHG=45°,
∴∠BHG=90°,
∴∠BHG=∠CMG=90°,
∴MN∥BH,∵HM=MG,
∴BN=NG,
∴BH=2MN,
∴EG=2MN.
