2020-2021学年七年级数学北师大版下册 第二章 相交线与平行线 习题练习三(附答案)
文档属性
| 名称 | 2020-2021学年七年级数学北师大版下册 第二章 相交线与平行线 习题练习三(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 89.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 18:08:21 | ||
图片预览




文档简介
七年级数学下册北师大版
第二章
相交线与平行线
习题练习三(附答案)
一、选择题
1.如图所示,有下列五种说法:①∠1和∠4是同位角;②∠3和∠5是内错角;③∠2和∠6是同旁内角;④∠5和∠2是同位角;⑤∠1和∠3是同旁内角;其中正确的是( )
A.
①②③
B.
①②③④
C.
①②③④⑤
D.
①②④⑤
2.下列哪种方法不能检验直线与水平面是否垂直( )
A.
铅垂线
B.
两块三角尺
C.
长方形纸片
D.
合页型折纸
3.如图是五条胡同的路线图(A→B→C→D→E→F),经过测量得到∠B=∠C=70°,∠D=∠E=110°,则图中互相平行的线有( )
A.
1对B.
2对C.
3对D.
4对
4.小明在生日宴会上,要把一个大蛋糕分成七块,问他最少要切几次(切割成的蛋糕面积不一定相等)( )
A.
3次B.
4次C.
5次D.
6次
5.某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.
第一次左拐30°,第二次右拐30°
B.
第一次右拐50°,第二次左拐130°
C.
第一次右拐50°,第二次右拐130°
D.
第一次向左拐50°,第二次向左拐120°
6.如图,AB∥CD,则下列等式成立的是( )
A.
∠B+∠F+∠D=∠E+∠G
B.
∠E+∠F+∠G=∠B+∠D
C.
∠F+∠G+∠D=∠B+∠E
D.
∠B+∠E+∠F=∠G+∠D
7.如图,AB∥EF∥CD,∠ABC=44°,∠CEF=154°,则∠BCE等于( )
A.
22°
B.
18°
C.
20°
D.
26°
8.工人师傅对如图所示的零件进行加工,把材料弯成了一个40°的锐角,然后准备在A处第二次加工拐弯,要保证弯过来的部分与BC保持平行,弯的角度是( )
A.
40°
B.
140°
C.
40°或140°
D.
50°
9.同学们,你一定练过跳远吧!在测量跳远成绩时,从落地点拉向起跳线的皮尺,应当与起跳线( )
A.
平行B.
垂直C.
成45°D.
以上都不对
二、填空题
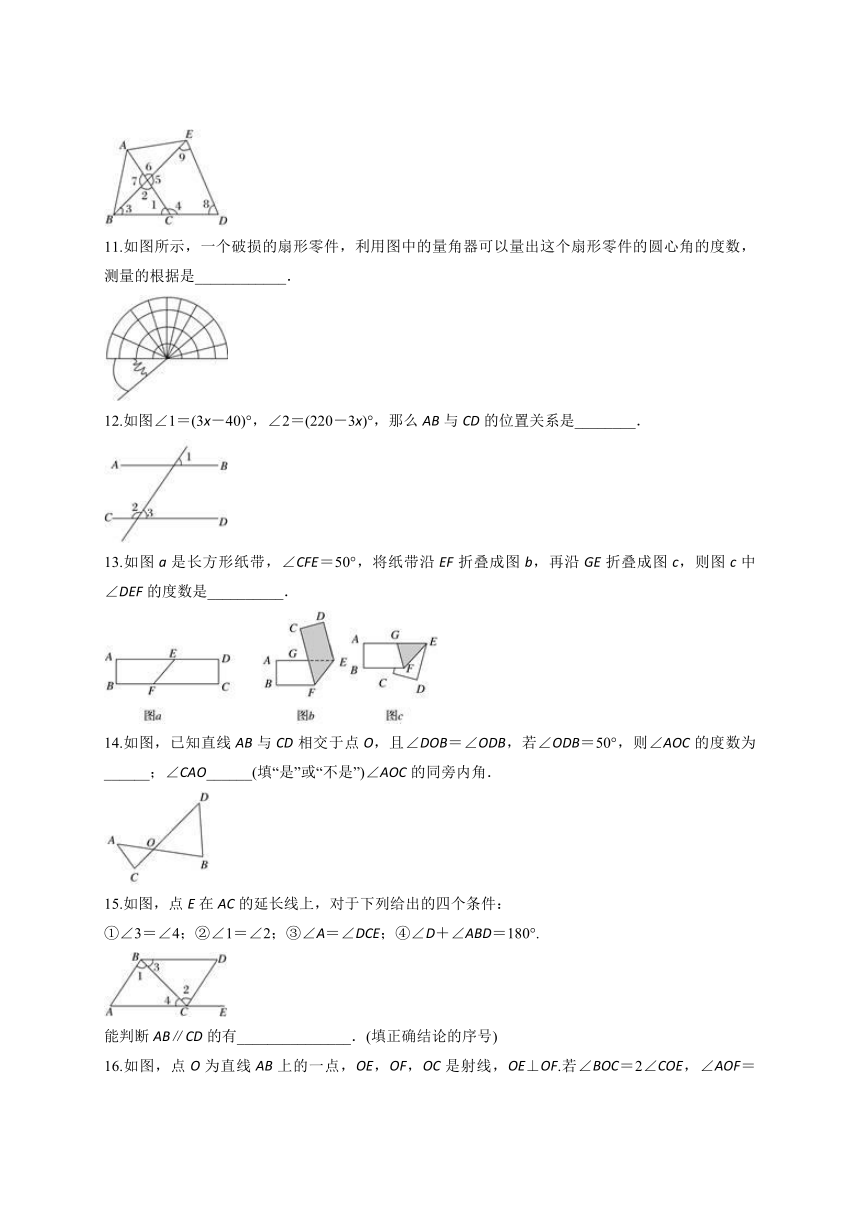
10.如图,与∠2互为同旁内角的是________;与∠3互为同位角的是________;∠6与∠9是______,它们是直线________与______被直线______所截得的;∠3与∠5是直线______与直线______被直线______所截得的;与∠1是同位角的有______,在标有数字的九个角中,大小一定相等的角有__________________.
11.如图所示,一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数,测量的根据是____________.
12.如图∠1=(3x-40)°,∠2=(220-3x)°,那么AB与CD的位置关系是________.
13.如图a是长方形纸带,∠CFE=50°,将纸带沿EF折叠成图b,再沿GE折叠成图c,则图c中∠DEF的度数是__________.
14.如图,已知直线AB与CD相交于点O,且∠DOB=∠ODB,若∠ODB=50°,则∠AOC的度数为______;∠CAO______(填“是”或“不是”)∠AOC的同旁内角.
15.如图,点E在AC的延长线上,对于下列给出的四个条件:
①∠3=∠4;②∠1=∠2;③∠A=∠DCE;④∠D+∠ABD=180°.
能判断AB∥CD的有_______________.(填正确结论的序号)
16.如图,点O为直线AB上的一点,OE,OF,OC是射线,OE⊥OF.若∠BOC=2∠COE,∠AOF=48°,求∠EOC的度数为_________.
17.如图,已知∠MDF=∠B,要得到AB∥CD,则需要添加的条件是:____________.
18.如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第________秒时,边CD恰好与边AB平行.
三、解答题
19.(1)如图1,已知∠B+∠BED+∠D=360°,求证AB∥CD.
(2)如图2,已知∠BED=∠B+∠D,求证AB∥CD.
20.如图,已知∠AOB=40°,画射线OC⊥OA,射线OD⊥OB,画出所有可能的情形并分别求出∠COD的度数.
21.如图所示,直线AB、CD相交于O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.
22.如图,某工程队从A点出发,沿北偏西67度方向修一条公路AD,在BD路段出现塌陷区,就改变方向,由B点沿北偏东23度的方向继续修建BC段,到达C点又改变方向,使所修路段CE∥AB,此时∠ECB有多少度?试说明理由.
23.如图EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
24.已知AB∥CD.
(1)如图①,若∠ABE=30°,∠BEC=148°,求∠ECD的度数;
(2)如图②,若CF∥EB,CF平分∠ECD,试探究∠ECD与∠ABE之间的数量关系,并证明.
答案解析
1.【答案】D
【解析】根据内错角、同位角以及同旁内角的定义分析五种说法.
①∠1和∠4是同位角,即①成立;
②∠3和∠5是内错角,即②成立;
③∠2和∠6是内错角,即③不成立;
④∠5和∠2是同位角,即④成立;
⑤∠1和∠3是同旁内角,即⑤成立.
故选D.
2.【答案】C
【解析】A.根据重力学原理,铅垂线垂直于水平面;
B.将两块三角板的直角边重合,另外两条直角边相交,放在水平面上,可判断重合的直角边垂直于水平面;
C.长方形纸片只能判断长与宽互相垂直,不能判断与水平面垂直;
D.合页型折纸其折痕与纸被折断的一边垂直,即折痕与被折断的两线段垂直,把两放到水平面上,可判断折痕与水平面垂直;故选C.
3.【答案】D
【解析】∵∠B=∠C=70°,∴AB∥CD.
∵∠D=∠E=110°,∴CD∥EF,∴AB∥EF.
∵∠C+∠D=70°+110°=180°,∴BC∥DE.故选D.
4.【答案】A
【解析】设切n次,则+1≥7,解得n≥3或n≤-4(舍去),∴n≥3,故选A.
5.【答案】A
【解析】如图所示(实线为行驶路线):
A符合“同位角相等,两直线平行”的判定,其余均不符合平行线的判定.故选A.
6.【答案】A
【解析】过E作EM∥AB,过F作FH∥AB,过G作GN∥AB,
∵AB∥CD,∴AB∥EM∥GN∥CD∥FH,
∴∠B=∠BEM,∠FEM=∠HFE,∠HFG=∠FGN,∠D=∠NGD,
∴∠B+∠EFH+∠HFG+∠D=∠BEM+∠MEF+∠FGN+∠NGD,
∴∠B+∠EFG+∠D=∠BEF+∠FGD,故选A.
7.【答案】B
【解析】∵AB∥EF∥CD,∠ABC=44°,∠CEF=154°,
∴∠BCD=∠ABC=44°,∠FEC+∠ECD=180°,∴∠ECD=180°-∠FEC=26°,
∴∠BCE=∠BCD-∠ECD=44°-26°=18°.故选B.
8.【答案】C
【解析】如图1,作AE∥BC,则∠CBA=∠EAB=40°;
如图2,作AE∥BC,则∠CBA+∠EAB=180°,
∵∠CBA=40°,∴∠EAB=140°,
综上所述,弯的角度是40°或140°.故选C.
9.【答案】B
【解析】∵点到直线的垂线段的长叫点到直线的距离,
∴在测量跳远成绩时,从落地点拉向起跳线的皮尺,应当与起跳线垂直.故选B.
10.【答案】∠1和∠3 ∠4和∠5 内错角 AC DE BE AC BC BE ∠7和∠8 ∠2=∠6,∠5=∠7
【解析】由图可得,∠1,∠3与∠2互为同旁内角;
∠4,∠5与∠3互为同位角;
∠6与∠9是内错角,它们是直线AC与DE被直线BE所截得的;
∠3与∠5是直线AC与直线BC被直线BE所截得的同位角;
∠7,∠8与∠1是同位角;
根据对顶角相等可得,在标有数字的九个角中,大小一定相等的角有∠2=∠6,∠5=∠7.
故答案为:∠1,∠3;∠4,∠5;内错角,AC,DE,BE;AC,BC,BE;∠7,∠8;∠2=∠6,∠5=∠7.
11.【答案】对顶角相等
【解析】由题意得,扇形零件的圆心角与其两边的反向延长线组成的角是对顶角.因为对顶角相等,所以利用图中的量角器可以量出这个扇形零件的圆心角的度数.
故答案为对顶角相等.
12.【答案】平行
【解析】因为∠2=(220-3x)°,所以∠3=180°-∠2=(3x-40)°,
可得:∠1=∠3,所以AB与CD平行,故答案为平行.
13.【答案】30°
【解析】∵AD∥BC,∠CFE=50°,
∴∠AEF=∠CFE=50°,∠DEF=130°,
∴b图中的∠GEF=50°,∠DEG=180°-2×50°=80°,
∴c图中∠GFE=50°,
∴c图中∠DEF=80°-50°=30°.
故答案为30°.
14.【答案】50° 是
【解析】已知直线AB与CD相交于点O,且∠DOB=∠ODB,
若∠ODB=50°,则∠AOC=∠BOD=50°;∠CAO是∠AOC的同旁内角,
故答案为50°,是.
15.【答案】②③④
【解析】①根据内错角相等,两直线平行即可证得BD∥AC,不能证明AB∥CD;
②根据内错角相等,两直线平行即可证得AB∥CD;
③根据同位角相等,两直线平行即可证得AB∥CD;
④根据同旁内角互补,两直线平行,即可证得AB∥CD.
故答案为②③④.
16.【答案】14°
【解析】由OE⊥OF,∠EOF=90°.
由角的和差,得∠BOE=180°-∠AOF-∠EOF=180°-48°-90°=42°.
由∠BOC=2∠COE,角的和差,得
∠BOE=∠EOC+∠BOC=∠EOC+2∠EOC=3∠EOC=42°.
解得∠EOC=14°,故答案为14°.
17.【答案】∠DCE=∠MDF(答案不唯一).
【解析】∵AB∥CD,∴∠B=∠DCE.
∵∠MDF=∠B,∴∠DCE=∠MDF.
故答案为∠DCE=∠MDF(答案不唯一).
18.【答案】10或28
【解析】①两三角形在点O的同侧时,如图1,设CD与OB相交于点E,
∵AB∥CD,∴∠CEO=∠B=40°,
∵∠C=60°,∠COD=90°,∴∠D=90°-60°=30°,
∴∠DOE=∠CEO-∠D=40°-30°=10°,
∴旋转角∠AOD=∠AOB+∠DOE=90°+10°=100°,
∵每秒旋转10°,∴时间为100°÷10°=10秒;
②两三角形在点O的异侧时,如图2,延长BO与CD相交于点E,
∵AB∥CD,∴∠CEO=∠B=40°,
∵∠C=60°,∠COD=90°,∴∠D=90°-60°=30°,
∴∠DOE=∠CEO-∠D=40°-30°=10°,∴旋转角为270°+10°=280°,
∵每秒旋转10°,∴时间为280°÷10°=28秒;
综上所述,在第10或28秒时,边CD恰好与边AB平行.
故答案为10或28.
19.【答案】证明 (1)过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D+∠DEF=180°,(两直线平行,同旁内角互补)
∵∠B+∠BED+∠D=360°,(已知)
∴∠B+∠BEF=∠B+∠BED+∠D-(∠D+∠DEF)=360°-180°=180°,
∴EF∥AB,(同旁内角互补,两直线平行)
∴AB∥CD;(平行于同一直线的两直线平行)
(2)过E点作EF∥CD,(过直线外一点有且只有一条直线与已知直线平行),
∵EF∥CD,
∴∠D=∠FED,(两直线平行,内错角相等)
∵∠BED=∠B+∠D,(已知)
∴∠B=∠BED-∠D=∠BED-∠FED=∠BEF,
∴AB∥EF,(内错角相等,两直线平行)
∴AB∥CD.(平行于同一直线的两直线平行)
【解析】(1)过E点作EF∥CD,首先根据平行线的性质可得∠D+∠DEF=180°,然后可得∠B+∠BEF=180°,进而可根据同旁内角互补,两直线平行可得AB∥CD;
(2)过E点作EF∥CD,根据平行线的性质可得∠D=∠FED,进而可得∠B=∠BEF,根据内错角相等,两直线平行可得AB∥EF,再根据平行于同一直线的两直线平行可得AB∥CD.
20.【答案】如图1,∵OC⊥OA,OD⊥OB,
∴∠AOB+∠BOC=90°,∠COD+∠BOC=90°,∴∠COD=∠AOB=40°;
如图2,∵OC⊥OA,OD⊥OB,
∴∠AOC=∠BOD=90°,
∠BOC=∠AOC-∠AOB=90°-40°=50°,
∴∠COD=∠BOD+∠BOC=90°+50°=140°;
如图3,∠COD=360°-∠AOC-∠AOB-∠BOD=360°-90°-40°-90°=140°;
如图4,∵OC⊥OA,OD⊥OB,
∴∠AOB+∠AOD=90°,∠COD+∠AOD=90°,
∴∠COD=∠AOB=40°.
综上所述,∠COD的度数为40°或140°.
【解析】分OC、OD在边OA的同侧和异侧分别作出图形,然后分别进行计算即可得解.
21.【答案】∵∠FOC=90°,∠1=40°,AB为直线,
∴∠3+∠FOC+∠1=180°,∴∠3=180°-90°-40°=50°.
又∠3与∠AOD互补,∴∠AOD=180°-∠3=130°,
∵OE平分∠AOD,∴∠2=∠AOD=65°.
【解析】由已知∠FOC=90°,∠1=40°结合平角的定义,可得∠3的度数,又因为∠3与∠AOD互为补角,可求出∠AOD的度数,又由OE平分∠AOD可求出∠2.
22.【答案】∠ECB=90°.
理由:∵∠1=67°,∴∠2=67°.
∵∠3=23°,∴∠CBA=180°-67°-23°=90°.
∵CE∥AB,∴∠ECB=∠CBA=90°.
【解析】先根据平行线的性质求出∠2的度数,再由平角的定义求出∠CBA的度数,根据CE∥AB即可得出结论.
23.【答案】∵EF∥AD,∴∠1=∠3,
又∵∠1=∠2,∴∠2=∠3,∴AB∥DG,∴∠BAC+∠AGD=180°,
∵∠BAC=70°,∴∠AGD=110°.
【解析】由EF与AD平行,利用两直线平行同位角相等得到一对角相等,再由已知角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到DG与AB平行,利用两直线平行同旁内角互补,即可求出所求角的度数.
24.【答案】(1)如图①,过点E作EF∥AB,
∵AB∥CD,∴AB∥EF∥CD,∴∠ABE=∠BEF,∠FEC+∠ECD=180°,
∵∠ABE=30°,∠BEC=148°,∴∠FEC=118°,
∴∠ECD=180°-118°=62°;
(2)如图②,延长BE和DC相交于点G,
∵AB∥CD,∴∠ABE=∠G,∵BE∥CF,∴∠GEC=∠ECF,
∵∠ECD=∠GEC+∠G,∴∠ECD=∠ECF+∠ABE,
∵CF平分∠ECD,∴∠ECF=∠DCF,∴∠ECD=∠ECD+∠ABE,
∴∠ABE=∠ECD.
【解析】(1)过点E作EF∥AB,根据平行线的性质即可得到∠ECD的度数;
(2)延长BE和DC相交于点G,利用平行线的性质、三角形的外角以及角平分线的性质即可得到答案.
第二章
相交线与平行线
习题练习三(附答案)
一、选择题
1.如图所示,有下列五种说法:①∠1和∠4是同位角;②∠3和∠5是内错角;③∠2和∠6是同旁内角;④∠5和∠2是同位角;⑤∠1和∠3是同旁内角;其中正确的是( )
A.
①②③
B.
①②③④
C.
①②③④⑤
D.
①②④⑤
2.下列哪种方法不能检验直线与水平面是否垂直( )
A.
铅垂线
B.
两块三角尺
C.
长方形纸片
D.
合页型折纸
3.如图是五条胡同的路线图(A→B→C→D→E→F),经过测量得到∠B=∠C=70°,∠D=∠E=110°,则图中互相平行的线有( )
A.
1对B.
2对C.
3对D.
4对
4.小明在生日宴会上,要把一个大蛋糕分成七块,问他最少要切几次(切割成的蛋糕面积不一定相等)( )
A.
3次B.
4次C.
5次D.
6次
5.某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.
第一次左拐30°,第二次右拐30°
B.
第一次右拐50°,第二次左拐130°
C.
第一次右拐50°,第二次右拐130°
D.
第一次向左拐50°,第二次向左拐120°
6.如图,AB∥CD,则下列等式成立的是( )
A.
∠B+∠F+∠D=∠E+∠G
B.
∠E+∠F+∠G=∠B+∠D
C.
∠F+∠G+∠D=∠B+∠E
D.
∠B+∠E+∠F=∠G+∠D
7.如图,AB∥EF∥CD,∠ABC=44°,∠CEF=154°,则∠BCE等于( )
A.
22°
B.
18°
C.
20°
D.
26°
8.工人师傅对如图所示的零件进行加工,把材料弯成了一个40°的锐角,然后准备在A处第二次加工拐弯,要保证弯过来的部分与BC保持平行,弯的角度是( )
A.
40°
B.
140°
C.
40°或140°
D.
50°
9.同学们,你一定练过跳远吧!在测量跳远成绩时,从落地点拉向起跳线的皮尺,应当与起跳线( )
A.
平行B.
垂直C.
成45°D.
以上都不对
二、填空题
10.如图,与∠2互为同旁内角的是________;与∠3互为同位角的是________;∠6与∠9是______,它们是直线________与______被直线______所截得的;∠3与∠5是直线______与直线______被直线______所截得的;与∠1是同位角的有______,在标有数字的九个角中,大小一定相等的角有__________________.
11.如图所示,一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数,测量的根据是____________.
12.如图∠1=(3x-40)°,∠2=(220-3x)°,那么AB与CD的位置关系是________.
13.如图a是长方形纸带,∠CFE=50°,将纸带沿EF折叠成图b,再沿GE折叠成图c,则图c中∠DEF的度数是__________.
14.如图,已知直线AB与CD相交于点O,且∠DOB=∠ODB,若∠ODB=50°,则∠AOC的度数为______;∠CAO______(填“是”或“不是”)∠AOC的同旁内角.
15.如图,点E在AC的延长线上,对于下列给出的四个条件:
①∠3=∠4;②∠1=∠2;③∠A=∠DCE;④∠D+∠ABD=180°.
能判断AB∥CD的有_______________.(填正确结论的序号)
16.如图,点O为直线AB上的一点,OE,OF,OC是射线,OE⊥OF.若∠BOC=2∠COE,∠AOF=48°,求∠EOC的度数为_________.
17.如图,已知∠MDF=∠B,要得到AB∥CD,则需要添加的条件是:____________.
18.如图,Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,在旋转的过程中,在第________秒时,边CD恰好与边AB平行.
三、解答题
19.(1)如图1,已知∠B+∠BED+∠D=360°,求证AB∥CD.
(2)如图2,已知∠BED=∠B+∠D,求证AB∥CD.
20.如图,已知∠AOB=40°,画射线OC⊥OA,射线OD⊥OB,画出所有可能的情形并分别求出∠COD的度数.
21.如图所示,直线AB、CD相交于O,OE平分∠AOD,∠FOC=90°,∠1=40°,求∠2和∠3的度数.
22.如图,某工程队从A点出发,沿北偏西67度方向修一条公路AD,在BD路段出现塌陷区,就改变方向,由B点沿北偏东23度的方向继续修建BC段,到达C点又改变方向,使所修路段CE∥AB,此时∠ECB有多少度?试说明理由.
23.如图EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
24.已知AB∥CD.
(1)如图①,若∠ABE=30°,∠BEC=148°,求∠ECD的度数;
(2)如图②,若CF∥EB,CF平分∠ECD,试探究∠ECD与∠ABE之间的数量关系,并证明.
答案解析
1.【答案】D
【解析】根据内错角、同位角以及同旁内角的定义分析五种说法.
①∠1和∠4是同位角,即①成立;
②∠3和∠5是内错角,即②成立;
③∠2和∠6是内错角,即③不成立;
④∠5和∠2是同位角,即④成立;
⑤∠1和∠3是同旁内角,即⑤成立.
故选D.
2.【答案】C
【解析】A.根据重力学原理,铅垂线垂直于水平面;
B.将两块三角板的直角边重合,另外两条直角边相交,放在水平面上,可判断重合的直角边垂直于水平面;
C.长方形纸片只能判断长与宽互相垂直,不能判断与水平面垂直;
D.合页型折纸其折痕与纸被折断的一边垂直,即折痕与被折断的两线段垂直,把两放到水平面上,可判断折痕与水平面垂直;故选C.
3.【答案】D
【解析】∵∠B=∠C=70°,∴AB∥CD.
∵∠D=∠E=110°,∴CD∥EF,∴AB∥EF.
∵∠C+∠D=70°+110°=180°,∴BC∥DE.故选D.
4.【答案】A
【解析】设切n次,则+1≥7,解得n≥3或n≤-4(舍去),∴n≥3,故选A.
5.【答案】A
【解析】如图所示(实线为行驶路线):
A符合“同位角相等,两直线平行”的判定,其余均不符合平行线的判定.故选A.
6.【答案】A
【解析】过E作EM∥AB,过F作FH∥AB,过G作GN∥AB,
∵AB∥CD,∴AB∥EM∥GN∥CD∥FH,
∴∠B=∠BEM,∠FEM=∠HFE,∠HFG=∠FGN,∠D=∠NGD,
∴∠B+∠EFH+∠HFG+∠D=∠BEM+∠MEF+∠FGN+∠NGD,
∴∠B+∠EFG+∠D=∠BEF+∠FGD,故选A.
7.【答案】B
【解析】∵AB∥EF∥CD,∠ABC=44°,∠CEF=154°,
∴∠BCD=∠ABC=44°,∠FEC+∠ECD=180°,∴∠ECD=180°-∠FEC=26°,
∴∠BCE=∠BCD-∠ECD=44°-26°=18°.故选B.
8.【答案】C
【解析】如图1,作AE∥BC,则∠CBA=∠EAB=40°;
如图2,作AE∥BC,则∠CBA+∠EAB=180°,
∵∠CBA=40°,∴∠EAB=140°,
综上所述,弯的角度是40°或140°.故选C.
9.【答案】B
【解析】∵点到直线的垂线段的长叫点到直线的距离,
∴在测量跳远成绩时,从落地点拉向起跳线的皮尺,应当与起跳线垂直.故选B.
10.【答案】∠1和∠3 ∠4和∠5 内错角 AC DE BE AC BC BE ∠7和∠8 ∠2=∠6,∠5=∠7
【解析】由图可得,∠1,∠3与∠2互为同旁内角;
∠4,∠5与∠3互为同位角;
∠6与∠9是内错角,它们是直线AC与DE被直线BE所截得的;
∠3与∠5是直线AC与直线BC被直线BE所截得的同位角;
∠7,∠8与∠1是同位角;
根据对顶角相等可得,在标有数字的九个角中,大小一定相等的角有∠2=∠6,∠5=∠7.
故答案为:∠1,∠3;∠4,∠5;内错角,AC,DE,BE;AC,BC,BE;∠7,∠8;∠2=∠6,∠5=∠7.
11.【答案】对顶角相等
【解析】由题意得,扇形零件的圆心角与其两边的反向延长线组成的角是对顶角.因为对顶角相等,所以利用图中的量角器可以量出这个扇形零件的圆心角的度数.
故答案为对顶角相等.
12.【答案】平行
【解析】因为∠2=(220-3x)°,所以∠3=180°-∠2=(3x-40)°,
可得:∠1=∠3,所以AB与CD平行,故答案为平行.
13.【答案】30°
【解析】∵AD∥BC,∠CFE=50°,
∴∠AEF=∠CFE=50°,∠DEF=130°,
∴b图中的∠GEF=50°,∠DEG=180°-2×50°=80°,
∴c图中∠GFE=50°,
∴c图中∠DEF=80°-50°=30°.
故答案为30°.
14.【答案】50° 是
【解析】已知直线AB与CD相交于点O,且∠DOB=∠ODB,
若∠ODB=50°,则∠AOC=∠BOD=50°;∠CAO是∠AOC的同旁内角,
故答案为50°,是.
15.【答案】②③④
【解析】①根据内错角相等,两直线平行即可证得BD∥AC,不能证明AB∥CD;
②根据内错角相等,两直线平行即可证得AB∥CD;
③根据同位角相等,两直线平行即可证得AB∥CD;
④根据同旁内角互补,两直线平行,即可证得AB∥CD.
故答案为②③④.
16.【答案】14°
【解析】由OE⊥OF,∠EOF=90°.
由角的和差,得∠BOE=180°-∠AOF-∠EOF=180°-48°-90°=42°.
由∠BOC=2∠COE,角的和差,得
∠BOE=∠EOC+∠BOC=∠EOC+2∠EOC=3∠EOC=42°.
解得∠EOC=14°,故答案为14°.
17.【答案】∠DCE=∠MDF(答案不唯一).
【解析】∵AB∥CD,∴∠B=∠DCE.
∵∠MDF=∠B,∴∠DCE=∠MDF.
故答案为∠DCE=∠MDF(答案不唯一).
18.【答案】10或28
【解析】①两三角形在点O的同侧时,如图1,设CD与OB相交于点E,
∵AB∥CD,∴∠CEO=∠B=40°,
∵∠C=60°,∠COD=90°,∴∠D=90°-60°=30°,
∴∠DOE=∠CEO-∠D=40°-30°=10°,
∴旋转角∠AOD=∠AOB+∠DOE=90°+10°=100°,
∵每秒旋转10°,∴时间为100°÷10°=10秒;
②两三角形在点O的异侧时,如图2,延长BO与CD相交于点E,
∵AB∥CD,∴∠CEO=∠B=40°,
∵∠C=60°,∠COD=90°,∴∠D=90°-60°=30°,
∴∠DOE=∠CEO-∠D=40°-30°=10°,∴旋转角为270°+10°=280°,
∵每秒旋转10°,∴时间为280°÷10°=28秒;
综上所述,在第10或28秒时,边CD恰好与边AB平行.
故答案为10或28.
19.【答案】证明 (1)过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D+∠DEF=180°,(两直线平行,同旁内角互补)
∵∠B+∠BED+∠D=360°,(已知)
∴∠B+∠BEF=∠B+∠BED+∠D-(∠D+∠DEF)=360°-180°=180°,
∴EF∥AB,(同旁内角互补,两直线平行)
∴AB∥CD;(平行于同一直线的两直线平行)
(2)过E点作EF∥CD,(过直线外一点有且只有一条直线与已知直线平行),
∵EF∥CD,
∴∠D=∠FED,(两直线平行,内错角相等)
∵∠BED=∠B+∠D,(已知)
∴∠B=∠BED-∠D=∠BED-∠FED=∠BEF,
∴AB∥EF,(内错角相等,两直线平行)
∴AB∥CD.(平行于同一直线的两直线平行)
【解析】(1)过E点作EF∥CD,首先根据平行线的性质可得∠D+∠DEF=180°,然后可得∠B+∠BEF=180°,进而可根据同旁内角互补,两直线平行可得AB∥CD;
(2)过E点作EF∥CD,根据平行线的性质可得∠D=∠FED,进而可得∠B=∠BEF,根据内错角相等,两直线平行可得AB∥EF,再根据平行于同一直线的两直线平行可得AB∥CD.
20.【答案】如图1,∵OC⊥OA,OD⊥OB,
∴∠AOB+∠BOC=90°,∠COD+∠BOC=90°,∴∠COD=∠AOB=40°;
如图2,∵OC⊥OA,OD⊥OB,
∴∠AOC=∠BOD=90°,
∠BOC=∠AOC-∠AOB=90°-40°=50°,
∴∠COD=∠BOD+∠BOC=90°+50°=140°;
如图3,∠COD=360°-∠AOC-∠AOB-∠BOD=360°-90°-40°-90°=140°;
如图4,∵OC⊥OA,OD⊥OB,
∴∠AOB+∠AOD=90°,∠COD+∠AOD=90°,
∴∠COD=∠AOB=40°.
综上所述,∠COD的度数为40°或140°.
【解析】分OC、OD在边OA的同侧和异侧分别作出图形,然后分别进行计算即可得解.
21.【答案】∵∠FOC=90°,∠1=40°,AB为直线,
∴∠3+∠FOC+∠1=180°,∴∠3=180°-90°-40°=50°.
又∠3与∠AOD互补,∴∠AOD=180°-∠3=130°,
∵OE平分∠AOD,∴∠2=∠AOD=65°.
【解析】由已知∠FOC=90°,∠1=40°结合平角的定义,可得∠3的度数,又因为∠3与∠AOD互为补角,可求出∠AOD的度数,又由OE平分∠AOD可求出∠2.
22.【答案】∠ECB=90°.
理由:∵∠1=67°,∴∠2=67°.
∵∠3=23°,∴∠CBA=180°-67°-23°=90°.
∵CE∥AB,∴∠ECB=∠CBA=90°.
【解析】先根据平行线的性质求出∠2的度数,再由平角的定义求出∠CBA的度数,根据CE∥AB即可得出结论.
23.【答案】∵EF∥AD,∴∠1=∠3,
又∵∠1=∠2,∴∠2=∠3,∴AB∥DG,∴∠BAC+∠AGD=180°,
∵∠BAC=70°,∴∠AGD=110°.
【解析】由EF与AD平行,利用两直线平行同位角相等得到一对角相等,再由已知角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到DG与AB平行,利用两直线平行同旁内角互补,即可求出所求角的度数.
24.【答案】(1)如图①,过点E作EF∥AB,
∵AB∥CD,∴AB∥EF∥CD,∴∠ABE=∠BEF,∠FEC+∠ECD=180°,
∵∠ABE=30°,∠BEC=148°,∴∠FEC=118°,
∴∠ECD=180°-118°=62°;
(2)如图②,延长BE和DC相交于点G,
∵AB∥CD,∴∠ABE=∠G,∵BE∥CF,∴∠GEC=∠ECF,
∵∠ECD=∠GEC+∠G,∴∠ECD=∠ECF+∠ABE,
∵CF平分∠ECD,∴∠ECF=∠DCF,∴∠ECD=∠ECD+∠ABE,
∴∠ABE=∠ECD.
【解析】(1)过点E作EF∥AB,根据平行线的性质即可得到∠ECD的度数;
(2)延长BE和DC相交于点G,利用平行线的性质、三角形的外角以及角平分线的性质即可得到答案.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
