9.2 多边形的内角和与外角和 同步练习(含解析)
文档属性
| 名称 | 9.2 多边形的内角和与外角和 同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 267.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-02 00:00:00 | ||
图片预览

文档简介
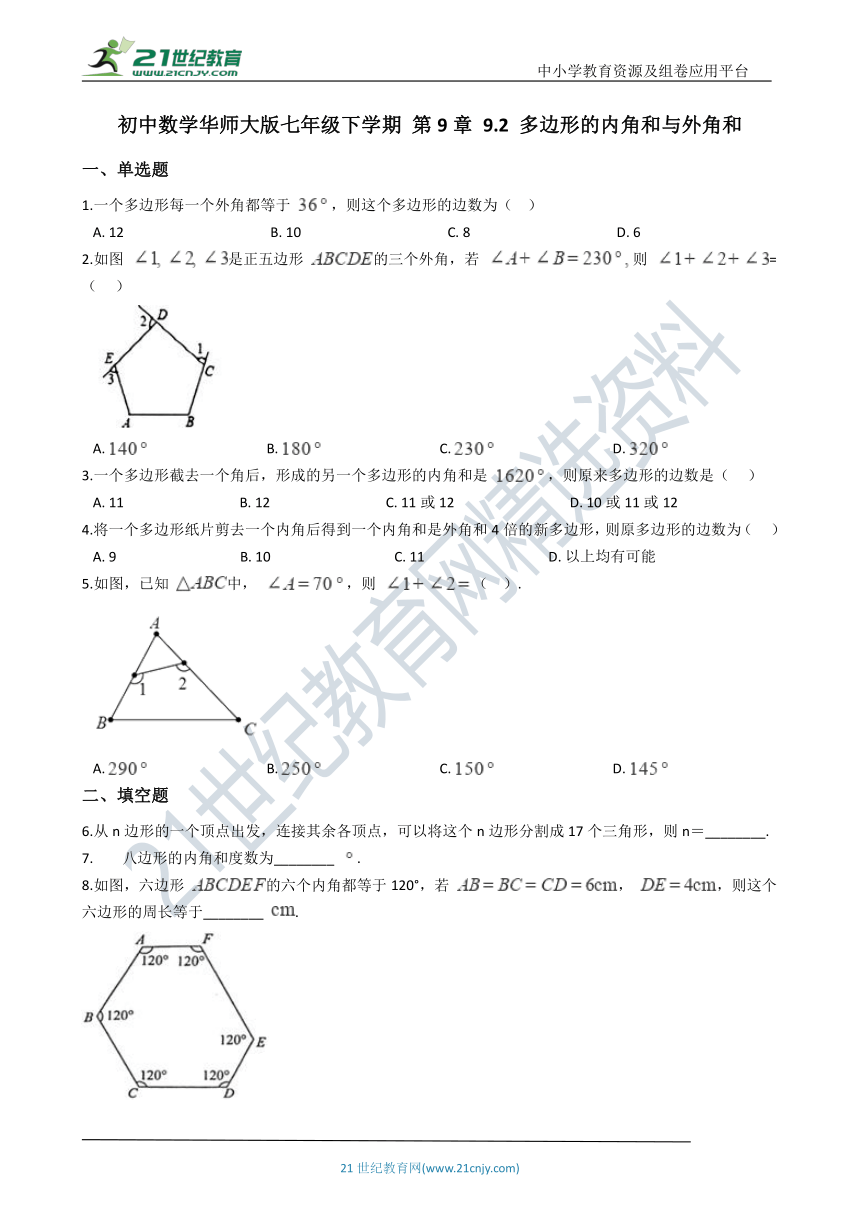
初中数学华师大版七年级下学期 第9章 9.2 多边形的内角和与外角和
一、单选题
1.一个多边形每一个外角都等于 ,则这个多边形的边数为(?? )
A.?12??????????????????????????????????????????B.?10??????????????????????????????????????????C.?8??????????????????????????????????????????D.?6
2.如图 是正五边形 的三个外角,若 则 =(??? )
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
3.一个多边形截去一个角后,形成的另一个多边形的内角和是 ,则原来多边形的边数是(??? )
A.?11?????????????????????????????????B.?12?????????????????????????????????C.?11或12?????????????????????????????????D.?10或11或12
4.将一个多边形纸片剪去一个内角后得到一个内角和是外角和4倍的新多边形,则原多边形的边数为(??? )
A.?9????????????????????????????????????B.?10????????????????????????????????????C.?11????????????????????????????????????D.?以上均有可能
5.如图,已知 中, ,则 (?? ).
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
二、填空题
6.从n边形的一个顶点出发,连接其余各顶点,可以将这个n边形分割成17个三角形,则n=________.
7.???? 八边形的内角和度数为________ .
8.如图,六边形 的六个内角都等于120°,若 , ,则这个六边形的周长等于________ .
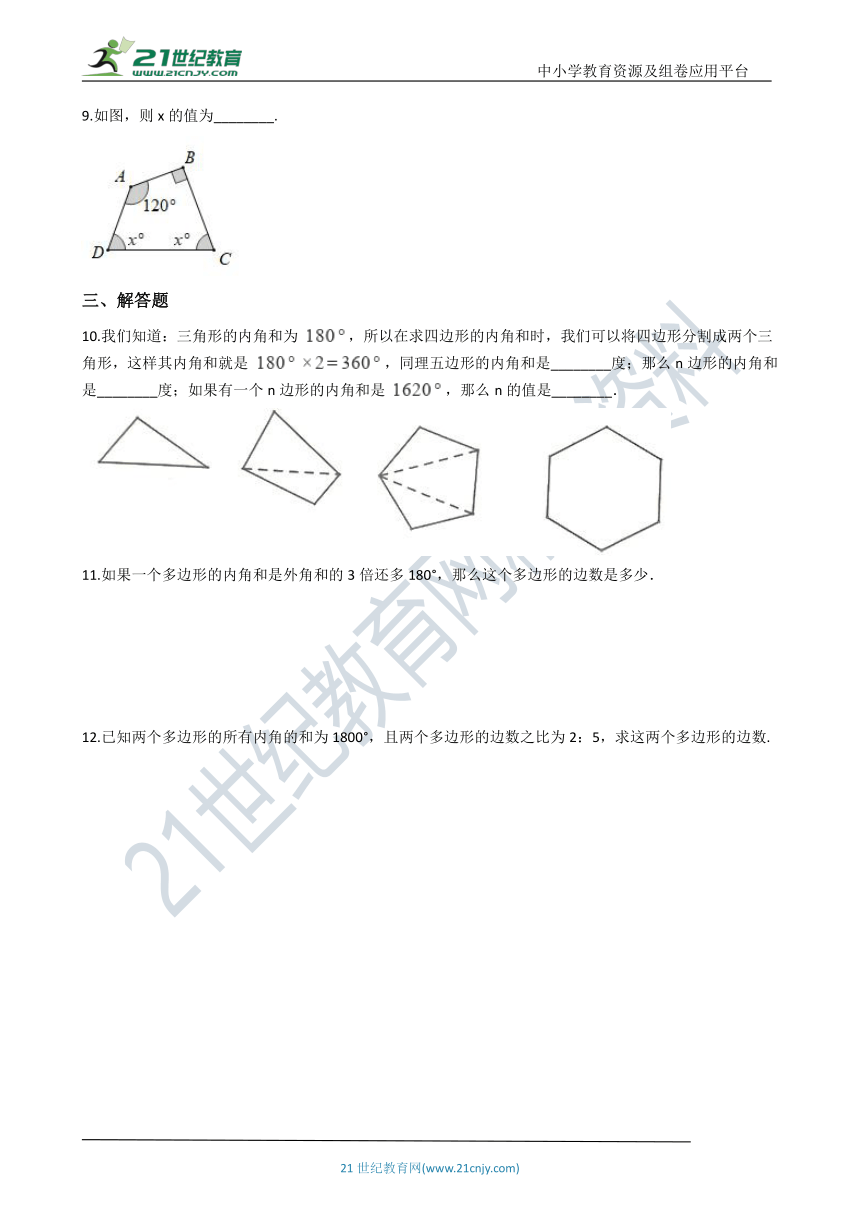
9.如图,则x的值为________.
三、解答题
10.我们知道:三角形的内角和为 ,所以在求四边形的内角和时,我们可以将四边形分割成两个三角形,这样其内角和就是 ,同理五边形的内角和是________度;那么n边形的内角和是________度;如果有一个n边形的内角和是 ,那么n的值是________.
11.如果一个多边形的内角和是外角和的3倍还多180°,那么这个多边形的边数是多少.
12.已知两个多边形的所有内角的和为1800°,且两个多边形的边数之比为2:5,求这两个多边形的边数.
答案解析部分
一、单选题
1.【答案】 B
解: ,
则这个多边形的边数为10,
故答案为:B .
2.【答案】 C
解:根据题意,五边形的内角和为: ,
∵
,
∵ ,
∴ ;
故答案为:C.
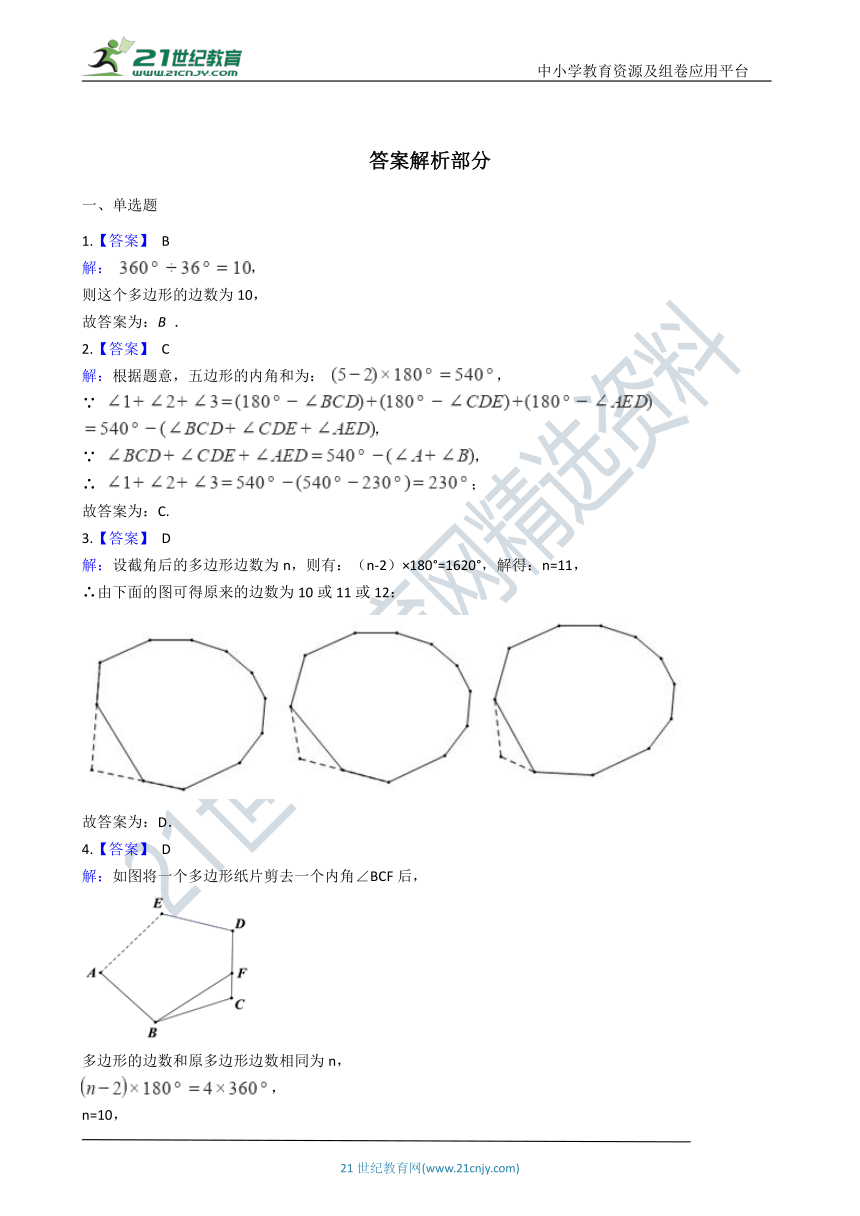
3.【答案】 D
解:设截角后的多边形边数为n,则有:(n-2)×180°=1620°,解得:n=11,
∴由下面的图可得原来的边数为10或11或12:
故答案为:D.
4.【答案】 D
解:如图将一个多边形纸片剪去一个内角∠BCF后,
多边形的边数和原多边形边数相同为n,
,
n=10,
如图将一个多边形纸片剪去一个内角∠BCF后,
多边形的边数比原多边形边数少1为n-1,
,
n=11,
如图将一个多边形纸片剪去一个内角∠GCF后,
多边形的边数比原多边形边数多1为n+1,
,
n=9,
原多边形的边数为9,10,11.
故答案为:D.
5.【答案】 B
解:∵∠A+∠B+∠C=180°,
而∠A=70°
∴∠B+∠C=110°,
∵∠1+∠2+∠B+∠C=360°,
∴∠1+∠2=250°.
故答案为:B.
二、填空题
6.【答案】 19
解:∵一个多边形从一个顶点出发,连接其余各顶点,可以把多边形分成(n-2)个三角形,
∴n-2=17,
∴ .
故答案为:19.
7.【答案】 1080
解:八边形的内角和为: .
故答案为:1080.
8.【答案】 34
解:如图,分别作AB、CD、EF的延长线和反向延长线,使它们交于点G、H、P,
∵六边形ABCDEF的六个角都是120°,
∴六边形ABCDEF的每一个外角的度数都是60°,
∴△APF、△BGC、△DHE、△GHP都是等边三角形,
∴GC=BC=6cm,DH=DE=4cm,PF=PA=FA,
∴GH=6+6+4=16cm,
∴FA=PA=PG-AB-BG=16-6-6=4cm,EF=PH-PF-EH=16-4-4=8cm,
∴六边形的周长为6+6+6+4+8+4=34cm.
故答案为:34.
9.【答案】 75
解:四边形的内角和为(4-2) 180° =360°,故
,
解得: ,
故答案为:75.
三、解答题
10.【答案】 540;(n-2)×180;11
解:五边形可以分成三个三角形,内角和是:180°×3=540°,
一个n边形可分成n-2个三角形,内角和是:(n-2)×180°;
根据n边形的内角和是 可得,
,
解得 n=11 ,
故答案为:540,(n-2)×180,11.
11.【答案】 解:设这个多边形的边数为n,
根据题意,得(n?2)·180=360×3+180,
解得:n=9.
则这个多边形的边数是9.
12.【答案】 解:设一个多边形的边数为2x,另一个多边形的边数为5x,
根据题意可得(2x﹣2)·180°+(5x﹣2)·180°=1800°,
解得x=2,
故这两个多边形的边数分别是4和10.
一、单选题
1.一个多边形每一个外角都等于 ,则这个多边形的边数为(?? )
A.?12??????????????????????????????????????????B.?10??????????????????????????????????????????C.?8??????????????????????????????????????????D.?6
2.如图 是正五边形 的三个外角,若 则 =(??? )
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
3.一个多边形截去一个角后,形成的另一个多边形的内角和是 ,则原来多边形的边数是(??? )
A.?11?????????????????????????????????B.?12?????????????????????????????????C.?11或12?????????????????????????????????D.?10或11或12
4.将一个多边形纸片剪去一个内角后得到一个内角和是外角和4倍的新多边形,则原多边形的边数为(??? )
A.?9????????????????????????????????????B.?10????????????????????????????????????C.?11????????????????????????????????????D.?以上均有可能
5.如图,已知 中, ,则 (?? ).
A.??????????????????????????????????B.??????????????????????????????????C.??????????????????????????????????D.?
二、填空题
6.从n边形的一个顶点出发,连接其余各顶点,可以将这个n边形分割成17个三角形,则n=________.
7.???? 八边形的内角和度数为________ .
8.如图,六边形 的六个内角都等于120°,若 , ,则这个六边形的周长等于________ .
9.如图,则x的值为________.
三、解答题
10.我们知道:三角形的内角和为 ,所以在求四边形的内角和时,我们可以将四边形分割成两个三角形,这样其内角和就是 ,同理五边形的内角和是________度;那么n边形的内角和是________度;如果有一个n边形的内角和是 ,那么n的值是________.
11.如果一个多边形的内角和是外角和的3倍还多180°,那么这个多边形的边数是多少.
12.已知两个多边形的所有内角的和为1800°,且两个多边形的边数之比为2:5,求这两个多边形的边数.
答案解析部分
一、单选题
1.【答案】 B
解: ,
则这个多边形的边数为10,
故答案为:B .
2.【答案】 C
解:根据题意,五边形的内角和为: ,
∵
,
∵ ,
∴ ;
故答案为:C.
3.【答案】 D
解:设截角后的多边形边数为n,则有:(n-2)×180°=1620°,解得:n=11,
∴由下面的图可得原来的边数为10或11或12:
故答案为:D.
4.【答案】 D
解:如图将一个多边形纸片剪去一个内角∠BCF后,
多边形的边数和原多边形边数相同为n,
,
n=10,
如图将一个多边形纸片剪去一个内角∠BCF后,
多边形的边数比原多边形边数少1为n-1,
,
n=11,
如图将一个多边形纸片剪去一个内角∠GCF后,
多边形的边数比原多边形边数多1为n+1,
,
n=9,
原多边形的边数为9,10,11.
故答案为:D.
5.【答案】 B
解:∵∠A+∠B+∠C=180°,
而∠A=70°
∴∠B+∠C=110°,
∵∠1+∠2+∠B+∠C=360°,
∴∠1+∠2=250°.
故答案为:B.
二、填空题
6.【答案】 19
解:∵一个多边形从一个顶点出发,连接其余各顶点,可以把多边形分成(n-2)个三角形,
∴n-2=17,
∴ .
故答案为:19.
7.【答案】 1080
解:八边形的内角和为: .
故答案为:1080.
8.【答案】 34
解:如图,分别作AB、CD、EF的延长线和反向延长线,使它们交于点G、H、P,
∵六边形ABCDEF的六个角都是120°,
∴六边形ABCDEF的每一个外角的度数都是60°,
∴△APF、△BGC、△DHE、△GHP都是等边三角形,
∴GC=BC=6cm,DH=DE=4cm,PF=PA=FA,
∴GH=6+6+4=16cm,
∴FA=PA=PG-AB-BG=16-6-6=4cm,EF=PH-PF-EH=16-4-4=8cm,
∴六边形的周长为6+6+6+4+8+4=34cm.
故答案为:34.
9.【答案】 75
解:四边形的内角和为(4-2) 180° =360°,故
,
解得: ,
故答案为:75.
三、解答题
10.【答案】 540;(n-2)×180;11
解:五边形可以分成三个三角形,内角和是:180°×3=540°,
一个n边形可分成n-2个三角形,内角和是:(n-2)×180°;
根据n边形的内角和是 可得,
,
解得 n=11 ,
故答案为:540,(n-2)×180,11.
11.【答案】 解:设这个多边形的边数为n,
根据题意,得(n?2)·180=360×3+180,
解得:n=9.
则这个多边形的边数是9.
12.【答案】 解:设一个多边形的边数为2x,另一个多边形的边数为5x,
根据题意可得(2x﹣2)·180°+(5x﹣2)·180°=1800°,
解得x=2,
故这两个多边形的边数分别是4和10.
