9.3 用正多边形铺设地面 同步练习(含解析)
文档属性
| 名称 | 9.3 用正多边形铺设地面 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 199.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-02 08:38:56 | ||
图片预览

文档简介
初中数学华师大版七年级下学期 第9章 9.3 用正多边形铺设地面
一、单选题
1.分别剪一些边长相同的①正三角形,②正方形,③正五边形,④正六边形,如果用其中一种正多边形镶嵌,可以镶嵌成一个平面图案的有( ???)
A.?①②③???????????????????????????B.?②③④???????????????????????????C.?①②④???????????????????????????D.?①②③④都可以
2.某市对人行道路翻新,准备选用—种正多边形铺设地面,下列地砖中,不能在平面镶嵌中铺满地面的是(? )
A.?正三角形?????????????????????????????B.?正方形?????????????????????????????C.?正五边形?????????????????????????????D.?正六边形
3.用三种边长相等的正多边形地砖铺地,其顶点拼在一起,刚好能完全铺满地面.已知正多边形的边数为x,y,z,则 的值为(? ?)
A.?1??????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
4.如图所示,一个正方形水池的四周恰好被4个正n边形地板砖铺满,则 等于(?? )
A.?6???????????????????????????????????????????B.?8???????????????????????????????????????????C.?9???????????????????????????????????????????D.?10
5.商店出售下列形状的地砖:
①长方形;②正方形;③正五边形;④正六边形.
若只选购其中某一种地砖镶嵌地面,可供选择的地砖共有( )
A.?1种???????????????????????????????????????B.?2种???????????????????????????????????????C.?3种???????????????????????????????????????D.?4种
6.在现实生活中,铺地最常见的是用正方形地板砖,某小区广场准备用多种地板砖组合铺设,则能够选择的组合是
A.?正三角形,正方形??????B.?正方形,正六边形??????C.?正五边形,正六边形??????D.?正六边形,正八边形
7.将若干个大小相等的正五边形排成环状,如图所示是前3个五边形,要完成这一圆环还需(??? )个正五边形
A.?6???????????????????????????????????????????B.?7???????????????????????????????????????????C.?8???????????????????????????????????????????D.?9
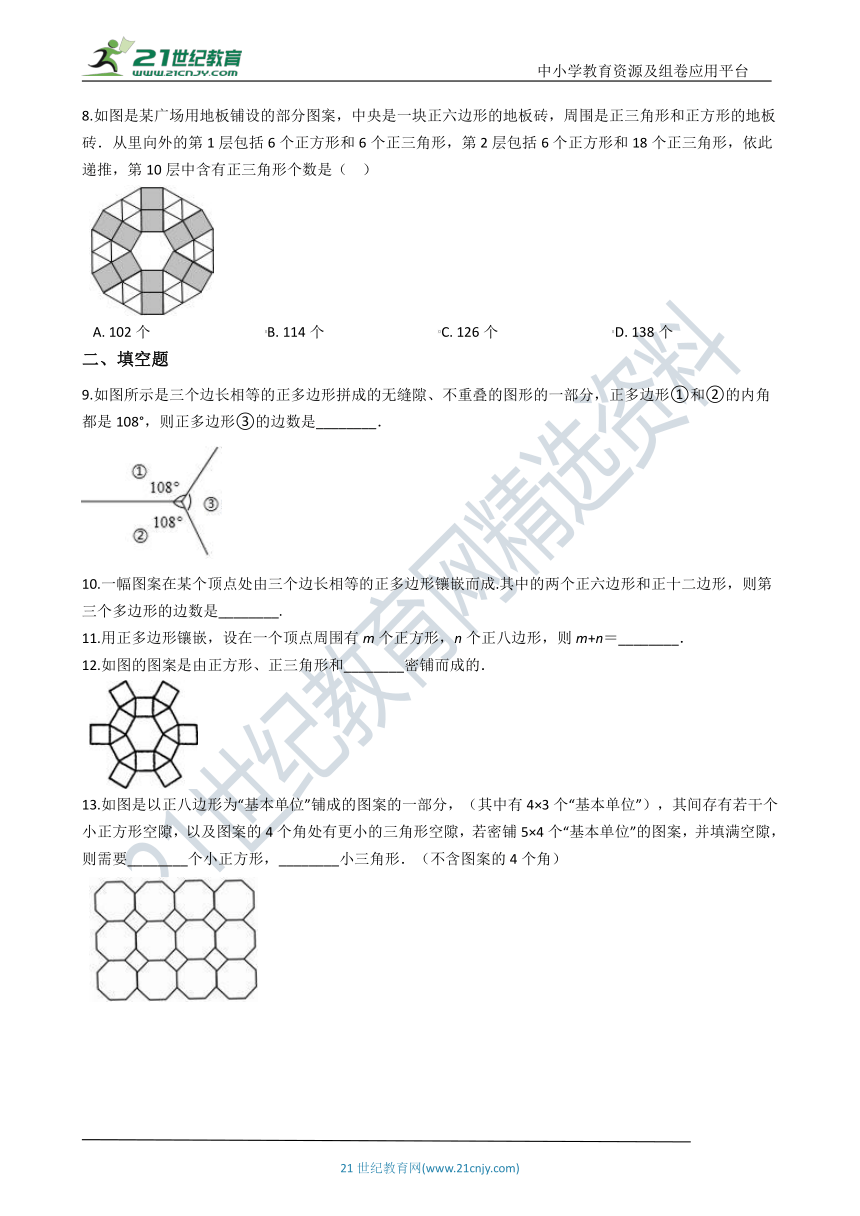
8.如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6个正三角形,第2层包括6个正方形和18个正三角形,依此递推,第10层中含有正三角形个数是(?? )
A.?102个?????????????????????????????????B.?114个?????????????????????????????????C.?126个?????????????????????????????????D.?138个
二、填空题
9.如图所示是三个边长相等的正多边形拼成的无缝隙、不重叠的图形的一部分,正多边形①和②的内角都是108°,则正多边形③的边数是________.
10.一幅图案在某个顶点处由三个边长相等的正多边形镶嵌而成.其中的两个正六边形和正十二边形,则第三个多边形的边数是________.
11.用正多边形镶嵌,设在一个顶点周围有m个正方形,n个正八边形,则m+n=________.
12.如图的图案是由正方形、正三角形和________密铺而成的.
13.如图是以正八边形为“基本单位”铺成的图案的一部分,(其中有4×3个“基本单位”),其间存有若干个小正方形空隙,以及图案的4个角处有更小的三角形空隙,若密铺5×4个“基本单位”的图案,并填满空隙,则需要________个小正方形,________小三角形.(不含图案的4个角)
答案解析部分
一、单选题
1.【答案】 C
解:①、正三角形的每个内角是60°,能整除360°,能密铺;②、正方形的每个内角是90°,4个能密铺;③、正五边形每个内角是180°﹣360°÷5=108°,不能整除360°,不能密铺;④、正六边形的每个内角是120°,能整除360°,能密铺.
正确的为①②④.
故答案为:C.
2.【答案】 C
解:A、正三角形的每个内角是60°,能整除360°,能密铺;
B、正方形的每个内角是90°,4个能密铺;
C、正五边形每个内角是180°-360°÷5=108°,不能整除360°,不能密铺;
D、正六边形的每个内角是120°,能整除360°,3个能密铺.
故答案为:C.
3.【答案】 C
解:由题意知,这3种多边形的3个内角之和为360度,已知正多边形的边数为x、y、z,那么这三个多边形的内角和可表示为: + + =360,两边都除以180得:1﹣ +1﹣ +1﹣ =2,两边都除以2得: + + = .
故答案为:C.
4.【答案】 B
解:解:正n边形的一个内角=(360°-90°)÷2=135°,则135°n=(n-2)180°,
解得n=8,故本题选B.
5.【答案】 C
解:①长方形的每个内角是90°,4个能组成镶嵌;
②正方形的每个内角是90°,4个能组成镶嵌;
③正五边形每个内角是180°﹣360°÷5=108°,不能整除360°,不能镶嵌;
④正六边形的每个内角是120°,能整除360°,3个能组成镶嵌;
故若只选购其中某一种地砖镶嵌地面,可供选择的地砖有①②④.
故答案为:C.
6.【答案】 A
解:∵正三角形的每个内角60°,正方形的每个内角是90°,正五边形的每个内角是108°,正六边形的每个内角是120°,正八边形每个内角是180°-360°÷8=135°
又∵60°×3+90°×2=360°
∴能够组合是正三角形,正方形
7.【答案】 B
解:五边形的内角和为(5﹣2)?180°=540°,
所以正五边形的每一个内角为540°÷5=108°,
如图,延长正五边形的两边相交于点O , 则∠1=360°﹣108°×3=360°﹣324°=36°,
360°÷36°=10,
∵已经有3个五边形,
∴10﹣3=7,
即完成这一圆环还需7个五边形.
故答案为:B .
8.【答案】 B
解:根据题意分析可得:从里向外的第1层包括6个正三角形.
第2层包括18个正三角形.
此后,每层都比前一层多12个.
依此递推,第10层中含有正三角形个数是6+12×9=114个.
故答案为:B.
二、填空题
9.【答案】 10.
解:360°?108°?108°=144°,
180°?144°=36°,
360°÷36°=10.
故答案为10.
10.【答案】 4
解:由于正六边形和正十二边形内角分别为120°、150°,
∵360?(150+120)=90,
又∵正方形内角为90°,
∴第三个正多边形的边数是4.
故答案为:4.
11.【答案】 3
解:由题意,有135n+90m=360,
m=4﹣ ,
因为m、n为整数,
∴n=2,m=1,
m+n═3,
故答案为3.
12.【答案】 正六边形
解:围绕一点观察图形可知如图的图案是由正方形、正三角形和 正六边形密铺而成的.
故答案为:正六边形.
13.【答案】 12;14
解:小正方形4×3=12;小三角形的个数为4×2+3×2=14,
故答案为:12,14.
一、单选题
1.分别剪一些边长相同的①正三角形,②正方形,③正五边形,④正六边形,如果用其中一种正多边形镶嵌,可以镶嵌成一个平面图案的有( ???)
A.?①②③???????????????????????????B.?②③④???????????????????????????C.?①②④???????????????????????????D.?①②③④都可以
2.某市对人行道路翻新,准备选用—种正多边形铺设地面,下列地砖中,不能在平面镶嵌中铺满地面的是(? )
A.?正三角形?????????????????????????????B.?正方形?????????????????????????????C.?正五边形?????????????????????????????D.?正六边形
3.用三种边长相等的正多边形地砖铺地,其顶点拼在一起,刚好能完全铺满地面.已知正多边形的边数为x,y,z,则 的值为(? ?)
A.?1??????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
4.如图所示,一个正方形水池的四周恰好被4个正n边形地板砖铺满,则 等于(?? )
A.?6???????????????????????????????????????????B.?8???????????????????????????????????????????C.?9???????????????????????????????????????????D.?10
5.商店出售下列形状的地砖:
①长方形;②正方形;③正五边形;④正六边形.
若只选购其中某一种地砖镶嵌地面,可供选择的地砖共有( )
A.?1种???????????????????????????????????????B.?2种???????????????????????????????????????C.?3种???????????????????????????????????????D.?4种
6.在现实生活中,铺地最常见的是用正方形地板砖,某小区广场准备用多种地板砖组合铺设,则能够选择的组合是
A.?正三角形,正方形??????B.?正方形,正六边形??????C.?正五边形,正六边形??????D.?正六边形,正八边形
7.将若干个大小相等的正五边形排成环状,如图所示是前3个五边形,要完成这一圆环还需(??? )个正五边形
A.?6???????????????????????????????????????????B.?7???????????????????????????????????????????C.?8???????????????????????????????????????????D.?9
8.如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6个正三角形,第2层包括6个正方形和18个正三角形,依此递推,第10层中含有正三角形个数是(?? )
A.?102个?????????????????????????????????B.?114个?????????????????????????????????C.?126个?????????????????????????????????D.?138个
二、填空题
9.如图所示是三个边长相等的正多边形拼成的无缝隙、不重叠的图形的一部分,正多边形①和②的内角都是108°,则正多边形③的边数是________.
10.一幅图案在某个顶点处由三个边长相等的正多边形镶嵌而成.其中的两个正六边形和正十二边形,则第三个多边形的边数是________.
11.用正多边形镶嵌,设在一个顶点周围有m个正方形,n个正八边形,则m+n=________.
12.如图的图案是由正方形、正三角形和________密铺而成的.
13.如图是以正八边形为“基本单位”铺成的图案的一部分,(其中有4×3个“基本单位”),其间存有若干个小正方形空隙,以及图案的4个角处有更小的三角形空隙,若密铺5×4个“基本单位”的图案,并填满空隙,则需要________个小正方形,________小三角形.(不含图案的4个角)
答案解析部分
一、单选题
1.【答案】 C
解:①、正三角形的每个内角是60°,能整除360°,能密铺;②、正方形的每个内角是90°,4个能密铺;③、正五边形每个内角是180°﹣360°÷5=108°,不能整除360°,不能密铺;④、正六边形的每个内角是120°,能整除360°,能密铺.
正确的为①②④.
故答案为:C.
2.【答案】 C
解:A、正三角形的每个内角是60°,能整除360°,能密铺;
B、正方形的每个内角是90°,4个能密铺;
C、正五边形每个内角是180°-360°÷5=108°,不能整除360°,不能密铺;
D、正六边形的每个内角是120°,能整除360°,3个能密铺.
故答案为:C.
3.【答案】 C
解:由题意知,这3种多边形的3个内角之和为360度,已知正多边形的边数为x、y、z,那么这三个多边形的内角和可表示为: + + =360,两边都除以180得:1﹣ +1﹣ +1﹣ =2,两边都除以2得: + + = .
故答案为:C.
4.【答案】 B
解:解:正n边形的一个内角=(360°-90°)÷2=135°,则135°n=(n-2)180°,
解得n=8,故本题选B.
5.【答案】 C
解:①长方形的每个内角是90°,4个能组成镶嵌;
②正方形的每个内角是90°,4个能组成镶嵌;
③正五边形每个内角是180°﹣360°÷5=108°,不能整除360°,不能镶嵌;
④正六边形的每个内角是120°,能整除360°,3个能组成镶嵌;
故若只选购其中某一种地砖镶嵌地面,可供选择的地砖有①②④.
故答案为:C.
6.【答案】 A
解:∵正三角形的每个内角60°,正方形的每个内角是90°,正五边形的每个内角是108°,正六边形的每个内角是120°,正八边形每个内角是180°-360°÷8=135°
又∵60°×3+90°×2=360°
∴能够组合是正三角形,正方形
7.【答案】 B
解:五边形的内角和为(5﹣2)?180°=540°,
所以正五边形的每一个内角为540°÷5=108°,
如图,延长正五边形的两边相交于点O , 则∠1=360°﹣108°×3=360°﹣324°=36°,
360°÷36°=10,
∵已经有3个五边形,
∴10﹣3=7,
即完成这一圆环还需7个五边形.
故答案为:B .
8.【答案】 B
解:根据题意分析可得:从里向外的第1层包括6个正三角形.
第2层包括18个正三角形.
此后,每层都比前一层多12个.
依此递推,第10层中含有正三角形个数是6+12×9=114个.
故答案为:B.
二、填空题
9.【答案】 10.
解:360°?108°?108°=144°,
180°?144°=36°,
360°÷36°=10.
故答案为10.
10.【答案】 4
解:由于正六边形和正十二边形内角分别为120°、150°,
∵360?(150+120)=90,
又∵正方形内角为90°,
∴第三个正多边形的边数是4.
故答案为:4.
11.【答案】 3
解:由题意,有135n+90m=360,
m=4﹣ ,
因为m、n为整数,
∴n=2,m=1,
m+n═3,
故答案为3.
12.【答案】 正六边形
解:围绕一点观察图形可知如图的图案是由正方形、正三角形和 正六边形密铺而成的.
故答案为:正六边形.
13.【答案】 12;14
解:小正方形4×3=12;小三角形的个数为4×2+3×2=14,
故答案为:12,14.
