第9章 多边形 单元测试卷(含解析)
文档属性
| 名称 | 第9章 多边形 单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 548.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-02 08:46:22 | ||
图片预览

文档简介
初中数学华师大版七年级下学期
第9章测试卷
一、单选题
1.若一个三角形的两边长分别为4和8,则第三边长可以是(??????
)
A.?4?????????????????????????????????????????B.?12?????????????????????????????????????????C.?13?????????????????????????????????????????D.?10
2.如图所示,在△ABC中,D为AB上一点,E为BC上一点,且AC
=
CD
=
BD
=
BE,∠A
=
50°,则∠CDE的度数为(??
)
A.?50°?????????????????????????????????????B.?51°?????????????????????????????????????C.?51.5°?????????????????????????????????????D.?52.5°
3.如图,
是等边三角形,
是等腰直角三角形,
,连接BD,则
的度数为(??
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
4.如果在
中,
,则
等于(??
)
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
5.下列长度的三根小木棒能构成三角形的是(??
)
A.?1cm,2
cm,3
cm????????????????????????????????????????????B.?2
cm,4
cm,6
cm
C.?3
cm,4
cm,8
cm???????????????????????????????????????????D.?6
cm,8
cm,10
cm
6.已知一个等腰三角形两内角的度数之比为
,则这个等腰三角形顶角的度数为(??
)
A.???????????????????????????????????B.???????????????????????????????????C.?或
??????????????????????????????????D.?
7.用下列边长相同的正多边形组合,能够铺满地面不留缝隙的是(??
)
A.?正八边形和正三角形???????????????????????????????????????????B.?正五边形和正八边形
C.?正六边形和正三角形???????????????????????????????????????????D.?正六边形和正五边形
8.如图所示的图形中,能够用一个图形镶嵌整个平面的有(?
)个
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
二、填空题
9.已知△ABC的两条边长分别为2和5,则第三边c的取值范围是________.
10.如果小明沿着坡度为
的山坡向上走了130米,那么他的高度上升了________米.
11.一个多边形的每个外角都等于72°,则这个多边形的边数为________.
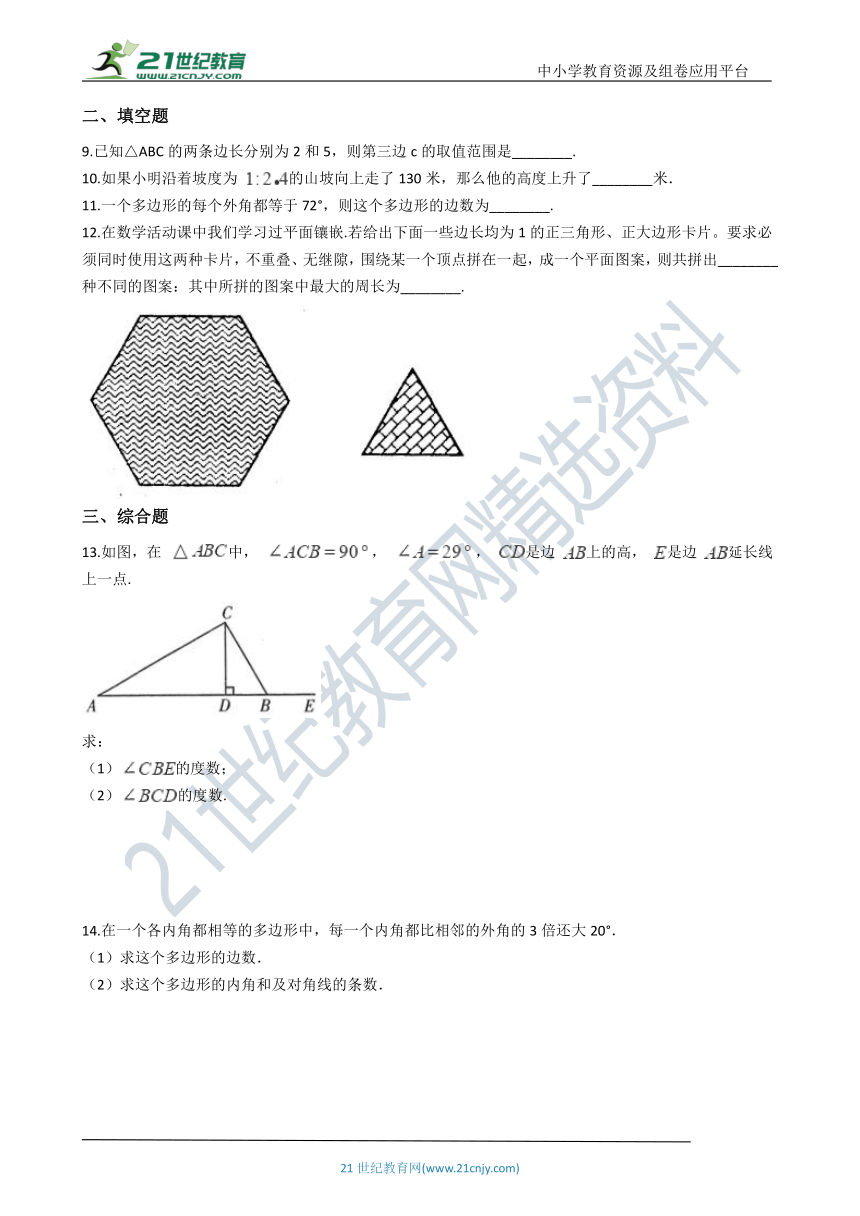
12.在数学活动课中我们学面镶嵌.若给出下面一些边长均为1的正三角形、正大边形卡片。要求必须同时使用这两种卡片,不重叠、无继隙,围绕某一个顶点拼在一起,成一个平面图案,则共拼出________种不同的图案:其中所拼的图案中最大的周长为________.
三、综合题
13.如图,在
中,
,
,
是边
上的高,
是边
延长线上一点.
求:
(1)的度数;
(2)的度数.
14.在一个各内角都相等的多边形中,每一个内角都比相邻的外角的3倍还大20°.
(1)求这个多边形的边数.
(2)求这个多边形的内角和及对角线的条数.
答案解析部分
一、单选题
1.【答案】
D
解:由题意可得:4=8-4<第三边长<4+8=12,观察选项可得:10可以为第三边长.
故答案为:D.
2.【答案】
D
解:∵AC=CD,∠A=50°,
∴∠CDA=∠A=50°.
∵CD=BD,
∴∠B=∠DCB=∠CDA=×50°=25°.
∵BD=BE,
∴∠BDE=∠BED==77.5°.
∵∠CDB=180°-∠CDA=180°-50°=130°,
∴∠CDE=∠CDB-∠BDE=130°-77.5°=52.5°.
故答案为:D.
3.【答案】
B
解:
是等边三角形,
是等腰直角三角形,
,
,
,
,
,
,
.
故答案为:B.
4.【答案】
C
解:
,
,
三角形的内角和为
.
故答案为:C.
5.【答案】
D
解:A、∵1+2=3,
∴这三根小木棒不能构成三角形,故A不符合题意;
B、∵2+4=6,
∴这三根小木棒不能构成三角形,故B不符合题意;
C、∵3+4=7<8,
∴这三根小木棒不能构成三角形,故C不符合题意;
D、∵6+8=14>10,
∴这三根小木棒能构成三角形,故D符合题意;
故答案为:D.
6.【答案】
C
解:设两内角的度数为x、4x;
当等腰三角形的顶角为x时,x+4x+4x=180°,x=20°;
当等腰三角形的顶角为4x时,4x+x+x=180°,x=30°,4x=120°;
因此等腰三角形的顶角度数为20°或120°.
故答案为:C.
7.【答案】
C
解:A、正八边形的每个内角为:180°-360°÷8=135°,正三角形的每个内角60°,135m+60n=360°,n=6-
m,显然m取任何正整数时,n不能得正整数,故不能铺满;
B、正五边形每个内角是180°-360°÷5=108°,正八边形的每个内角为:180°-360°÷8=135°,108m+135n=360°,m取任何正整数时,n不能得正整数,故不能铺满;
C、正六边形的每个内角是120°,正三角形的每个内角是60°,∵
2×120°+2×60°=360°,或120°+4×60°=360°,能铺满;
D、正六边形的每个内角是120°,正五边形每个内角是180°-360°÷5=108°,120m+108n=360°,m取任何正整数时,n不能得正整数,故不能铺满.
故答案为:C.
8.【答案】
C
解:等腰三角形的内角和是180°,能被360°整除,放在同一顶点处能够用一种图形镶嵌整个平面;
四边形的内角和是360°,能被360°整除,放在同一顶点处能够用一种图形镶嵌整个平面;
正六边形的每个内角是120°,能被360°整除,能够用一种图形镶嵌整个平面;
正五边形的每个内角是108°,不能被360°整除,放在同一顶点处不能够用一种图形镶嵌整个平面;
圆不能够用一种图形镶嵌整个平面;
综上所述,能够用一种图形镶嵌整个平面的有3个.
故答案为:C.
二、填空题
9.【答案】
3<c<7
解:由题意,得
5﹣2<c<5+2,即3<c<7.
故答案为:3<c<7.
10.【答案】
解:设高度上升了h,则水平前进了2.4h,
由勾股定理得:
,解得h=50.
故答案为50.
11.【答案】
五
解:由一个多边形的每个外角都等于72°,可得:
多边形的边数为:
,
故答案为:五.
12.【答案】
3;10
解:正六边形每个内角为120°,正三角形每个内角为60°。设一个顶点处用x个正六边形,y个正三角形。根据题意,得
120x+60y=360
解得
或
∴共有两种拼接方案,能拼出三种图形:
?
?
?????????
?????????????
图1??????????????????????
?
图2???????????????????????????????
???
??
图3
图1的周长是8;图2的周长是10;图3的周长是10。
∴最大周长是10.
三、综合题
13.【答案】
(1)∵
,
,
是
的外角,
∴
;
(2)∵
是
边上的高,
∴
.
∴
.
∵
,
,
∴
.
14.【答案】
(1)解:设多边形的一个外角为α°,则与其相邻的内角为(3α+20)°
由题意,得(3α+20)+α=180.?????????????????????????????????????????????
解得α=40,???????????????????????????????????????????????????????
即多边形的每个外角为40°.?????????????????????????????
∵多边形的外角和为360°,
∴多边形的边数为360°÷40°=9.
(2)解:这个多边形的内角和为(9-2)×180°=1260°,
对角线一共有
×(9-3)×9=27(条).?????????????????
答:这个多边形的边数为9,内角和1260°,对角线27条.
第9章测试卷
一、单选题
1.若一个三角形的两边长分别为4和8,则第三边长可以是(??????
)
A.?4?????????????????????????????????????????B.?12?????????????????????????????????????????C.?13?????????????????????????????????????????D.?10
2.如图所示,在△ABC中,D为AB上一点,E为BC上一点,且AC
=
CD
=
BD
=
BE,∠A
=
50°,则∠CDE的度数为(??
)
A.?50°?????????????????????????????????????B.?51°?????????????????????????????????????C.?51.5°?????????????????????????????????????D.?52.5°
3.如图,
是等边三角形,
是等腰直角三角形,
,连接BD,则
的度数为(??
)
A.?????????????????????????????????????B.?????????????????????????????????????C.?????????????????????????????????????D.?
4.如果在
中,
,则
等于(??
)
A.????????????????????????????????????B.????????????????????????????????????C.????????????????????????????????????D.?
5.下列长度的三根小木棒能构成三角形的是(??
)
A.?1cm,2
cm,3
cm????????????????????????????????????????????B.?2
cm,4
cm,6
cm
C.?3
cm,4
cm,8
cm???????????????????????????????????????????D.?6
cm,8
cm,10
cm
6.已知一个等腰三角形两内角的度数之比为
,则这个等腰三角形顶角的度数为(??
)
A.???????????????????????????????????B.???????????????????????????????????C.?或
??????????????????????????????????D.?
7.用下列边长相同的正多边形组合,能够铺满地面不留缝隙的是(??
)
A.?正八边形和正三角形???????????????????????????????????????????B.?正五边形和正八边形
C.?正六边形和正三角形???????????????????????????????????????????D.?正六边形和正五边形
8.如图所示的图形中,能够用一个图形镶嵌整个平面的有(?
)个
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
二、填空题
9.已知△ABC的两条边长分别为2和5,则第三边c的取值范围是________.
10.如果小明沿着坡度为
的山坡向上走了130米,那么他的高度上升了________米.
11.一个多边形的每个外角都等于72°,则这个多边形的边数为________.
12.在数学活动课中我们学面镶嵌.若给出下面一些边长均为1的正三角形、正大边形卡片。要求必须同时使用这两种卡片,不重叠、无继隙,围绕某一个顶点拼在一起,成一个平面图案,则共拼出________种不同的图案:其中所拼的图案中最大的周长为________.
三、综合题
13.如图,在
中,
,
,
是边
上的高,
是边
延长线上一点.
求:
(1)的度数;
(2)的度数.
14.在一个各内角都相等的多边形中,每一个内角都比相邻的外角的3倍还大20°.
(1)求这个多边形的边数.
(2)求这个多边形的内角和及对角线的条数.
答案解析部分
一、单选题
1.【答案】
D
解:由题意可得:4=8-4<第三边长<4+8=12,观察选项可得:10可以为第三边长.
故答案为:D.
2.【答案】
D
解:∵AC=CD,∠A=50°,
∴∠CDA=∠A=50°.
∵CD=BD,
∴∠B=∠DCB=∠CDA=×50°=25°.
∵BD=BE,
∴∠BDE=∠BED==77.5°.
∵∠CDB=180°-∠CDA=180°-50°=130°,
∴∠CDE=∠CDB-∠BDE=130°-77.5°=52.5°.
故答案为:D.
3.【答案】
B
解:
是等边三角形,
是等腰直角三角形,
,
,
,
,
,
,
.
故答案为:B.
4.【答案】
C
解:
,
,
三角形的内角和为
.
故答案为:C.
5.【答案】
D
解:A、∵1+2=3,
∴这三根小木棒不能构成三角形,故A不符合题意;
B、∵2+4=6,
∴这三根小木棒不能构成三角形,故B不符合题意;
C、∵3+4=7<8,
∴这三根小木棒不能构成三角形,故C不符合题意;
D、∵6+8=14>10,
∴这三根小木棒能构成三角形,故D符合题意;
故答案为:D.
6.【答案】
C
解:设两内角的度数为x、4x;
当等腰三角形的顶角为x时,x+4x+4x=180°,x=20°;
当等腰三角形的顶角为4x时,4x+x+x=180°,x=30°,4x=120°;
因此等腰三角形的顶角度数为20°或120°.
故答案为:C.
7.【答案】
C
解:A、正八边形的每个内角为:180°-360°÷8=135°,正三角形的每个内角60°,135m+60n=360°,n=6-
m,显然m取任何正整数时,n不能得正整数,故不能铺满;
B、正五边形每个内角是180°-360°÷5=108°,正八边形的每个内角为:180°-360°÷8=135°,108m+135n=360°,m取任何正整数时,n不能得正整数,故不能铺满;
C、正六边形的每个内角是120°,正三角形的每个内角是60°,∵
2×120°+2×60°=360°,或120°+4×60°=360°,能铺满;
D、正六边形的每个内角是120°,正五边形每个内角是180°-360°÷5=108°,120m+108n=360°,m取任何正整数时,n不能得正整数,故不能铺满.
故答案为:C.
8.【答案】
C
解:等腰三角形的内角和是180°,能被360°整除,放在同一顶点处能够用一种图形镶嵌整个平面;
四边形的内角和是360°,能被360°整除,放在同一顶点处能够用一种图形镶嵌整个平面;
正六边形的每个内角是120°,能被360°整除,能够用一种图形镶嵌整个平面;
正五边形的每个内角是108°,不能被360°整除,放在同一顶点处不能够用一种图形镶嵌整个平面;
圆不能够用一种图形镶嵌整个平面;
综上所述,能够用一种图形镶嵌整个平面的有3个.
故答案为:C.
二、填空题
9.【答案】
3<c<7
解:由题意,得
5﹣2<c<5+2,即3<c<7.
故答案为:3<c<7.
10.【答案】
解:设高度上升了h,则水平前进了2.4h,
由勾股定理得:
,解得h=50.
故答案为50.
11.【答案】
五
解:由一个多边形的每个外角都等于72°,可得:
多边形的边数为:
,
故答案为:五.
12.【答案】
3;10
解:正六边形每个内角为120°,正三角形每个内角为60°。设一个顶点处用x个正六边形,y个正三角形。根据题意,得
120x+60y=360
解得
或
∴共有两种拼接方案,能拼出三种图形:
?
?
?????????
?????????????
图1??????????????????????
?
图2???????????????????????????????
???
??
图3
图1的周长是8;图2的周长是10;图3的周长是10。
∴最大周长是10.
三、综合题
13.【答案】
(1)∵
,
,
是
的外角,
∴
;
(2)∵
是
边上的高,
∴
.
∴
.
∵
,
,
∴
.
14.【答案】
(1)解:设多边形的一个外角为α°,则与其相邻的内角为(3α+20)°
由题意,得(3α+20)+α=180.?????????????????????????????????????????????
解得α=40,???????????????????????????????????????????????????????
即多边形的每个外角为40°.?????????????????????????????
∵多边形的外角和为360°,
∴多边形的边数为360°÷40°=9.
(2)解:这个多边形的内角和为(9-2)×180°=1260°,
对角线一共有
×(9-3)×9=27(条).?????????????????
答:这个多边形的边数为9,内角和1260°,对角线27条.
