2020-2021学年七年级数学人教版下册:第五章 图形模型构建---平行线的性质与判定的应用课件 (共20张ppt)
文档属性
| 名称 | 2020-2021学年七年级数学人教版下册:第五章 图形模型构建---平行线的性质与判定的应用课件 (共20张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 412.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 21:34:47 | ||
图片预览






文档简介
(共20张PPT)
数学说题
---平行线性质判定应用
图形模型构建
如图(2),如果AB∥CD∥EF
,那么∠BAC+∠ACE+∠CEF=()
A.180°
B.270°
C.360°
D.540°
原题再现
人教版七年级下册习题5.3第7题(2)
A
B
C
D
E
F
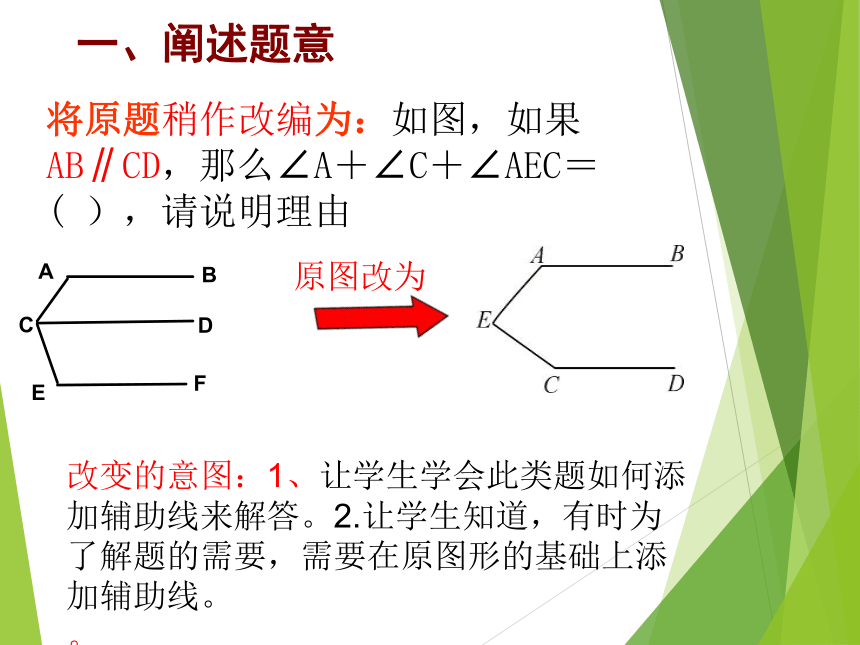
将原题稍作改编为:如图,如果AB∥CD,那么∠A+∠C+∠AEC=(
),请说明理由
一、阐述题意
原图改为
改变的意图:1、让学生学会此类题如何添加辅助线来解答。2.让学生知道,有时为了解题的需要,需要在原图形的基础上添加辅助线。
。
A
B
C
D
E
F
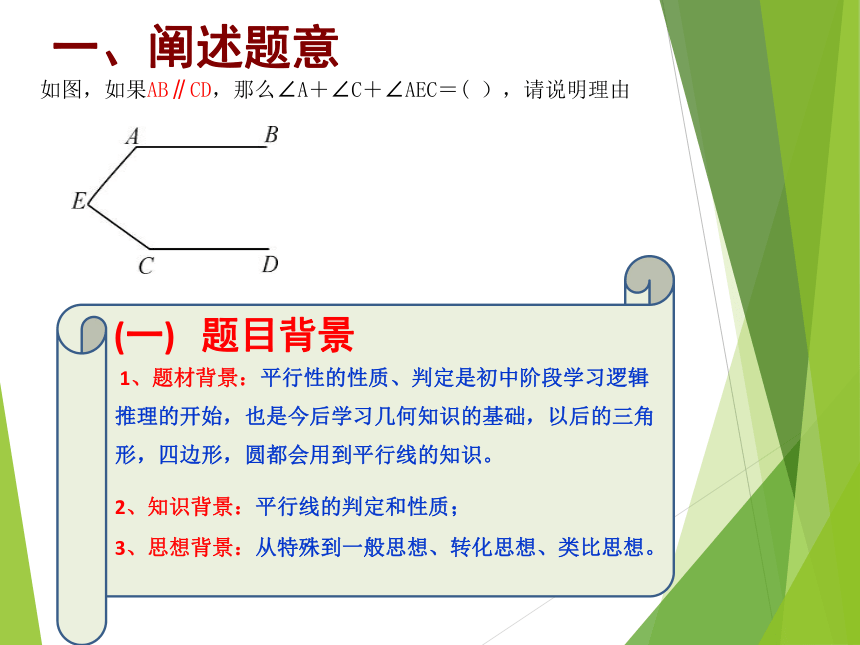
一、阐述题意
如图,如果AB∥CD,那么∠A+∠C+∠AEC=(
),请说明理由
(一)
题目背景
1、题材背景:平行性的性质、判定是初中阶段学习逻辑推理的开始,也是今后学习几何知识的基础,以后的三角形,四边形,圆都会用到平行线的知识。
2、知识背景:平行线的判定和性质;
3、思想背景:从特殊到一般思想、转化思想、类比思想。
一、阐述题意
如图,如果AB∥CD,那么∠A+∠C+∠AEC=(
),请说明理由
平行线判定和性质已学习,掌握了一定的逻辑推理说明能力,有对简单图形的识别判断和说理能力,此题重点渗透构建图形模型,应用平行线性质判定,为以后几何知识学习做准备。
学生可能会遇到的问题:(1)不能从图形中提炼出图形模型。
(2)起初想不到添加辅助线
(二)学情分析:
如图,如果AB∥CD,那么∠A+∠C+∠AEC=(
)
二、题目解答
如何解答,有教材原题铺垫,学生不难想到:
过点E分别作AB或CD的平行线,把∠BED一分为二.
解:过点E作EF
∥
AB
∵∠A+∠AEF=
180°
又∵AB∥
CD
∴EF
∥
CD
∴∠C+∠CEF=
180°
∴∠A+∠AEF+∠C+∠CEF=360°
即:
∠A+∠C+∠AEC=
360°
本题是考察学生对平行公理推论和平行线性质的掌握情况。学生在学行线的判定和性质,对推理证明题有初步的了解,但对于七年级学生还不具备逻辑思维和推理能力,要把此题有条理的写出来还是有一定难度。
学生易错点:1.添加辅助线叙述出错,如:过点E作AB、CD的平行线EF,
2.推理过程不严谨:如:过点E作EF
∥AB
所以∠A+∠AEF=180°
又因为EF∥CD
所以∠C+∠CEF=180°
EF∥CD
二、题目解答
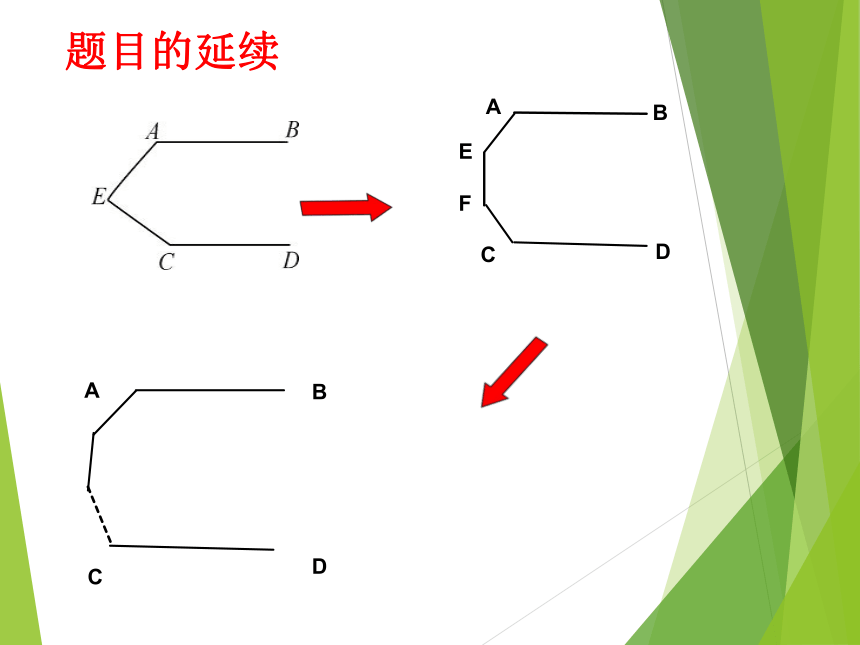
题目的延续
A
C
A
B
C
D
E
F
D
B
特殊到一般的思想
这不从特殊推广到一般了吗?
变式:
.
如图,如果AB∥CD,
那么∠A,∠C,∠E之间有怎样的数量关系?
目的:1.让学生再次感受如何添加辅助线
2.让学生无形中体会到了题目的迁移变化,感受图形的变化美,体会到数学的分类思想,类比思想
B
A
C
D
阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
三种基本图形对比
如图所示的是我们常用的折叠式小刀,其中刀柄外形可看成一个梯形挖去一个半圆,刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图所示的∠1与∠2,则∠1与∠2的度数和是 度.?
取景对比
七下同步练习册第17页第11题
分解转化“M”型
三、题目应用
取景对比
分解转化“M”型
如图,将一副三角板和一张对边平行的纸条按下方式摆放,两个三角板的一直角边重合,含30度角的直角三角板的斜边与纸条一边重合,含45度角的三角板的一个顶点在纸条的另一边上,则∠1的度数
三、题目应用
取景对比
分解转化“M”型
分解转化“铅笔头”型
转化思想
如图,矩形ABCD的顶点A、C分别在直线a、b上,且a
∥
b,
∠1
=60度,则∠2的度数为()
三、题目应用
问题情境:如图①,AB∥AB,∠PAB=130°,
∠PAB=120°,求∠APC的度数.
小明的思路是:如图22②,过点P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图③,AD∥BC,点P在射线OM上运动,当点P在A,B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD,∠α,∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A,M两点之间和B,O两点之间运动时(点P与点A,B,O三点不重合),请分别写出∠CPD,∠α,∠β之间的数量关系.
中考链接
(1)如图③,AD∥BC,点P在射线OM上运动,当点P在A,B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD,∠α,∠β之间有何数量关系?请说明理由;
中考链接
(2)在(1)的条件下,如果点P在A,M两点之间和B,O两点之间运动时(点P与点A,B,O三点不重合),请分别写出∠CPD,∠α,∠β之间的数量关系.
中考链接
点P在A,M两点之间
P
P
点P在A,M两点之间
本题设计总思路是,通过一个基本图形模型,延伸到三种基本图形模型,教会学生如何从题目中提炼出图形基本模型,把实际问题转化成这三种基本图形之一作为基本策略,进而决解问题的。渗透特殊到一般、转化化归,分类、类比等数学思想,提高学生对几何图形的分解提炼,运用能力。教会学生善于观察分析题目的内在联系,做到做一题,懂一类,会一片的目的。
四.说反思
数学的世界并不是缺少美,而是缺少对美的发现。如果你热爱数学,请多观察,多思考,多归纳总结,在数学的世界里就会“柳暗花明又一村”,在数学的世界里“海阔天高任你飞”。
五.结束语
谢谢指导!
数学说题
---平行线性质判定应用
图形模型构建
如图(2),如果AB∥CD∥EF
,那么∠BAC+∠ACE+∠CEF=()
A.180°
B.270°
C.360°
D.540°
原题再现
人教版七年级下册习题5.3第7题(2)
A
B
C
D
E
F
将原题稍作改编为:如图,如果AB∥CD,那么∠A+∠C+∠AEC=(
),请说明理由
一、阐述题意
原图改为
改变的意图:1、让学生学会此类题如何添加辅助线来解答。2.让学生知道,有时为了解题的需要,需要在原图形的基础上添加辅助线。
。
A
B
C
D
E
F
一、阐述题意
如图,如果AB∥CD,那么∠A+∠C+∠AEC=(
),请说明理由
(一)
题目背景
1、题材背景:平行性的性质、判定是初中阶段学习逻辑推理的开始,也是今后学习几何知识的基础,以后的三角形,四边形,圆都会用到平行线的知识。
2、知识背景:平行线的判定和性质;
3、思想背景:从特殊到一般思想、转化思想、类比思想。
一、阐述题意
如图,如果AB∥CD,那么∠A+∠C+∠AEC=(
),请说明理由
平行线判定和性质已学习,掌握了一定的逻辑推理说明能力,有对简单图形的识别判断和说理能力,此题重点渗透构建图形模型,应用平行线性质判定,为以后几何知识学习做准备。
学生可能会遇到的问题:(1)不能从图形中提炼出图形模型。
(2)起初想不到添加辅助线
(二)学情分析:
如图,如果AB∥CD,那么∠A+∠C+∠AEC=(
)
二、题目解答
如何解答,有教材原题铺垫,学生不难想到:
过点E分别作AB或CD的平行线,把∠BED一分为二.
解:过点E作EF
∥
AB
∵∠A+∠AEF=
180°
又∵AB∥
CD
∴EF
∥
CD
∴∠C+∠CEF=
180°
∴∠A+∠AEF+∠C+∠CEF=360°
即:
∠A+∠C+∠AEC=
360°
本题是考察学生对平行公理推论和平行线性质的掌握情况。学生在学行线的判定和性质,对推理证明题有初步的了解,但对于七年级学生还不具备逻辑思维和推理能力,要把此题有条理的写出来还是有一定难度。
学生易错点:1.添加辅助线叙述出错,如:过点E作AB、CD的平行线EF,
2.推理过程不严谨:如:过点E作EF
∥AB
所以∠A+∠AEF=180°
又因为EF∥CD
所以∠C+∠CEF=180°
EF∥CD
二、题目解答
题目的延续
A
C
A
B
C
D
E
F
D
B
特殊到一般的思想
这不从特殊推广到一般了吗?
变式:
.
如图,如果AB∥CD,
那么∠A,∠C,∠E之间有怎样的数量关系?
目的:1.让学生再次感受如何添加辅助线
2.让学生无形中体会到了题目的迁移变化,感受图形的变化美,体会到数学的分类思想,类比思想
B
A
C
D
阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
三种基本图形对比
如图所示的是我们常用的折叠式小刀,其中刀柄外形可看成一个梯形挖去一个半圆,刀片的两条边缘线可看成两条平行的线段,转动刀片时会形成如图所示的∠1与∠2,则∠1与∠2的度数和是 度.?
取景对比
七下同步练习册第17页第11题
分解转化“M”型
三、题目应用
取景对比
分解转化“M”型
如图,将一副三角板和一张对边平行的纸条按下方式摆放,两个三角板的一直角边重合,含30度角的直角三角板的斜边与纸条一边重合,含45度角的三角板的一个顶点在纸条的另一边上,则∠1的度数
三、题目应用
取景对比
分解转化“M”型
分解转化“铅笔头”型
转化思想
如图,矩形ABCD的顶点A、C分别在直线a、b上,且a
∥
b,
∠1
=60度,则∠2的度数为()
三、题目应用
问题情境:如图①,AB∥AB,∠PAB=130°,
∠PAB=120°,求∠APC的度数.
小明的思路是:如图22②,过点P作PE∥AB,通过平行线性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图③,AD∥BC,点P在射线OM上运动,当点P在A,B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD,∠α,∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A,M两点之间和B,O两点之间运动时(点P与点A,B,O三点不重合),请分别写出∠CPD,∠α,∠β之间的数量关系.
中考链接
(1)如图③,AD∥BC,点P在射线OM上运动,当点P在A,B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD,∠α,∠β之间有何数量关系?请说明理由;
中考链接
(2)在(1)的条件下,如果点P在A,M两点之间和B,O两点之间运动时(点P与点A,B,O三点不重合),请分别写出∠CPD,∠α,∠β之间的数量关系.
中考链接
点P在A,M两点之间
P
P
点P在A,M两点之间
本题设计总思路是,通过一个基本图形模型,延伸到三种基本图形模型,教会学生如何从题目中提炼出图形基本模型,把实际问题转化成这三种基本图形之一作为基本策略,进而决解问题的。渗透特殊到一般、转化化归,分类、类比等数学思想,提高学生对几何图形的分解提炼,运用能力。教会学生善于观察分析题目的内在联系,做到做一题,懂一类,会一片的目的。
四.说反思
数学的世界并不是缺少美,而是缺少对美的发现。如果你热爱数学,请多观察,多思考,多归纳总结,在数学的世界里就会“柳暗花明又一村”,在数学的世界里“海阔天高任你飞”。
五.结束语
谢谢指导!
