北师大版八年级数学下册3.3中心对称课课练(Word版,附答案)
文档属性
| 名称 | 北师大版八年级数学下册3.3中心对称课课练(Word版,附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 277.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-01 00:00:00 | ||
图片预览

文档简介
3 中心对称
知识点
1 中心对称
1.[2020·北京延庆区一模]
下列各组图形中,△A'B'C'与△ABC成中心对称的是
( )
图3-3-1
2.已知下列命题,其中正确的个数是
( )
(1)成中心对称的两个图形一定不全等;
(2)成中心对称的两个图形是全等图形;
(3)两个全等的图形一定成中心对称.
A.0
B.1
C.2
D.3
3.如图3-3-2,△ABC与△A'B'C'成中心对称,下列说法不正确的是
( )
图3-3-2
A.AB=A'B',AC∥A'C'
B.△ABC≌△A'B'C'
C.OB=OA',OC=OC'
D.∠BAO=∠B'A'O
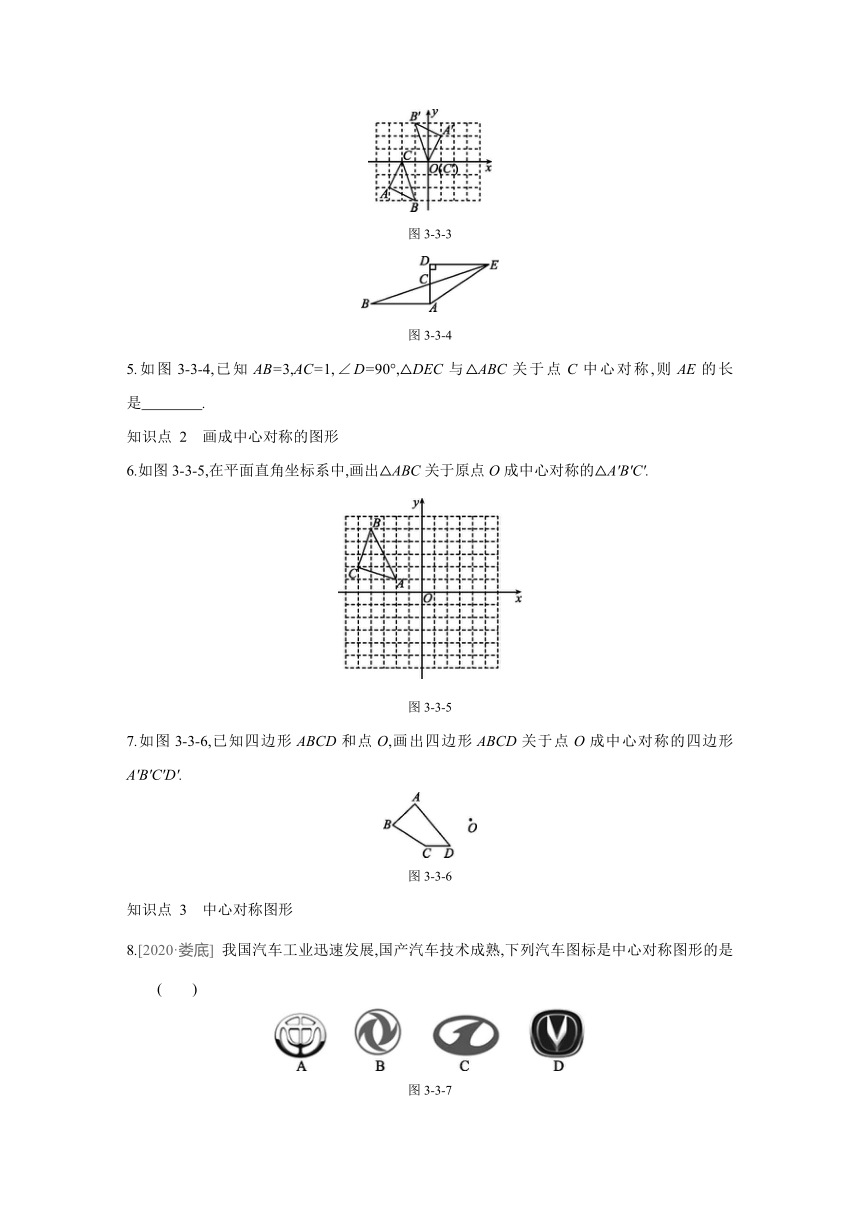
4.如图3-3-3,在平面直角坐标系xOy中,△ABC经过中心对称变换得到△A'B'C',那么对称中心的坐标为
( )
A.(0,0)
B.(-1,0)
C.(-1,-1)
D.(0,-1)
图3-3-3
图3-3-4
5.如图3-3-4,已知AB=3,AC=1,∠D=90°,△DEC与△ABC关于点C中心对称,则AE的长是 .?
知识点
2 画成中心对称的图形
6.如图3-3-5,在平面直角坐标系中,画出△ABC关于原点O成中心对称的△A'B'C'.
图3-3-5
7.如图3-3-6,已知四边形ABCD和点O,画出四边形ABCD关于点O成中心对称的四边形A'B'C'D'.
图3-3-6
知识点
3 中心对称图形
8.[2020·娄底]
我国汽车工业迅速发展,国产汽车技术成熟,下列汽车图标是中心对称图形的是
( )
图3-3-7
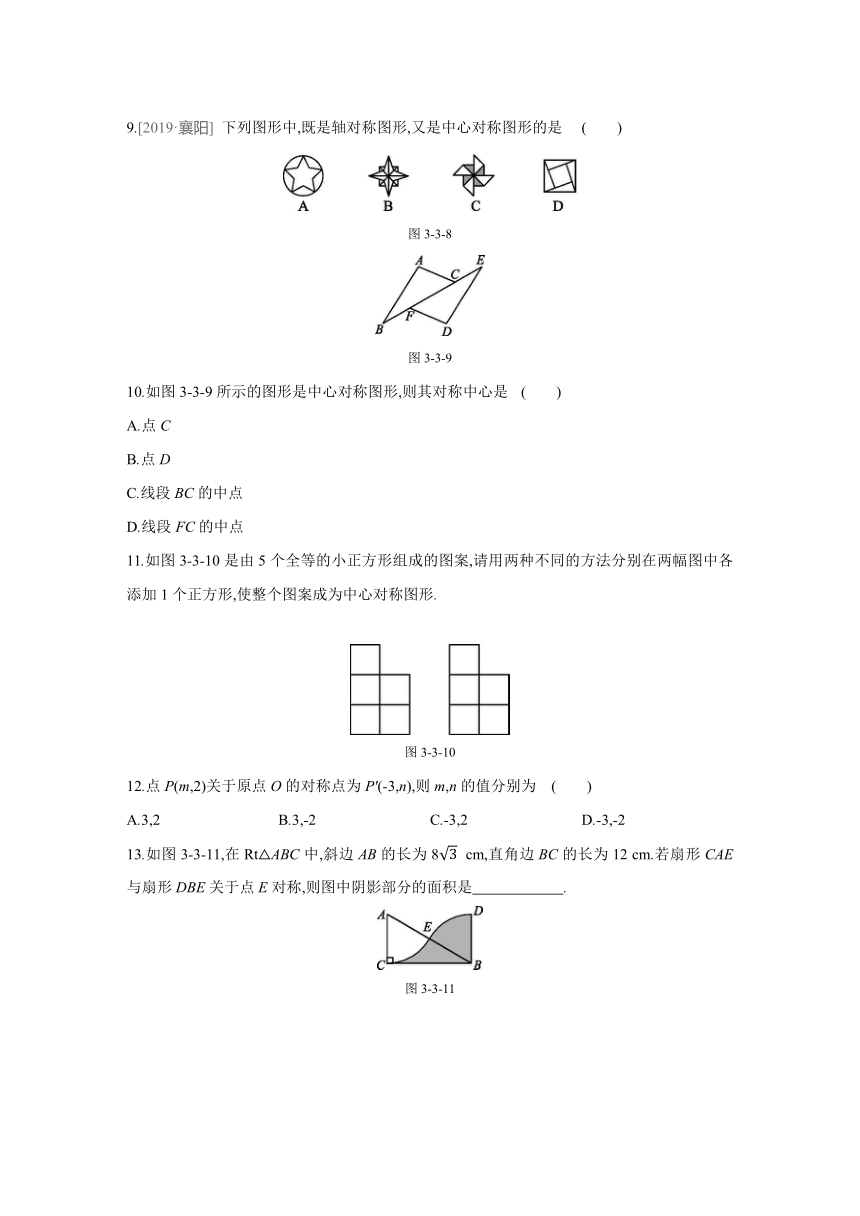
9.[2019·襄阳]
下列图形中,既是轴对称图形,又是中心对称图形的是
( )
图3-3-8
图3-3-9
10.如图3-3-9所示的图形是中心对称图形,则其对称中心是
( )
A.点C
B.点D
C.线段BC的中点
D.线段FC的中点
11.如图3-3-10是由5个全等的小正方形组成的图案,请用两种不同的方法分别在两幅图中各添加1个正方形,使整个图案成为中心对称图形.
图3-3-10
12.点P(m,2)关于原点O的对称点为P'(-3,n),则m,n的值分别为
( )
A.3,2
B.3,-2
C.-3,2
D.-3,-2
13.如图3-3-11,在Rt△ABC中,斜边AB的长为8
cm,直角边BC的长为12
cm.若扇形CAE与扇形DBE关于点E对称,则图中阴影部分的面积是 .?
图3-3-11
图3-3-12
14.如图3-3-12是4×4的正方形网格,把其中一个标有数字的白色小正方形涂上阴影,就可以使图中的阴影部分构成一个中心对称图形,则这个白色小正方形内的数字是 .?
15.如图3-3-13所示,正方形ABCD与正方形A1B1C1D1关于某点对称.已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
图3-3-13
16.数学兴趣小组活动时,老师提出了如下问题:
(1)如图3-3-14(a),在△ABC中,若AB=5,AC=3,求BC边上的中线AD长的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:将△ACD绕点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中,利用三角形的三边关系可得2(2)解决问题:受到(1)的启发,请你证明下列命题:如图(b),在△ABC中,D是BC边的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;
②若∠A=90°,探索线段BE,CF,EF之间的等量关系,并加以证明.
图3-3-14
教师详解详析
1.D
2.B [解析]
成中心对称的两个图形一定全等,两个全等的图形不一定成中心对称,故只有(2)说法正确.
3.C
4.B
5. [解析]
∵△DEC与△ABC关于点C中心对称,∴DC=AC=1,DE=AB=3,点D,C,A在同一条直线上,∴在Rt△EDA中,AE==.
6.解:△A'B'C'如图所示.
7.解:四边形A'B'C'D'如图所示.
8.B 9.B 10.D
11.解:如图所示:
12.B
13.24
cm2
14.3
15.解:(1)∵正方形ABCD与正方形A1B1C1D1关于某点对称,
∴D,D1是对应点,
∴DD1的中点是对称中心.
∵D(0,2),D1(0,3),
∴对称中心的坐标为(0,2.5).
(2)B(-2,4),C(-2,2),B1(2,1),C1(2,3).
16.解:(2)①证明:如图,将△CFD绕点D逆时针旋转180°得到△BGD,连接EG,
∴CF=BG,DF=DG.
又∵DE⊥DF,
∴EF=EG.
在△BEG中,BE+BG>EG,
∴BE+CF>EF.
②BE2+CF2=EF2.
证明:若∠A=90°,则∠EBC+∠FCB=90°.
由①知∠FCD=∠DBG,EF=EG,BG=CF,
∴∠EBC+∠DBG=90°,即∠EBG=90°,
∴在Rt△EBG中,BE2+BG2=EG2,
∴BE2+CF2=EF2.
知识点
1 中心对称
1.[2020·北京延庆区一模]
下列各组图形中,△A'B'C'与△ABC成中心对称的是
( )
图3-3-1
2.已知下列命题,其中正确的个数是
( )
(1)成中心对称的两个图形一定不全等;
(2)成中心对称的两个图形是全等图形;
(3)两个全等的图形一定成中心对称.
A.0
B.1
C.2
D.3
3.如图3-3-2,△ABC与△A'B'C'成中心对称,下列说法不正确的是
( )
图3-3-2
A.AB=A'B',AC∥A'C'
B.△ABC≌△A'B'C'
C.OB=OA',OC=OC'
D.∠BAO=∠B'A'O
4.如图3-3-3,在平面直角坐标系xOy中,△ABC经过中心对称变换得到△A'B'C',那么对称中心的坐标为
( )
A.(0,0)
B.(-1,0)
C.(-1,-1)
D.(0,-1)
图3-3-3
图3-3-4
5.如图3-3-4,已知AB=3,AC=1,∠D=90°,△DEC与△ABC关于点C中心对称,则AE的长是 .?
知识点
2 画成中心对称的图形
6.如图3-3-5,在平面直角坐标系中,画出△ABC关于原点O成中心对称的△A'B'C'.
图3-3-5
7.如图3-3-6,已知四边形ABCD和点O,画出四边形ABCD关于点O成中心对称的四边形A'B'C'D'.
图3-3-6
知识点
3 中心对称图形
8.[2020·娄底]
我国汽车工业迅速发展,国产汽车技术成熟,下列汽车图标是中心对称图形的是
( )
图3-3-7
9.[2019·襄阳]
下列图形中,既是轴对称图形,又是中心对称图形的是
( )
图3-3-8
图3-3-9
10.如图3-3-9所示的图形是中心对称图形,则其对称中心是
( )
A.点C
B.点D
C.线段BC的中点
D.线段FC的中点
11.如图3-3-10是由5个全等的小正方形组成的图案,请用两种不同的方法分别在两幅图中各添加1个正方形,使整个图案成为中心对称图形.
图3-3-10
12.点P(m,2)关于原点O的对称点为P'(-3,n),则m,n的值分别为
( )
A.3,2
B.3,-2
C.-3,2
D.-3,-2
13.如图3-3-11,在Rt△ABC中,斜边AB的长为8
cm,直角边BC的长为12
cm.若扇形CAE与扇形DBE关于点E对称,则图中阴影部分的面积是 .?
图3-3-11
图3-3-12
14.如图3-3-12是4×4的正方形网格,把其中一个标有数字的白色小正方形涂上阴影,就可以使图中的阴影部分构成一个中心对称图形,则这个白色小正方形内的数字是 .?
15.如图3-3-13所示,正方形ABCD与正方形A1B1C1D1关于某点对称.已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标;
(2)写出顶点B,C,B1,C1的坐标.
图3-3-13
16.数学兴趣小组活动时,老师提出了如下问题:
(1)如图3-3-14(a),在△ABC中,若AB=5,AC=3,求BC边上的中线AD长的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:将△ACD绕点D逆时针旋转180°得到△EBD,把AB,AC,2AD集中在△ABE中,利用三角形的三边关系可得2
①求证:BE+CF>EF;
②若∠A=90°,探索线段BE,CF,EF之间的等量关系,并加以证明.
图3-3-14
教师详解详析
1.D
2.B [解析]
成中心对称的两个图形一定全等,两个全等的图形不一定成中心对称,故只有(2)说法正确.
3.C
4.B
5. [解析]
∵△DEC与△ABC关于点C中心对称,∴DC=AC=1,DE=AB=3,点D,C,A在同一条直线上,∴在Rt△EDA中,AE==.
6.解:△A'B'C'如图所示.
7.解:四边形A'B'C'D'如图所示.
8.B 9.B 10.D
11.解:如图所示:
12.B
13.24
cm2
14.3
15.解:(1)∵正方形ABCD与正方形A1B1C1D1关于某点对称,
∴D,D1是对应点,
∴DD1的中点是对称中心.
∵D(0,2),D1(0,3),
∴对称中心的坐标为(0,2.5).
(2)B(-2,4),C(-2,2),B1(2,1),C1(2,3).
16.解:(2)①证明:如图,将△CFD绕点D逆时针旋转180°得到△BGD,连接EG,
∴CF=BG,DF=DG.
又∵DE⊥DF,
∴EF=EG.
在△BEG中,BE+BG>EG,
∴BE+CF>EF.
②BE2+CF2=EF2.
证明:若∠A=90°,则∠EBC+∠FCB=90°.
由①知∠FCD=∠DBG,EF=EG,BG=CF,
∴∠EBC+∠DBG=90°,即∠EBG=90°,
∴在Rt△EBG中,BE2+BG2=EG2,
∴BE2+CF2=EF2.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
