上海市浦东新区第四教育署2020-2021学年七年级第二学期调研数学试卷(3月份)(五四学制)(word版含图片答案)
文档属性
| 名称 | 上海市浦东新区第四教育署2020-2021学年七年级第二学期调研数学试卷(3月份)(五四学制)(word版含图片答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 281.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-02 00:00:00 | ||
图片预览


文档简介
2020-2021学年上海市浦东新区第四教育署七年级(下)调研数学试卷(3月份)(五四学制)
一、单项选择题(本大题共有6小题,每题2分,共12分)
1.下列实数中,有理数是( )
A. B. C. D.
2.下列整数中,与最接近的是( )
A.2 B.3 C.6 D.8
3.下列运算一定正确的是( )
A. B. C.=3 D.
4.下列语句正确是( )
A.无限小数是无理数
B.无理数是无限小数
C.实数分为正实数和负实数
D.两个无理数的和还是无理数
5.如图,AB和CD相交于点O,则下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3 C.∠3=∠4 D.∠1=∠5
6.下列图形中,线段PQ的长表示点P到直线MN的距离是( )
A. B.
C. D.
二、填空题(本大题共有12小题,每题3分,共36分)
7.49的平方根是 .
8.化简:= .
9.计算:= .
10.比较大小:﹣π ﹣3.14(选填“>”、“=”、“<”).
11.近似数0.0730的有效数字有 个.
12.把化成幂的形式是 .
13.已知|a+1|+=0,则ab= .
14.的整数部分是a,小数部分是b,计算a﹣2b的值是 .
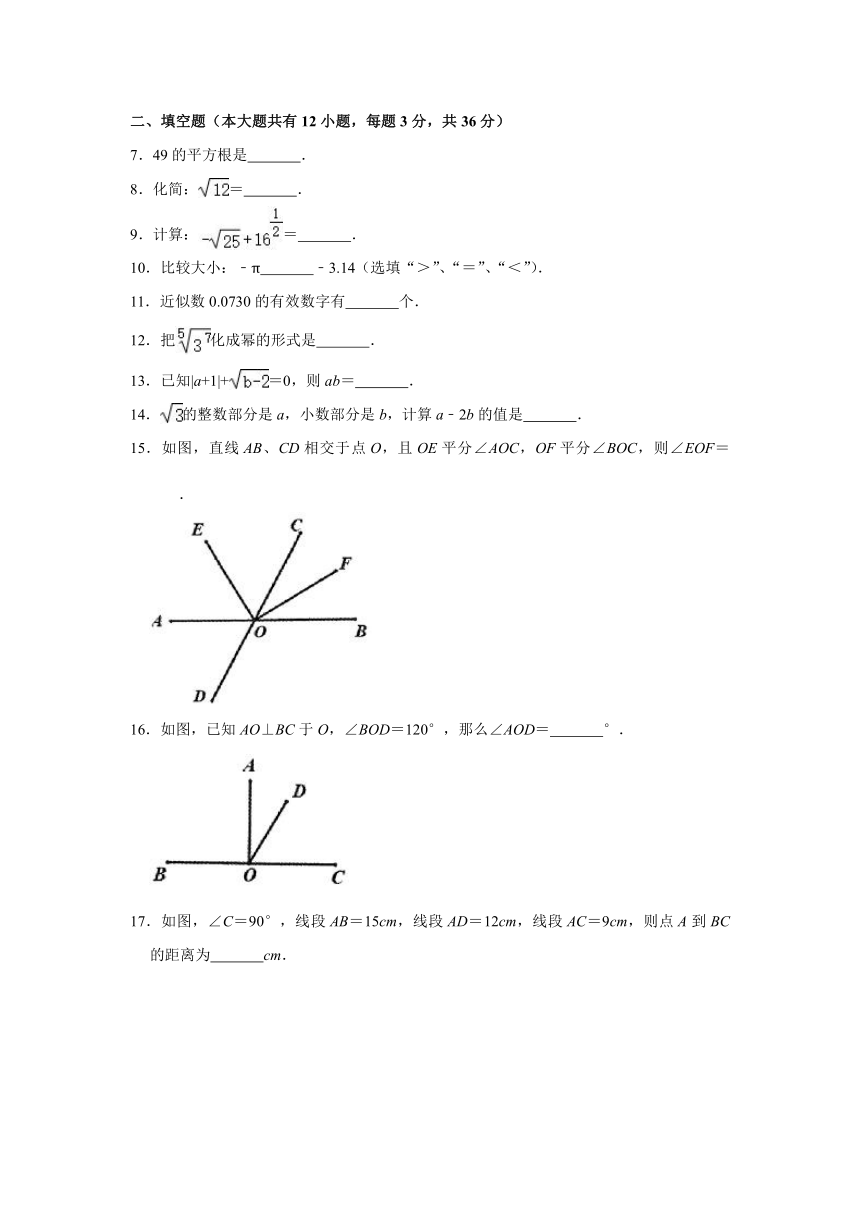
15.如图,直线AB、CD相交于点O,且OE平分∠AOC,OF平分∠BOC,则∠EOF= .
16.如图,已知AO⊥BC于O,∠BOD=120°,那么∠AOD= °.
17.如图,∠C=90°,线段AB=15cm,线段AD=12cm,线段AC=9cm,则点A到BC的距离为 cm.
18.实数a、b在数轴上所对应的点如图所示,则|﹣b|+|a+|+的值 .
三、解答题(本大题共8小题,第19至23题每题5分,第24分每题7分,第25、26题每题10分,共52分)
19.计算:.
20.计算:﹣﹣.
21.计算:.
22.利用幂的性质进行计算:(结果表示为含幂的形式).
23.如图,要把河中的水引到水池A中,应在河岸B处开始挖渠才能使水渠的长度最短,请作出图形,并说明这样做依据的几何学原理.
24.已知(2m﹣1)2=9,(n+1)3=27.求2m+n的算术平方根.
25.如图,直线AB、CD相交于点O,∠AOD=2∠AOC,OE平分∠BOD,OF平分∠COE.
(1)求∠DOE的度数;
(2)求∠AOF的度数.
26.阅读理解题:
定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:(2+i)+(3﹣4i)=5﹣3i.
(1)填空:i3= ,i4= .
(2)计算:①(2+i)(2﹣i);②(2+i)2;
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下面问题:
已知:(x+y)+3i=(1﹣x)﹣yi,(x,y为实数),求x,y的值.
一、单项选择题(本大题共有6小题,每题2分,共12分)
1.下列实数中,有理数是( )
A. B. C. D.
2.下列整数中,与最接近的是( )
A.2 B.3 C.6 D.8
3.下列运算一定正确的是( )
A. B. C.=3 D.
4.下列语句正确是( )
A.无限小数是无理数
B.无理数是无限小数
C.实数分为正实数和负实数
D.两个无理数的和还是无理数
5.如图,AB和CD相交于点O,则下列结论正确的是( )
A.∠1=∠2 B.∠2=∠3 C.∠3=∠4 D.∠1=∠5
6.下列图形中,线段PQ的长表示点P到直线MN的距离是( )
A. B.
C. D.
二、填空题(本大题共有12小题,每题3分,共36分)
7.49的平方根是 .
8.化简:= .
9.计算:= .
10.比较大小:﹣π ﹣3.14(选填“>”、“=”、“<”).
11.近似数0.0730的有效数字有 个.
12.把化成幂的形式是 .
13.已知|a+1|+=0,则ab= .
14.的整数部分是a,小数部分是b,计算a﹣2b的值是 .
15.如图,直线AB、CD相交于点O,且OE平分∠AOC,OF平分∠BOC,则∠EOF= .
16.如图,已知AO⊥BC于O,∠BOD=120°,那么∠AOD= °.
17.如图,∠C=90°,线段AB=15cm,线段AD=12cm,线段AC=9cm,则点A到BC的距离为 cm.
18.实数a、b在数轴上所对应的点如图所示,则|﹣b|+|a+|+的值 .
三、解答题(本大题共8小题,第19至23题每题5分,第24分每题7分,第25、26题每题10分,共52分)
19.计算:.
20.计算:﹣﹣.
21.计算:.
22.利用幂的性质进行计算:(结果表示为含幂的形式).
23.如图,要把河中的水引到水池A中,应在河岸B处开始挖渠才能使水渠的长度最短,请作出图形,并说明这样做依据的几何学原理.
24.已知(2m﹣1)2=9,(n+1)3=27.求2m+n的算术平方根.
25.如图,直线AB、CD相交于点O,∠AOD=2∠AOC,OE平分∠BOD,OF平分∠COE.
(1)求∠DOE的度数;
(2)求∠AOF的度数.
26.阅读理解题:
定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:(2+i)+(3﹣4i)=5﹣3i.
(1)填空:i3= ,i4= .
(2)计算:①(2+i)(2﹣i);②(2+i)2;
(3)若两个复数相等,则它们的实部和虚部必须分别相等,完成下面问题:
已知:(x+y)+3i=(1﹣x)﹣yi,(x,y为实数),求x,y的值.
同课章节目录
