10.4 线段的垂直平分线课件(共19张PPT)
文档属性
| 名称 | 10.4 线段的垂直平分线课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-03 19:04:54 | ||
图片预览




文档简介
第十章 三角形的有关证明
4 线段的垂直平分线
知识点一 线段垂直平分线的性质定理
内容
应用格式
注意问题
线段垂直平分线的性质定理
知识点一 线段垂直平分线的性质定理
内容
应用格式
注意问题
线段垂直平分线的性质定理
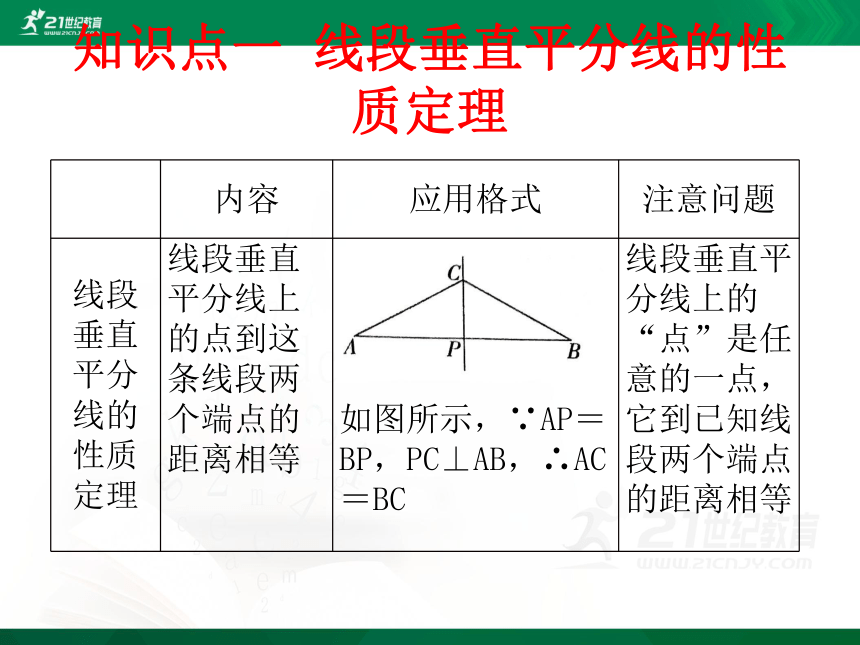
线段垂直平分线上的点到这条线段两个端点的距离相等
如图所示,∵AP=BP,PC⊥AB,∴AC=BC
线段垂直平分线上的“点”是任意的一点,它到已知线段两个端点的距离相等
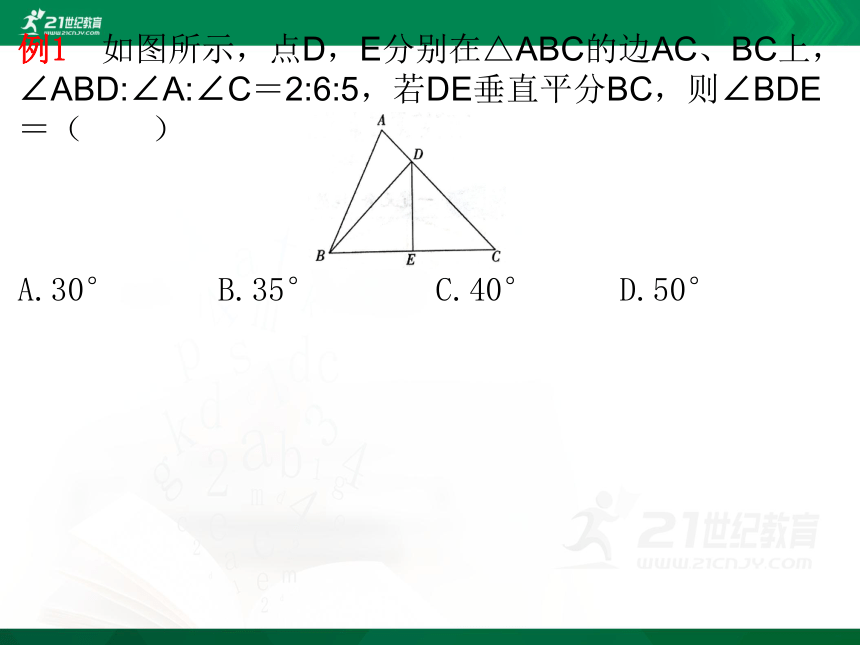
例1 如图所示,点D,E分别在△ABC的边AC、BC上,∠ABD:∠A:∠C=2:6:5,若DE垂直平分BC,则∠BDE=( )
A.30° B.35° C.40° D.50°
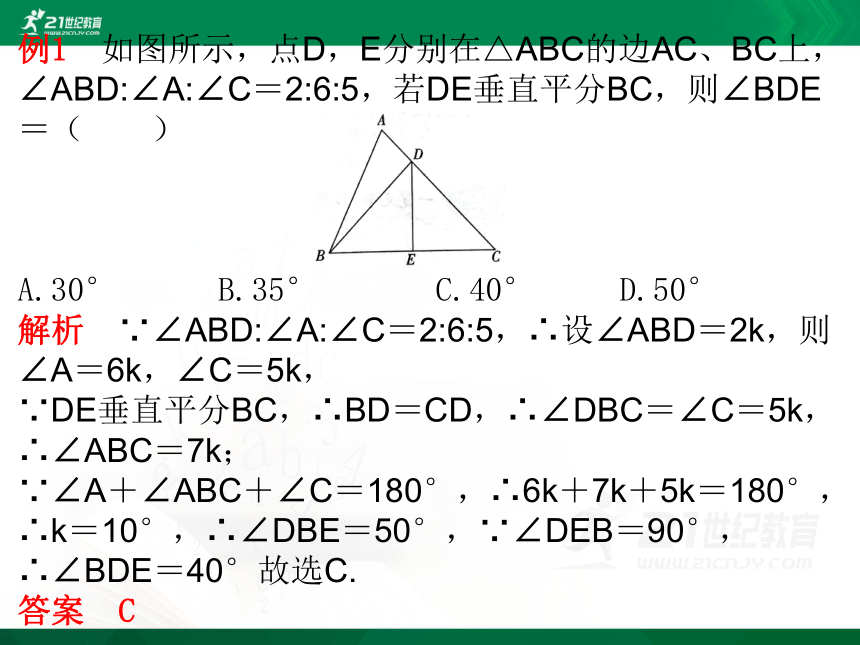
例1 如图所示,点D,E分别在△ABC的边AC、BC上,∠ABD:∠A:∠C=2:6:5,若DE垂直平分BC,则∠BDE=( )
A.30° B.35° C.40° D.50°
解析 ∵∠ABD:∠A:∠C=2:6:5,∴设∠ABD=2k,则∠A=6k,∠C=5k,
∵DE垂直平分BC,∴BD=CD,∴∠DBC=∠C=5k,∴∠ABC=7k;
∵∠A+∠ABC+∠C=180°,∴6k+7k+5k=180°,∴k=10°,∴∠DBE=50°,∵∠DEB=90°,∴∠BDE=40°故选C.
答案 C
知识点二 线段垂直平分线的判定定理
内容
应用格式
注意问题
线段垂直平分线的判定定理
知识点二 线段垂直平分线的判定定理
内容
应用格式
注意问题
线段垂直平分线的判定定理
到线段两个端点距离相等的点在这条线段的垂直平分线上
如图所示;AC=BC,∴点C在线段AB的垂直平分线上
(1)要想证明一条直线是一条线段的垂直平分线,只要证明这条直线上任意一点到这条线段的两个端点的距离相等即可
(2)区分线段垂直平分线的性质定理和判定定理,关键在于区分它们的条件和结论
例2 如图所示,在Rt△ABC中,∠C=90°,∠B=30°,AD为∠BAC的平分线.求证:点D在线段AB的垂直平分线上.
例2 如图所示,在Rt△ABC中,∠C=90°,∠B=30°,AD为∠BAC的平分线.求证:点D在线段AB的垂直平分线上.
证明 在Rt△ABC中,∠C=90°,∠B=30°,∴∠BAC=90°-∠B=60°,
∵AD为∠BAC的平分线,∴∠BAD=∠BAC=30°,∴∠B=∠BAD,∴BD=AD,
∴点D在线段AB的垂直平分线上.
知识点三 三角形三条边的垂直平分线的性质
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
知识点三 三角形三条边的垂直平分线的性质
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
注意
到线段两个端点距离相等的点有无数个,它们组成了线段的垂直平分线,但是到三角形三个顶点距离相等的点只有一个.
经典例题
题型一 运用线段垂直平分线的性质求线段的长或角的度数
例1 如图所示,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,∠B=30°,∠BAC=80°,且BC+AC=12cm.
(1)求∠CAE的度数;(2)求△AEC的周长.
题型一 运用线段垂直平分线的性质求线段的长或角的度数
解析(1)∵AB的垂直平分线分别交AB,BC于点D,E,
∴BE=AE,∴∠BAE=∠B=30°,
又∵∠BAC=80°,
∴∠CAE=∠BAC-∠BAE=80°-30°=50°.
(2)∵AE=BE,
∴AE+EC+AC=BE+EC+AC=BC+AC=12cm.
故△AEC的周长为12cm.
题型一 运用线段垂直平分线的性质求线段的长或角的度数
点拨
线段垂直平分线的性质定理是证明两条线段相等的重要依据,在证明线段相等时,不必再证明两个三角形全等,可直接运用该定理得到线段相等的结论.
题型二 线段垂直平分线的性质及判定的综合应用
例2 如图所示,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,求△ADE的周长;
(2)设直线DM、EN交于点O.
①试判断点O是否在BC的垂直平分线上,并说明理由;
②若∠BAC=100°,求∠BOC的度数.
解析
(1)∵AB、AC的垂直平分线分别交BC于D、E,∴AD=BD,AE=CE,
△ADE的周长=AD+DE+AE=BD+DE+CE=BC=10.
(2)①如图所示,点O在BC的垂直平分线上,理由:连接AO,BO,CO,
∵DM,EN分别是AB,AC的垂直平分线,
∴AO=BO,OA=OC,∴OB=OC,∴点O在BC的垂直平分线上.
②∵OM⊥AB,ON⊥AC,∴∠AMO=∠ANO=90°,∵∠BAC=100°,∴∠MON=360°-90°-90°-100°=80°,
易知∠AOM=∠BOM,∠AON=∠CON,
∴∠BOC=2∠MON=160°.
点拔
本题综合应用了线段垂直平分线的性质和判定,要注意两者的区别.
4 线段的垂直平分线
知识点一 线段垂直平分线的性质定理
内容
应用格式
注意问题
线段垂直平分线的性质定理
知识点一 线段垂直平分线的性质定理
内容
应用格式
注意问题
线段垂直平分线的性质定理
线段垂直平分线上的点到这条线段两个端点的距离相等
如图所示,∵AP=BP,PC⊥AB,∴AC=BC
线段垂直平分线上的“点”是任意的一点,它到已知线段两个端点的距离相等
例1 如图所示,点D,E分别在△ABC的边AC、BC上,∠ABD:∠A:∠C=2:6:5,若DE垂直平分BC,则∠BDE=( )
A.30° B.35° C.40° D.50°
例1 如图所示,点D,E分别在△ABC的边AC、BC上,∠ABD:∠A:∠C=2:6:5,若DE垂直平分BC,则∠BDE=( )
A.30° B.35° C.40° D.50°
解析 ∵∠ABD:∠A:∠C=2:6:5,∴设∠ABD=2k,则∠A=6k,∠C=5k,
∵DE垂直平分BC,∴BD=CD,∴∠DBC=∠C=5k,∴∠ABC=7k;
∵∠A+∠ABC+∠C=180°,∴6k+7k+5k=180°,∴k=10°,∴∠DBE=50°,∵∠DEB=90°,∴∠BDE=40°故选C.
答案 C
知识点二 线段垂直平分线的判定定理
内容
应用格式
注意问题
线段垂直平分线的判定定理
知识点二 线段垂直平分线的判定定理
内容
应用格式
注意问题
线段垂直平分线的判定定理
到线段两个端点距离相等的点在这条线段的垂直平分线上
如图所示;AC=BC,∴点C在线段AB的垂直平分线上
(1)要想证明一条直线是一条线段的垂直平分线,只要证明这条直线上任意一点到这条线段的两个端点的距离相等即可
(2)区分线段垂直平分线的性质定理和判定定理,关键在于区分它们的条件和结论
例2 如图所示,在Rt△ABC中,∠C=90°,∠B=30°,AD为∠BAC的平分线.求证:点D在线段AB的垂直平分线上.
例2 如图所示,在Rt△ABC中,∠C=90°,∠B=30°,AD为∠BAC的平分线.求证:点D在线段AB的垂直平分线上.
证明 在Rt△ABC中,∠C=90°,∠B=30°,∴∠BAC=90°-∠B=60°,
∵AD为∠BAC的平分线,∴∠BAD=∠BAC=30°,∴∠B=∠BAD,∴BD=AD,
∴点D在线段AB的垂直平分线上.
知识点三 三角形三条边的垂直平分线的性质
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
知识点三 三角形三条边的垂直平分线的性质
三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等.
注意
到线段两个端点距离相等的点有无数个,它们组成了线段的垂直平分线,但是到三角形三个顶点距离相等的点只有一个.
经典例题
题型一 运用线段垂直平分线的性质求线段的长或角的度数
例1 如图所示,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,∠B=30°,∠BAC=80°,且BC+AC=12cm.
(1)求∠CAE的度数;(2)求△AEC的周长.
题型一 运用线段垂直平分线的性质求线段的长或角的度数
解析(1)∵AB的垂直平分线分别交AB,BC于点D,E,
∴BE=AE,∴∠BAE=∠B=30°,
又∵∠BAC=80°,
∴∠CAE=∠BAC-∠BAE=80°-30°=50°.
(2)∵AE=BE,
∴AE+EC+AC=BE+EC+AC=BC+AC=12cm.
故△AEC的周长为12cm.
题型一 运用线段垂直平分线的性质求线段的长或角的度数
点拨
线段垂直平分线的性质定理是证明两条线段相等的重要依据,在证明线段相等时,不必再证明两个三角形全等,可直接运用该定理得到线段相等的结论.
题型二 线段垂直平分线的性质及判定的综合应用
例2 如图所示,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,求△ADE的周长;
(2)设直线DM、EN交于点O.
①试判断点O是否在BC的垂直平分线上,并说明理由;
②若∠BAC=100°,求∠BOC的度数.
解析
(1)∵AB、AC的垂直平分线分别交BC于D、E,∴AD=BD,AE=CE,
△ADE的周长=AD+DE+AE=BD+DE+CE=BC=10.
(2)①如图所示,点O在BC的垂直平分线上,理由:连接AO,BO,CO,
∵DM,EN分别是AB,AC的垂直平分线,
∴AO=BO,OA=OC,∴OB=OC,∴点O在BC的垂直平分线上.
②∵OM⊥AB,ON⊥AC,∴∠AMO=∠ANO=90°,∵∠BAC=100°,∴∠MON=360°-90°-90°-100°=80°,
易知∠AOM=∠BOM,∠AON=∠CON,
∴∠BOC=2∠MON=160°.
点拔
本题综合应用了线段垂直平分线的性质和判定,要注意两者的区别.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
