9.4矩形、菱形、正方形同步练习(Word版 含答案)
文档属性
| 名称 | 9.4矩形、菱形、正方形同步练习(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 399.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-02 10:54:47 | ||
图片预览


文档简介
9.4矩形、菱形、正方形同步练习
一、选择题
1.下列说法正确的是 )
A.有一个角是直角的平行四边形是正方形 B.对角线互相垂直的矩形是正方形
C.有一组邻边相等的菱形是正方形 D.各边都相等的四边形是正方形
2.已知四边形ABCD是平行四边形,下列说法正确的有( )
①当AB=BC时,它是矩形②AC⊥BD时,它是菱形
③当∠ABC=90°时,它是菱形④当AC=BD时,它是正方形
A.①② B.② C.②④ D.③④
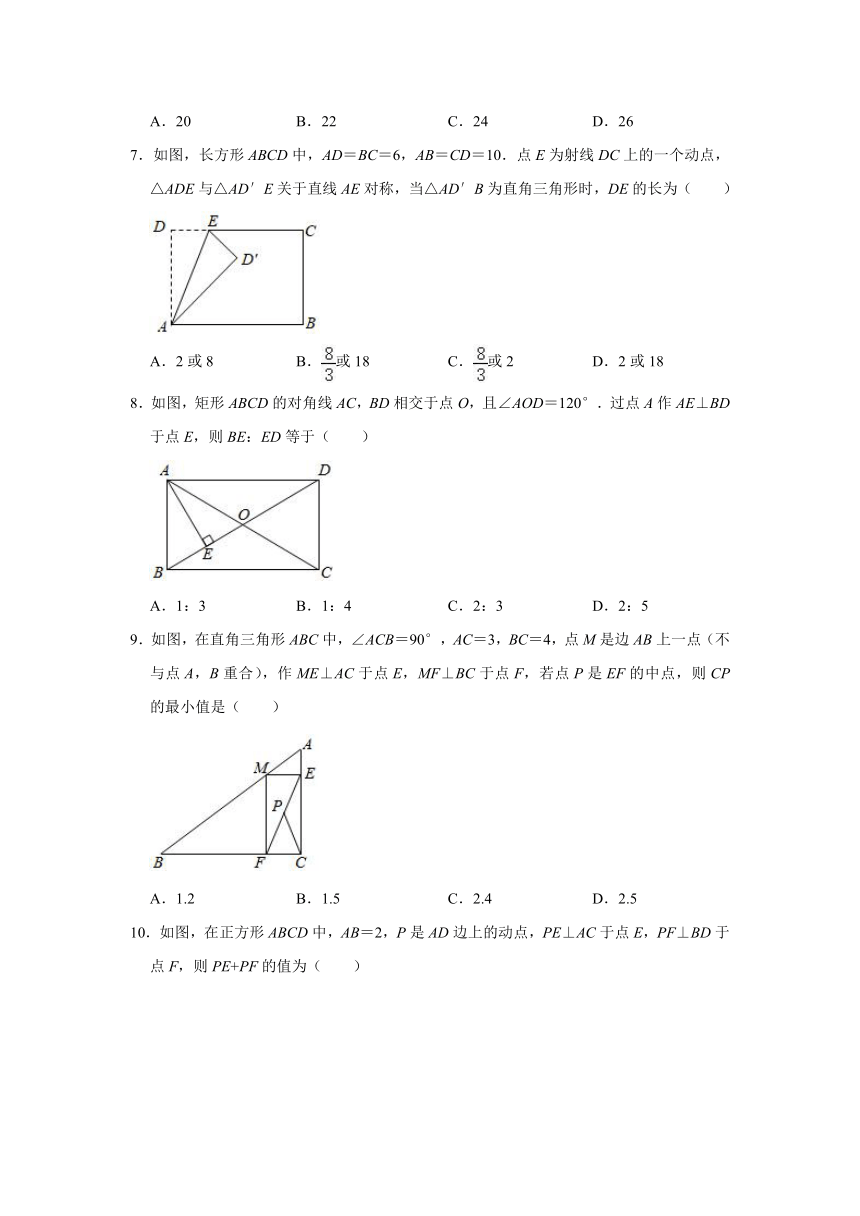
3.如图,在矩形ABCD中,AB=5,AD=12,对角线BD的垂直平分线分别与AD,BC边交于点E、F,则四边形BFDE的面积为( )
A. B. C. D.
4.如图,矩形ABCD中,AB=2,点E在边AD上,EB平分∠AEC,∠DCE=45°,则AE长( )
A. B.2﹣2 C.2﹣ D.2
5.下列性质中,菱形具有而矩形不一定具有的是( )
A.对角线相等 B.对角线垂直 C.邻边垂直 D.邻角互补
6.如图,在长方形ABCD中,AE平分∠BAD交BC于点E,连接ED,若ED=5,EC=3,则长方形的周长为( )
A.20 B.22 C.24 D.26
7.如图,长方形ABCD中,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为( )
A.2或8 B.或18 C.或2 D.2或18
8.如图,矩形ABCD的对角线AC,BD相交于点O,且∠AOD=120°.过点A作AE⊥BD于点E,则BE:ED等于( )
A.1:3 B.1:4 C.2:3 D.2:5
9.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
10.如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.4 B.2 C. D.2
二、填空题
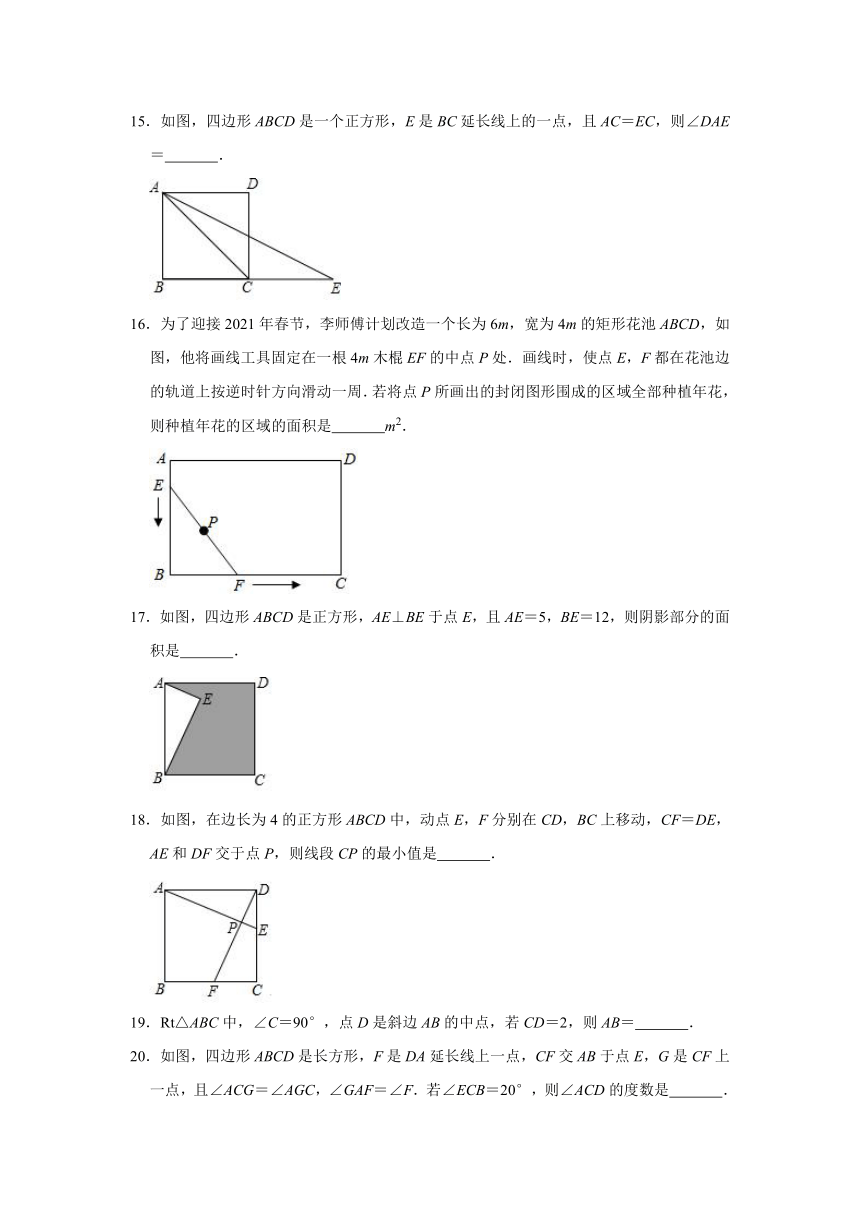
11.如图,在矩形ABCD中,对角线AC,BD交于点O,过点C作CE⊥CA,交BD的延长线于点E,若AB=2,BC=4,则DE的长为 .
12.如图,在△ABC中,AB=AC,∠BAC=40°,以AB为边作正方形ABDE,连接CE,则∠AEC= .
13.如图,在菱形ABCD中,∠B=60°,E,H分别为AB,BC的中点,G,F分别为线段HD,CE的中点.若线段FG的长为2?,则AB的长为 .
14.在长方形ABCD中,AB=,BC=4,CE=CF,延长AB至点E,连接CE,CF平分∠ECD,则BE= .
15.如图,四边形ABCD是一个正方形,E是BC延长线上的一点,且AC=EC,则∠DAE= .
16.为了迎接2021年春节,李师傅计划改造一个长为6m,宽为4m的矩形花池ABCD,如图,他将画线工具固定在一根4m木棍EF的中点P处.画线时,使点E,F都在花池边的轨道上按逆时针方向滑动一周.若将点P所画出的封闭图形围成的区域全部种植年花,则种植年花的区域的面积是 m2.
17.如图,四边形ABCD是正方形,AE⊥BE于点E,且AE=5,BE=12,则阴影部分的面积是 .
18.如图,在边长为4的正方形ABCD中,动点E,F分别在CD,BC上移动,CF=DE,AE和DF交于点P,则线段CP的最小值是 .
19.Rt△ABC中,∠C=90°,点D是斜边AB的中点,若CD=2,则AB= .
20.如图,四边形ABCD是长方形,F是DA延长线上一点,CF交AB于点E,G是CF上一点,且∠ACG=∠AGC,∠GAF=∠F.若∠ECB=20°,则∠ACD的度数是 .
三、解答题
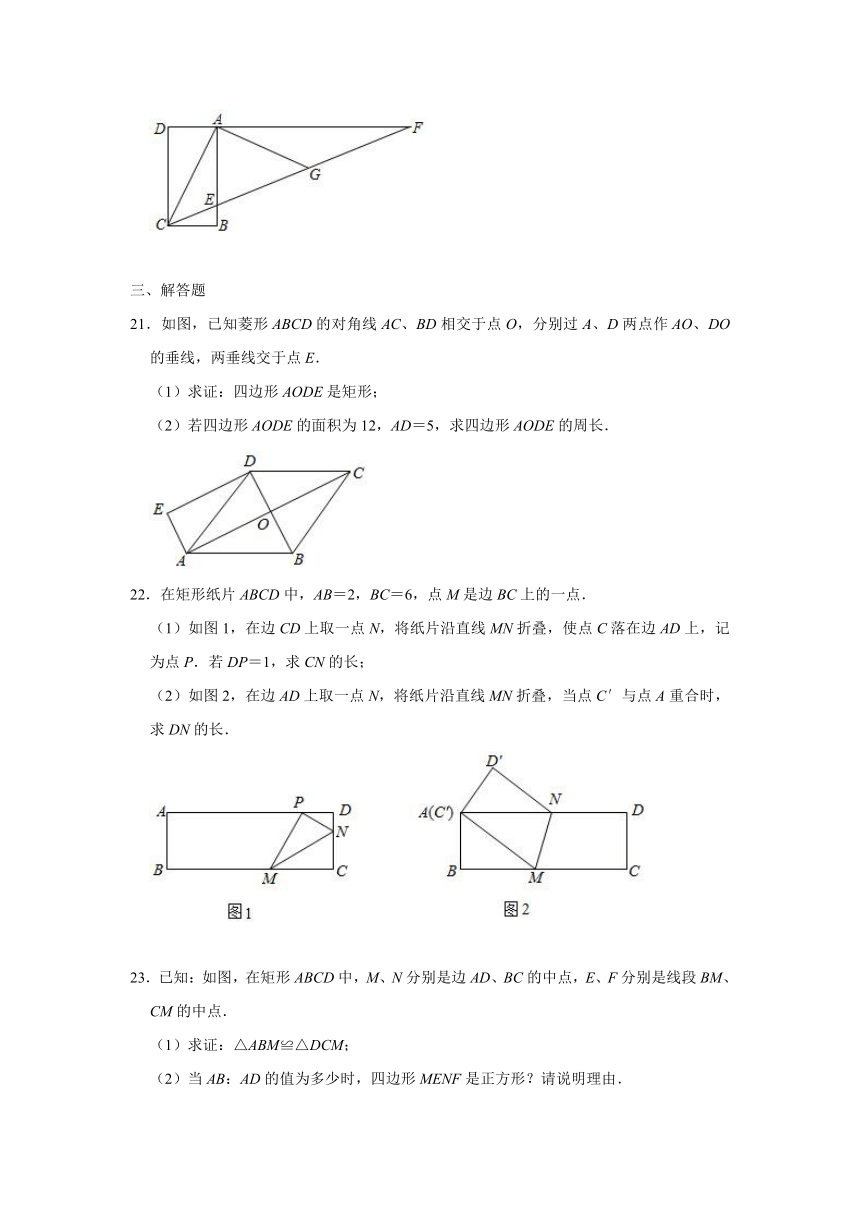
21.如图,已知菱形ABCD的对角线AC、BD相交于点O,分别过A、D两点作AO、DO的垂线,两垂线交于点E.
(1)求证:四边形AODE是矩形;
(2)若四边形AODE的面积为12,AD=5,求四边形AODE的周长.
22.在矩形纸片ABCD中,AB=2,BC=6,点M是边BC上的一点.
(1)如图1,在边CD上取一点N,将纸片沿直线MN折叠,使点C落在边AD上,记为点P.若DP=1,求CN的长;
(2)如图2,在边AD上取一点N,将纸片沿直线MN折叠,当点C′与点A重合时,求DN的长.
23.已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)当AB:AD的值为多少时,四边形MENF是正方形?请说明理由.
24.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.
(1)求证:CE=DE.
(2)当BE=2,CE=1时,求菱形的边长.
25.如图,在平行四边形ABCD中,P是AB上一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q,连接CQ,∠BPC=∠AQP.
(1)求证:四边形ABCD是矩形;
(2)当AP=3,AD=9时,求AQ和CQ的长.
26.如图,过△ABC边AC的中点O,作OE⊥AC,交AB于点E,过点A作AD∥BC,与BO的延长线交于点D,连接CD,CE,若CE平分∠ACB,CE⊥BO于点F.
(1)求证:
①OC=BC;
②四边形ABCD是矩形;
(2)若BC=3,求DE的长.
27.如图,正方形ABCD中,点P是对角线AC上一点,连接PB,边作PE⊥PB交AD边于于点E,且点E不与点A,D重合,作PM⊥AD,PN⊥AB,垂足分别为点M和N.
(1)求证:PM=PN;
(2)求证:EM=BN.
28.如图,已知四边形ABCD为正方形,AB=4,点E为对角线AC上一动点,连接DE、过点E作EF⊥DE.交BC点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
参考答案
1.解:A、有一个角是直角的平行四边形是矩形,此选项错误,不符合题意;
B、对角线互相垂直的矩形是正方形,此选项正确,符合题意;
C、有一组邻边相等的菱形还是菱形,此选项错误,不符合题意;
D、四条边都相等的四边形是菱形,此选项错误,不符合题意.
故选:B.
2.解:①若AB=BC,则?ABCD是菱形,选项说法错误;
②若AC⊥BD,则?ABCD是菱形,选项说法正确;
③若∠ABC=90°,则?ABCD是矩形,选项说法错误;
④若AC=BD,则?ABCD是矩形,选项说法错误;
故选:B.
3.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEO=∠BFO,∠EDO=∠FBO,
∵对角线BD的垂直平分线分别与AD,BC边交于点E、F,
∴BO=DO,EF⊥BD,
∴△DEO≌△BFO(AAS),
∴EO=FO,
∵BO=DO,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF是菱形,
∴BE=DE,
∵AB=5,AD=12,∠A=90°,
∴BD=13,
设DE=x,则AE=12﹣x,
在Rt△AEB中,AB2+AE2=BE2,
即52+(12﹣x)2=x2,
∴x=,
∴BE=DE=,
在Rt△BEO中,OE=,
∴EF=2EO=,
∴菱形BEDF的面积=,
故选:A.
4.解:∵四边形ABCD是矩形,
∴AB=CD=2,∠A=∠D=∠DCB=90°,
∵∠DCE=45°,
∴DE=DC=2,
∴EC=2,
∵∠DCE=45°,
∴∠DEC=45°,
∵EB平分∠AEC,
∴∠AEC=∠AEC=,
∴∠BEC=180°﹣45°﹣67.5°=67.5°,
∴∠AEB=∠BEC,
∴BC=CE=2,
∴AD=BC=2,
∴AE=AD﹣DE=2﹣2,
故选:B.
5.解:∵菱形的对角线互相垂直,但矩形的对角线不一定垂直,
∴菱形具有而矩形不一定具有的是对角线垂直,
故选:B.
6.解:∵四边形ABCD是长方形,
∴∠B=∠C=90°,AB=DC,
∵ED=5,EC=3,
∴DC===4,
则AB=4,
∵AE平分∠BAD交BC于点E,
∴∠BAE=∠DAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠BEA,
∴AB=BE=4,
∴长方形的周长为:2×(4+4+3)=22.
故选:B.
7.解:分两种情况讨论:
①当E点在线段DC上时,
∵△AD'E≌△ADE,
∴∠AD'E=∠D=90°,
∵∠AD'B=90°,
∴∠AD'B+∠AD'E=180°,
∴B、D'、E三点共线,
∵,AD'=AD,
∴BE=AB=10,
∵,
∴DE=D'E=10﹣8=2;
②当E点在线段DC的延长线上时,如下图,
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
∵,
∴△ABD″≌△BEC(ASA),
∴BE=AB=10,
∵,
∴DE=D″E=BD''+BE=8+10=18.
综上所知,DE=2或18.
故选:D.
8.解:∵四边形ABCD是矩形,
∴OA=OB=OD,
∵∠AOD=120°,
∴∠AOB=180°﹣120°=60°,
∴△AOB为等边三角形,
∵AE⊥BD,
∴BE=OE=OB,
∴ED=3BE,
∴=,
故选:A.
9.解:连接CM,如图所示:
∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵ME⊥AC,MF⊥BC,∠ACB=90°,
∴四边形CEMF是矩形,
∴EF=CM,
∵点P是EF的中点,
∴CP=EF,
当CM⊥AB时,CM最短,
此时EF也最小,则CP最小,
∵△ABC的面积=AB×CM=AC×BC,
∴CM===2.4,
∴CP=EF=CM=1.2,
故选:A.
10.解:在正方形ABCD中,OA⊥OB,∠OAD=45°,
∵PE⊥AC,PF⊥BD,
∴四边形OEPF为矩形,△AEP是等腰直角三角形,
∴PF=OE,PE=AE,
∴PE+PF=AE+OE=OA,
∵正方形ABCD的边长为2,
∴OA=AC==.
故选:C.
11.解:如图,过点D作DH⊥AC于H,
∵四边形ABCD是矩形,
∴AC=BD,AO=CO,BO=DO,
∵AB=2,BC=4,
∴AC===2,
∴OD=OC=,
∵S△ADC=×AD×DC=×AC×DH,
∴2×4=2×DH,
∴DH=,
∴OH===,
∴HC=﹣=,
∵CE⊥CA,DH⊥CA,
∴CE∥DH,
∴DE=.
12.解:如图1,当正方形ABDE在AB的右侧时,
∵AB=AC,∠BAC=40°,
∴AC=AE,∠CAE=50°,
∴∠AEC=65°;
如图2,当正方形ABDE在AB的左侧时,
∵AB=AC,∠BAC=40°,
∴AC=AE,∠CAE=130°,
∴∠AEC=25°,
综上所述:∠AEC=25°或65°,
故答案为:25°或65°.
13.解:如图,连接CG并延长,交AD于点M,连接EM,
∵四边形ABCD为菱形,∠B=60°,
∴AD∥BC,
∴∠A=120°,∠MGD=∠CGH,
∵点G为HD的中点,
∴HG=DG,
∵∠MGD=∠CGH,
∴△MGD≌△CGH(ASA),
∴MG=CG,MD=CH=BC=AD,
∴点G为MC的中点,点M为AD的中点,
∵F,G分别为CE和CM的中点,
∴FG是△CEM的中位线,
∴FG=EM,
∴EM=2FG=4,
∵E,M分别为AB和AD的中点,
∴AE=AM,
∵∠A=120°,
∴EM=AE=4,
∴AE=4,
∴AB=2AE=8.
故答案为:8.
14.解:如图,延长CF,BA交于点G,连接EF,过点F作FH⊥CE于H,过点E作EM⊥CF于M,
∵四边形ABCD是矩形,且AB=,BC=4,
∴AB∥CD,AB=CD=,∠D=∠ABC=∠CBE=90°,
∴∠DCF=∠G,
∵CF平分∠ECD,
∴∠DCF=∠FCE,FH=DF,
∴∠G=∠ECF,
∴EC=EG,
∴∠ECG是等腰三角形,
∴CM=MG,
∵CE=CF,
∴△ECF是等腰三角形,
∵EM⊥CF,FH⊥CE,
∴EM和FH是等腰三角形腰上的高,
∴EM=FH=DF,
∴Rt△CDF≌Rt△CME(HL),
∴CM=CD=,
∴CG=5,
Rt△CBG中,BG===3,
设BE=x,则EC=EG=3+x,
Rt△CBE中,(3+x)2=x2+42,
解得:x=,
∴BE=.
故答案为:.
15.解:∵四边形ABCD是正方形,
∴∠ACB=45°,AD∥BC,
∵AC=EC,
∴∠E=∠CAE,
∵∠ACB=∠E+∠CAE=2∠E,
∴∠E=∠ACB=22.5°,
∵AD∥BC,
∴∠DAE=∠E=22.5°.
故答案为:22.5°.
16.解:连接BP,如图,由题意可知BP为Rt△BEF的斜边中线,
∵EF=4m,
∴BP=2m,
∵AB=DC=4m,BC=AD=6m,
∴点P的运动轨迹为四个圆心分别在点A,B,C,D,半径为2m的四分之一圆,以及BC和AD上的一段线段.
长为6m,宽为4m的矩形花池ABCD的面积为6×4=24(m2).
∴种植年花的区域的面积是:24﹣π×22=(24﹣4π)(m2).
故答案为:(24﹣4π).
17.解:在Rt△AEB中,∠AEB=90°,AE=5,BE=12,
由勾股定理得:AB==13,
∴正方形的面积是13×13=169,
∵△AEB的面积是AE×BE=×5×12=30,
∴阴影部分的面积是169﹣30=139,
故答案为:139.
18.解:∵四边形ABCD是正方形,
∴AD=DC,∠ADC=∠C=90°.
在△ADE和△DCF中,
,
∴△ADE≌△DCF(SAS).
∴AE=DF,∠DAE=∠CDF,
∵∠CDF+∠ADF=90°,
∴∠DAE+∠ADF=90°.
∴AE⊥DF,
∴点P的路径是一段以AD为直径的弧,
如图,
设AD的中点为Q,连接QC交弧于点P,此时CP的长度最小,
在Rt△QDC中,QC===2,
∴CP=QC﹣QP=2﹣2,
故答案为2﹣2.
19.解:在Rt△ABC中,点D是斜边AB的中点,CD=2,
∴AB=2CD=2×2=4,
故答案为:4.
20.解:∵四边形ABCD是矩形,
∴AD∥BC,∠DCB=90°,
∴∠F=∠ECB=20°,
∴∠GAF=∠F=20°,
∴∠ACG=∠AGC=∠GAF+∠F=2∠F=40°,
∴∠ACB=∠ACG+∠ECB=60°,
∴∠ACD=90°﹣60°=30°,
故答案为:30°.
21.(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=90°,
∵EA⊥AO,DE⊥DO,
∴∠EAO=∠DOA=90°,
∴四边形AODE是矩形;
(2)解:由(1)知,四边形AODE是矩形,
∴∠AED=90°,OA=DE,OD=AE,
∵四边形AODE的面积为12,
∴OA?OD=12,
在Rt△AOD中,根据勾股定理,得OA2+OD2=AD2=25,
∴(OA+OD)2=OA2+2OA?OD+OD2=25+24=49,
∴OA+OD=7,
∴四边形AODE的周长为2(OA+OD)=14.
22.解:(1)矩形ABCD中,AB=DC=2,AD=BC=6,∠BAC=∠ABC=∠BCD=∠CDA=90°,
设CN=x,则DN=CD﹣CN=2﹣x,
由折叠可得,PN=CN=x,
在Rt△PDN中,DP2+DN2=PN2,
即12+(2﹣x)2=x2,
解得:x=,
∴CN=;
(2)当点C'与点A重合时,
设DN=y,则AN=AD﹣DN=6﹣y,
由折叠可得,D'N=DN=y,AD'=CD=2,∠AD'N=∠CDA=90°,
在Rt△AD'N中,AD'2+D'N2=AN2,
即22+y2=(6﹣y)2,
解得:y=,
∴DN=.
23.(1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠A=∠D=90°,
∵M为AD中点,
∴AM=DM,
在△ABM和△DCM,
,
∴△ABM≌△DCM(SAS);
(2)解:当AB:AD=1:2时,四边形MENF是正方形,
理由:当四边形MENF是正方形时,则∠EMF=90°,
∵△ABM≌△DCM,
∴∠AMB=∠DMC=45°,
∴△ABM、△DCM为等腰直角三角形,
∴AM=DM=AB,
∴AD=2AB,
即当AB:AD=1:2时,四边形MENF是正方形.
24.(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=CB,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,
∵AE=DE,
∴CE=DE;
(2)解:如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AH⊥BD,BH=DH,AH=CH,
∵CE=DE=AE=1,
∴BD=BE+DE=2+1=3,
∴BH=BD=,EH=BE﹣BH=2﹣=,
在Rt△AHE中,由勾股定理得:AH===,
在Rt△AHB中,由勾股定理得:AB===,
∴菱形的边长为.
25.(1)证明:∵∠BPQ=∠BPC+∠CPQ=∠A+∠AQP,∠BPC=∠AQP,
∴∠CPQ=∠A,
∵PQ⊥CP,
∴∠A=∠CPQ=90°,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴∠D=∠CPQ=90°,
在Rt△CDQ和Rt△CPQ中,
,
∴Rt△CDQ≌Rt△CPQ(HL),
∴DQ=PQ,
设AQ=x,则DQ=PQ=12﹣x,
在Rt△APQ中,AQ2+AP2=PQ2,
∴x2+32=(9﹣x)2,
解得:x=4,
∴AQ的长是4.
设CD=AB=CP=y,则PB=y﹣3,在Rt△PCB中,根据勾股定理列方程,求出y=15.
在Rt△CDQ中,CQ==5.
26.(1)证明:①∵CE平分∠ACB,
∴∠OCE=∠BCE,
∵BO⊥CE,
∴∠CFO=∠CFB=90°,
在△OCF与△BCF中,
,
∴△OCF≌△BCF(ASA),
∴OC=BC;
②∵点O是AC的中点,
∴OA=OC,
∵AD∥BC,
∴∠DAO=∠BCO,∠ADO=∠CBO,
在△OAD与△OCB中,
,
∴△OAD≌△OCB(ASA),
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵OE⊥AC,
∴∠EOC=90°,
在△OCE与△BCE中,
,
∴△OCE≌△BCE(SAS),
∴∠EBC=∠EOC=90°,
∴四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴AD=BC=3,∠DAB=90°,AC=BD,
∴OB=OC,
∵OC=BC,
∴OC=OB=BC,
∴△OBC是等边三角形,
∴∠OCB=60°,
∴∠ECB=OCB=30°,
∵∠EBC=90°,
∴EB=EC,
∵BE2+BC2=EC2,BC=3,
∴EB=,EC=2,
∵OE⊥AC,OA=OC,
∴EC=EA=2,
在Rt△ADE中,∠DAB=90°,
∴DE===.
27.证明:(1)∵四边形ABCD为正方形,
∴AC平分∠BAD,
又∵PM⊥AD,PN⊥AB,
∴PM=PN.
(2)∵PM⊥AD,PN⊥AB,∠MAN=90°,PM=PN,
∴四边形PMAN为正方形,
∴∠MPN=90°,即∠MPE+∠EPN=90°.
∵PE⊥PB,
∴∠EPN+∠NPB=90°,
∴∠MPE=∠NPB.
∵PM⊥AD,PN⊥AB,
∴∠PME=∠PNB=90°.
在△PME和△PNB中,,
∴△PME≌△PNB(ASA),
∴EM=BN.
28.解:(1)如图所示,过E作EM⊥BC于M点,过E作EN⊥CD于N点,
∵正方形ABCD,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°,且NE=NC,
∴四边形EMCN为正方形,
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
(2)CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°,
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴AC=AE+CE=AB=×4=8,
∴CE+CG=8是定值.
一、选择题
1.下列说法正确的是 )
A.有一个角是直角的平行四边形是正方形 B.对角线互相垂直的矩形是正方形
C.有一组邻边相等的菱形是正方形 D.各边都相等的四边形是正方形
2.已知四边形ABCD是平行四边形,下列说法正确的有( )
①当AB=BC时,它是矩形②AC⊥BD时,它是菱形
③当∠ABC=90°时,它是菱形④当AC=BD时,它是正方形
A.①② B.② C.②④ D.③④
3.如图,在矩形ABCD中,AB=5,AD=12,对角线BD的垂直平分线分别与AD,BC边交于点E、F,则四边形BFDE的面积为( )
A. B. C. D.
4.如图,矩形ABCD中,AB=2,点E在边AD上,EB平分∠AEC,∠DCE=45°,则AE长( )
A. B.2﹣2 C.2﹣ D.2
5.下列性质中,菱形具有而矩形不一定具有的是( )
A.对角线相等 B.对角线垂直 C.邻边垂直 D.邻角互补
6.如图,在长方形ABCD中,AE平分∠BAD交BC于点E,连接ED,若ED=5,EC=3,则长方形的周长为( )
A.20 B.22 C.24 D.26
7.如图,长方形ABCD中,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为( )
A.2或8 B.或18 C.或2 D.2或18
8.如图,矩形ABCD的对角线AC,BD相交于点O,且∠AOD=120°.过点A作AE⊥BD于点E,则BE:ED等于( )
A.1:3 B.1:4 C.2:3 D.2:5
9.如图,在直角三角形ABC中,∠ACB=90°,AC=3,BC=4,点M是边AB上一点(不与点A,B重合),作ME⊥AC于点E,MF⊥BC于点F,若点P是EF的中点,则CP的最小值是( )
A.1.2 B.1.5 C.2.4 D.2.5
10.如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.4 B.2 C. D.2
二、填空题
11.如图,在矩形ABCD中,对角线AC,BD交于点O,过点C作CE⊥CA,交BD的延长线于点E,若AB=2,BC=4,则DE的长为 .
12.如图,在△ABC中,AB=AC,∠BAC=40°,以AB为边作正方形ABDE,连接CE,则∠AEC= .
13.如图,在菱形ABCD中,∠B=60°,E,H分别为AB,BC的中点,G,F分别为线段HD,CE的中点.若线段FG的长为2?,则AB的长为 .
14.在长方形ABCD中,AB=,BC=4,CE=CF,延长AB至点E,连接CE,CF平分∠ECD,则BE= .
15.如图,四边形ABCD是一个正方形,E是BC延长线上的一点,且AC=EC,则∠DAE= .
16.为了迎接2021年春节,李师傅计划改造一个长为6m,宽为4m的矩形花池ABCD,如图,他将画线工具固定在一根4m木棍EF的中点P处.画线时,使点E,F都在花池边的轨道上按逆时针方向滑动一周.若将点P所画出的封闭图形围成的区域全部种植年花,则种植年花的区域的面积是 m2.
17.如图,四边形ABCD是正方形,AE⊥BE于点E,且AE=5,BE=12,则阴影部分的面积是 .
18.如图,在边长为4的正方形ABCD中,动点E,F分别在CD,BC上移动,CF=DE,AE和DF交于点P,则线段CP的最小值是 .
19.Rt△ABC中,∠C=90°,点D是斜边AB的中点,若CD=2,则AB= .
20.如图,四边形ABCD是长方形,F是DA延长线上一点,CF交AB于点E,G是CF上一点,且∠ACG=∠AGC,∠GAF=∠F.若∠ECB=20°,则∠ACD的度数是 .
三、解答题
21.如图,已知菱形ABCD的对角线AC、BD相交于点O,分别过A、D两点作AO、DO的垂线,两垂线交于点E.
(1)求证:四边形AODE是矩形;
(2)若四边形AODE的面积为12,AD=5,求四边形AODE的周长.
22.在矩形纸片ABCD中,AB=2,BC=6,点M是边BC上的一点.
(1)如图1,在边CD上取一点N,将纸片沿直线MN折叠,使点C落在边AD上,记为点P.若DP=1,求CN的长;
(2)如图2,在边AD上取一点N,将纸片沿直线MN折叠,当点C′与点A重合时,求DN的长.
23.已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)当AB:AD的值为多少时,四边形MENF是正方形?请说明理由.
24.如图,在菱形ABCD中,E为对角线BD上一点,且AE=DE,连接CE.
(1)求证:CE=DE.
(2)当BE=2,CE=1时,求菱形的边长.
25.如图,在平行四边形ABCD中,P是AB上一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q,连接CQ,∠BPC=∠AQP.
(1)求证:四边形ABCD是矩形;
(2)当AP=3,AD=9时,求AQ和CQ的长.
26.如图,过△ABC边AC的中点O,作OE⊥AC,交AB于点E,过点A作AD∥BC,与BO的延长线交于点D,连接CD,CE,若CE平分∠ACB,CE⊥BO于点F.
(1)求证:
①OC=BC;
②四边形ABCD是矩形;
(2)若BC=3,求DE的长.
27.如图,正方形ABCD中,点P是对角线AC上一点,连接PB,边作PE⊥PB交AD边于于点E,且点E不与点A,D重合,作PM⊥AD,PN⊥AB,垂足分别为点M和N.
(1)求证:PM=PN;
(2)求证:EM=BN.
28.如图,已知四边形ABCD为正方形,AB=4,点E为对角线AC上一动点,连接DE、过点E作EF⊥DE.交BC点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
参考答案
1.解:A、有一个角是直角的平行四边形是矩形,此选项错误,不符合题意;
B、对角线互相垂直的矩形是正方形,此选项正确,符合题意;
C、有一组邻边相等的菱形还是菱形,此选项错误,不符合题意;
D、四条边都相等的四边形是菱形,此选项错误,不符合题意.
故选:B.
2.解:①若AB=BC,则?ABCD是菱形,选项说法错误;
②若AC⊥BD,则?ABCD是菱形,选项说法正确;
③若∠ABC=90°,则?ABCD是矩形,选项说法错误;
④若AC=BD,则?ABCD是矩形,选项说法错误;
故选:B.
3.解:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEO=∠BFO,∠EDO=∠FBO,
∵对角线BD的垂直平分线分别与AD,BC边交于点E、F,
∴BO=DO,EF⊥BD,
∴△DEO≌△BFO(AAS),
∴EO=FO,
∵BO=DO,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴平行四边形BEDF是菱形,
∴BE=DE,
∵AB=5,AD=12,∠A=90°,
∴BD=13,
设DE=x,则AE=12﹣x,
在Rt△AEB中,AB2+AE2=BE2,
即52+(12﹣x)2=x2,
∴x=,
∴BE=DE=,
在Rt△BEO中,OE=,
∴EF=2EO=,
∴菱形BEDF的面积=,
故选:A.
4.解:∵四边形ABCD是矩形,
∴AB=CD=2,∠A=∠D=∠DCB=90°,
∵∠DCE=45°,
∴DE=DC=2,
∴EC=2,
∵∠DCE=45°,
∴∠DEC=45°,
∵EB平分∠AEC,
∴∠AEC=∠AEC=,
∴∠BEC=180°﹣45°﹣67.5°=67.5°,
∴∠AEB=∠BEC,
∴BC=CE=2,
∴AD=BC=2,
∴AE=AD﹣DE=2﹣2,
故选:B.
5.解:∵菱形的对角线互相垂直,但矩形的对角线不一定垂直,
∴菱形具有而矩形不一定具有的是对角线垂直,
故选:B.
6.解:∵四边形ABCD是长方形,
∴∠B=∠C=90°,AB=DC,
∵ED=5,EC=3,
∴DC===4,
则AB=4,
∵AE平分∠BAD交BC于点E,
∴∠BAE=∠DAE,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠BEA,
∴AB=BE=4,
∴长方形的周长为:2×(4+4+3)=22.
故选:B.
7.解:分两种情况讨论:
①当E点在线段DC上时,
∵△AD'E≌△ADE,
∴∠AD'E=∠D=90°,
∵∠AD'B=90°,
∴∠AD'B+∠AD'E=180°,
∴B、D'、E三点共线,
∵,AD'=AD,
∴BE=AB=10,
∵,
∴DE=D'E=10﹣8=2;
②当E点在线段DC的延长线上时,如下图,
∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,
∴∠CBE=∠BAD″,
在△ABD″和△BEC中,
∵,
∴△ABD″≌△BEC(ASA),
∴BE=AB=10,
∵,
∴DE=D″E=BD''+BE=8+10=18.
综上所知,DE=2或18.
故选:D.
8.解:∵四边形ABCD是矩形,
∴OA=OB=OD,
∵∠AOD=120°,
∴∠AOB=180°﹣120°=60°,
∴△AOB为等边三角形,
∵AE⊥BD,
∴BE=OE=OB,
∴ED=3BE,
∴=,
故选:A.
9.解:连接CM,如图所示:
∵∠ACB=90°,AC=3,BC=4,
∴AB===5,
∵ME⊥AC,MF⊥BC,∠ACB=90°,
∴四边形CEMF是矩形,
∴EF=CM,
∵点P是EF的中点,
∴CP=EF,
当CM⊥AB时,CM最短,
此时EF也最小,则CP最小,
∵△ABC的面积=AB×CM=AC×BC,
∴CM===2.4,
∴CP=EF=CM=1.2,
故选:A.
10.解:在正方形ABCD中,OA⊥OB,∠OAD=45°,
∵PE⊥AC,PF⊥BD,
∴四边形OEPF为矩形,△AEP是等腰直角三角形,
∴PF=OE,PE=AE,
∴PE+PF=AE+OE=OA,
∵正方形ABCD的边长为2,
∴OA=AC==.
故选:C.
11.解:如图,过点D作DH⊥AC于H,
∵四边形ABCD是矩形,
∴AC=BD,AO=CO,BO=DO,
∵AB=2,BC=4,
∴AC===2,
∴OD=OC=,
∵S△ADC=×AD×DC=×AC×DH,
∴2×4=2×DH,
∴DH=,
∴OH===,
∴HC=﹣=,
∵CE⊥CA,DH⊥CA,
∴CE∥DH,
∴DE=.
12.解:如图1,当正方形ABDE在AB的右侧时,
∵AB=AC,∠BAC=40°,
∴AC=AE,∠CAE=50°,
∴∠AEC=65°;
如图2,当正方形ABDE在AB的左侧时,
∵AB=AC,∠BAC=40°,
∴AC=AE,∠CAE=130°,
∴∠AEC=25°,
综上所述:∠AEC=25°或65°,
故答案为:25°或65°.
13.解:如图,连接CG并延长,交AD于点M,连接EM,
∵四边形ABCD为菱形,∠B=60°,
∴AD∥BC,
∴∠A=120°,∠MGD=∠CGH,
∵点G为HD的中点,
∴HG=DG,
∵∠MGD=∠CGH,
∴△MGD≌△CGH(ASA),
∴MG=CG,MD=CH=BC=AD,
∴点G为MC的中点,点M为AD的中点,
∵F,G分别为CE和CM的中点,
∴FG是△CEM的中位线,
∴FG=EM,
∴EM=2FG=4,
∵E,M分别为AB和AD的中点,
∴AE=AM,
∵∠A=120°,
∴EM=AE=4,
∴AE=4,
∴AB=2AE=8.
故答案为:8.
14.解:如图,延长CF,BA交于点G,连接EF,过点F作FH⊥CE于H,过点E作EM⊥CF于M,
∵四边形ABCD是矩形,且AB=,BC=4,
∴AB∥CD,AB=CD=,∠D=∠ABC=∠CBE=90°,
∴∠DCF=∠G,
∵CF平分∠ECD,
∴∠DCF=∠FCE,FH=DF,
∴∠G=∠ECF,
∴EC=EG,
∴∠ECG是等腰三角形,
∴CM=MG,
∵CE=CF,
∴△ECF是等腰三角形,
∵EM⊥CF,FH⊥CE,
∴EM和FH是等腰三角形腰上的高,
∴EM=FH=DF,
∴Rt△CDF≌Rt△CME(HL),
∴CM=CD=,
∴CG=5,
Rt△CBG中,BG===3,
设BE=x,则EC=EG=3+x,
Rt△CBE中,(3+x)2=x2+42,
解得:x=,
∴BE=.
故答案为:.
15.解:∵四边形ABCD是正方形,
∴∠ACB=45°,AD∥BC,
∵AC=EC,
∴∠E=∠CAE,
∵∠ACB=∠E+∠CAE=2∠E,
∴∠E=∠ACB=22.5°,
∵AD∥BC,
∴∠DAE=∠E=22.5°.
故答案为:22.5°.
16.解:连接BP,如图,由题意可知BP为Rt△BEF的斜边中线,
∵EF=4m,
∴BP=2m,
∵AB=DC=4m,BC=AD=6m,
∴点P的运动轨迹为四个圆心分别在点A,B,C,D,半径为2m的四分之一圆,以及BC和AD上的一段线段.
长为6m,宽为4m的矩形花池ABCD的面积为6×4=24(m2).
∴种植年花的区域的面积是:24﹣π×22=(24﹣4π)(m2).
故答案为:(24﹣4π).
17.解:在Rt△AEB中,∠AEB=90°,AE=5,BE=12,
由勾股定理得:AB==13,
∴正方形的面积是13×13=169,
∵△AEB的面积是AE×BE=×5×12=30,
∴阴影部分的面积是169﹣30=139,
故答案为:139.
18.解:∵四边形ABCD是正方形,
∴AD=DC,∠ADC=∠C=90°.
在△ADE和△DCF中,
,
∴△ADE≌△DCF(SAS).
∴AE=DF,∠DAE=∠CDF,
∵∠CDF+∠ADF=90°,
∴∠DAE+∠ADF=90°.
∴AE⊥DF,
∴点P的路径是一段以AD为直径的弧,
如图,
设AD的中点为Q,连接QC交弧于点P,此时CP的长度最小,
在Rt△QDC中,QC===2,
∴CP=QC﹣QP=2﹣2,
故答案为2﹣2.
19.解:在Rt△ABC中,点D是斜边AB的中点,CD=2,
∴AB=2CD=2×2=4,
故答案为:4.
20.解:∵四边形ABCD是矩形,
∴AD∥BC,∠DCB=90°,
∴∠F=∠ECB=20°,
∴∠GAF=∠F=20°,
∴∠ACG=∠AGC=∠GAF+∠F=2∠F=40°,
∴∠ACB=∠ACG+∠ECB=60°,
∴∠ACD=90°﹣60°=30°,
故答案为:30°.
21.(1)证明:∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOD=90°,
∵EA⊥AO,DE⊥DO,
∴∠EAO=∠DOA=90°,
∴四边形AODE是矩形;
(2)解:由(1)知,四边形AODE是矩形,
∴∠AED=90°,OA=DE,OD=AE,
∵四边形AODE的面积为12,
∴OA?OD=12,
在Rt△AOD中,根据勾股定理,得OA2+OD2=AD2=25,
∴(OA+OD)2=OA2+2OA?OD+OD2=25+24=49,
∴OA+OD=7,
∴四边形AODE的周长为2(OA+OD)=14.
22.解:(1)矩形ABCD中,AB=DC=2,AD=BC=6,∠BAC=∠ABC=∠BCD=∠CDA=90°,
设CN=x,则DN=CD﹣CN=2﹣x,
由折叠可得,PN=CN=x,
在Rt△PDN中,DP2+DN2=PN2,
即12+(2﹣x)2=x2,
解得:x=,
∴CN=;
(2)当点C'与点A重合时,
设DN=y,则AN=AD﹣DN=6﹣y,
由折叠可得,D'N=DN=y,AD'=CD=2,∠AD'N=∠CDA=90°,
在Rt△AD'N中,AD'2+D'N2=AN2,
即22+y2=(6﹣y)2,
解得:y=,
∴DN=.
23.(1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠A=∠D=90°,
∵M为AD中点,
∴AM=DM,
在△ABM和△DCM,
,
∴△ABM≌△DCM(SAS);
(2)解:当AB:AD=1:2时,四边形MENF是正方形,
理由:当四边形MENF是正方形时,则∠EMF=90°,
∵△ABM≌△DCM,
∴∠AMB=∠DMC=45°,
∴△ABM、△DCM为等腰直角三角形,
∴AM=DM=AB,
∴AD=2AB,
即当AB:AD=1:2时,四边形MENF是正方形.
24.(1)证明:∵四边形ABCD是菱形,
∴∠ABE=∠CBE,AB=CB,
在△ABE和△CBE中,
,
∴△ABE≌△CBE(SAS),
∴AE=CE,
∵AE=DE,
∴CE=DE;
(2)解:如图,连接AC交BD于H,
∵四边形ABCD是菱形,
∴AH⊥BD,BH=DH,AH=CH,
∵CE=DE=AE=1,
∴BD=BE+DE=2+1=3,
∴BH=BD=,EH=BE﹣BH=2﹣=,
在Rt△AHE中,由勾股定理得:AH===,
在Rt△AHB中,由勾股定理得:AB===,
∴菱形的边长为.
25.(1)证明:∵∠BPQ=∠BPC+∠CPQ=∠A+∠AQP,∠BPC=∠AQP,
∴∠CPQ=∠A,
∵PQ⊥CP,
∴∠A=∠CPQ=90°,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴∠D=∠CPQ=90°,
在Rt△CDQ和Rt△CPQ中,
,
∴Rt△CDQ≌Rt△CPQ(HL),
∴DQ=PQ,
设AQ=x,则DQ=PQ=12﹣x,
在Rt△APQ中,AQ2+AP2=PQ2,
∴x2+32=(9﹣x)2,
解得:x=4,
∴AQ的长是4.
设CD=AB=CP=y,则PB=y﹣3,在Rt△PCB中,根据勾股定理列方程,求出y=15.
在Rt△CDQ中,CQ==5.
26.(1)证明:①∵CE平分∠ACB,
∴∠OCE=∠BCE,
∵BO⊥CE,
∴∠CFO=∠CFB=90°,
在△OCF与△BCF中,
,
∴△OCF≌△BCF(ASA),
∴OC=BC;
②∵点O是AC的中点,
∴OA=OC,
∵AD∥BC,
∴∠DAO=∠BCO,∠ADO=∠CBO,
在△OAD与△OCB中,
,
∴△OAD≌△OCB(ASA),
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵OE⊥AC,
∴∠EOC=90°,
在△OCE与△BCE中,
,
∴△OCE≌△BCE(SAS),
∴∠EBC=∠EOC=90°,
∴四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴AD=BC=3,∠DAB=90°,AC=BD,
∴OB=OC,
∵OC=BC,
∴OC=OB=BC,
∴△OBC是等边三角形,
∴∠OCB=60°,
∴∠ECB=OCB=30°,
∵∠EBC=90°,
∴EB=EC,
∵BE2+BC2=EC2,BC=3,
∴EB=,EC=2,
∵OE⊥AC,OA=OC,
∴EC=EA=2,
在Rt△ADE中,∠DAB=90°,
∴DE===.
27.证明:(1)∵四边形ABCD为正方形,
∴AC平分∠BAD,
又∵PM⊥AD,PN⊥AB,
∴PM=PN.
(2)∵PM⊥AD,PN⊥AB,∠MAN=90°,PM=PN,
∴四边形PMAN为正方形,
∴∠MPN=90°,即∠MPE+∠EPN=90°.
∵PE⊥PB,
∴∠EPN+∠NPB=90°,
∴∠MPE=∠NPB.
∵PM⊥AD,PN⊥AB,
∴∠PME=∠PNB=90°.
在△PME和△PNB中,,
∴△PME≌△PNB(ASA),
∴EM=BN.
28.解:(1)如图所示,过E作EM⊥BC于M点,过E作EN⊥CD于N点,
∵正方形ABCD,
∴∠BCD=90°,∠ECN=45°,
∴∠EMC=∠ENC=∠BCD=90°,且NE=NC,
∴四边形EMCN为正方形,
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°,
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
(2)CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°,
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°,
∴∠ADE=∠CDG,
在△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴AC=AE+CE=AB=×4=8,
∴CE+CG=8是定值.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
