19.1.2.2函数的三种表示方法 课件(共38张PPT)
文档属性
| 名称 | 19.1.2.2函数的三种表示方法 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-06 00:00:00 | ||
图片预览











文档简介
19.1.2.2 函数的三种表示方法
第十九章 一次函数
2021年春人教版八年级(下)数学
上节课我们学习了函数图象的意义和画函数图象的方法,这节课我们结合实例来总结画函数图象的一般步骤.
新课导入
(1)能用描点法画函数的图象.
(2)能从函数图象上看出函数与自变量的变化规律.
(3)知道函数的三种表示方法及它们的优缺点.
重点:用描点法画函数的图象,从函数图象上读取信息.
难点:从图象中说明函数的增减情况.
学习目标
定义:用解析式来表示函数关系的方法叫做解析式法.
解析式法
我们之前是怎么求函数解析式的?
想
想
一
探究新知
例1 汽车油箱中有汽油50L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,耗油量为0.1L/km.写出表示y与x的函数关系的式子.
分析:行驶路程x是自变量,邮箱中的油量y是x的函数,汽车的耗油量为0.1L/km,则x与y的关系为:
y=50-0.1x
例题讲解
考虑到x代表的实际意义为行驶路程,因此x不能取负数.而且行驶中的耗油量不能超过总的油量,所以有:
50-0.1x≥0
x≤500
0≤ x≤500
自变量的取值范围为:
完整的函数解析式为:
y=50-0.1x(0≤ x≤500)
例题讲解
思
考
用解析式法表示函数有什么优缺点?
解析式法简单明了,能够准确的反映整个变化过程中自变量与函数之间的对应关系,但有些实际问题中的函数关系,不能用解析式表示,如气温与时间的函数关系.
探究新知
用解析式法表示函数时需要注意什么?
1.函数解析式是一个等式;
2.是用含自变量的式子表示函数;
3.要确定自变量的取值范围.
探究新知
列表法
定义:用表格来表示函数关系的方法叫做列表法.
例2 在下列式子中,对于x的每一个确定的值,y都有唯一的对应值,即y是x的函数.从x的取值范围中选取一些数值,算出y的对应值,列表.
探究新知
(1)y=x+0.5
分析:从式子y=x+0.5可以看出,x取任意实数时这个式子都有意义,所以x的取值范围是全体实数.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
…
-3
-2
-1
0
1
2
3
…
y
…
-0.5
0.5
1.5
2.5
…
-2.5
-1.5
3.5
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
…
0.5
1
1.5
2
2.5
3
3.5
4
5
6
…
y
…
6
3
2
1.5
…
12
4
2.4
1.2
1
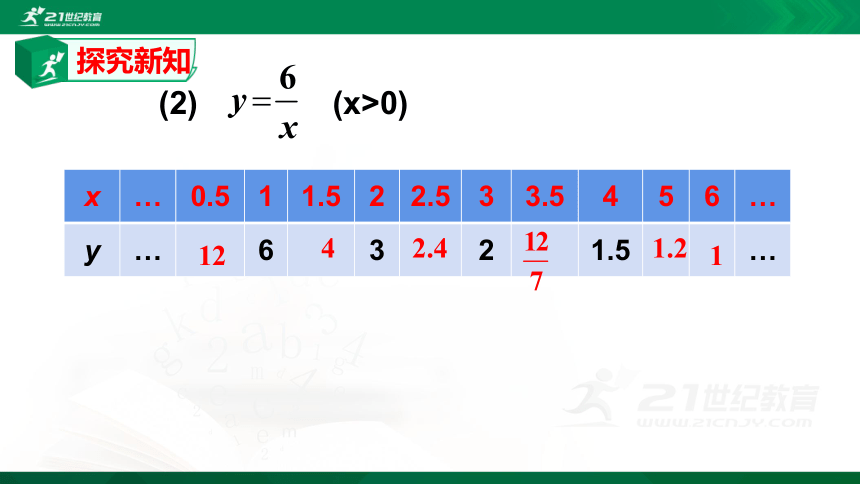
(2) (x>0)
探究新知
思
考
用列表法表示函数有什么优缺点?
列表法一目了然,使用起来比较方便,但列出的对应值是有限的,不易看出自变量与函数之间的对应规律.
探究新知
用列表法与解析式法表示n边形的内角和和m(单位:度)关于边数n的函数.
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}边数n
3
4
5
6
7
…
内角和度数m
180
360
540
720
900
…
思路分析:绘制表格,从表格中得到内角和与边数的变化规律,再写出函数关系式.
针对练习
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}边数n
3
4
5
6
7
…
内角和度数m
180
360
540
720
900
…
边数增加1,内角和度数增加180°,所以n边形的内角和:m=180(n-2).
也就是说多边形的边数增加1,它的内角和就会增加180° .
针对练习
图象法
定义:用图象来表示函数关系的方法叫做图象法.
根据例2列出的表格,画出相应的函数图象.
探究新知
-2
(1)y=x+0.5
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
…
-3
-2
-1
0
1
2
3
…
y
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
从函数图象可以看出,直线从左到右上升,即当x由小变大时,y=x+0.5随之增大.
O
x
y
1
1
-1
-1
y=x+0.5
2
2
-2
(2) (x>0)
从函数图象可以看出,曲线从左向右下降,即当x由小变大时,
随之减小.
(x>0)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
…
0.5
1
1.5
2
2.5
3
3.5
4
5
6
…
y
…
6
3
2
1.5
…
12
4
2.4
1.2
1
O
x
y
6
2
1
3
4
5
1
2
3
4
5
6
(x>0)
思
考
用图象法表示函数有什么优缺点?
图象法形象直观,但只能近似的表达两个变量之间的函数关系.
1.用解析式法与图象法表示等边三角形的周长l关于边长a的函数.
解析式法:
等边三角形周长l=3a (a>0).
针对练习
函数l=3a??(a>0)的图象是过点O的射线(不含端点).图象又过点(1,3),故只要过点O和(1,3)作射线即可.(端点为虚点)
图象法:(如图所示)
2.一条小船沿直线向码头匀速前进.在0min,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.小船与码头的距离s是时间t的函数吗?如果是,写出函数解析式,并画出函数图象.如果船速不变,多长时间后小船到达码头?
解析:用表格列出s与t的对应关系,如下表
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
2
4
6
s
200
150
100
50
观察上表可得出x与s的关系式为:
s=200-25x(0≤x≤8)
所以小船与码头的距离s是时间t的函数.
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}t
0
2
4
6
s
200
150
100
50
画函数图象
O
s(m)
t(min)
50
2
100
150
200
4
6
8
由图象可知,在第8min时,小船与码头的距离为0,即船速不变时,8min后小船到达码头.
思
考
表示函数时,能不能只用一种方法?还是要结合同时使用几种方法?
例3 一个水库的水位在最近5h内持续上涨.下表记录了这5h内6个时间点的水位高度,其中t表示时间,y表示水位高度.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t/h
0
1
2
3
4
5
y/m
3
3.3
3.6
3.9
4.2
4.5
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律吗?
例题讲解
下图所描出的是表中数据对应的点.
这些点在一条直线上.
水位越来越高.
水位高度y是否为时间t的函数?如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.这个函数能表示水位的变化规律吗?
y=0.3t+3(0≤t≤5)
能
(3)据估计这种上涨情况还会持续2h,预测再过2h水位高度将达到多少米?
再过2小时的水位高度,就是t=5+2=7时,
y=0.3t+3的函数值,
故有y=0.3×7+3=5.1(m),
也可利用函数图象估计出这个值.
归
纳
表示函数时,要根据具体情况选择适当的方法,有时为了全面的认识问题,需要同时使用几种方法.
1.向最大容量为60升的热水器内注水,每分钟注水10升,注水2分钟后停止注水1分钟,然后继续注水,直至注满.则能反映注水量与注水时间之间的函数关系的图象是( )
D
A
B
C
D
课堂练习
2.星期日上午9时小王从家中出发到距家900米处的书店买书,如图是9时~10时这段时间内他与家的距离随时间变化的图象.根据此图象,请你用简短的语句分别叙述小王在9时10分至9时15分与9时30分至9时50分这两段时间内活动的情况:
9时10分至9时15分: ;
9时30分至9时50分: .
在家
在书店买书
3.用描点法画出函数y=x+2的图象.
解:列表
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
-2
-1
0
1
2
y
0
1
2
3
4
、描点、连线后得到的图象如图所示.
4.用描点法画出函数y=-6x的图象.
解:列表
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
-1
-?
0
?
1
y
6
3
0
-3
-6
并描点、连线后得到的图象如图所示.
5.弹簧的长度与所挂物体的质量的关系如图所示,观察图象回答:
(1)弹簧没挂物体的长度是多少?
解:当x=0时,y=10,即弹簧没挂物体的长度是10 cm.
(2)弹簧所挂物体的最大质量是多少?这时弹簧的长度是多少?
弹簧所挂物体的最大质量是20kg;
这时弹簧的长度为20cm.
函数的表
示方法
1.解析式法
3.图象法
2.列表法
课堂小结
https://www.21cnjy.com/help/help_extract.php
第十九章 一次函数
2021年春人教版八年级(下)数学
上节课我们学习了函数图象的意义和画函数图象的方法,这节课我们结合实例来总结画函数图象的一般步骤.
新课导入
(1)能用描点法画函数的图象.
(2)能从函数图象上看出函数与自变量的变化规律.
(3)知道函数的三种表示方法及它们的优缺点.
重点:用描点法画函数的图象,从函数图象上读取信息.
难点:从图象中说明函数的增减情况.
学习目标
定义:用解析式来表示函数关系的方法叫做解析式法.
解析式法
我们之前是怎么求函数解析式的?
想
想
一
探究新知
例1 汽车油箱中有汽油50L.如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,耗油量为0.1L/km.写出表示y与x的函数关系的式子.
分析:行驶路程x是自变量,邮箱中的油量y是x的函数,汽车的耗油量为0.1L/km,则x与y的关系为:
y=50-0.1x
例题讲解
考虑到x代表的实际意义为行驶路程,因此x不能取负数.而且行驶中的耗油量不能超过总的油量,所以有:
50-0.1x≥0
x≤500
0≤ x≤500
自变量的取值范围为:
完整的函数解析式为:
y=50-0.1x(0≤ x≤500)
例题讲解
思
考
用解析式法表示函数有什么优缺点?
解析式法简单明了,能够准确的反映整个变化过程中自变量与函数之间的对应关系,但有些实际问题中的函数关系,不能用解析式表示,如气温与时间的函数关系.
探究新知
用解析式法表示函数时需要注意什么?
1.函数解析式是一个等式;
2.是用含自变量的式子表示函数;
3.要确定自变量的取值范围.
探究新知
列表法
定义:用表格来表示函数关系的方法叫做列表法.
例2 在下列式子中,对于x的每一个确定的值,y都有唯一的对应值,即y是x的函数.从x的取值范围中选取一些数值,算出y的对应值,列表.
探究新知
(1)y=x+0.5
分析:从式子y=x+0.5可以看出,x取任意实数时这个式子都有意义,所以x的取值范围是全体实数.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
…
-3
-2
-1
0
1
2
3
…
y
…
-0.5
0.5
1.5
2.5
…
-2.5
-1.5
3.5
探究新知
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
…
0.5
1
1.5
2
2.5
3
3.5
4
5
6
…
y
…
6
3
2
1.5
…
12
4
2.4
1.2
1
(2) (x>0)
探究新知
思
考
用列表法表示函数有什么优缺点?
列表法一目了然,使用起来比较方便,但列出的对应值是有限的,不易看出自变量与函数之间的对应规律.
探究新知
用列表法与解析式法表示n边形的内角和和m(单位:度)关于边数n的函数.
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}边数n
3
4
5
6
7
…
内角和度数m
180
360
540
720
900
…
思路分析:绘制表格,从表格中得到内角和与边数的变化规律,再写出函数关系式.
针对练习
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}边数n
3
4
5
6
7
…
内角和度数m
180
360
540
720
900
…
边数增加1,内角和度数增加180°,所以n边形的内角和:m=180(n-2).
也就是说多边形的边数增加1,它的内角和就会增加180° .
针对练习
图象法
定义:用图象来表示函数关系的方法叫做图象法.
根据例2列出的表格,画出相应的函数图象.
探究新知
-2
(1)y=x+0.5
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
…
-3
-2
-1
0
1
2
3
…
y
…
-2.5
-1.5
-0.5
0.5
1.5
2.5
3.5
…
从函数图象可以看出,直线从左到右上升,即当x由小变大时,y=x+0.5随之增大.
O
x
y
1
1
-1
-1
y=x+0.5
2
2
-2
(2) (x>0)
从函数图象可以看出,曲线从左向右下降,即当x由小变大时,
随之减小.
(x>0)
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
…
0.5
1
1.5
2
2.5
3
3.5
4
5
6
…
y
…
6
3
2
1.5
…
12
4
2.4
1.2
1
O
x
y
6
2
1
3
4
5
1
2
3
4
5
6
(x>0)
思
考
用图象法表示函数有什么优缺点?
图象法形象直观,但只能近似的表达两个变量之间的函数关系.
1.用解析式法与图象法表示等边三角形的周长l关于边长a的函数.
解析式法:
等边三角形周长l=3a (a>0).
针对练习
函数l=3a??(a>0)的图象是过点O的射线(不含端点).图象又过点(1,3),故只要过点O和(1,3)作射线即可.(端点为虚点)
图象法:(如图所示)
2.一条小船沿直线向码头匀速前进.在0min,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.小船与码头的距离s是时间t的函数吗?如果是,写出函数解析式,并画出函数图象.如果船速不变,多长时间后小船到达码头?
解析:用表格列出s与t的对应关系,如下表
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
0
2
4
6
s
200
150
100
50
观察上表可得出x与s的关系式为:
s=200-25x(0≤x≤8)
所以小船与码头的距离s是时间t的函数.
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}t
0
2
4
6
s
200
150
100
50
画函数图象
O
s(m)
t(min)
50
2
100
150
200
4
6
8
由图象可知,在第8min时,小船与码头的距离为0,即船速不变时,8min后小船到达码头.
思
考
表示函数时,能不能只用一种方法?还是要结合同时使用几种方法?
例3 一个水库的水位在最近5h内持续上涨.下表记录了这5h内6个时间点的水位高度,其中t表示时间,y表示水位高度.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}t/h
0
1
2
3
4
5
y/m
3
3.3
3.6
3.9
4.2
4.5
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律吗?
例题讲解
下图所描出的是表中数据对应的点.
这些点在一条直线上.
水位越来越高.
水位高度y是否为时间t的函数?如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.这个函数能表示水位的变化规律吗?
y=0.3t+3(0≤t≤5)
能
(3)据估计这种上涨情况还会持续2h,预测再过2h水位高度将达到多少米?
再过2小时的水位高度,就是t=5+2=7时,
y=0.3t+3的函数值,
故有y=0.3×7+3=5.1(m),
也可利用函数图象估计出这个值.
归
纳
表示函数时,要根据具体情况选择适当的方法,有时为了全面的认识问题,需要同时使用几种方法.
1.向最大容量为60升的热水器内注水,每分钟注水10升,注水2分钟后停止注水1分钟,然后继续注水,直至注满.则能反映注水量与注水时间之间的函数关系的图象是( )
D
A
B
C
D
课堂练习
2.星期日上午9时小王从家中出发到距家900米处的书店买书,如图是9时~10时这段时间内他与家的距离随时间变化的图象.根据此图象,请你用简短的语句分别叙述小王在9时10分至9时15分与9时30分至9时50分这两段时间内活动的情况:
9时10分至9时15分: ;
9时30分至9时50分: .
在家
在书店买书
3.用描点法画出函数y=x+2的图象.
解:列表
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
-2
-1
0
1
2
y
0
1
2
3
4
、描点、连线后得到的图象如图所示.
4.用描点法画出函数y=-6x的图象.
解:列表
{93296810-A885-4BE3-A3E7-6D5BEEA58F35}x
-1
-?
0
?
1
y
6
3
0
-3
-6
并描点、连线后得到的图象如图所示.
5.弹簧的长度与所挂物体的质量的关系如图所示,观察图象回答:
(1)弹簧没挂物体的长度是多少?
解:当x=0时,y=10,即弹簧没挂物体的长度是10 cm.
(2)弹簧所挂物体的最大质量是多少?这时弹簧的长度是多少?
弹簧所挂物体的最大质量是20kg;
这时弹簧的长度为20cm.
函数的表
示方法
1.解析式法
3.图象法
2.列表法
课堂小结
https://www.21cnjy.com/help/help_extract.php
