六年级数学下册课件 - 圆柱、圆锥整理和复习 人教版(共35张PPT)
文档属性
| 名称 | 六年级数学下册课件 - 圆柱、圆锥整理和复习 人教版(共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-02 13:47:28 | ||
图片预览











文档简介
(共35张PPT)
圆柱、圆锥的整理和复习
圆柱、圆锥的整理和复习
把自己所归纳整理的有关圆柱、圆锥的知识告诉小组内的同学,看看小组内谁整理的知识最丰富,然后在自己的基础上完善。
交流要求:
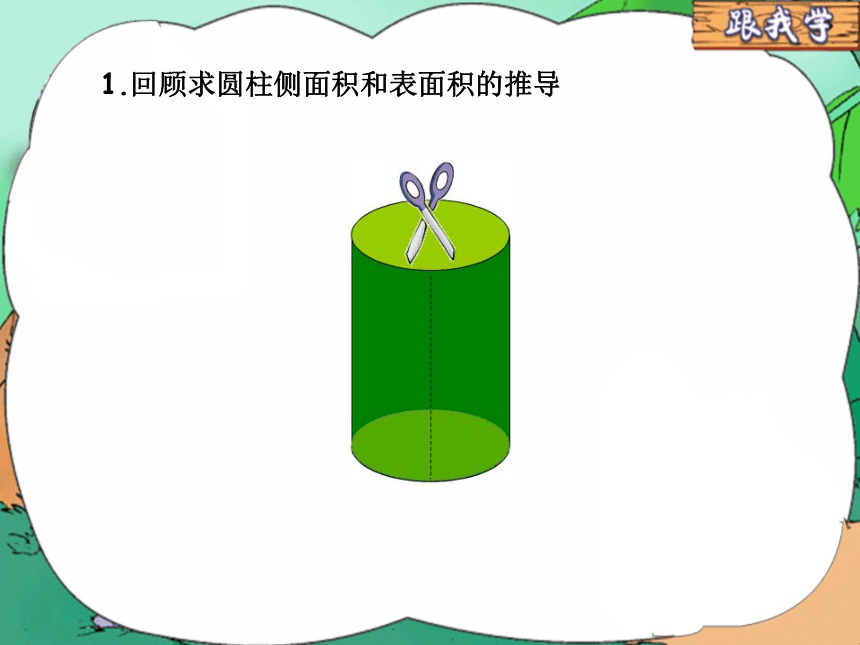
1.回顾求圆柱侧面积和表面积的推导
圆柱的表面积=圆柱的侧面积+两个底面的面积
圆柱的侧面积=底面周长×高
高
圆柱的体积=底面积×高
2.回顾圆柱体积计算方法的推导
3.回顾圆锥体积计算方法的推导
圆锥的体积等于与它等底等高的圆柱体积的三分之一。
一.我会填:
学以致用
(1).圆锥的底面是个(
)形,从圆锥的(
)到(
)的距离叫做圆锥的高。
圆
顶点
底面圆心
(2)如果一个圆柱与一个圆锥的底面积和高分别相等,那么圆柱与圆锥的体积比是(
)。
3:1
(3)一个圆锥的底面积是12平方分米,高是
9分米,它的体积是(
)立方分米。
36
×12×9=36
学以致用
一.我会填:
1
3
__
一.我会填:
学以致用
(4)一个圆柱形茶叶筒的侧面贴商标纸,圆柱的底面直径是10cm,高是20cm。这张商标纸展开后是一个长方形,它的长是(
)cm,宽是(
)cm.
31.4
20
长=底面周长:3.14×10=31.4
宽=高
一.我会填:
学以致用
(5)一张长方形纸片长10厘米,宽5厘米,以宽为轴旋转一周所得的图形是(
),它的底面积是(
)平方厘米,它的体积是(
)立方厘米.
圆柱
1570
314
底面积:3.14×102
=314
体积:314×5=1570
3.一个圆柱体和一个长方体的底面积和高分别相等,它们的体积也相等。(
)
二.我会判断:
√
4.
把一段圆柱形木料削成一个圆锥,削去部分是原来体积的三分之二.(
)
×
×
1.一个物体上、下两个面是相等的圆面,
那么它一定是圆柱形物体.(
)
2.圆柱的侧面展开后一定是长方形.(
)
×
最大的
三.我会选:
(1)下面是圆柱的展开图的是(
):
3
2
3
4
5
A
A.
B.
C.
5
9.42
2
2
4
12.56
长方形的长=底面周长
3.14×3=9.42
三.我会选:
(2)
一个圆柱形无盖的水桶
1.给这个水桶加个盖,是求圆柱的(
);
2.给这个水桶加个箍,是求圆柱的(
);
3.在这个无盖的水桶的外面涂上油漆,是求圆柱的(
);
4.这个水桶能装多少水?是求圆柱形水桶的(
)。
A
.
侧面
B.
底面
C
.
侧面+1个底面
D
.
底面周长
E
.表面积
F
.
体积
G
.
容积
B
D
C
G
三.我会选:
(3)等底等高的圆柱与圆锥,体积和是120平方厘米,圆柱的体积是(
)立方厘米;如果体积差是120立方厘米,圆柱的体积是(
)立方厘米。
A.360
B.
60
C.90
D.180
C
D
120÷4×3=90
体积比:3:1
120÷2×3=180
看到这根圆柱形木头,你能提出哪些有关的数学问题?
四.我会想:
四.我会想:
有一根圆柱形木头,直径是2分米,高是3分米。
(1)把这根木头横着放,滚动一圈,滚动的面积是多少?
(2)这根木头的体积是多少?
(3)把这根圆柱形的木头削成最大的圆锥形,这个圆锥形的体积是多少?削去的体积是多少?
(4)如果有一个跟它底面积相等,体积相等的圆锥木头,这个圆锥木头的高有多大?
谈谈你的收获!
圆柱、圆锥的整理和复习
圆柱、圆锥的整理和复习
把自己所归纳整理的有关圆柱、圆锥的知识告诉小组内的同学,看看小组内谁整理的知识最丰富,然后在自己的基础上完善。
交流要求:
1.回顾求圆柱侧面积和表面积的推导
圆柱的表面积=圆柱的侧面积+两个底面的面积
圆柱的侧面积=底面周长×高
高
圆柱的体积=底面积×高
2.回顾圆柱体积计算方法的推导
3.回顾圆锥体积计算方法的推导
圆锥的体积等于与它等底等高的圆柱体积的三分之一。
一.我会填:
学以致用
(1).圆锥的底面是个(
)形,从圆锥的(
)到(
)的距离叫做圆锥的高。
圆
顶点
底面圆心
(2)如果一个圆柱与一个圆锥的底面积和高分别相等,那么圆柱与圆锥的体积比是(
)。
3:1
(3)一个圆锥的底面积是12平方分米,高是
9分米,它的体积是(
)立方分米。
36
×12×9=36
学以致用
一.我会填:
1
3
__
一.我会填:
学以致用
(4)一个圆柱形茶叶筒的侧面贴商标纸,圆柱的底面直径是10cm,高是20cm。这张商标纸展开后是一个长方形,它的长是(
)cm,宽是(
)cm.
31.4
20
长=底面周长:3.14×10=31.4
宽=高
一.我会填:
学以致用
(5)一张长方形纸片长10厘米,宽5厘米,以宽为轴旋转一周所得的图形是(
),它的底面积是(
)平方厘米,它的体积是(
)立方厘米.
圆柱
1570
314
底面积:3.14×102
=314
体积:314×5=1570
3.一个圆柱体和一个长方体的底面积和高分别相等,它们的体积也相等。(
)
二.我会判断:
√
4.
把一段圆柱形木料削成一个圆锥,削去部分是原来体积的三分之二.(
)
×
×
1.一个物体上、下两个面是相等的圆面,
那么它一定是圆柱形物体.(
)
2.圆柱的侧面展开后一定是长方形.(
)
×
最大的
三.我会选:
(1)下面是圆柱的展开图的是(
):
3
2
3
4
5
A
A.
B.
C.
5
9.42
2
2
4
12.56
长方形的长=底面周长
3.14×3=9.42
三.我会选:
(2)
一个圆柱形无盖的水桶
1.给这个水桶加个盖,是求圆柱的(
);
2.给这个水桶加个箍,是求圆柱的(
);
3.在这个无盖的水桶的外面涂上油漆,是求圆柱的(
);
4.这个水桶能装多少水?是求圆柱形水桶的(
)。
A
.
侧面
B.
底面
C
.
侧面+1个底面
D
.
底面周长
E
.表面积
F
.
体积
G
.
容积
B
D
C
G
三.我会选:
(3)等底等高的圆柱与圆锥,体积和是120平方厘米,圆柱的体积是(
)立方厘米;如果体积差是120立方厘米,圆柱的体积是(
)立方厘米。
A.360
B.
60
C.90
D.180
C
D
120÷4×3=90
体积比:3:1
120÷2×3=180
看到这根圆柱形木头,你能提出哪些有关的数学问题?
四.我会想:
四.我会想:
有一根圆柱形木头,直径是2分米,高是3分米。
(1)把这根木头横着放,滚动一圈,滚动的面积是多少?
(2)这根木头的体积是多少?
(3)把这根圆柱形的木头削成最大的圆锥形,这个圆锥形的体积是多少?削去的体积是多少?
(4)如果有一个跟它底面积相等,体积相等的圆锥木头,这个圆锥木头的高有多大?
谈谈你的收获!
