六年级数学下册课件 圆锥的体积 人教版(共52张PPT)
文档属性
| 名称 | 六年级数学下册课件 圆锥的体积 人教版(共52张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-02 14:07:00 | ||
图片预览



文档简介
(共52张PPT)
复习:
圆柱体的体积=
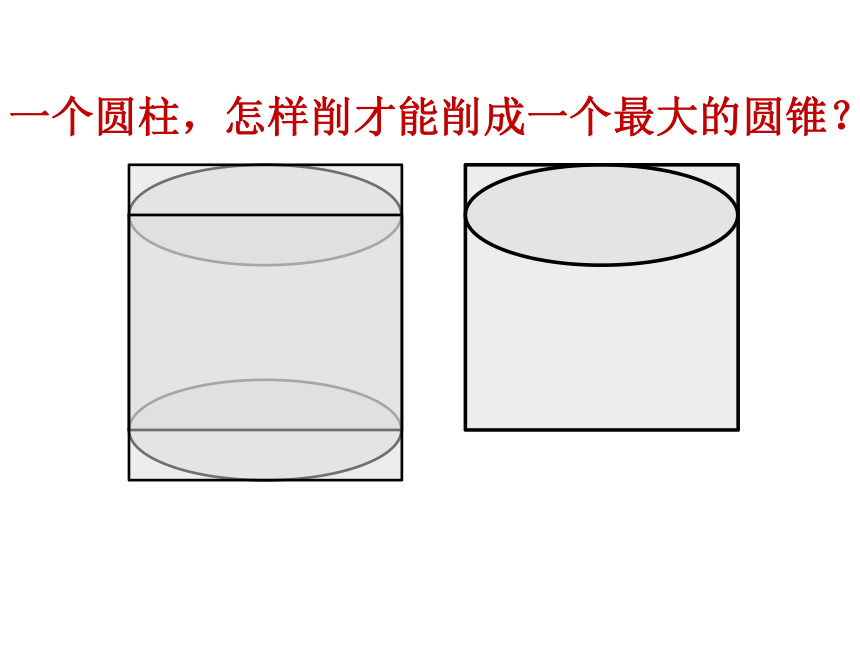
一个圆柱,怎样削才能削成一个最大的圆锥?
丰收的喜悦
V=
实验要求:
1.
在空圆柱里装满水倒入空圆锥里,观察要
几次正好倒完,并作好实验记录。
2.
把圆锥装满水倒进圆柱中,
观察要
几次才能倒满,并作好实验记录。
实验准备:
1套等底等高的圆锥、圆柱体容器,水,记录表。
实验1:
实验器材
一桶水、等底等高
的圆柱和圆锥各一个
?
实验过程
①在空圆柱里装满水倒入空圆锥里,( )次正好倒完。
①在空圆锥里装满水倒入空圆柱里,( )次正好装满。
结
论
②圆柱的体积等于与它(
)的
圆锥体积的(
)倍。
?
?
圆锥体积
计算公式
V锥=
②圆锥的体积等于与它(
)的
圆柱体积的
实验报告表
3
3
等底等高
等底等高
3
3
1
3
1
S
h
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
实验二:
实验准备:
不是等底等高的圆锥、圆柱体
容器,水。
?等底不等高的情况
?等高不等底的情况
通过两个实验,你们发现了什么?
圆柱的体积等于与它等底等高的
圆锥体积的3倍。
圆锥的体积等于与它等底等高的
圆柱体积的
。
小组讨论:
圆柱体积=底面积
高
1
3
圆锥体积=
底面积
高
小结
圆锥的体积等于和它等底等高的圆柱体积的三分之一
V=
sh
1
3
?
思考
?
要求圆锥的体积,必须知
道哪两个条件?为什么乘
?
3
1
V
=
s
h
3
1
底面积
和
高
底面半径
和
高
底面直径
和
高
底面周长
和
高
圆锥体积
计算圆锥的体积所必须的条件可以是:
如果小麦堆的底面半径为2m,高为1.5m。小麦堆的体积是多少立方米?
=6.28(m3)
答:小麦堆的体积是6.28m3。
1.底面积800平方米,高90米。求这堆沙子的体积。
2.
一个圆锥形的零件,底面周长是
18.84平方厘米,高是10厘米。这
个
零件的体积是多少?
3.计算下面各圆锥的体积。
4.
一个圆柱的体积是315立方厘米,与
它等底等高的圆锥的体积是多少立方
厘米?
练一练:
等底等高
1
24
×底面积×高
V=
s
h
一、填空:
1.圆锥的体积=(
),用字母表示是(
)。
2.圆柱体积的
与和它(
)的圆锥的体积相等。
3.一个圆柱和一个圆锥等底等高,圆柱的体积是3立方分米,圆锥的体积是(
)立方分米。
4.一个圆锥的底面积是12平方厘米,高是6厘米,体积是(
)立方厘米。
二、判断:
1.圆柱体的体积一定比圆锥体的体积大(
)
2.圆锥的体积等于与它等底等高的圆柱体的
(
)
3.正方体、长方体、圆锥体的体积都等于底面积×
高。
(
)
4.等底等高的圆柱和圆锥,如果圆柱体的体积是27立方米,那么圆锥的体积是9立方米。(
)
√
×
√
×
考考你:
2.
一个圆锥与一个圆柱等底等高,
已知圆柱与圆锥的体积和是36立
方米,
圆柱和圆锥的体积分别
是多少?
复习:
圆柱体的体积=
一个圆柱,怎样削才能削成一个最大的圆锥?
丰收的喜悦
V=
实验要求:
1.
在空圆柱里装满水倒入空圆锥里,观察要
几次正好倒完,并作好实验记录。
2.
把圆锥装满水倒进圆柱中,
观察要
几次才能倒满,并作好实验记录。
实验准备:
1套等底等高的圆锥、圆柱体容器,水,记录表。
实验1:
实验器材
一桶水、等底等高
的圆柱和圆锥各一个
?
实验过程
①在空圆柱里装满水倒入空圆锥里,( )次正好倒完。
①在空圆锥里装满水倒入空圆柱里,( )次正好装满。
结
论
②圆柱的体积等于与它(
)的
圆锥体积的(
)倍。
?
?
圆锥体积
计算公式
V锥=
②圆锥的体积等于与它(
)的
圆柱体积的
实验报告表
3
3
等底等高
等底等高
3
3
1
3
1
S
h
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
等底等高的:
实验二:
实验准备:
不是等底等高的圆锥、圆柱体
容器,水。
?等底不等高的情况
?等高不等底的情况
通过两个实验,你们发现了什么?
圆柱的体积等于与它等底等高的
圆锥体积的3倍。
圆锥的体积等于与它等底等高的
圆柱体积的
。
小组讨论:
圆柱体积=底面积
高
1
3
圆锥体积=
底面积
高
小结
圆锥的体积等于和它等底等高的圆柱体积的三分之一
V=
sh
1
3
?
思考
?
要求圆锥的体积,必须知
道哪两个条件?为什么乘
?
3
1
V
=
s
h
3
1
底面积
和
高
底面半径
和
高
底面直径
和
高
底面周长
和
高
圆锥体积
计算圆锥的体积所必须的条件可以是:
如果小麦堆的底面半径为2m,高为1.5m。小麦堆的体积是多少立方米?
=6.28(m3)
答:小麦堆的体积是6.28m3。
1.底面积800平方米,高90米。求这堆沙子的体积。
2.
一个圆锥形的零件,底面周长是
18.84平方厘米,高是10厘米。这
个
零件的体积是多少?
3.计算下面各圆锥的体积。
4.
一个圆柱的体积是315立方厘米,与
它等底等高的圆锥的体积是多少立方
厘米?
练一练:
等底等高
1
24
×底面积×高
V=
s
h
一、填空:
1.圆锥的体积=(
),用字母表示是(
)。
2.圆柱体积的
与和它(
)的圆锥的体积相等。
3.一个圆柱和一个圆锥等底等高,圆柱的体积是3立方分米,圆锥的体积是(
)立方分米。
4.一个圆锥的底面积是12平方厘米,高是6厘米,体积是(
)立方厘米。
二、判断:
1.圆柱体的体积一定比圆锥体的体积大(
)
2.圆锥的体积等于与它等底等高的圆柱体的
(
)
3.正方体、长方体、圆锥体的体积都等于底面积×
高。
(
)
4.等底等高的圆柱和圆锥,如果圆柱体的体积是27立方米,那么圆锥的体积是9立方米。(
)
√
×
√
×
考考你:
2.
一个圆锥与一个圆柱等底等高,
已知圆柱与圆锥的体积和是36立
方米,
圆柱和圆锥的体积分别
是多少?
