10.5 角平分线课件（共18张PPT）

第十章 三角形的有关证明
5 角平分线
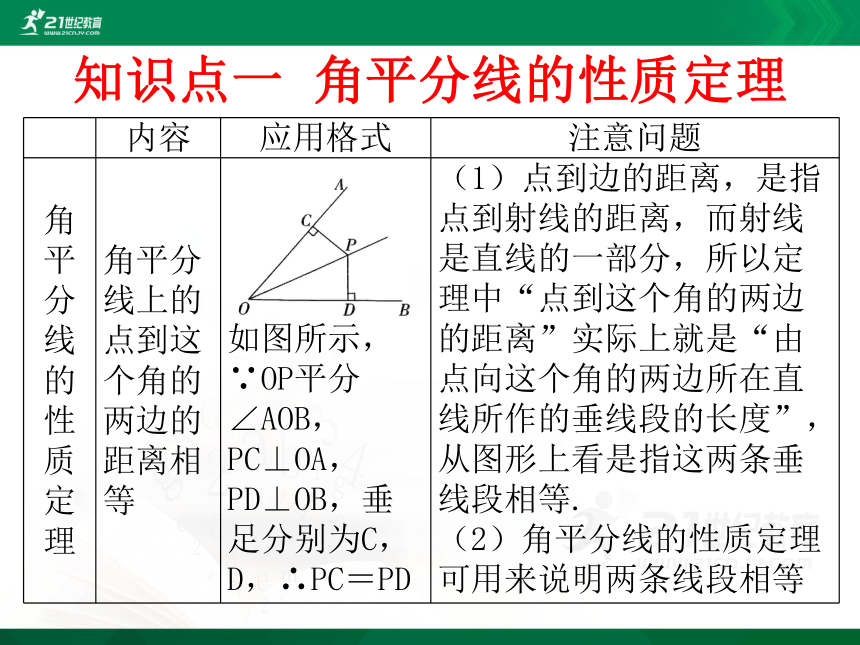
知识点一 角平分线的性质定理
内容
应用格式
注意问题
角平分线的性质定理
知识点一 角平分线的性质定理
内容
应用格式
注意问题
角平分线的性质定理
角平分线上的点到这个角的两边的距离相等

如图所示，∵OP平分∠AOB，PC⊥OA，PD⊥OB，垂足分别为C，D，∴PC＝PD
（1）点到边的距离，是指点到射线的距离，而射线是直线的一部分，所以定理中“点到这个角的两边的距离”实际上就是“由点向这个角的两边所在直线所作的垂线段的长度”，从图形上看是指这两条垂线段相等.
（2）角平分线的性质定理可用来说明两条线段相等
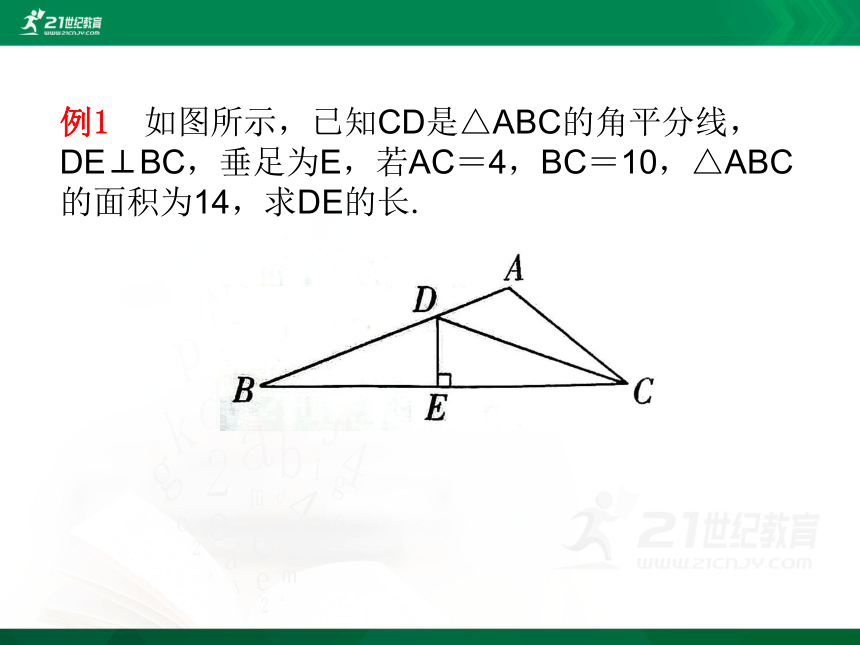
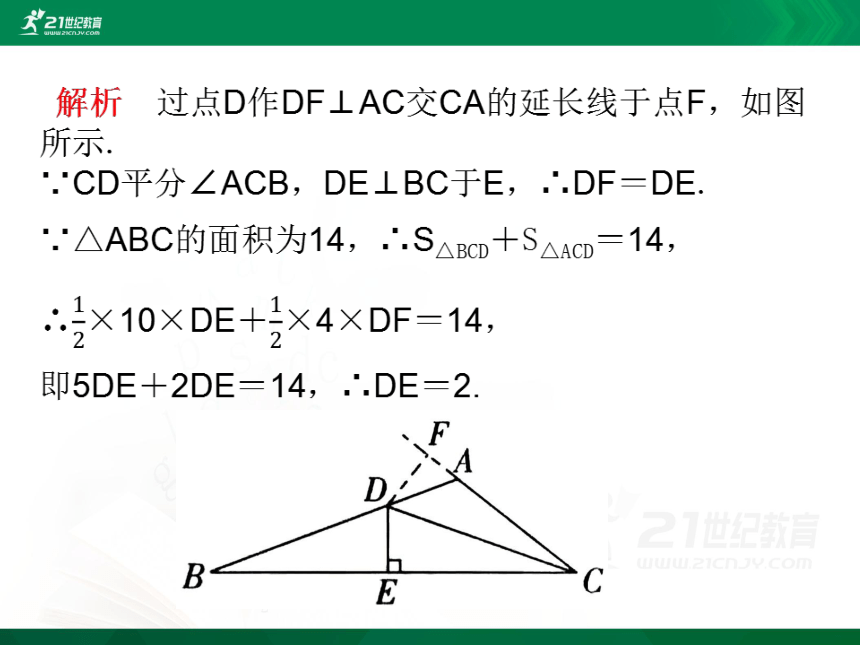
例1 如图所示，已知CD是△ABC的角平分线，DE⊥BC，垂足为E，若AC＝4，BC＝10，△ABC的面积为14，求DE的长.

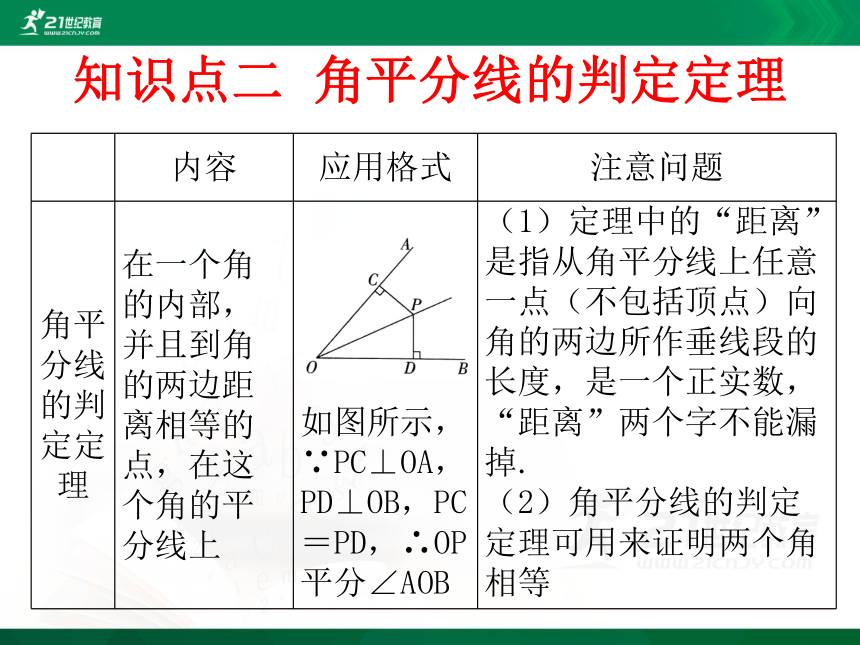
知识点二 角平分线的判定定理
内容
应用格式
注意问题
角平分线的判定定理
知识点二 角平分线的判定定理
内容
应用格式
注意问题
角平分线的判定定理
在一个角的内部，并且到角的两边距离相等的点，在这个角的平分线上

如图所示，∵PC⊥OA，PD⊥OB，PC＝PD，∴OP平分∠AOB
（1）定理中的“距离”是指从角平分线上任意一点（不包括顶点）向角的两边所作垂线段的长度，是一个正实数，“距离”两个字不能漏掉.
（2）角平分线的判定定理可用来证明两个角相等
例2 已知，如图所示，BD＝CD，BE⊥AC于点E，CF⊥AB于F求证:AD是∠BAC的平分线.



知识点三 三角形三个内角的平分线的性质
内容
图形
符号语言
三角形三个内角的平分线的性质
知识详解
知识点三 三角形三个内角的平分线的性质
内容
图形
符号语言
三角形三个内角的平分线的性质
三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等

若AD，BE，CF为△ABC的三条角平分线，则它们交于一点I，若IL⊥AB，IM⊥BC，IN⊥AC，垂足分别为L，M，N，则IL＝IM＝IN
知识详解
（1）三角形的三条角平分线的交点有且只有一个，且一定在三角形的内部.（2）在三角形内部，要找一点到三边的距离相等，只要作出两个角的平分线，其交点即是.（3）由角平分线的判定定理知这个性质的逆命题也是正确的，即在三角形内，到三角形三边的距离相等的点是三角形三条角平分线的交点是正确的
经典例题
题型一 角平分线的性质定理和判定定理的综合应用
例1 已知:如图所示，∠B＝∠C＝90°，
EB＝EC，DE平分∠ADC，
求证：AE是∠DAB的平分线.



题型一 角平分线的性质定理和判定定理的综合应用
证明 如图所示，过点E作EF⊥AD于F，
∵DE平分∠ADC，∠C＝90°，∴EC＝EF
∵EB＝EC，∴EF＝BE，
又∵∠B＝90°，
∴AE是∠DAB的平分线.
题型一 角平分线的性质定理和判定定理的综合应用
证明 如图所示，过点E作EF⊥AD于F，
∵DE平分∠ADC，∠C＝90°，∴EC＝EF
∵EB＝EC，∴EF＝BE，
又∵∠B＝90°，
∴AE是∠DAB的平分线.
点拨
注意角平分线的性质定理和判定定理的区别和联系.
题型二 角平分线与线段垂直平分线性质及判定的综合应用
例2 如图所示，在Rt△ABC中，∠C＝90°，BD平分∠ABC交AC于点D，DE垂直平分线段AB.
（1）求∠A的度数；
（2）若DE＝2cm，BD＝4cm，求AC的长.
解析 （1）∵DE是线段AB的垂直平分线，
∴AD＝BD，∴∠A＝∠DBE.
∵BD平分∠ABC，∴∠CBD＝∠DBE，
∴∠A＝∠DBE＝∠CBD，
∵∠C＝90°，∴∠A＝30°.
（2）∵∠C＝90°，∴DC⊥BC，
∵DE⊥BA，BD平分∠ABC，∴DC＝DE＝2cm，
∵DE垂直平分线段AB，∴AD＝BD＝4cm，
∴AC＝AD＋DC＝6cm.
解析 （1）∵DE是线段AB的垂直平分线，
∴AD＝BD，∴∠A＝∠DBE.
∵BD平分∠ABC，∴∠CBD＝∠DBE，
∴∠A＝∠DBE＝∠CBD，
∵∠C＝90°，∴∠A＝30°.
（2）∵∠C＝90°，∴DC⊥BC，
∵DE⊥BA，BD平分∠ABC，∴DC＝DE＝2cm，
∵DE垂直平分线段AB，∴AD＝BD＝4cm，
∴AC＝AD＋DC＝6cm.
点拨 经常利用角平分线的性质和线段垂直平分线的性质证明两条线段相等.