华东师大版七年级上册第4章 图形的初步认识小结与复习(一) 课件
文档属性
| 名称 | 华东师大版七年级上册第4章 图形的初步认识小结与复习(一) 课件 |  | |
| 格式 | rar | ||
| 文件大小 | 647.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-11 21:09:07 | ||
图片预览






文档简介
(共29张PPT)
第四章
小结与复习(一)
四、学好本章内容的要求
重要概念要做到“五会。”
(1)会表达:能正确地叙述概念的定义。
(2)会识图:能在较复杂的图形中识别出概念所反映的部分。
(3)会翻译:能结合图形把概念的定义翻译成符号语言。
(4)会画图:能画出概念所反映的几何图形,以及变式图形,会在图上标注字母或符号。
(5)会应用:能应用概念进行简单的判断、推理和计算。
学好本章内容的要求
重要概念要做到“五会”
(1)会表达:能正确地叙述概念的定义。
(2)会识图:能在较复杂的图形中识别出概念所反映的部分。
(3)会翻译:能结合图形把概念的定义翻译成符号语言。
(4)会画图:能画出概念所反映的几何图形,以及变式图形,会在图上标注字母或符号。
(5)会应用:能应用概念进行简单的判断、推理和计算。
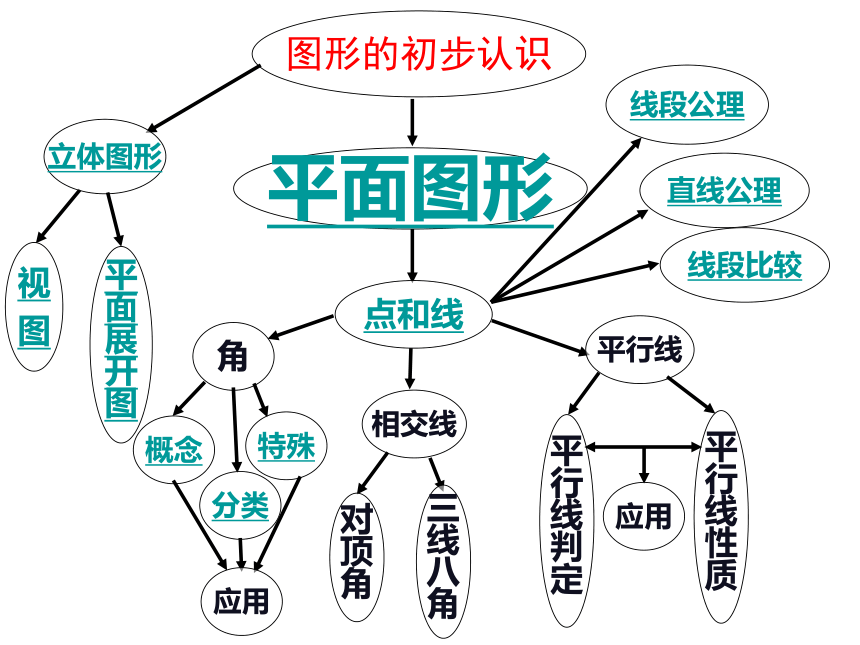
图形的初步认识
视
图
立体图形
平
面
展
开
图
角
平面图形
点和线
线段公理
直线公理
相交线
平行线
概念
分类
特殊
应用
对
顶
角
三
线
八
角
平
行
线
判
定
平
行
线
性
质
应用
线段比较
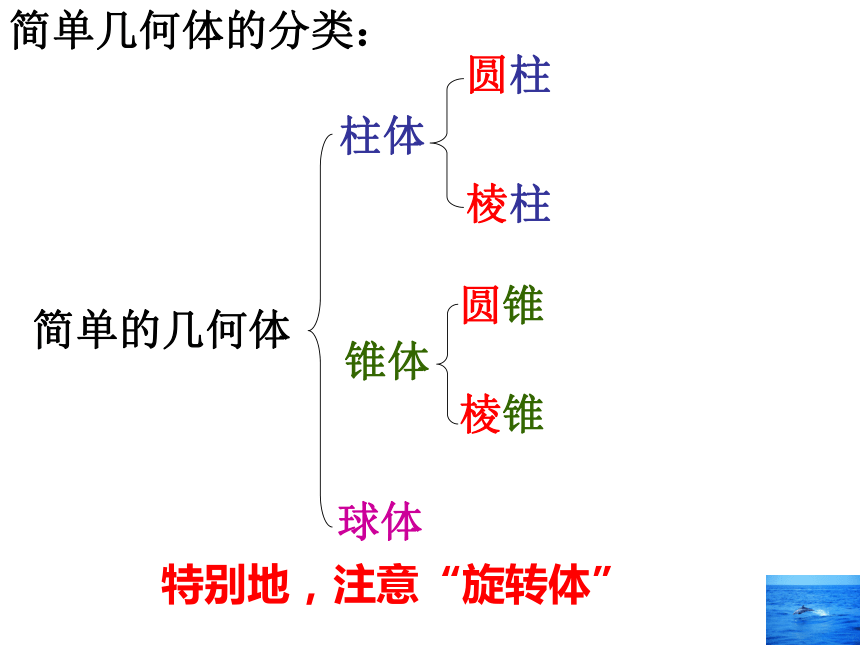
简单几何体的分类:
简单的几何体
柱体
锥体
球体
圆柱
棱柱
圆锥
棱锥
特别地,注意“旋转体”
从正面、上面和侧面(左面或右面)三个不同的方向看一个物体,然后描绘三张所看到的图,即视图,这样就把一个物体转化为平面的图形。
从正面看到的图形,称为正视图;
从上面看到的图形,称为俯视图;
从侧面看到的图形,称为侧视图,依观看方向不同,有左视图、右视图。
三视图
三视图的对应规律
主视图和俯视图长对正
主视图和左视图高平齐
俯视图和左视图宽相等
多面体:由平面图形围成的立体图形
把一个立体图形沿着某条线剪开,可以把立体图形的表面展开成一个平面图形,这个平面图形就称为这个立体的表面展开图。
多边形:由线段首尾相连围成的封闭的平面图形.
1.是平面图形.(不是立体图形)
2.由线段围成. (直的且首尾相连)
3.封闭图形. (不能有缺口)
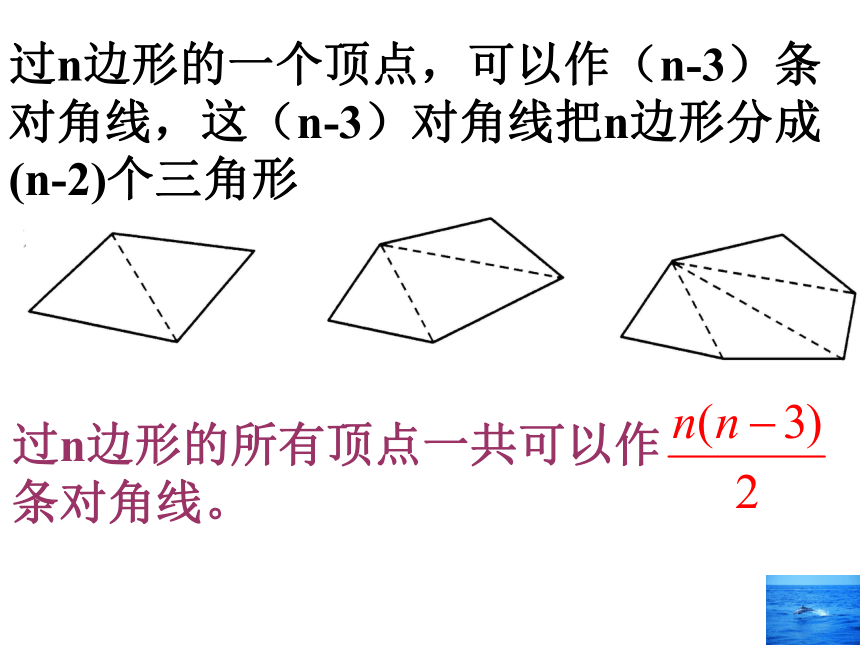
过n边形的一个顶点,可以作(n-3)条对角线,这(n-3)对角线把n边形分成(n-2)个三角形
过n边形的所有顶点一共可以作
条对角线。
点:没有大小,没有厚薄最基本的几何图形。用一个大写英文字母表示。
直线:平直的向两边无限延长的几何图形。用两个大写英文字母或一个小写英文字母表示。字母排列无顺序。
线段:直线上两点之间的部分叫做线段。与直线的表示形式一样。
射线:直线上一点一旁的部分叫做射线。射线的表示一般用两个大写英文字母表示。规定:端点字母写在前面(左),任意点字母写在后面(右)
线段公理
两点间线段最短
直线公理
两点确定一条直线
第二种方法是:叠合法
①
②
③
A
B
B
A
A
B
C
D
E
F
M
N
AB>CD
AB=EF
AB<MN
第一种方法是:度量法
把一条线段分成两条相等线段的点,叫做这条线段的中点。
线段的中点
A
B
C
如图,若C为线段AB的中点,则有如下等式成立:
(1)AC=CB
(2)AC=CB= AB
(3)AB=2AC=2CB
含义:“和”指线段数量的“和”与图形的“和”。“差”也如此。
线段的和与差
A
B
C
如图,
(1)AB=AC+CB
(2)AC=AB-CB
CB=AB-AC
注意:线段的“和”或者“差”仍然是一条线段
角的概念
角:
1.角是由两条有公共端点的射线组成的图形.
2.一条射线绕着它的端点旋转一周而成的图形.
角的专用符号:
“∠”
A
B
O
角的表示法(四种)
1.用三个大写英文字母。(顶点字母必须在中间)
2.用一个大写英文字母。(只能是顶点字母)
3.用一个阿拉伯数字。
4.用一个希腊小写字母。
或∠BOA
角的分类
锐角:大于0度而小于90度的角
直角:等于90度的角
钝角:大于90度小于180度的角
平角:等于180度的角
周角:等于360度的角
O
A
B
O
A
B
锐角
直角
钝角
平角
周角
O
A
(B)
角的度量单位:
1°=60 ′=3600 ″
例:5°= ′= ″;
38.15°= ° ′;
36″= ′= °
38°15′= °
度,分,秒
1°的60分之一为1分,记作“1′”,即1°=60′
1′的60分之一为1秒,记作“1″”,即1′=60″
角的度量工具:
量角器
300
1800
38
9
0.6
0.01
38.25
角的度量
如何比较两个角的大小呢?
(1) 度量法
(2) 叠合法
把∠ AEC移动,使它的顶点E移到和∠ BOD的顶点O重合,一边EA和DO重合,另一边OB和CE落在OD的同旁。
E
A
C
O
D
B
(1)如果AE与OB重合,那么∠AEC就等于∠ BOD,记作∠AEC= ∠BOD
E
A
C
O
B
D
(2)如果CE落在∠BOD的内部,那么∠AEC小于∠ BOD,记作∠AEC< ∠BOD
E
A
C
O
D
B
(3)如果AE落在∠BOD的外部,那么∠AEC大于∠ BOD,记作∠AEC> ∠BOD
E
A
C
O
D
B
在一张纸上画出一个角并剪下,将这个角对折,使其两边重合,折痕与角两边所成的两个角的大小有什么关系?
从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线
重要结论:如图,若OC平分∠AOB,则有
(1)∠AOC=∠BOC=0.5∠AOB
(2)∠AOB=2∠AOC=2∠BOC
O
C
A
B
角的加减运算
∠AOB=∠___+∠____
∠AOC=∠AOB-∠____
∠BOC=∠____-∠AOC
如果∠AOC=∠COB呢
互为余角
如果 的和是一个 ,那么这两个角叫做 余角,其中一个角是 的余角。
互为补角
如果 的和是一个 ,那么这两个角叫做 补角,其中一个角是 的补角。
两个角
直角
互为
另一个角
两个角
互为
另一个角
平角
补角性质:
同角或等角的补角相等。
余角性质:
同角或等角的余角相等。
两直线相交形成了∠1、∠2、∠3和∠4
其中的∠1和∠3叫做对顶角,∠2和∠4也是对顶角.
对顶角相等
教材P178复习题 A组全部,B组11,12,13
第四章
小结与复习(一)
四、学好本章内容的要求
重要概念要做到“五会。”
(1)会表达:能正确地叙述概念的定义。
(2)会识图:能在较复杂的图形中识别出概念所反映的部分。
(3)会翻译:能结合图形把概念的定义翻译成符号语言。
(4)会画图:能画出概念所反映的几何图形,以及变式图形,会在图上标注字母或符号。
(5)会应用:能应用概念进行简单的判断、推理和计算。
学好本章内容的要求
重要概念要做到“五会”
(1)会表达:能正确地叙述概念的定义。
(2)会识图:能在较复杂的图形中识别出概念所反映的部分。
(3)会翻译:能结合图形把概念的定义翻译成符号语言。
(4)会画图:能画出概念所反映的几何图形,以及变式图形,会在图上标注字母或符号。
(5)会应用:能应用概念进行简单的判断、推理和计算。
图形的初步认识
视
图
立体图形
平
面
展
开
图
角
平面图形
点和线
线段公理
直线公理
相交线
平行线
概念
分类
特殊
应用
对
顶
角
三
线
八
角
平
行
线
判
定
平
行
线
性
质
应用
线段比较
简单几何体的分类:
简单的几何体
柱体
锥体
球体
圆柱
棱柱
圆锥
棱锥
特别地,注意“旋转体”
从正面、上面和侧面(左面或右面)三个不同的方向看一个物体,然后描绘三张所看到的图,即视图,这样就把一个物体转化为平面的图形。
从正面看到的图形,称为正视图;
从上面看到的图形,称为俯视图;
从侧面看到的图形,称为侧视图,依观看方向不同,有左视图、右视图。
三视图
三视图的对应规律
主视图和俯视图长对正
主视图和左视图高平齐
俯视图和左视图宽相等
多面体:由平面图形围成的立体图形
把一个立体图形沿着某条线剪开,可以把立体图形的表面展开成一个平面图形,这个平面图形就称为这个立体的表面展开图。
多边形:由线段首尾相连围成的封闭的平面图形.
1.是平面图形.(不是立体图形)
2.由线段围成. (直的且首尾相连)
3.封闭图形. (不能有缺口)
过n边形的一个顶点,可以作(n-3)条对角线,这(n-3)对角线把n边形分成(n-2)个三角形
过n边形的所有顶点一共可以作
条对角线。
点:没有大小,没有厚薄最基本的几何图形。用一个大写英文字母表示。
直线:平直的向两边无限延长的几何图形。用两个大写英文字母或一个小写英文字母表示。字母排列无顺序。
线段:直线上两点之间的部分叫做线段。与直线的表示形式一样。
射线:直线上一点一旁的部分叫做射线。射线的表示一般用两个大写英文字母表示。规定:端点字母写在前面(左),任意点字母写在后面(右)
线段公理
两点间线段最短
直线公理
两点确定一条直线
第二种方法是:叠合法
①
②
③
A
B
B
A
A
B
C
D
E
F
M
N
AB>CD
AB=EF
AB<MN
第一种方法是:度量法
把一条线段分成两条相等线段的点,叫做这条线段的中点。
线段的中点
A
B
C
如图,若C为线段AB的中点,则有如下等式成立:
(1)AC=CB
(2)AC=CB= AB
(3)AB=2AC=2CB
含义:“和”指线段数量的“和”与图形的“和”。“差”也如此。
线段的和与差
A
B
C
如图,
(1)AB=AC+CB
(2)AC=AB-CB
CB=AB-AC
注意:线段的“和”或者“差”仍然是一条线段
角的概念
角:
1.角是由两条有公共端点的射线组成的图形.
2.一条射线绕着它的端点旋转一周而成的图形.
角的专用符号:
“∠”
A
B
O
角的表示法(四种)
1.用三个大写英文字母。(顶点字母必须在中间)
2.用一个大写英文字母。(只能是顶点字母)
3.用一个阿拉伯数字。
4.用一个希腊小写字母。
或∠BOA
角的分类
锐角:大于0度而小于90度的角
直角:等于90度的角
钝角:大于90度小于180度的角
平角:等于180度的角
周角:等于360度的角
O
A
B
O
A
B
锐角
直角
钝角
平角
周角
O
A
(B)
角的度量单位:
1°=60 ′=3600 ″
例:5°= ′= ″;
38.15°= ° ′;
36″= ′= °
38°15′= °
度,分,秒
1°的60分之一为1分,记作“1′”,即1°=60′
1′的60分之一为1秒,记作“1″”,即1′=60″
角的度量工具:
量角器
300
1800
38
9
0.6
0.01
38.25
角的度量
如何比较两个角的大小呢?
(1) 度量法
(2) 叠合法
把∠ AEC移动,使它的顶点E移到和∠ BOD的顶点O重合,一边EA和DO重合,另一边OB和CE落在OD的同旁。
E
A
C
O
D
B
(1)如果AE与OB重合,那么∠AEC就等于∠ BOD,记作∠AEC= ∠BOD
E
A
C
O
B
D
(2)如果CE落在∠BOD的内部,那么∠AEC小于∠ BOD,记作∠AEC< ∠BOD
E
A
C
O
D
B
(3)如果AE落在∠BOD的外部,那么∠AEC大于∠ BOD,记作∠AEC> ∠BOD
E
A
C
O
D
B
在一张纸上画出一个角并剪下,将这个角对折,使其两边重合,折痕与角两边所成的两个角的大小有什么关系?
从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线
重要结论:如图,若OC平分∠AOB,则有
(1)∠AOC=∠BOC=0.5∠AOB
(2)∠AOB=2∠AOC=2∠BOC
O
C
A
B
角的加减运算
∠AOB=∠___+∠____
∠AOC=∠AOB-∠____
∠BOC=∠____-∠AOC
如果∠AOC=∠COB呢
互为余角
如果 的和是一个 ,那么这两个角叫做 余角,其中一个角是 的余角。
互为补角
如果 的和是一个 ,那么这两个角叫做 补角,其中一个角是 的补角。
两个角
直角
互为
另一个角
两个角
互为
另一个角
平角
补角性质:
同角或等角的补角相等。
余角性质:
同角或等角的余角相等。
两直线相交形成了∠1、∠2、∠3和∠4
其中的∠1和∠3叫做对顶角,∠2和∠4也是对顶角.
对顶角相等
教材P178复习题 A组全部,B组11,12,13
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
