11.2.2全等三角形的判定(SAS)
文档属性
| 名称 | 11.2.2全等三角形的判定(SAS) |  | |
| 格式 | rar | ||
| 文件大小 | 250.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-02-11 22:56:08 | ||
图片预览



文档简介
(共17张PPT)
三角形全等的判定(3)
知识回顾:
判断三角形 全等的方法:
1.定义(重合)法;
2.SSS;
3.ASA;
4.AAS.
画出一个△ABC,使得AB=15cm, ∠B=60°,
BC=20cm,把你画的三角形剪下来,并与小组内其他同
学画的进行比较,它们会全等吗?
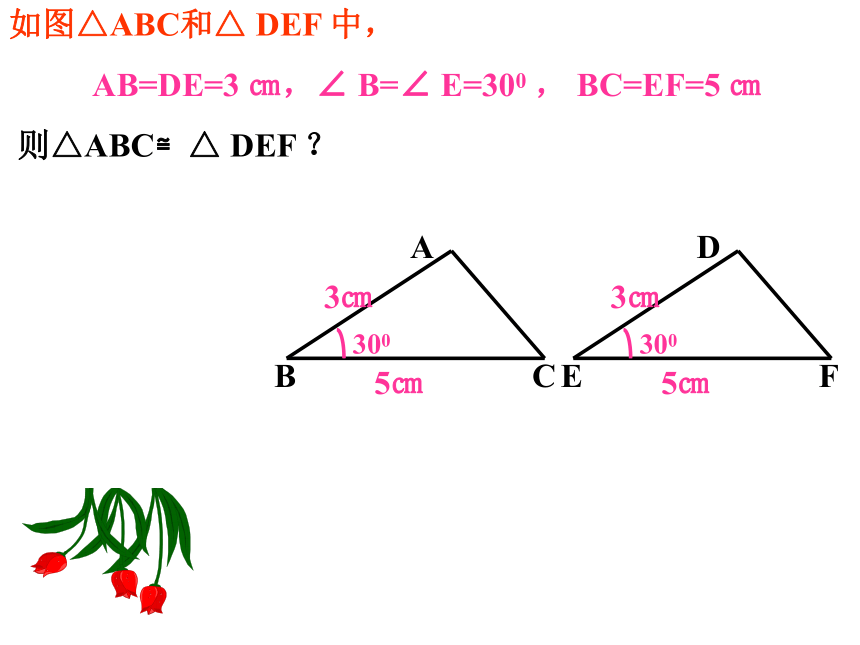
如图△ABC和△ DEF 中,
AB=DE=3 ㎝,∠ B=∠ E=300 , BC=EF=5 ㎝
则△ABC≌△ DEF ?
3㎝
5㎝
300
A
B
C
3㎝
5㎝
300
D
E
F
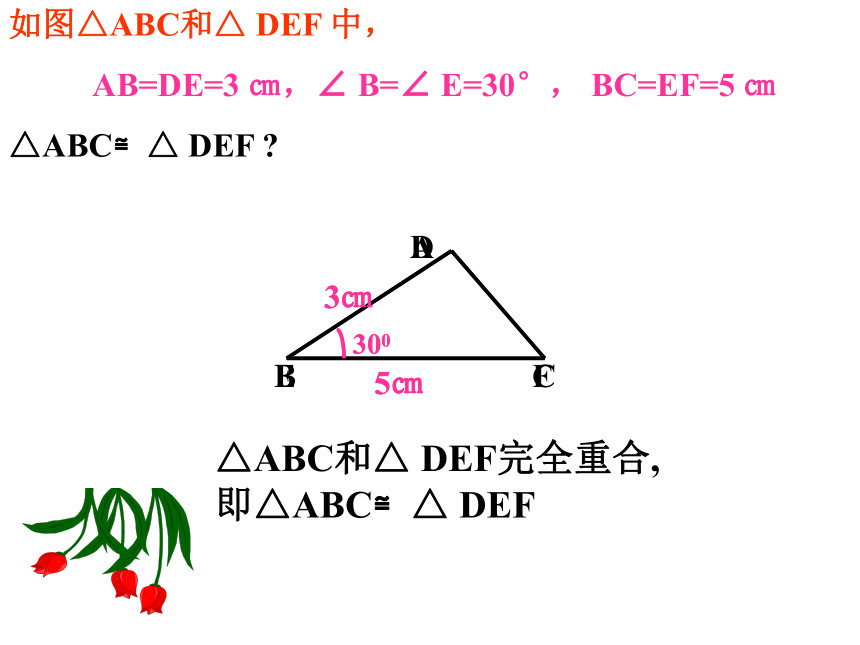
如图△ABC和△ DEF 中,
AB=DE=3 ㎝,∠ B=∠ E=30°, BC=EF=5 ㎝
△ABC≌△ DEF
3㎝
5㎝
300
A
B
C
3㎝
5㎝
300
D
E
F
△ABC和△ DEF完全重合,
即△ABC≌△ DEF
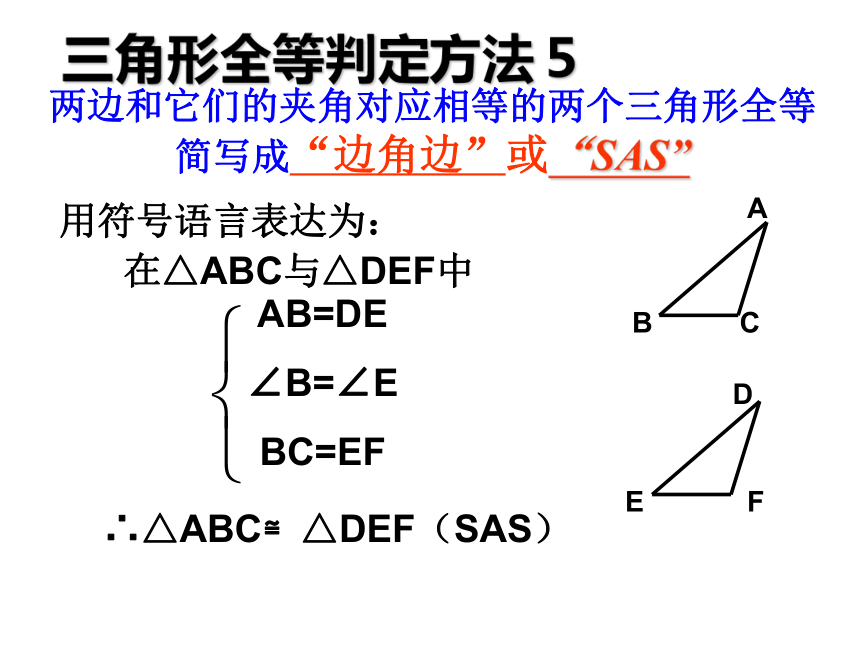
三角形全等判定方法5
用符号语言表达为:
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
A
B
C
D
E
F
两边和它们的夹角对应相等的两个三角形全等 简写成“边角边”或“SAS”
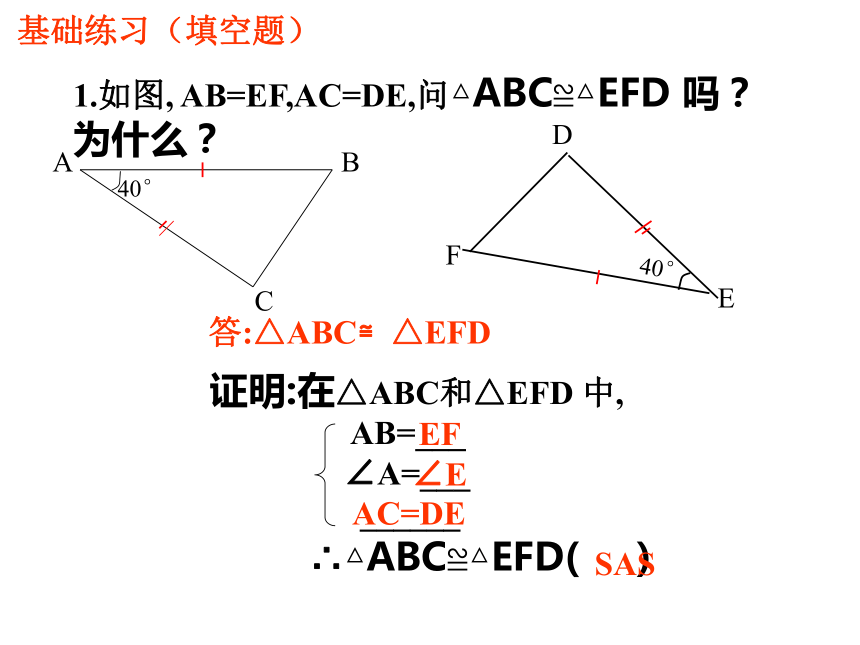
1.如图, AB=EF,AC=DE,问△ABC≌△EFD 吗?为什么?
A
B
C
40°
D
40°
E
F
证明:在△ABC和△EFD 中,
AB=___
∠A=___
______
∴△ABC≌△EFD( )
答:△ABC≌△EFD
EF
∠E
AC=DE
SAS
基础练习(填空题)
A
B
C
D
O
2.如图AC与BD相交于点O,
已知OA=OC,OB=OD,
求证:△AOB≌△COD
证明:
在△AOB和△COD中
OA=OC
______________
OB=OD
∠AOB=∠COD
∴△AOB≌△COD( )
SAS
已知:如图,AB=CB,∠1=∠2
△ABD 和△CBD 全等吗?
例1
A
B
C
D
1
2
变式1:已知:如图,AB=CB,∠1= ∠2
求证:(1) AD=CD (2)BD 平分∠ ADC
A
D
B
C
1
2
4
3
A
B
C
D
变式2:
已知:AD=CD,BD平分∠ADC
求证:∠A=∠C
1
2
归纳:证明两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到。
例2 如图,AC=BD,∠1= ∠2求证:BC=AD
变式1: 如图,AC=BD,BC=AD
求证:∠1= ∠2
A
B
C
D
1
2
A
B
C
D
1
2
变式2: 如图,AC=BD,BC=AD
求证:∠C=∠D
A
B
C
D
变式3: 如图,AC=BD,BC=AD
求证:∠A=∠B
A
B
C
D
巩固练习
1.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C
求证:∠A=∠D
E
C
D
B
F
A
2.如图,已知OA=OB,应填什么条件就得到:
△AOC≌ △BOD(只允许添加一个条件)
O
A
C
D
B
小结:
用符号语言表达为:
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
A
B
C
D
E
F
两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
到目前为止,我们一共探索出判定三角形全等的四种方法,它们分别是:
1、边边边(SSS)
3、角边角(ASA)
4、角角边(AAS)
2、边角边(SAS)
作业
P15 习题3
P16 习题9,10
三角形全等的判定(3)
知识回顾:
判断三角形 全等的方法:
1.定义(重合)法;
2.SSS;
3.ASA;
4.AAS.
画出一个△ABC,使得AB=15cm, ∠B=60°,
BC=20cm,把你画的三角形剪下来,并与小组内其他同
学画的进行比较,它们会全等吗?
如图△ABC和△ DEF 中,
AB=DE=3 ㎝,∠ B=∠ E=300 , BC=EF=5 ㎝
则△ABC≌△ DEF ?
3㎝
5㎝
300
A
B
C
3㎝
5㎝
300
D
E
F
如图△ABC和△ DEF 中,
AB=DE=3 ㎝,∠ B=∠ E=30°, BC=EF=5 ㎝
△ABC≌△ DEF
3㎝
5㎝
300
A
B
C
3㎝
5㎝
300
D
E
F
△ABC和△ DEF完全重合,
即△ABC≌△ DEF
三角形全等判定方法5
用符号语言表达为:
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
A
B
C
D
E
F
两边和它们的夹角对应相等的两个三角形全等 简写成“边角边”或“SAS”
1.如图, AB=EF,AC=DE,问△ABC≌△EFD 吗?为什么?
A
B
C
40°
D
40°
E
F
证明:在△ABC和△EFD 中,
AB=___
∠A=___
______
∴△ABC≌△EFD( )
答:△ABC≌△EFD
EF
∠E
AC=DE
SAS
基础练习(填空题)
A
B
C
D
O
2.如图AC与BD相交于点O,
已知OA=OC,OB=OD,
求证:△AOB≌△COD
证明:
在△AOB和△COD中
OA=OC
______________
OB=OD
∠AOB=∠COD
∴△AOB≌△COD( )
SAS
已知:如图,AB=CB,∠1=∠2
△ABD 和△CBD 全等吗?
例1
A
B
C
D
1
2
变式1:已知:如图,AB=CB,∠1= ∠2
求证:(1) AD=CD (2)BD 平分∠ ADC
A
D
B
C
1
2
4
3
A
B
C
D
变式2:
已知:AD=CD,BD平分∠ADC
求证:∠A=∠C
1
2
归纳:证明两条线段相等或两个角相等可以通过证明它们所在的两个三角形全等而得到。
例2 如图,AC=BD,∠1= ∠2求证:BC=AD
变式1: 如图,AC=BD,BC=AD
求证:∠1= ∠2
A
B
C
D
1
2
A
B
C
D
1
2
变式2: 如图,AC=BD,BC=AD
求证:∠C=∠D
A
B
C
D
变式3: 如图,AC=BD,BC=AD
求证:∠A=∠B
A
B
C
D
巩固练习
1.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C
求证:∠A=∠D
E
C
D
B
F
A
2.如图,已知OA=OB,应填什么条件就得到:
△AOC≌ △BOD(只允许添加一个条件)
O
A
C
D
B
小结:
用符号语言表达为:
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
A
B
C
D
E
F
两边和它们的夹角对应相等的两个三角形全等。简写成“边角边”或“SAS”
到目前为止,我们一共探索出判定三角形全等的四种方法,它们分别是:
1、边边边(SSS)
3、角边角(ASA)
4、角角边(AAS)
2、边角边(SAS)
作业
P15 习题3
P16 习题9,10
