2020-2021学年 北师大版八年级数学下册3.2图形的旋转优生辅导训练(word版含答案)
文档属性
| 名称 | 2020-2021学年 北师大版八年级数学下册3.2图形的旋转优生辅导训练(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 341.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-03 00:00:00 | ||
图片预览


文档简介
2020-2021年度北师大版八年级数学下册3.2图形的旋转优生辅导训练(附答案)
1.如图,将△ABC绕点A顺时针旋转一定的角度至△AB′C′处,使得点C恰好在线B′C′上,若∠ACB=75°,则∠BCB′的度数为( )
A.20°
B.25°
C.30°
D.35°
2.如图,在△ABC中,∠ABC=40°,在同一平面内,将△ABC绕点B逆时针旋转100°到△A′BC′的位置,则∠ABC′=( )
A.40°
B.60°
C.80°
D.100°
3.如图,在△ABC中,∠CAB=45°,将△ABC在平面内绕点A旋转到△A′B′C′的位置,若∠CAB′=25°,则旋转角的度数为( )
A.25°
B.20°
C.65°
D.70°
4.如图,将直角三角形ABC绕其直角顶点C顺时针旋转至△A′B′C′,已知AC=8,BC=6,点M,M′分别是AB,A′B′的中点,则MM′的长是( )
A.5
B.4
C.3
D.5
5.如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,下列结论正确的有( )个.
①△BED是等边三角形;②AE∥BC;③△ADE的周长等于BD+BC;④∠ADE=∠DBC.
A.1
B.2
C.3
D.4
6.如图,△ABC是直角三角形,∠B=30?,∠A=90?,AC=1,将△ABC绕点C逆时针旋转60?至△CB1A1,再将△CB1A1沿边B1C翻折至△CB1A2,则△ABC与△CB1A2重叠部分的面积为( )
A.
B.
C.
D.
7.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55°
B.60°
C.65°
D.70°
8.如图,在△ABC中,AB=5,BC=7,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长是( )
A.1
B.2
C.2.5
D.3
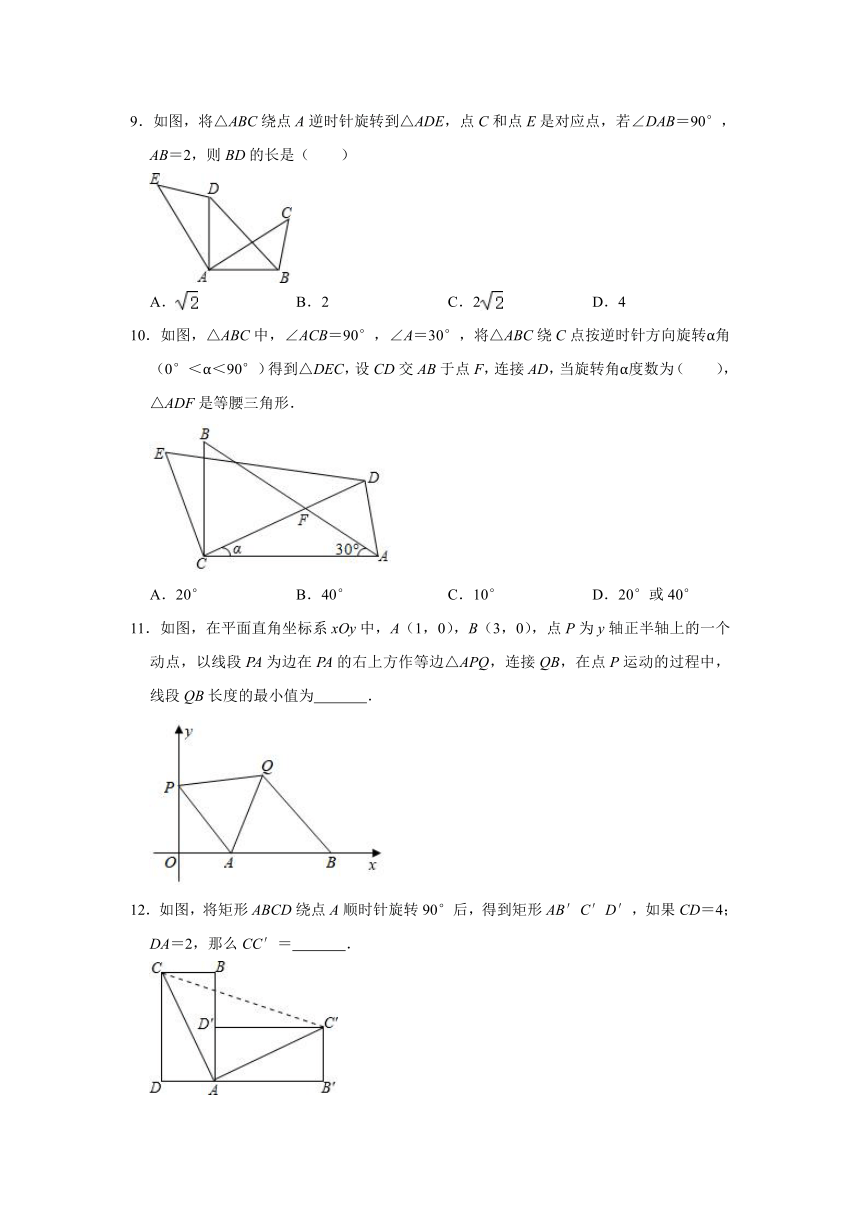
9.如图,将△ABC绕点A逆时针旋转到△ADE,点C和点E是对应点,若∠DAB=90°,AB=2,则BD的长是( )
A.
B.2
C.2
D.4
10.如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于点F,连接AD,当旋转角α度数为( ),△ADF是等腰三角形.
A.20°
B.40°
C.10°
D.20°或40°
11.如图,在平面直角坐标系xOy中,A(1,0),B(3,0),点P为y轴正半轴上的一个动点,以线段PA为边在PA的右上方作等边△APQ,连接QB,在点P运动的过程中,线段QB长度的最小值为
.
12.如图,将矩形ABCD绕点A顺时针旋转90°后,得到矩形AB′C′D′,如果CD=4;DA=2,那么CC′=
.
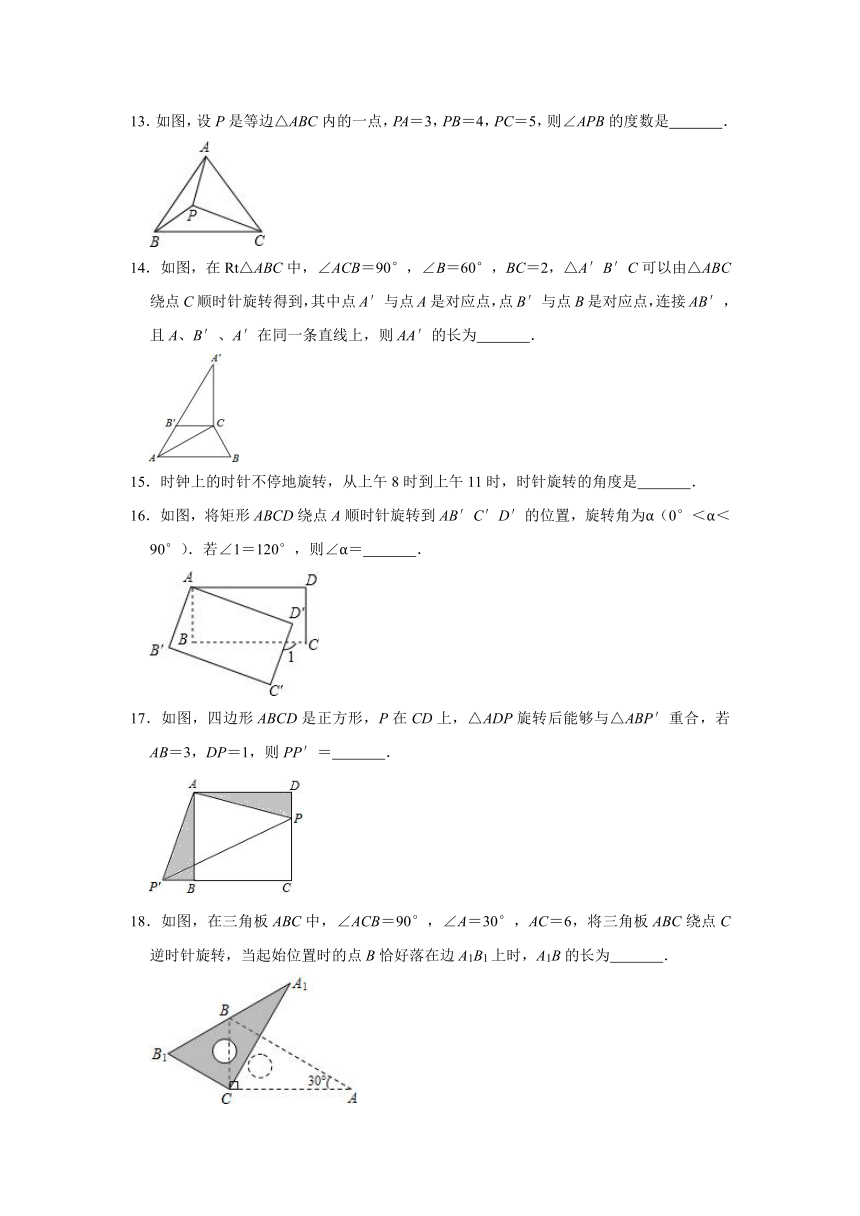
13.如图,设P是等边△ABC内的一点,PA=3,PB=4,PC=5,则∠APB的度数是
.
14.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为
.
15.时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的角度是
.
16.如图,将矩形ABCD绕点A顺时针旋转到AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=120°,则∠α=
.
17.如图,四边形ABCD是正方形,P在CD上,△ADP旋转后能够与△ABP′重合,若AB=3,DP=1,则PP′=
.
18.如图,在三角板ABC中,∠ACB=90°,∠A=30°,AC=6,将三角板ABC绕点C逆时针旋转,当起始位置时的点B恰好落在边A1B1上时,A1B的长为
.
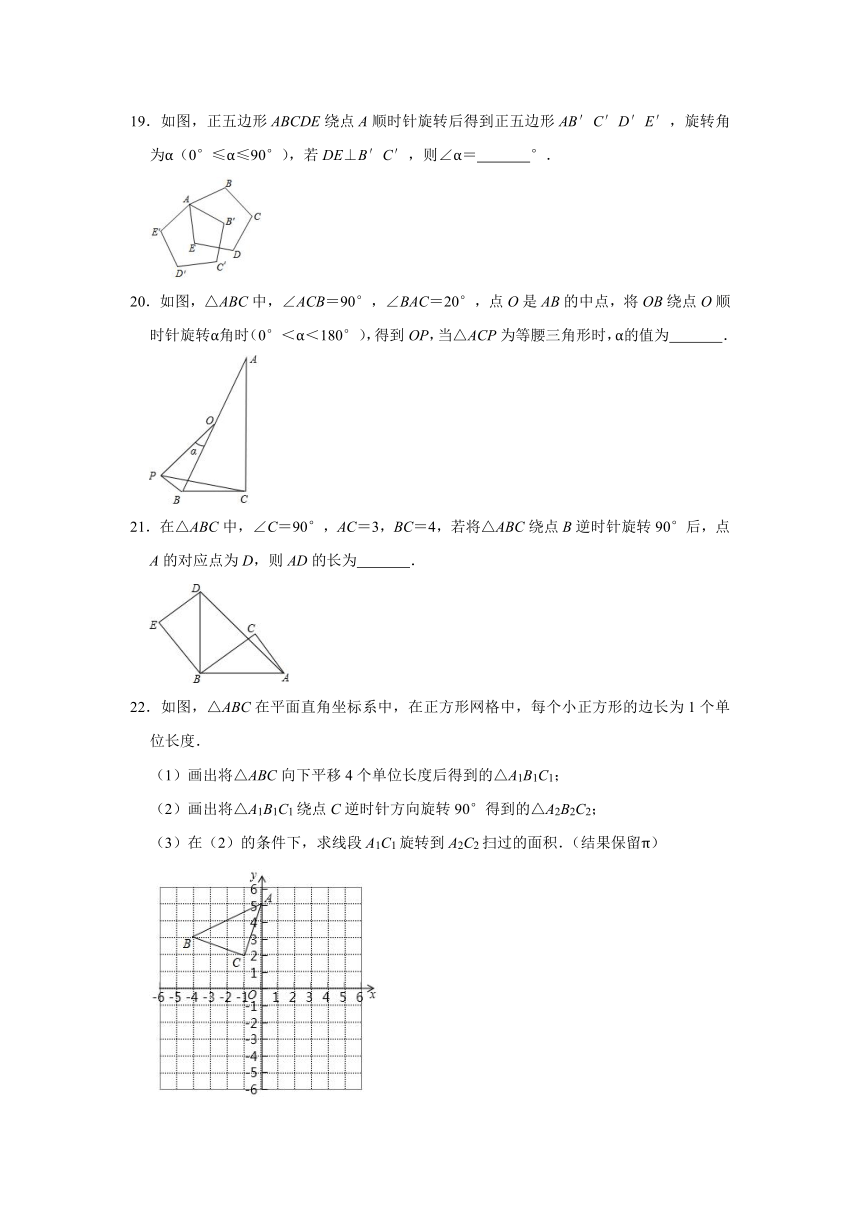
19.如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),若DE⊥B′C′,则∠α=
°.
20.如图,△ABC中,∠ACB=90°,∠BAC=20°,点O是AB的中点,将OB绕点O顺时针旋转α角时(0°<α<180°),得到OP,当△ACP为等腰三角形时,α的值为
.
21.在△ABC中,∠C=90°,AC=3,BC=4,若将△ABC绕点B逆时针旋转90°后,点A的对应点为D,则AD的长为
.
22.如图,△ABC在平面直角坐标系中,在正方形网格中,每个小正方形的边长为1个单位长度.
(1)画出将△ABC向下平移4个单位长度后得到的△A1B1C1;
(2)画出将△A1B1C1绕点C逆时针方向旋转90°得到的△A2B2C2;
(3)在(2)的条件下,求线段A1C1旋转到A2C2扫过的面积.(结果保留π)
23.如图①,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,点D在直线BC上,E在AC上,且AC=CD,DE=AB.
(1)如图②,将△ECD沿CB方向平移,使点E落在AB上,得△E1C1D1,求平移的距离;
(2)如图③,将△ECD绕点C逆时针旋转,使点E落在AB上,得△E2CD2,求旋转角∠DCD2的度数.
24.如图1,在△ABC中,∠C>∠B,AD为△ABC的角平分线,DE⊥BC且交AB于点E.
(1)求证:∠C﹣∠B=2∠ADE;
(2)如图2,将图1中的直线DE向右平移经过点A,记为AF.将射线FC绕点F逆时针方向旋转一个角度α(0°<α<90°),旋转后的射线记为FM,FM交AC于点M.再将射线FB绕点F顺时针方向旋转同一个角度α,旋转后的射线记为FN,FN交AB于点N.请直接写出∠AMF、∠ANF、∠DAF之间的数量关系.
25.如图,在Rt△ABC中,∠CAB=90°,点P是△ABC内一点,将△ABP绕点A逆时针旋转后能与△ACP′重合,如果AP=3,求PP′的长.
26.如图,在Rt△ABC中,∠A=60°,将△ABC绕点C顺时针旋转60°,点A、B的对应点分别为D、E.
(1)求证:△BCE为等边三角形;
(2)若点F为边AC的中点,连接DF,猜想DF与BE的数量关系,并证明.
27.如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.
28.如图,AM∥BN,∠MAB和∠NBA的角平分线相交于点P,过点P作直线EF分别交AM、BN于F、E.
(1)求证:AB=AF+BE;
(2)若EF绕点P旋转,F在MA的延长线上滑动,如图,请你测量,猜想AB、AF、BE之间的关系,写出这个关系式,并加以证明.
参考答案
1.解:∵将△ABC绕点A顺时针旋转一定的角度至△AB′C′处
∴AC=AC',∠ACB=∠AC'B'=75°
∴∠ACC'=∠AC'B'=75°
∴∠ACB'=105°
∵∠BCB'=∠ACB'﹣∠ACB
∴∠BCB'=105°﹣75°=30°
故选:C.
2.解:∵将△ABC绕点B逆时针旋转100°到△A′BC′的位置,
∴∠A'BC'=∠ABC=40°,∠ABA'=100°
∴∠ABC'=60°
故选:B.
3.解:∵∠CAB=45°,∠CAB′=25°,
∴∠B′AB=∠CAB﹣∠CAB′=45°﹣25°=20°,
∴旋转角的度数为20°,
故选:B.
4.解:连接CM,CM′,
∵AC=8,BC=6,
∴AB==10,
∵M是AB的中点,
∴CM=AB=5,
∵Rt△ABC绕点C顺时针旋转90°得到Rt△A′B′C,
∴∠A′CM′=∠ACM
∵∠ACM+∠MCB=90°,
∴∠MCB+∠BCM′=90°,
又∵CM=C′M′,
∴△CMM′是等腰直角三角形,
∴MM′=CM=5
故选:A.
5.解:∵将△BCD绕点B逆时针旋转60°,得到△BAE,
∴BE=BD,∠EBD=60°,AE=CD,∠EAB=∠C=60°,
∴△BED是等边三角形,
故①正确;
∵∠BAE=∠C=∠ABC=60°,
∴AE∥BC,
故②正确;
∵△BED是等边三角形,
∴DE=BD,∠EDB=60°,
∴△ADE的周长=AE+AD+DE=CD+AD+DE=AC+BD=BC+BD,
故③正确;
∵∠ADB=∠C+∠DBC,
∴∠ADE+60°=∠DBC+60°,
∴∠ADE=∠DBC,
故④正确.
故选:D.
6.解:
∵∠B=30?,∠BAC=90?,AC=1,
∴BC=2,AB=AC=
∵将△ABC绕点C逆时针旋转60?至△CB1A1,再将△CB1A1沿边B1C翻折至△CB1A2,
∴A1C=AC=1=A2C,∠BAC=∠A1=∠B1A2C=90°
∴A2B=1,且∠B=30°
∴A2E=
∴△ABC与△CB1A2重叠部分的面积=﹣×1×=
故选:C.
7.解:∵将△ABC绕点C顺时针旋转90°得到△EDC.
∴∠DCE=∠ACB=20°,∠BCD=∠ACE=90°,AC=CE,
∴∠CAD=45°,∠ACD=90°﹣20°=70°,
∴∠ADC=180°﹣45°﹣70°=65°,
故选:C.
8.解:∵将△ABC绕点A按顺时针旋转一定角度得到△ADE,
∴AD=AB,
∵∠B=60°,
∴△ABD是等边三角形,
∴BD=AB,
∵AB=5,BC=7,
∴CD=BC﹣BD=7﹣5=2.
故选:B.
9.解:∵△ABC绕点A逆时针旋转到△ADE,点C和点E是对应点,
∴AB=AD=2,
∵∠DAB=90°,
∴△ABD为等腰直角三角形,
∴BD=AB=2.
故选:C.
10.解:∵△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,
∴∠DCA=α,CD=CA,
∴∠CDA=∠CAD=(180°﹣α)=90°﹣α,
∵△ADF是等腰三角形,∠DFA=30°+α,
①CD=CA,则∠CDA=∠CAD,
当FD=FA,则∠FDA=∠FAD,这不合题意舍去,
②当AF=AD,
∴∠ADF=∠AFD,
∴90°﹣α=30°+α,
解得α=40°;
③当DF=DA,
∴∠DFA=∠DAF,
∴30°+α=90°﹣α﹣30°,
解得α=20°.
故选:D.
11.解:如图,将△ABQ绕点A逆时针旋转60°到△ACP,连接BC,
∴△ABQ≌△ACP,
∴AB=AC,BQ=PC,∠PAQ=∠BAC,
∵△ABC是等边三角形
∴∠PAQ=∠BAC=60°,
∴△ABC是等边三角形,
∵A(1,0),B(3,0),
∴AB=3﹣1=2,
∴C(2,),即点C是定点,
∴当PC最小时,BQ最小,
∴当PC⊥y轴时,PC最小,最小值是2,
∴线段QB长度的最小值为2.
故答案为:2.
12.解:由旋转的性质可知,∠CAC′=90°,AC=AC′,
Rt△ACD中,由勾股定理得,
AC===2,
在Rt△CAC′中,由勾股定理得,
CC′==2.
故答案为:2.
13.解:∵△ABC为等边三角形,
∴BA=BC,
可将△BPC绕点B逆时针旋转60°得△BEA,
连EP,如图,
∴BE=BP=4,AE=PC=5,∠PBE=60°,
∴△BPE为等边三角形,
∴PE=PB=4,∠BPE=60°,
在△AEP中,AE=5,AP=3,PE=4,
∴AE2=PE2+PA2,
∴△APE为直角三角形,且∠APE=90°,
∴∠APB=90°+60°=150°.
故答案为150°.
14.解:∵在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,
∴∠CAB=30°,故AB=4,
∵△A′B′C由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,
∴AB=A′B′=4,AC=A′C,
∴∠CAA′=∠A′=30°,
∴∠ACB′=∠B′AC=30°,
∴AB′=B′C=2,
∴AA′=2+4=6,
故答案为6.
15.解:∵周角为360°,时针12小时转一周,
∴每小时对应的角度为:360°÷12=30°.
∵时针从上午8时到上午11时走了三个小时,
∴时针旋转的角度是:30°×3=90°.
故答案为:90°.
16.解:如图,由对顶角相等得,∠2=∠1=120°,
在四边形中,∠BAD′=360°﹣90°×2﹣∠2=360°﹣180°﹣120°=60°,
所以,∠DAD′=90°﹣60°=30°,
即旋转角∠α=∠DAD′=30°.
故答案为:30°.
17.解:∵四边形ABCD是正方形,
∴AB=AD=3,∠ABC=∠D=∠BAD=90°,
∴AP==,
∵△ADP旋转后能够与△ABP′重合,
∴△ADP≌△ABP′,
∴AP′=AP=,∠BAP′=∠DAP,
∴∠PAP′=∠BAD=90°,
∴△PAP′是等腰直角三角形,
∴PP′=AP=2;
故答案为:2.
18.解:∵∠ACB=90°,∠A=30°,AC=6,
∴∠B=60°,BC=AC=2,AB=4.
∵由旋转的性质可知:∠B1=∠B=60°,B1C=BC,A1B1=AB=4,
∴△BCB1是等边三角形.
∴BB1=BC=2.
∴BA1=A1B1﹣B1B=4﹣2=2.
故答案为:2.
19.解:DE与B′C′相交于O点,如图,
∵五边形ABCDE为正五边形,
∴∠B=∠BAE=∠E==108°,
∵正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),
∴∠BAB′=α,∠B′=∠B=108°,
∵DE⊥B′C′,
∴∠B′OE=90°,
∴∠B′AE=360°﹣∠B′﹣∠E﹣∠B′OE=360°﹣108°﹣108°﹣90°=54°,
∴∠BAB′=∠BAE﹣∠B′AE=108°﹣54°=54°,
即∠α=54°.
故答案为54.
20.解:连接AP,如图,
∵点O是AB的中点,
∴OA=OB,
∵OB绕点O顺时针旋转α角时(0°<α<180°),得到OP,
∴OP=OB,
∴点P在以AB为直径的圆上,
∴∠BAP=∠BOP=α,∠APC=∠ABC=70°,
∵∠ACB=90°,
∴点P、C在以AB为直径的圆上,
∴∠ACP=∠ABP=90°﹣α,∠APC=∠ABC=70°,
当AP=AC时,∠APC=∠ACP,
即90°﹣α=70°,解得α=40°;
当PA=PC时,∠PAC=∠ACP,
即α+20°=90°﹣α,解得α=70°;
当CP=CA时,∠CAP=∠CAP,
即α+20°=70°,解得α=100°,
综上所述,α的值为40°或70°或100°.
故答案为40°或70°或100°.
21.解:∵∠C=90°,AC=3,BC=4,
∴AB==5,
∵将△ABC绕点B逆时针旋转90°后,点A的对应点为D,
∴AB=BD=5,
则在Rt△ABD中,AD的长为:=5.
故答案为:5.
22.解:(1)如图△A1B1C1为所作;
(2)如图△A2B2C2为所作;
(3)线段旋转后扫过的面积为.
23.(1)解:∵∠ACB=90°
∴∠ECD=90°,
∵AC=CD,DE=AB.
∴Rt△ACB≌Rt△DCE(HL),
∴BC=CE,
∵∠A=30°,AB=4,
∴BC=AB=2,
∴CE=2,
由平移知,C1E1∥AC,C1E1=CE=2,
∴∠BE1C1=∠A=30°,
∴BE1=2BC1,
∴BE12﹣BC12=C1E12,
即:4BC12﹣BC12=4,
∴BC1=,
∴CC1=BC﹣BC1=2﹣;
即平移距离为2﹣.
(2)解:旋转角∠DCD2的度数是△ECD绕点C旋转的度数,即∠ECE2的度数;
∵∠ABC=60°,BC=CE2=2,AB=4,
∴△E2BC是等边三角形,
∴BC=E2C=E2B=2,
∴AE2=E2C=2,
∴∠E2AC=∠E2CA,
∴∠ECE2=∠BAC=30°,
∴∠DCD2=∠ECE2=30°.
24.(1)证明:如图1中,
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD.
又∵∠C+∠ADC+∠CAD=180°,∠B+∠ADB+∠BAD=180°,
∴∠C﹣∠B=∠ADB﹣∠ADC,
∵ED⊥BC,
∴∠BDE=∠CDE=90°,
∵∠ADB=∠BDE+∠ADE,∠ADC=∠CDE﹣∠ADE,
∴∠ADB﹣∠ADC=2∠ADE,
∴∠C﹣∠B=2∠ADE.
(2)解:结论:∠AMF﹣∠ANF=2∠DAF.
理由:如图2中,作DE∥AF交AB于E.
∵∠AMF=∠MFC+∠C,∠ANF=∠B+∠BFN,∠MFC=∠NFB=α,
∴∠AMF﹣∠ANF=(∠MFC+∠C)﹣(∠B+∠NFB)=∠C﹣∠B,
由(1)可知∠C﹣∠B=2∠ADE,
∵DE∥AF,
∴∠ADE=∠DAF,
∴∠AMF﹣∠ANF=2∠DAF.
25.解:∵将△ABP绕点A逆时针旋转后能与△ACP′重合,
∴△ABP≌△ACP′,
∴AP=AP′=3,∠BAP=∠CAP′,
∵∠BAC=90°,
∴∠BAP+∠CAP=90°,
∴∠CAP′+∠CAP=90°,
即∠PAP′=90°,
∴△PAP′是等腰直角三角形,
由勾股定理得:PP′==3,
即PP′的长是3.
26.(1)证明:∵将△ABC绕点C顺时针旋转60°得到△DEC,
∴∠BCE=∠ACD=60°,CB=CE,
∴△BCE是等边三角形;
(2)DF=BE.
证明:连接BF,
∵点F是边AC中点,
∴CF=BF=AF=AC,
∵∠A=60°,
∴∠BCA=30°,
∴BA=AC,
∴BF=AB=AF=CF,
∵将△ABC绕点C顺时针旋转60°,点A、B的对应点分别为D、E.
∴AB=DE,
∴DE=BF.
延长BF交CE于点G,则∠BGE=∠GBC+∠BCG=90°,
∴∠BGE=∠DEC,
∴BF∥ED,
∴四边形BEDF是平行四边形,
∴DF=BE.
27.(1)证明:∵将△ABD绕点A逆时针旋转60°得△ACE
∴△ABD≌△ACE,∠BAC=∠DAE,
∴AD=AE,BD=CE,∠AEC=∠ADB=120°,
∵△ABC为等边三角形
∴∠BAC=60°
∴∠DAE=60°
∴△ADE为等边三角形,
∴AD=DE,
(2)∠ADC=90°,∠AEC=120°,∠DAE=60°
∴∠DCE=360°﹣∠ADC﹣∠AEC﹣∠DAE=90°,
(3)∵△ADE为等边三角形
∴∠ADE=60°
∴∠CDE=∠ADC﹣∠ADE=30°
又∵∠DCE=90°
∴DE=2CE=2BD=2,
∴AD=DE=2
在Rt△DCE中,.
28.(1)证明:延长AP交BE于Q,
∵AP平分∠MAB,
∴∠MAP=∠BAP,
∵AM∥BN,
∴∠MAP=∠AQB,
∴∠BAP=∠AQB,
∴AB=BQ,
∵BP平分∠ABE,
∴AP=PQ,
∵AM∥BN,
∴==1,
∴AF=EQ,
∴AB=AF+BE;
(2)①成立,
证明:如图2,
延长AP交BE于Q,
∵AP平分∠MAB,
∴∠MAP=∠BAP,
∵AM∥BN,
∴∠MAP=∠AQB,
∴∠BAP=∠AQB,
∴AB=BQ,
∵BP平分∠ABE,
∴AP=PQ,
∵AM∥BN,
∴==1,
∴AF=EQ,
∴AB=AF+BE;
②不同,猜想:AF+AB=BE,
证明:延长AP交BE于Q,
∵AP平分∠MAB,
∴∠MAP=∠BAP,
∵AM∥BN,
∴∠MAP=∠AQB,
∴∠BAP=∠AQB,
∴AB=BQ,
∵BP平分∠ABE,
∴AP=PQ,
∵AM∥BN,
∴==1,
∴AF=EQ,
∴AF+AB=BE
1.如图,将△ABC绕点A顺时针旋转一定的角度至△AB′C′处,使得点C恰好在线B′C′上,若∠ACB=75°,则∠BCB′的度数为( )
A.20°
B.25°
C.30°
D.35°
2.如图,在△ABC中,∠ABC=40°,在同一平面内,将△ABC绕点B逆时针旋转100°到△A′BC′的位置,则∠ABC′=( )
A.40°
B.60°
C.80°
D.100°
3.如图,在△ABC中,∠CAB=45°,将△ABC在平面内绕点A旋转到△A′B′C′的位置,若∠CAB′=25°,则旋转角的度数为( )
A.25°
B.20°
C.65°
D.70°
4.如图,将直角三角形ABC绕其直角顶点C顺时针旋转至△A′B′C′,已知AC=8,BC=6,点M,M′分别是AB,A′B′的中点,则MM′的长是( )
A.5
B.4
C.3
D.5
5.如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,下列结论正确的有( )个.
①△BED是等边三角形;②AE∥BC;③△ADE的周长等于BD+BC;④∠ADE=∠DBC.
A.1
B.2
C.3
D.4
6.如图,△ABC是直角三角形,∠B=30?,∠A=90?,AC=1,将△ABC绕点C逆时针旋转60?至△CB1A1,再将△CB1A1沿边B1C翻折至△CB1A2,则△ABC与△CB1A2重叠部分的面积为( )
A.
B.
C.
D.
7.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55°
B.60°
C.65°
D.70°
8.如图,在△ABC中,AB=5,BC=7,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长是( )
A.1
B.2
C.2.5
D.3
9.如图,将△ABC绕点A逆时针旋转到△ADE,点C和点E是对应点,若∠DAB=90°,AB=2,则BD的长是( )
A.
B.2
C.2
D.4
10.如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于点F,连接AD,当旋转角α度数为( ),△ADF是等腰三角形.
A.20°
B.40°
C.10°
D.20°或40°
11.如图,在平面直角坐标系xOy中,A(1,0),B(3,0),点P为y轴正半轴上的一个动点,以线段PA为边在PA的右上方作等边△APQ,连接QB,在点P运动的过程中,线段QB长度的最小值为
.
12.如图,将矩形ABCD绕点A顺时针旋转90°后,得到矩形AB′C′D′,如果CD=4;DA=2,那么CC′=
.
13.如图,设P是等边△ABC内的一点,PA=3,PB=4,PC=5,则∠APB的度数是
.
14.如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为
.
15.时钟上的时针不停地旋转,从上午8时到上午11时,时针旋转的角度是
.
16.如图,将矩形ABCD绕点A顺时针旋转到AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=120°,则∠α=
.
17.如图,四边形ABCD是正方形,P在CD上,△ADP旋转后能够与△ABP′重合,若AB=3,DP=1,则PP′=
.
18.如图,在三角板ABC中,∠ACB=90°,∠A=30°,AC=6,将三角板ABC绕点C逆时针旋转,当起始位置时的点B恰好落在边A1B1上时,A1B的长为
.
19.如图,正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),若DE⊥B′C′,则∠α=
°.
20.如图,△ABC中,∠ACB=90°,∠BAC=20°,点O是AB的中点,将OB绕点O顺时针旋转α角时(0°<α<180°),得到OP,当△ACP为等腰三角形时,α的值为
.
21.在△ABC中,∠C=90°,AC=3,BC=4,若将△ABC绕点B逆时针旋转90°后,点A的对应点为D,则AD的长为
.
22.如图,△ABC在平面直角坐标系中,在正方形网格中,每个小正方形的边长为1个单位长度.
(1)画出将△ABC向下平移4个单位长度后得到的△A1B1C1;
(2)画出将△A1B1C1绕点C逆时针方向旋转90°得到的△A2B2C2;
(3)在(2)的条件下,求线段A1C1旋转到A2C2扫过的面积.(结果保留π)
23.如图①,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,点D在直线BC上,E在AC上,且AC=CD,DE=AB.
(1)如图②,将△ECD沿CB方向平移,使点E落在AB上,得△E1C1D1,求平移的距离;
(2)如图③,将△ECD绕点C逆时针旋转,使点E落在AB上,得△E2CD2,求旋转角∠DCD2的度数.
24.如图1,在△ABC中,∠C>∠B,AD为△ABC的角平分线,DE⊥BC且交AB于点E.
(1)求证:∠C﹣∠B=2∠ADE;
(2)如图2,将图1中的直线DE向右平移经过点A,记为AF.将射线FC绕点F逆时针方向旋转一个角度α(0°<α<90°),旋转后的射线记为FM,FM交AC于点M.再将射线FB绕点F顺时针方向旋转同一个角度α,旋转后的射线记为FN,FN交AB于点N.请直接写出∠AMF、∠ANF、∠DAF之间的数量关系.
25.如图,在Rt△ABC中,∠CAB=90°,点P是△ABC内一点,将△ABP绕点A逆时针旋转后能与△ACP′重合,如果AP=3,求PP′的长.
26.如图,在Rt△ABC中,∠A=60°,将△ABC绕点C顺时针旋转60°,点A、B的对应点分别为D、E.
(1)求证:△BCE为等边三角形;
(2)若点F为边AC的中点,连接DF,猜想DF与BE的数量关系,并证明.
27.如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.
28.如图,AM∥BN,∠MAB和∠NBA的角平分线相交于点P,过点P作直线EF分别交AM、BN于F、E.
(1)求证:AB=AF+BE;
(2)若EF绕点P旋转,F在MA的延长线上滑动,如图,请你测量,猜想AB、AF、BE之间的关系,写出这个关系式,并加以证明.
参考答案
1.解:∵将△ABC绕点A顺时针旋转一定的角度至△AB′C′处
∴AC=AC',∠ACB=∠AC'B'=75°
∴∠ACC'=∠AC'B'=75°
∴∠ACB'=105°
∵∠BCB'=∠ACB'﹣∠ACB
∴∠BCB'=105°﹣75°=30°
故选:C.
2.解:∵将△ABC绕点B逆时针旋转100°到△A′BC′的位置,
∴∠A'BC'=∠ABC=40°,∠ABA'=100°
∴∠ABC'=60°
故选:B.
3.解:∵∠CAB=45°,∠CAB′=25°,
∴∠B′AB=∠CAB﹣∠CAB′=45°﹣25°=20°,
∴旋转角的度数为20°,
故选:B.
4.解:连接CM,CM′,
∵AC=8,BC=6,
∴AB==10,
∵M是AB的中点,
∴CM=AB=5,
∵Rt△ABC绕点C顺时针旋转90°得到Rt△A′B′C,
∴∠A′CM′=∠ACM
∵∠ACM+∠MCB=90°,
∴∠MCB+∠BCM′=90°,
又∵CM=C′M′,
∴△CMM′是等腰直角三角形,
∴MM′=CM=5
故选:A.
5.解:∵将△BCD绕点B逆时针旋转60°,得到△BAE,
∴BE=BD,∠EBD=60°,AE=CD,∠EAB=∠C=60°,
∴△BED是等边三角形,
故①正确;
∵∠BAE=∠C=∠ABC=60°,
∴AE∥BC,
故②正确;
∵△BED是等边三角形,
∴DE=BD,∠EDB=60°,
∴△ADE的周长=AE+AD+DE=CD+AD+DE=AC+BD=BC+BD,
故③正确;
∵∠ADB=∠C+∠DBC,
∴∠ADE+60°=∠DBC+60°,
∴∠ADE=∠DBC,
故④正确.
故选:D.
6.解:
∵∠B=30?,∠BAC=90?,AC=1,
∴BC=2,AB=AC=
∵将△ABC绕点C逆时针旋转60?至△CB1A1,再将△CB1A1沿边B1C翻折至△CB1A2,
∴A1C=AC=1=A2C,∠BAC=∠A1=∠B1A2C=90°
∴A2B=1,且∠B=30°
∴A2E=
∴△ABC与△CB1A2重叠部分的面积=﹣×1×=
故选:C.
7.解:∵将△ABC绕点C顺时针旋转90°得到△EDC.
∴∠DCE=∠ACB=20°,∠BCD=∠ACE=90°,AC=CE,
∴∠CAD=45°,∠ACD=90°﹣20°=70°,
∴∠ADC=180°﹣45°﹣70°=65°,
故选:C.
8.解:∵将△ABC绕点A按顺时针旋转一定角度得到△ADE,
∴AD=AB,
∵∠B=60°,
∴△ABD是等边三角形,
∴BD=AB,
∵AB=5,BC=7,
∴CD=BC﹣BD=7﹣5=2.
故选:B.
9.解:∵△ABC绕点A逆时针旋转到△ADE,点C和点E是对应点,
∴AB=AD=2,
∵∠DAB=90°,
∴△ABD为等腰直角三角形,
∴BD=AB=2.
故选:C.
10.解:∵△ABC绕C点按逆时针方向旋转α角(0°<α<90°)得到△DEC,
∴∠DCA=α,CD=CA,
∴∠CDA=∠CAD=(180°﹣α)=90°﹣α,
∵△ADF是等腰三角形,∠DFA=30°+α,
①CD=CA,则∠CDA=∠CAD,
当FD=FA,则∠FDA=∠FAD,这不合题意舍去,
②当AF=AD,
∴∠ADF=∠AFD,
∴90°﹣α=30°+α,
解得α=40°;
③当DF=DA,
∴∠DFA=∠DAF,
∴30°+α=90°﹣α﹣30°,
解得α=20°.
故选:D.
11.解:如图,将△ABQ绕点A逆时针旋转60°到△ACP,连接BC,
∴△ABQ≌△ACP,
∴AB=AC,BQ=PC,∠PAQ=∠BAC,
∵△ABC是等边三角形
∴∠PAQ=∠BAC=60°,
∴△ABC是等边三角形,
∵A(1,0),B(3,0),
∴AB=3﹣1=2,
∴C(2,),即点C是定点,
∴当PC最小时,BQ最小,
∴当PC⊥y轴时,PC最小,最小值是2,
∴线段QB长度的最小值为2.
故答案为:2.
12.解:由旋转的性质可知,∠CAC′=90°,AC=AC′,
Rt△ACD中,由勾股定理得,
AC===2,
在Rt△CAC′中,由勾股定理得,
CC′==2.
故答案为:2.
13.解:∵△ABC为等边三角形,
∴BA=BC,
可将△BPC绕点B逆时针旋转60°得△BEA,
连EP,如图,
∴BE=BP=4,AE=PC=5,∠PBE=60°,
∴△BPE为等边三角形,
∴PE=PB=4,∠BPE=60°,
在△AEP中,AE=5,AP=3,PE=4,
∴AE2=PE2+PA2,
∴△APE为直角三角形,且∠APE=90°,
∴∠APB=90°+60°=150°.
故答案为150°.
14.解:∵在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,
∴∠CAB=30°,故AB=4,
∵△A′B′C由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,
∴AB=A′B′=4,AC=A′C,
∴∠CAA′=∠A′=30°,
∴∠ACB′=∠B′AC=30°,
∴AB′=B′C=2,
∴AA′=2+4=6,
故答案为6.
15.解:∵周角为360°,时针12小时转一周,
∴每小时对应的角度为:360°÷12=30°.
∵时针从上午8时到上午11时走了三个小时,
∴时针旋转的角度是:30°×3=90°.
故答案为:90°.
16.解:如图,由对顶角相等得,∠2=∠1=120°,
在四边形中,∠BAD′=360°﹣90°×2﹣∠2=360°﹣180°﹣120°=60°,
所以,∠DAD′=90°﹣60°=30°,
即旋转角∠α=∠DAD′=30°.
故答案为:30°.
17.解:∵四边形ABCD是正方形,
∴AB=AD=3,∠ABC=∠D=∠BAD=90°,
∴AP==,
∵△ADP旋转后能够与△ABP′重合,
∴△ADP≌△ABP′,
∴AP′=AP=,∠BAP′=∠DAP,
∴∠PAP′=∠BAD=90°,
∴△PAP′是等腰直角三角形,
∴PP′=AP=2;
故答案为:2.
18.解:∵∠ACB=90°,∠A=30°,AC=6,
∴∠B=60°,BC=AC=2,AB=4.
∵由旋转的性质可知:∠B1=∠B=60°,B1C=BC,A1B1=AB=4,
∴△BCB1是等边三角形.
∴BB1=BC=2.
∴BA1=A1B1﹣B1B=4﹣2=2.
故答案为:2.
19.解:DE与B′C′相交于O点,如图,
∵五边形ABCDE为正五边形,
∴∠B=∠BAE=∠E==108°,
∵正五边形ABCDE绕点A顺时针旋转后得到正五边形AB′C′D′E′,旋转角为α(0°≤α≤90°),
∴∠BAB′=α,∠B′=∠B=108°,
∵DE⊥B′C′,
∴∠B′OE=90°,
∴∠B′AE=360°﹣∠B′﹣∠E﹣∠B′OE=360°﹣108°﹣108°﹣90°=54°,
∴∠BAB′=∠BAE﹣∠B′AE=108°﹣54°=54°,
即∠α=54°.
故答案为54.
20.解:连接AP,如图,
∵点O是AB的中点,
∴OA=OB,
∵OB绕点O顺时针旋转α角时(0°<α<180°),得到OP,
∴OP=OB,
∴点P在以AB为直径的圆上,
∴∠BAP=∠BOP=α,∠APC=∠ABC=70°,
∵∠ACB=90°,
∴点P、C在以AB为直径的圆上,
∴∠ACP=∠ABP=90°﹣α,∠APC=∠ABC=70°,
当AP=AC时,∠APC=∠ACP,
即90°﹣α=70°,解得α=40°;
当PA=PC时,∠PAC=∠ACP,
即α+20°=90°﹣α,解得α=70°;
当CP=CA时,∠CAP=∠CAP,
即α+20°=70°,解得α=100°,
综上所述,α的值为40°或70°或100°.
故答案为40°或70°或100°.
21.解:∵∠C=90°,AC=3,BC=4,
∴AB==5,
∵将△ABC绕点B逆时针旋转90°后,点A的对应点为D,
∴AB=BD=5,
则在Rt△ABD中,AD的长为:=5.
故答案为:5.
22.解:(1)如图△A1B1C1为所作;
(2)如图△A2B2C2为所作;
(3)线段旋转后扫过的面积为.
23.(1)解:∵∠ACB=90°
∴∠ECD=90°,
∵AC=CD,DE=AB.
∴Rt△ACB≌Rt△DCE(HL),
∴BC=CE,
∵∠A=30°,AB=4,
∴BC=AB=2,
∴CE=2,
由平移知,C1E1∥AC,C1E1=CE=2,
∴∠BE1C1=∠A=30°,
∴BE1=2BC1,
∴BE12﹣BC12=C1E12,
即:4BC12﹣BC12=4,
∴BC1=,
∴CC1=BC﹣BC1=2﹣;
即平移距离为2﹣.
(2)解:旋转角∠DCD2的度数是△ECD绕点C旋转的度数,即∠ECE2的度数;
∵∠ABC=60°,BC=CE2=2,AB=4,
∴△E2BC是等边三角形,
∴BC=E2C=E2B=2,
∴AE2=E2C=2,
∴∠E2AC=∠E2CA,
∴∠ECE2=∠BAC=30°,
∴∠DCD2=∠ECE2=30°.
24.(1)证明:如图1中,
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD.
又∵∠C+∠ADC+∠CAD=180°,∠B+∠ADB+∠BAD=180°,
∴∠C﹣∠B=∠ADB﹣∠ADC,
∵ED⊥BC,
∴∠BDE=∠CDE=90°,
∵∠ADB=∠BDE+∠ADE,∠ADC=∠CDE﹣∠ADE,
∴∠ADB﹣∠ADC=2∠ADE,
∴∠C﹣∠B=2∠ADE.
(2)解:结论:∠AMF﹣∠ANF=2∠DAF.
理由:如图2中,作DE∥AF交AB于E.
∵∠AMF=∠MFC+∠C,∠ANF=∠B+∠BFN,∠MFC=∠NFB=α,
∴∠AMF﹣∠ANF=(∠MFC+∠C)﹣(∠B+∠NFB)=∠C﹣∠B,
由(1)可知∠C﹣∠B=2∠ADE,
∵DE∥AF,
∴∠ADE=∠DAF,
∴∠AMF﹣∠ANF=2∠DAF.
25.解:∵将△ABP绕点A逆时针旋转后能与△ACP′重合,
∴△ABP≌△ACP′,
∴AP=AP′=3,∠BAP=∠CAP′,
∵∠BAC=90°,
∴∠BAP+∠CAP=90°,
∴∠CAP′+∠CAP=90°,
即∠PAP′=90°,
∴△PAP′是等腰直角三角形,
由勾股定理得:PP′==3,
即PP′的长是3.
26.(1)证明:∵将△ABC绕点C顺时针旋转60°得到△DEC,
∴∠BCE=∠ACD=60°,CB=CE,
∴△BCE是等边三角形;
(2)DF=BE.
证明:连接BF,
∵点F是边AC中点,
∴CF=BF=AF=AC,
∵∠A=60°,
∴∠BCA=30°,
∴BA=AC,
∴BF=AB=AF=CF,
∵将△ABC绕点C顺时针旋转60°,点A、B的对应点分别为D、E.
∴AB=DE,
∴DE=BF.
延长BF交CE于点G,则∠BGE=∠GBC+∠BCG=90°,
∴∠BGE=∠DEC,
∴BF∥ED,
∴四边形BEDF是平行四边形,
∴DF=BE.
27.(1)证明:∵将△ABD绕点A逆时针旋转60°得△ACE
∴△ABD≌△ACE,∠BAC=∠DAE,
∴AD=AE,BD=CE,∠AEC=∠ADB=120°,
∵△ABC为等边三角形
∴∠BAC=60°
∴∠DAE=60°
∴△ADE为等边三角形,
∴AD=DE,
(2)∠ADC=90°,∠AEC=120°,∠DAE=60°
∴∠DCE=360°﹣∠ADC﹣∠AEC﹣∠DAE=90°,
(3)∵△ADE为等边三角形
∴∠ADE=60°
∴∠CDE=∠ADC﹣∠ADE=30°
又∵∠DCE=90°
∴DE=2CE=2BD=2,
∴AD=DE=2
在Rt△DCE中,.
28.(1)证明:延长AP交BE于Q,
∵AP平分∠MAB,
∴∠MAP=∠BAP,
∵AM∥BN,
∴∠MAP=∠AQB,
∴∠BAP=∠AQB,
∴AB=BQ,
∵BP平分∠ABE,
∴AP=PQ,
∵AM∥BN,
∴==1,
∴AF=EQ,
∴AB=AF+BE;
(2)①成立,
证明:如图2,
延长AP交BE于Q,
∵AP平分∠MAB,
∴∠MAP=∠BAP,
∵AM∥BN,
∴∠MAP=∠AQB,
∴∠BAP=∠AQB,
∴AB=BQ,
∵BP平分∠ABE,
∴AP=PQ,
∵AM∥BN,
∴==1,
∴AF=EQ,
∴AB=AF+BE;
②不同,猜想:AF+AB=BE,
证明:延长AP交BE于Q,
∵AP平分∠MAB,
∴∠MAP=∠BAP,
∵AM∥BN,
∴∠MAP=∠AQB,
∴∠BAP=∠AQB,
∴AB=BQ,
∵BP平分∠ABE,
∴AP=PQ,
∵AM∥BN,
∴==1,
∴AF=EQ,
∴AF+AB=BE
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
