2020—2021学年人教版数学八年级下册第十六章二次根式——二次根式化简与求值的解题策略及方法(Word版,无答案)
文档属性
| 名称 | 2020—2021学年人教版数学八年级下册第十六章二次根式——二次根式化简与求值的解题策略及方法(Word版,无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 132.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-03 22:02:37 | ||
图片预览



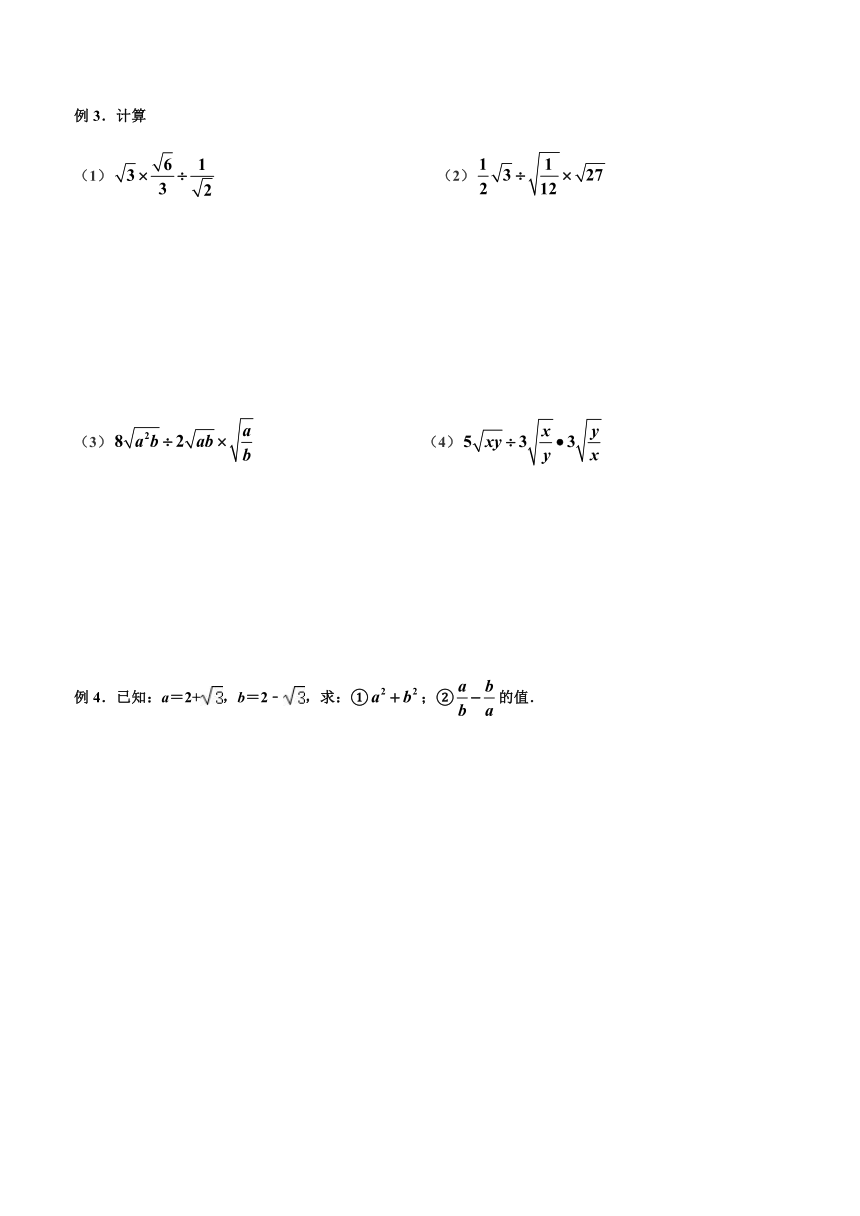
文档简介
二次根式化简与求值的解题策略及方法
【拓展数学思维
提高解题能力】
【知识储备】
(1)二次根式的基本性质:
①≥0;≥0(双重非负性);②(≥0);③(≥0).
(2)二次根式的乘除法公式
①乘法公式:;②除法公式:
(3)二次根式的化简方法:
逆用乘法公式:和除法公式:将二次根式化简,
可以将根号内的平方因式移到根号外.
注意公式:的正确应用.
(4)最简二次根式:我们把满足下满足下列两个条件的二次根式,叫做最简二次根式.
①被开方数不含分母;②被开方数中不含能开得尽方的因数或因式.
(5)分母有理化:把分母中的根号化的过程,叫做分母有理化.
一、基础篇
【例题精讲】
例1.(1)已知实数a,b,c在数轴上的位置如图所示,化简
(2)若2<a<3,则代数式等于(
)
A.5﹣2a
B.1﹣2a
C.2a﹣5
D.2a﹣1
(3)已知a<b,则化简二次根式的正确结果是(
)
A.
B.
C.
D.
(4)已知ab<0,则化简后为(
)
A.
B.﹣a
C.a
D.a
(5)下列二次根式中:①,②,③,④中,⑤,⑥,其中最简二次根式是
(写出序号即可).
例2.填空题:
(1)若y<0,则化成最简二次根式为
.
(2)将根号外面的式子移到根号内是
.
(3)当a<1且a≠0时,化简=
.
例3.计算
(1)
(2)
(3)
(4)
例4.已知:a=2+,b=2﹣,求:①;②的值.
例5.已知x,y为实数,且,求代数式的值.
【课堂练习】
1.已知,那么a的取值范围是(
)
A.a>1
B.a<1
C.a≥1
D.a≤1
2.若a<0,则的值为(
)
A.3
B.﹣3
C.3﹣2a
D.2a﹣3
3.已知a>b,化简二次根式的正确结果是(
)
A.
B.
C.
D.a
4.已知xy>0,化简二次根式的正确结果是(
)
A.
B.
C.
D.
5.已知a=3+,b=3﹣,则代数式的值是(
)
A.24
B.±2
C.2
D.2
6.如图x在数轴上表示数的点的位置,则化简的结果(
)
A.﹣2x
B.-3x
C.2x
D.3x
二、提高篇
例6.将根号外的部分移到根号内
例7.已知:m是的小数部分,求的值.
例8.已知,且x为偶数,求代数式(1+x)的值.
例9.已知x、y为正数,且(+)=3(+5),求的值.
例10.已知:a>0,b>0,,求代数式的值.
【课后作业】
一、选择题
1.下列运算结果正确的是(
)
A.
B.
C.
D.
2.下列根式中,属于最简二次根式的是(
)
A.
B.
C.
D.
3.实数a,b在数轴上的对应点的位置如图所示,下列结论正确的是(
)
A.a>b
B.﹣a<b
C.|﹣a|<|﹣b|
D.
4.若2<a<3,则等于(
)
A.5﹣2a
B.1﹣2a
C.2a﹣5
D.2a﹣1
5.若代数式化简结果为2x﹣3,则x的取值范围是(
)
A.x≤1
B.x≥2
C.x≥1
D.x≥0
二、填空题
6.计算:=
.
7.计算:=
.
8.等式成立的条件是
.
【拓展数学思维
提高解题能力】
【知识储备】
(1)二次根式的基本性质:
①≥0;≥0(双重非负性);②(≥0);③(≥0).
(2)二次根式的乘除法公式
①乘法公式:;②除法公式:
(3)二次根式的化简方法:
逆用乘法公式:和除法公式:将二次根式化简,
可以将根号内的平方因式移到根号外.
注意公式:的正确应用.
(4)最简二次根式:我们把满足下满足下列两个条件的二次根式,叫做最简二次根式.
①被开方数不含分母;②被开方数中不含能开得尽方的因数或因式.
(5)分母有理化:把分母中的根号化的过程,叫做分母有理化.
一、基础篇
【例题精讲】
例1.(1)已知实数a,b,c在数轴上的位置如图所示,化简
(2)若2<a<3,则代数式等于(
)
A.5﹣2a
B.1﹣2a
C.2a﹣5
D.2a﹣1
(3)已知a<b,则化简二次根式的正确结果是(
)
A.
B.
C.
D.
(4)已知ab<0,则化简后为(
)
A.
B.﹣a
C.a
D.a
(5)下列二次根式中:①,②,③,④中,⑤,⑥,其中最简二次根式是
(写出序号即可).
例2.填空题:
(1)若y<0,则化成最简二次根式为
.
(2)将根号外面的式子移到根号内是
.
(3)当a<1且a≠0时,化简=
.
例3.计算
(1)
(2)
(3)
(4)
例4.已知:a=2+,b=2﹣,求:①;②的值.
例5.已知x,y为实数,且,求代数式的值.
【课堂练习】
1.已知,那么a的取值范围是(
)
A.a>1
B.a<1
C.a≥1
D.a≤1
2.若a<0,则的值为(
)
A.3
B.﹣3
C.3﹣2a
D.2a﹣3
3.已知a>b,化简二次根式的正确结果是(
)
A.
B.
C.
D.a
4.已知xy>0,化简二次根式的正确结果是(
)
A.
B.
C.
D.
5.已知a=3+,b=3﹣,则代数式的值是(
)
A.24
B.±2
C.2
D.2
6.如图x在数轴上表示数的点的位置,则化简的结果(
)
A.﹣2x
B.-3x
C.2x
D.3x
二、提高篇
例6.将根号外的部分移到根号内
例7.已知:m是的小数部分,求的值.
例8.已知,且x为偶数,求代数式(1+x)的值.
例9.已知x、y为正数,且(+)=3(+5),求的值.
例10.已知:a>0,b>0,,求代数式的值.
【课后作业】
一、选择题
1.下列运算结果正确的是(
)
A.
B.
C.
D.
2.下列根式中,属于最简二次根式的是(
)
A.
B.
C.
D.
3.实数a,b在数轴上的对应点的位置如图所示,下列结论正确的是(
)
A.a>b
B.﹣a<b
C.|﹣a|<|﹣b|
D.
4.若2<a<3,则等于(
)
A.5﹣2a
B.1﹣2a
C.2a﹣5
D.2a﹣1
5.若代数式化简结果为2x﹣3,则x的取值范围是(
)
A.x≤1
B.x≥2
C.x≥1
D.x≥0
二、填空题
6.计算:=
.
7.计算:=
.
8.等式成立的条件是
.
