2020-2021学年北师大版八年级数学下册课课练1.1.3等腰三角形的判定与反证法(Word版,附答案)
文档属性
| 名称 | 2020-2021学年北师大版八年级数学下册课课练1.1.3等腰三角形的判定与反证法(Word版,附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 439.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-03 00:00:00 | ||
图片预览




文档简介
1 第3课时 等腰三角形的判定与反证法(A卷)
知识点
1 等腰三角形的判定
1.在△ABC中,已知∠B=∠C,则
( )
A.AB=BC
B.AB=AC
C.BC=AC
D.∠A=60°
2.在△ABC中,已知a,b,c分别是∠A,∠B,∠C的对边,则下列条件中,不能判定△ABC是等腰三角形的是
( )
A.a=3,b=3,c=4
B.a∶b∶c=2∶3∶4
C.∠B=50°,∠C=80°
D.∠A∶∠B∶∠C=1∶1∶2
3.如图1-1-26,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,则图中等腰三角形的个数是
( )
A.0
B.1
C.2
D.3
图1-1-26
图1-1-27
4.如图1-1-27,已知OC平分∠AOB,CD∥OB.若OD=3
cm,则CD= cm.?
5.[2020·台州]
如图1-1-28,已知AB=AC,AD=AE,BD和CE相交于点O.
(1)求证:△ABD≌△ACE;
(2)判断△BOC的形状,并说明理由.
图1-1-28
知识点
2 反证法
6.用反证法证明:在一个三角形中不能有两个角是直角,应先设: .?
7.用反证法证明:等腰三角形的两底角必为锐角.
证明:①假设等腰三角形ABC的底角∠B,∠C都是直角,则 ,?
从而 >180°,?
这与 矛盾.?
②假设等腰三角形ABC的底角∠B,∠C都是钝角,
则 ,从而 ,?
这与 矛盾.?
综上所述,假设①② ,?
所以∠B,∠C只能为 .?
故等腰三角形的两底角必为锐角.
8.如图1-1-29,已知:在同一平面内,直线a∥c,b∥c,求证:a∥b.(用反证法证明)
图1-1-29
9.如图1-1-30,∠AOB=60°,OC平分∠AOB,P为射线OC上一点,如果射线OA上的点D满足△OPD是等腰三角形,那么∠ODP的度数为
( )
A.30°
B.120°
C.30°或120°
D.30°或75°或120°
图1-1-30
图1-1-31
10.[教材例2变式]
如图1-1-31,AC,BD相交于点O,∠A=∠D,如果再补充一个条件,使得△BOC是等腰三角形,那么补充的条件不能是( )
A.OA=OD
B.AB=CD
C.∠ABO=∠DCO
D.∠ABC=∠DCB
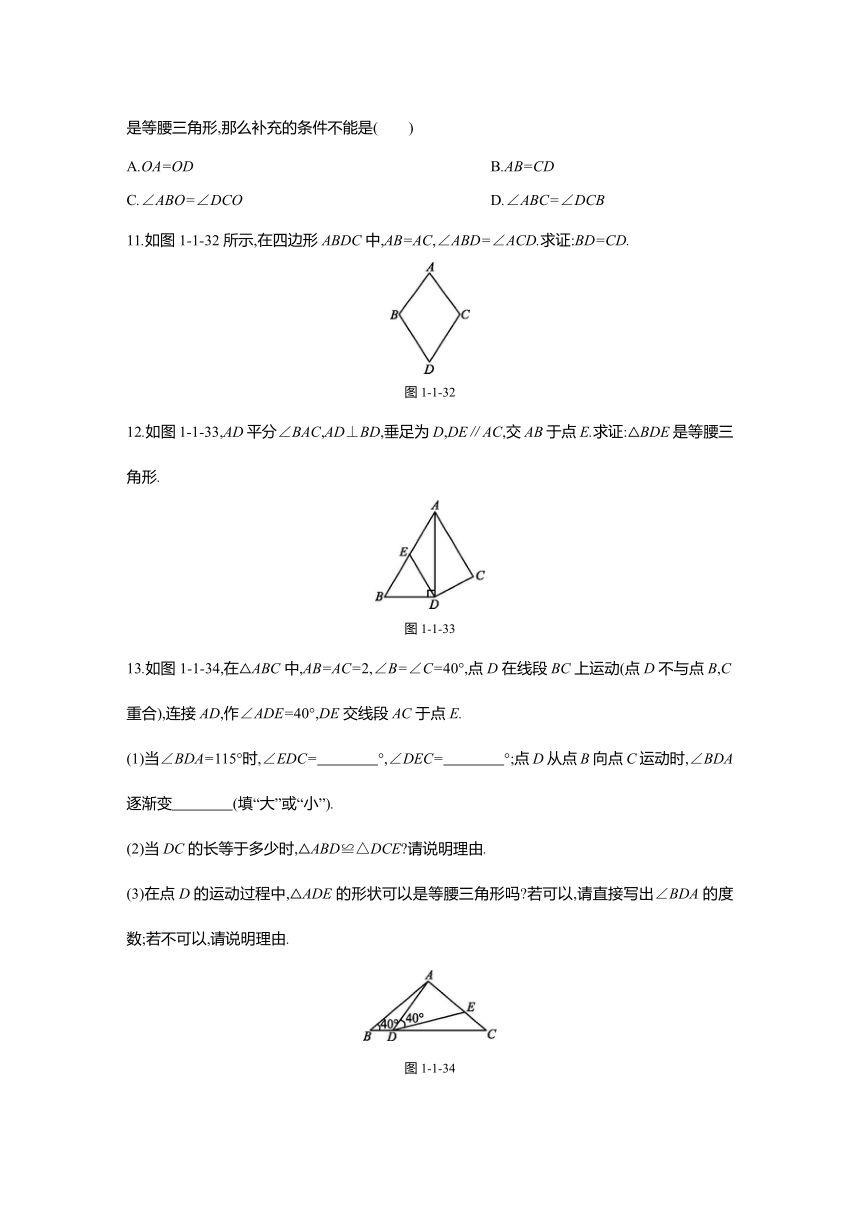
11.如图1-1-32所示,在四边形ABDC中,AB=AC,∠ABD=∠ACD.求证:BD=CD.
图1-1-32
12.如图1-1-33,AD平分∠BAC,AD⊥BD,垂足为D,DE∥AC,交AB于点E.求证:△BDE是等腰三角形.
图1-1-33
13.如图1-1-34,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(点D不与点B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从点B向点C运动时,∠BDA逐渐变 (填“大”或“小”).?
(2)当DC的长等于多少时,△ABD≌△DCE?请说明理由.
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
图1-1-34
(B卷)
命题点
1 判定一个三角形是等腰三角形
1.下列能判定△ABC为等腰三角形的是( )
A.∠A=30°,∠B=60°
B.∠A=50°,∠B=80°
C.AB=AC=2,BC=4
D.AB=3,BC=7,周长为13
2.以已知线段a,b(a>2b)为边作等腰三角形,则( )
A.只能作以a为腰的等腰三角形
B.只能作以b为腰的等腰三角形
C.可以分别以a,b为腰作等腰三角形
D.不能作符合条件的等腰三角形
3.2019·上海奉贤模拟
如图1-1-22,已知△ABC,点D,E分别在边AC,AB上,∠ABD=∠ACE,下列条件中,不能判定△ABC是等腰三角形的是( )
图1-1-22
A.AE=AD
B.BD=CE
C.∠ECB=∠DBC
D.∠BEC=∠CDB
4.小明在证明“有两个角相等的三角形是等腰三角形”这一命题时,画出了图形(如图1-1-23),并写出了“已知”“求证”,他对辅助线的描述如下:“过点A作BC的中垂线AD,垂足为D”.
已知:如图1-1-23,在△ABC中,∠B=∠C.
求证:AB=AC.
(1)请你简要说明小明的辅助线作法错在哪里?
(2)请你正确完整地写出这一命题的证明过程.
图1-1-23
5.如图1-1-24,从①∠B=∠C;②∠BAD=∠CDA;③AB=DC;④BE=CE四个等式中选出两个作为条件,证明△AED是等腰三角形(写出一种即可).
已知:________(只填序号).
求证:△AED是等腰三角形.
证明:
图1-1-24
命题点
2 等腰三角形判定的应用
6.如图1-1-25,在△ABC中,∠ABC和∠ACB的平分线相交于点P,过点P作DE∥BC交AB于点D,交AC于点E,若BD=5,CE=4,则DE的长为________.
7.如图1-1-26,在△ABC中,AB=AC,点E在边CA的延长线上,EP⊥BC于点P,交AB于点F.若AF=2,BF=3,则CE的长为________.
图1-1-26
8.图1-1-27是一座斜拉桥的剖面图.BC是桥面,AD是桥墩,设计大桥时工程师要求斜拉的钢绳AB等于AC.大桥建成后,工程技术人员要对大桥质量进行验收,由于桥墩AD很高,无法直接测量钢绳AB,AC的长度,请你用两种方法检验AB,AC的长度是否相等.(检验工具为刻度尺、量角器.检验时,人只能站在桥面上)
图1-1-27
命题点
3 反证法
9.用反证法证明命题“三角形中至少有一个内角小于或等于60°”时,首先应假设这个三角形中( )
A.有一个内角大于60°
B.有一个内角小于60°
C.每一个内角都大于60°
D.每一个内角都小于60°
10.2020·宁波奉化区期中
用反证法证明等腰三角形的两个底角必为锐角.
11.如图1-1-28,已知P是射线BM上一动点(点P不与点B重合),O是射线BM反向延长线上的一点,∠AOB=30°,∠ABM=60°,当∠OAP的度数为____________时,以A,O,B中的两点和点P为顶点的三角形是等腰三角形.
图1-1-28
12.如图1-1-29(a)所示,在△ABC中,AB=AC,∠A=36°.
(1)求∠ABC的度数.
(2)如图(b)所示,BD是△ABC的角平分线.
①找出图中所有的等腰三角形(等腰三角形ABC除外),并选择其中一个写出推理过程.
②在直线BC上是否存在点P,使△CDP是以CD为一腰的等腰三角形?如果存在,请在图(c)中画出所有满足条件的点P,并直接写出相应的∠CPD的度数;如果不存在,请说明理由.
教师详解详析
1.B
2.B
3.D [解析]
∵AB=AC,∴△ABC为等腰三角形,∠ABC=∠C=(180°-∠A)=(180°-36°)=72°.
∵BD平分∠ABC,
∴∠ABD=∠CBD=×72°=36°,
∴∠ABD=∠A,
∴△ABD为等腰三角形.
∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴△BDC为等腰三角形.
故选D.
4.3
5.解:(1)证明:在△ABD和△ACE中,
∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS).
(2)△BOC是等腰三角形.
理由如下:
∵△ABD≌△ACE,
∴∠ABD=∠ACE.
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC-∠ABD=∠ACB-∠ACE,
∴∠OBC=∠OCB,
∴BO=CO,
∴△BOC是等腰三角形.
6.在一个三角形中有两个角是直角
7.∠B=∠C=90° ∠A+∠B+∠C 三角形内角和为180° ∠B=∠C>90° ∠A+∠B+∠C>180° 三角形内角和为180° 均不成立 锐角
8.证明:如图.
假设a与b相交,则过点M有两条直线平行于直线c,这与“过直线外一点有且只有一条直线平行于已知直线”相矛盾,所以a∥b.
9.D [解析]
∵∠AOB=60°,OC平分∠AOB,∴∠AOC=30°.如图.①当点D在点D1处时,OD=PD,∴∠AOP=∠OPD=30°,∴∠ODP=180°-30°-30°=120°.②当点D在点D2处时,OP=OD,则∠OPD=∠ODP=(180°-30°)=75°.③当点D在点D3处时,OP=DP,则∠ODP=∠AOP=30°.综上所述,∠ODP的度数为120°或75°或30°.
10.C
11.[解析]
连接BC,利用等角对等边证明.
证明:连接BC.
∵AB=AC,∴∠ABC=∠ACB.
∵∠ABD=∠ACD,
∴∠ABD-∠ABC
=
∠ACD-∠ACB,
即∠DBC=∠DCB,
∴BD=CD.
12.证明:如图.∵DE∥AC,
∴∠1=∠3.
∵AD平分∠BAC,
∴∠1=∠2,∴∠2=∠3.
∵AD⊥BD,
∴∠2+∠B=90°,∠3+∠BDE=90°,
∴∠B=∠BDE,∴BE=DE,
∴△BDE是等腰三角形.
13.解:(1)∠EDC=180°-∠BDA-∠ADE=180°-115°-40°=25°,∠DEC=180°-∠EDC-∠C=180°-25°-40°=115°,点D从点B向点C运动时,∠BDA逐渐变小.
故答案为25,115,小.
(2)当DC=2时,△ABD≌△DCE.理由如下:
∵∠C=40°,∴∠DEC+∠EDC=140°.
∵∠ADE=40°,
∴∠ADB+∠EDC=140°,
∴∠ADB=∠DEC.
又∵AB=DC=2,∠B=∠C,
∴△ABD≌△DCE.
(3)可以.∠BDA的度数为110°或80°.
教师详解详析
1.B
2.A [解析]
∵a>2b,∴不能以线段b为腰作等腰三角形,只能以线段a为腰作等腰三角形.故选A.
3.D [解析]
A.添加AE=AD,可证明△ABD≌△ACE,∴AB=AC,∴△ABC为等腰三角形,故此选项不合题意;B.添加BD=CE,可证△ABD≌△ACE,∴AB=AC,∴△ABC为等腰三角形,故此选项不合题意;C.添加∠ECB=∠DBC,又∵∠ABD=∠ACE,∴∠ABC=∠ACB,∴AB=AC,∴△ABC为等腰三角形,故此选项不合题意;D.添加∠BEC=∠CDB,得不到△ABC为等腰三角形,故此选项符合题意.故选D.
4.解:(1)点A是线段BC外的已知点,过该点只能作线段BC的垂线或中线,但这条垂线是否过中点或中线是否垂直于BC,需要推理证明,不能在作图时同时满足,所以说作BC的中垂线是不对的.
(2)证明:过点A作AD⊥BC于点D,
则∠ADB=∠ADC=90°.
又∵∠B=∠C,AD=AD,
∴△BAD≌△CAD(AAS),
∴AB=AC.
5.解:答案不唯一,如:选择的条件是①②(也可以是①③或①④或②③).
证明:在△BAD和△CDA中,
∵∠B=∠C,∠BAD=∠CDA,AD=DA,
∴△BAD≌△CDA(AAS),
∴∠ADB=∠DAC,即∠ADE=∠DAE,
∴AE=DE,
∴△AED是等腰三角形.
6.9 [解析]
∵BP,CP分别是∠ABC和∠ACB的平分线,
∴∠DBP=∠PBC,∠ECP=∠PCB.
∵DE∥BC,
∴∠DPB=∠PBC,∠EPC=∠PCB,
∴∠DPB=∠DBP,∠ECP=∠EPC,
∴PD=BD,PE=CE.
∵BD=5,CE=4,∴PD=5,PE=4,∴DE=9.
故答案为9.
7.7
8.[解析]
答案不唯一,如(1)根据等腰三角形的判定,测量∠B,∠C的度数即可;
(2)利用线段垂直平分线的性质,测量BD,CD的长度,再测量∠ADB是否等于90°即可.
解:方法一:测量∠B,∠C的度数.若∠B=∠C,则AB=AC(等角对等边).
方法二:测量BD,CD的长度及∠ADB的度数.
若BD=CD,∠ADB=90°,则AB=AC(线段垂直平分线上的点到这条线段两个端点的距离相等).
(其他方法合理也可)
9.C
10.解:已知:△ABC,AB=AC.
求证:∠B,∠C必为锐角.
证明:①假设等腰三角形的底角∠B,∠C都是直角,则∠B+∠C=180°,
所以∠A+∠B+∠C=180°+∠A>180°,这与三角形内角和等于180°矛盾.
②假设等腰三角形的底角∠B,∠C都是钝角,则∠B+∠C>180°,
所以∠A+∠B+∠C>180°,这与三角形内角和等于180°矛盾.
综上所述,假设①②均不成立,
所以∠B,∠C只能为锐角.
故等腰三角形的两个底角必为锐角.
11.75°或120°或90° [解析]
∵点O,B,P在同一条直线上,
∴点O,B,P不能组成三角形,
∴此题分为以下6种情况:
(1)若OA=OP,如图①.
∵∠AOB=30°,OA=OP,
∴∠OAP=∠OPA=×(180°-30°)=75°.
(2)若OA=AP,如图②.
∵∠AOB=30°,OA=AP,
∴∠APO=∠AOB=30°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-30°=120°.
(3)若AP=OP,如图③.
∵∠AOB=30°,AP=OP,
∴∠OAP=∠AOB=30°,
∴∠APM=∠AOB+∠OAP=60°=∠ABM,
此时点B,P重合,不符合题意,舍去.
(4)若AB=AP,如图④.
∵∠ABM=60°,AB=AP,
∴∠APO=∠ABM=60°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-60°=90°.
(5)若AB=BP,如图⑤.
∵∠ABM=60°,AB=BP,
∴∠BAP=∠APO=×(180°-60°)=60°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-60°=90°.
(6)若AP=BP,如图⑥.
∵∠ABM=60°,AP=BP,
∴∠PAB=∠ABP=60°,
∴∠APO=180°-60°-60°=60°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-60°=90°.
综上,当∠OAP的度数为75°或120°或90°时,以A,O,B中的两点和点P为顶点的三角形是等腰三角形.故答案为75°或120°或90°.
12.解:(1)∵AB=AC,∠A=36°,
∴∠ABC=∠ACB===72°.
(2)①△ADB,△BCD是等腰三角形.
推理△ADB是等腰三角形的过程如下:
由(1)得∠ABC=72°,
又∵BD是△ABC的角平分线,
∴∠ABD=∠ABC=36°.
又∵∠A=36°,∴∠A=∠ABD,∴AD=BD,
∴△ADB是等腰三角形.
推理△BCD是等腰三角形的过程如下:
由(1)知∠ACB=∠ABC=72°,
又∵BD是△ABC的角平分线,
∴∠DBC=∠ABC=36°,
∴∠BDC=180°-∠ACB-∠DBC=180°-72°-36°=72°,
∴∠ACB=∠BDC,
∴BD=BC,∴△BCD是等腰三角形.
②存在3个点P,使△CDP是以CD为一腰的等腰三角形.若∠CDP为顶角,CD为一腰,则∠CPD=72°(如图甲所示);若∠DCP为顶角,CD为一腰,则存在两个点P:一点在线段BC的延长线上,此时∠CPD=36°(如图乙所示),一点在线段BC上,此时∠CPD=54°(如图丙所示).
知识点
1 等腰三角形的判定
1.在△ABC中,已知∠B=∠C,则
( )
A.AB=BC
B.AB=AC
C.BC=AC
D.∠A=60°
2.在△ABC中,已知a,b,c分别是∠A,∠B,∠C的对边,则下列条件中,不能判定△ABC是等腰三角形的是
( )
A.a=3,b=3,c=4
B.a∶b∶c=2∶3∶4
C.∠B=50°,∠C=80°
D.∠A∶∠B∶∠C=1∶1∶2
3.如图1-1-26,在△ABC中,∠A=36°,AB=AC,BD平分∠ABC交AC于点D,则图中等腰三角形的个数是
( )
A.0
B.1
C.2
D.3
图1-1-26
图1-1-27
4.如图1-1-27,已知OC平分∠AOB,CD∥OB.若OD=3
cm,则CD= cm.?
5.[2020·台州]
如图1-1-28,已知AB=AC,AD=AE,BD和CE相交于点O.
(1)求证:△ABD≌△ACE;
(2)判断△BOC的形状,并说明理由.
图1-1-28
知识点
2 反证法
6.用反证法证明:在一个三角形中不能有两个角是直角,应先设: .?
7.用反证法证明:等腰三角形的两底角必为锐角.
证明:①假设等腰三角形ABC的底角∠B,∠C都是直角,则 ,?
从而 >180°,?
这与 矛盾.?
②假设等腰三角形ABC的底角∠B,∠C都是钝角,
则 ,从而 ,?
这与 矛盾.?
综上所述,假设①② ,?
所以∠B,∠C只能为 .?
故等腰三角形的两底角必为锐角.
8.如图1-1-29,已知:在同一平面内,直线a∥c,b∥c,求证:a∥b.(用反证法证明)
图1-1-29
9.如图1-1-30,∠AOB=60°,OC平分∠AOB,P为射线OC上一点,如果射线OA上的点D满足△OPD是等腰三角形,那么∠ODP的度数为
( )
A.30°
B.120°
C.30°或120°
D.30°或75°或120°
图1-1-30
图1-1-31
10.[教材例2变式]
如图1-1-31,AC,BD相交于点O,∠A=∠D,如果再补充一个条件,使得△BOC是等腰三角形,那么补充的条件不能是( )
A.OA=OD
B.AB=CD
C.∠ABO=∠DCO
D.∠ABC=∠DCB
11.如图1-1-32所示,在四边形ABDC中,AB=AC,∠ABD=∠ACD.求证:BD=CD.
图1-1-32
12.如图1-1-33,AD平分∠BAC,AD⊥BD,垂足为D,DE∥AC,交AB于点E.求证:△BDE是等腰三角形.
图1-1-33
13.如图1-1-34,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(点D不与点B,C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从点B向点C运动时,∠BDA逐渐变 (填“大”或“小”).?
(2)当DC的长等于多少时,△ABD≌△DCE?请说明理由.
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数;若不可以,请说明理由.
图1-1-34
(B卷)
命题点
1 判定一个三角形是等腰三角形
1.下列能判定△ABC为等腰三角形的是( )
A.∠A=30°,∠B=60°
B.∠A=50°,∠B=80°
C.AB=AC=2,BC=4
D.AB=3,BC=7,周长为13
2.以已知线段a,b(a>2b)为边作等腰三角形,则( )
A.只能作以a为腰的等腰三角形
B.只能作以b为腰的等腰三角形
C.可以分别以a,b为腰作等腰三角形
D.不能作符合条件的等腰三角形
3.2019·上海奉贤模拟
如图1-1-22,已知△ABC,点D,E分别在边AC,AB上,∠ABD=∠ACE,下列条件中,不能判定△ABC是等腰三角形的是( )
图1-1-22
A.AE=AD
B.BD=CE
C.∠ECB=∠DBC
D.∠BEC=∠CDB
4.小明在证明“有两个角相等的三角形是等腰三角形”这一命题时,画出了图形(如图1-1-23),并写出了“已知”“求证”,他对辅助线的描述如下:“过点A作BC的中垂线AD,垂足为D”.
已知:如图1-1-23,在△ABC中,∠B=∠C.
求证:AB=AC.
(1)请你简要说明小明的辅助线作法错在哪里?
(2)请你正确完整地写出这一命题的证明过程.
图1-1-23
5.如图1-1-24,从①∠B=∠C;②∠BAD=∠CDA;③AB=DC;④BE=CE四个等式中选出两个作为条件,证明△AED是等腰三角形(写出一种即可).
已知:________(只填序号).
求证:△AED是等腰三角形.
证明:
图1-1-24
命题点
2 等腰三角形判定的应用
6.如图1-1-25,在△ABC中,∠ABC和∠ACB的平分线相交于点P,过点P作DE∥BC交AB于点D,交AC于点E,若BD=5,CE=4,则DE的长为________.
7.如图1-1-26,在△ABC中,AB=AC,点E在边CA的延长线上,EP⊥BC于点P,交AB于点F.若AF=2,BF=3,则CE的长为________.
图1-1-26
8.图1-1-27是一座斜拉桥的剖面图.BC是桥面,AD是桥墩,设计大桥时工程师要求斜拉的钢绳AB等于AC.大桥建成后,工程技术人员要对大桥质量进行验收,由于桥墩AD很高,无法直接测量钢绳AB,AC的长度,请你用两种方法检验AB,AC的长度是否相等.(检验工具为刻度尺、量角器.检验时,人只能站在桥面上)
图1-1-27
命题点
3 反证法
9.用反证法证明命题“三角形中至少有一个内角小于或等于60°”时,首先应假设这个三角形中( )
A.有一个内角大于60°
B.有一个内角小于60°
C.每一个内角都大于60°
D.每一个内角都小于60°
10.2020·宁波奉化区期中
用反证法证明等腰三角形的两个底角必为锐角.
11.如图1-1-28,已知P是射线BM上一动点(点P不与点B重合),O是射线BM反向延长线上的一点,∠AOB=30°,∠ABM=60°,当∠OAP的度数为____________时,以A,O,B中的两点和点P为顶点的三角形是等腰三角形.
图1-1-28
12.如图1-1-29(a)所示,在△ABC中,AB=AC,∠A=36°.
(1)求∠ABC的度数.
(2)如图(b)所示,BD是△ABC的角平分线.
①找出图中所有的等腰三角形(等腰三角形ABC除外),并选择其中一个写出推理过程.
②在直线BC上是否存在点P,使△CDP是以CD为一腰的等腰三角形?如果存在,请在图(c)中画出所有满足条件的点P,并直接写出相应的∠CPD的度数;如果不存在,请说明理由.
教师详解详析
1.B
2.B
3.D [解析]
∵AB=AC,∴△ABC为等腰三角形,∠ABC=∠C=(180°-∠A)=(180°-36°)=72°.
∵BD平分∠ABC,
∴∠ABD=∠CBD=×72°=36°,
∴∠ABD=∠A,
∴△ABD为等腰三角形.
∵∠BDC=∠A+∠ABD=72°,
∴∠BDC=∠C,
∴△BDC为等腰三角形.
故选D.
4.3
5.解:(1)证明:在△ABD和△ACE中,
∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS).
(2)△BOC是等腰三角形.
理由如下:
∵△ABD≌△ACE,
∴∠ABD=∠ACE.
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC-∠ABD=∠ACB-∠ACE,
∴∠OBC=∠OCB,
∴BO=CO,
∴△BOC是等腰三角形.
6.在一个三角形中有两个角是直角
7.∠B=∠C=90° ∠A+∠B+∠C 三角形内角和为180° ∠B=∠C>90° ∠A+∠B+∠C>180° 三角形内角和为180° 均不成立 锐角
8.证明:如图.
假设a与b相交,则过点M有两条直线平行于直线c,这与“过直线外一点有且只有一条直线平行于已知直线”相矛盾,所以a∥b.
9.D [解析]
∵∠AOB=60°,OC平分∠AOB,∴∠AOC=30°.如图.①当点D在点D1处时,OD=PD,∴∠AOP=∠OPD=30°,∴∠ODP=180°-30°-30°=120°.②当点D在点D2处时,OP=OD,则∠OPD=∠ODP=(180°-30°)=75°.③当点D在点D3处时,OP=DP,则∠ODP=∠AOP=30°.综上所述,∠ODP的度数为120°或75°或30°.
10.C
11.[解析]
连接BC,利用等角对等边证明.
证明:连接BC.
∵AB=AC,∴∠ABC=∠ACB.
∵∠ABD=∠ACD,
∴∠ABD-∠ABC
=
∠ACD-∠ACB,
即∠DBC=∠DCB,
∴BD=CD.
12.证明:如图.∵DE∥AC,
∴∠1=∠3.
∵AD平分∠BAC,
∴∠1=∠2,∴∠2=∠3.
∵AD⊥BD,
∴∠2+∠B=90°,∠3+∠BDE=90°,
∴∠B=∠BDE,∴BE=DE,
∴△BDE是等腰三角形.
13.解:(1)∠EDC=180°-∠BDA-∠ADE=180°-115°-40°=25°,∠DEC=180°-∠EDC-∠C=180°-25°-40°=115°,点D从点B向点C运动时,∠BDA逐渐变小.
故答案为25,115,小.
(2)当DC=2时,△ABD≌△DCE.理由如下:
∵∠C=40°,∴∠DEC+∠EDC=140°.
∵∠ADE=40°,
∴∠ADB+∠EDC=140°,
∴∠ADB=∠DEC.
又∵AB=DC=2,∠B=∠C,
∴△ABD≌△DCE.
(3)可以.∠BDA的度数为110°或80°.
教师详解详析
1.B
2.A [解析]
∵a>2b,∴不能以线段b为腰作等腰三角形,只能以线段a为腰作等腰三角形.故选A.
3.D [解析]
A.添加AE=AD,可证明△ABD≌△ACE,∴AB=AC,∴△ABC为等腰三角形,故此选项不合题意;B.添加BD=CE,可证△ABD≌△ACE,∴AB=AC,∴△ABC为等腰三角形,故此选项不合题意;C.添加∠ECB=∠DBC,又∵∠ABD=∠ACE,∴∠ABC=∠ACB,∴AB=AC,∴△ABC为等腰三角形,故此选项不合题意;D.添加∠BEC=∠CDB,得不到△ABC为等腰三角形,故此选项符合题意.故选D.
4.解:(1)点A是线段BC外的已知点,过该点只能作线段BC的垂线或中线,但这条垂线是否过中点或中线是否垂直于BC,需要推理证明,不能在作图时同时满足,所以说作BC的中垂线是不对的.
(2)证明:过点A作AD⊥BC于点D,
则∠ADB=∠ADC=90°.
又∵∠B=∠C,AD=AD,
∴△BAD≌△CAD(AAS),
∴AB=AC.
5.解:答案不唯一,如:选择的条件是①②(也可以是①③或①④或②③).
证明:在△BAD和△CDA中,
∵∠B=∠C,∠BAD=∠CDA,AD=DA,
∴△BAD≌△CDA(AAS),
∴∠ADB=∠DAC,即∠ADE=∠DAE,
∴AE=DE,
∴△AED是等腰三角形.
6.9 [解析]
∵BP,CP分别是∠ABC和∠ACB的平分线,
∴∠DBP=∠PBC,∠ECP=∠PCB.
∵DE∥BC,
∴∠DPB=∠PBC,∠EPC=∠PCB,
∴∠DPB=∠DBP,∠ECP=∠EPC,
∴PD=BD,PE=CE.
∵BD=5,CE=4,∴PD=5,PE=4,∴DE=9.
故答案为9.
7.7
8.[解析]
答案不唯一,如(1)根据等腰三角形的判定,测量∠B,∠C的度数即可;
(2)利用线段垂直平分线的性质,测量BD,CD的长度,再测量∠ADB是否等于90°即可.
解:方法一:测量∠B,∠C的度数.若∠B=∠C,则AB=AC(等角对等边).
方法二:测量BD,CD的长度及∠ADB的度数.
若BD=CD,∠ADB=90°,则AB=AC(线段垂直平分线上的点到这条线段两个端点的距离相等).
(其他方法合理也可)
9.C
10.解:已知:△ABC,AB=AC.
求证:∠B,∠C必为锐角.
证明:①假设等腰三角形的底角∠B,∠C都是直角,则∠B+∠C=180°,
所以∠A+∠B+∠C=180°+∠A>180°,这与三角形内角和等于180°矛盾.
②假设等腰三角形的底角∠B,∠C都是钝角,则∠B+∠C>180°,
所以∠A+∠B+∠C>180°,这与三角形内角和等于180°矛盾.
综上所述,假设①②均不成立,
所以∠B,∠C只能为锐角.
故等腰三角形的两个底角必为锐角.
11.75°或120°或90° [解析]
∵点O,B,P在同一条直线上,
∴点O,B,P不能组成三角形,
∴此题分为以下6种情况:
(1)若OA=OP,如图①.
∵∠AOB=30°,OA=OP,
∴∠OAP=∠OPA=×(180°-30°)=75°.
(2)若OA=AP,如图②.
∵∠AOB=30°,OA=AP,
∴∠APO=∠AOB=30°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-30°=120°.
(3)若AP=OP,如图③.
∵∠AOB=30°,AP=OP,
∴∠OAP=∠AOB=30°,
∴∠APM=∠AOB+∠OAP=60°=∠ABM,
此时点B,P重合,不符合题意,舍去.
(4)若AB=AP,如图④.
∵∠ABM=60°,AB=AP,
∴∠APO=∠ABM=60°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-60°=90°.
(5)若AB=BP,如图⑤.
∵∠ABM=60°,AB=BP,
∴∠BAP=∠APO=×(180°-60°)=60°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-60°=90°.
(6)若AP=BP,如图⑥.
∵∠ABM=60°,AP=BP,
∴∠PAB=∠ABP=60°,
∴∠APO=180°-60°-60°=60°,
∴∠OAP=180°-∠AOB-∠APO=180°-30°-60°=90°.
综上,当∠OAP的度数为75°或120°或90°时,以A,O,B中的两点和点P为顶点的三角形是等腰三角形.故答案为75°或120°或90°.
12.解:(1)∵AB=AC,∠A=36°,
∴∠ABC=∠ACB===72°.
(2)①△ADB,△BCD是等腰三角形.
推理△ADB是等腰三角形的过程如下:
由(1)得∠ABC=72°,
又∵BD是△ABC的角平分线,
∴∠ABD=∠ABC=36°.
又∵∠A=36°,∴∠A=∠ABD,∴AD=BD,
∴△ADB是等腰三角形.
推理△BCD是等腰三角形的过程如下:
由(1)知∠ACB=∠ABC=72°,
又∵BD是△ABC的角平分线,
∴∠DBC=∠ABC=36°,
∴∠BDC=180°-∠ACB-∠DBC=180°-72°-36°=72°,
∴∠ACB=∠BDC,
∴BD=BC,∴△BCD是等腰三角形.
②存在3个点P,使△CDP是以CD为一腰的等腰三角形.若∠CDP为顶角,CD为一腰,则∠CPD=72°(如图甲所示);若∠DCP为顶角,CD为一腰,则存在两个点P:一点在线段BC的延长线上,此时∠CPD=36°(如图乙所示),一点在线段BC上,此时∠CPD=54°(如图丙所示).
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
