2020-2021学年八年级数学北师大版下册课课练2.5.1一元一次不等式与一次函数的关系(Word版,附答案)
文档属性
| 名称 | 2020-2021学年八年级数学北师大版下册课课练2.5.1一元一次不等式与一次函数的关系(Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 349.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-03 22:24:07 | ||
图片预览


文档简介
5 第1课时 一元一次不等式与一次函数的关系
(A卷)
知识点 一元一次不等式与一次函数的关系
1.如图2-5-1,若一次函数y=kx+b的图象与两坐标轴分别交于A,B两点,点A的坐标为(0,3),点B的坐标为(3,0),则关于x的不等式kx+b>0的解集为
( )
A.x>
B.x<
C.x>3
D.x<3
2.如图2-5-2,一次函数y=kx+b的图象经过点A(-2,4),则关于x的不等式kx+b>4的解集为
( )
A.x>-2
B.x<-2
C.x>4
D.x<4
图2-5-2
图2-5-3
3.[教材习题2.6第1题变式]
如图2-5-3,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集在数轴上的表示正确的是
( )
图2-5-4
4.如图2-5-5,甲、乙两名学生均沿同一方向在同一直线上行进,OA,BA分别表示甲、乙两名学生运动过程中离出发点的距离s(m)与时间t(s)之间的函数关系图象.试根据图象回答下列问题:
(1)甲、乙两名学生中,谁的速度较快?
(2)在什么时间段内甲在乙的前面?在什么时间段内甲在乙的后面?在什么时间甲、乙二人相遇?
图2-5-5
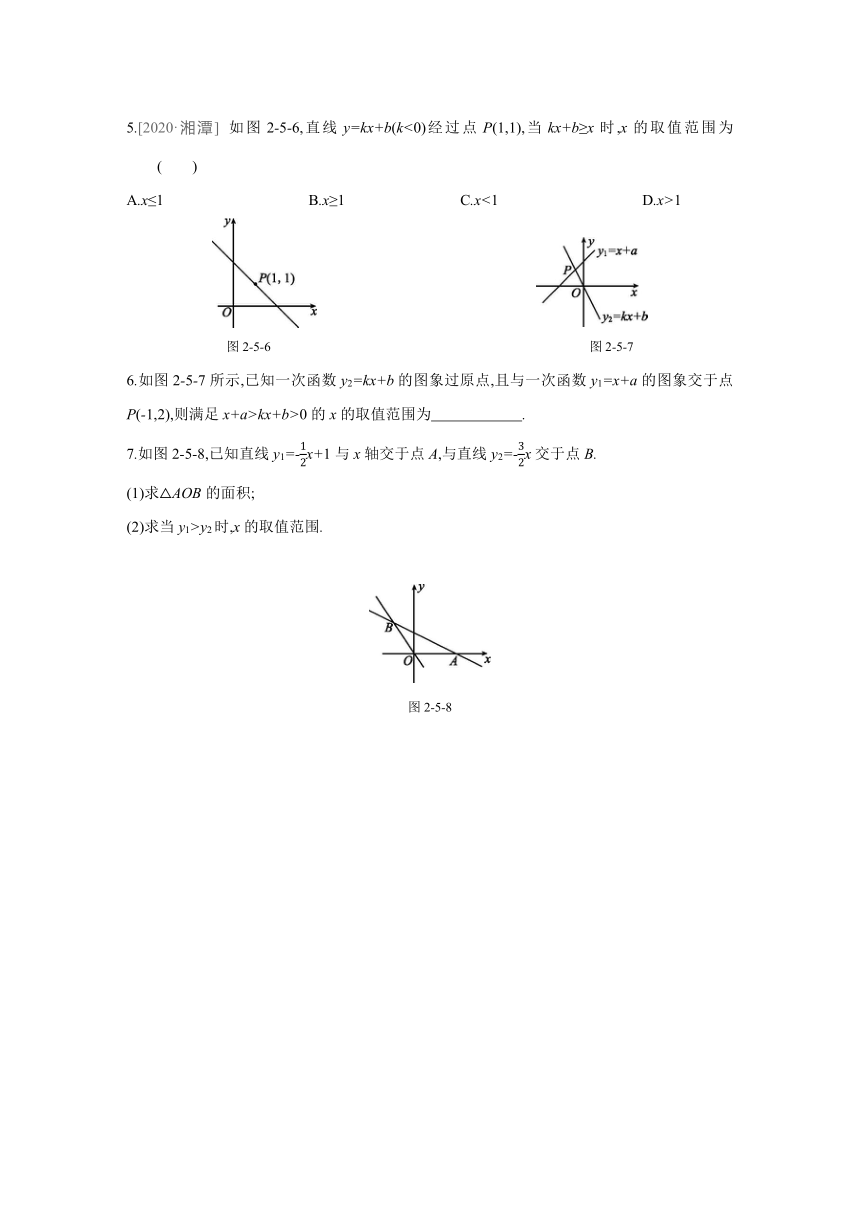
5.[2020·湘潭]
如图2-5-6,直线y=kx+b(k<0)经过点P(1,1),当kx+b≥x时,x的取值范围为
( )
A.x≤1
B.x≥1
C.x<1
D.x>1
图2-5-6
图2-5-7
6.如图2-5-7所示,已知一次函数y2=kx+b的图象过原点,且与一次函数y1=x+a的图象交于点P(-1,2),则满足x+a>kx+b>0的x的取值范围为 .?
7.如图2-5-8,已知直线y1=-x+1与x轴交于点A,与直线y2=-x交于点B.
(1)求△AOB的面积;
(2)求当y1>y2时,x的取值范围.
图2-5-8
(B卷)
命题点
1 利用一次函数的图象解一元一次不等式
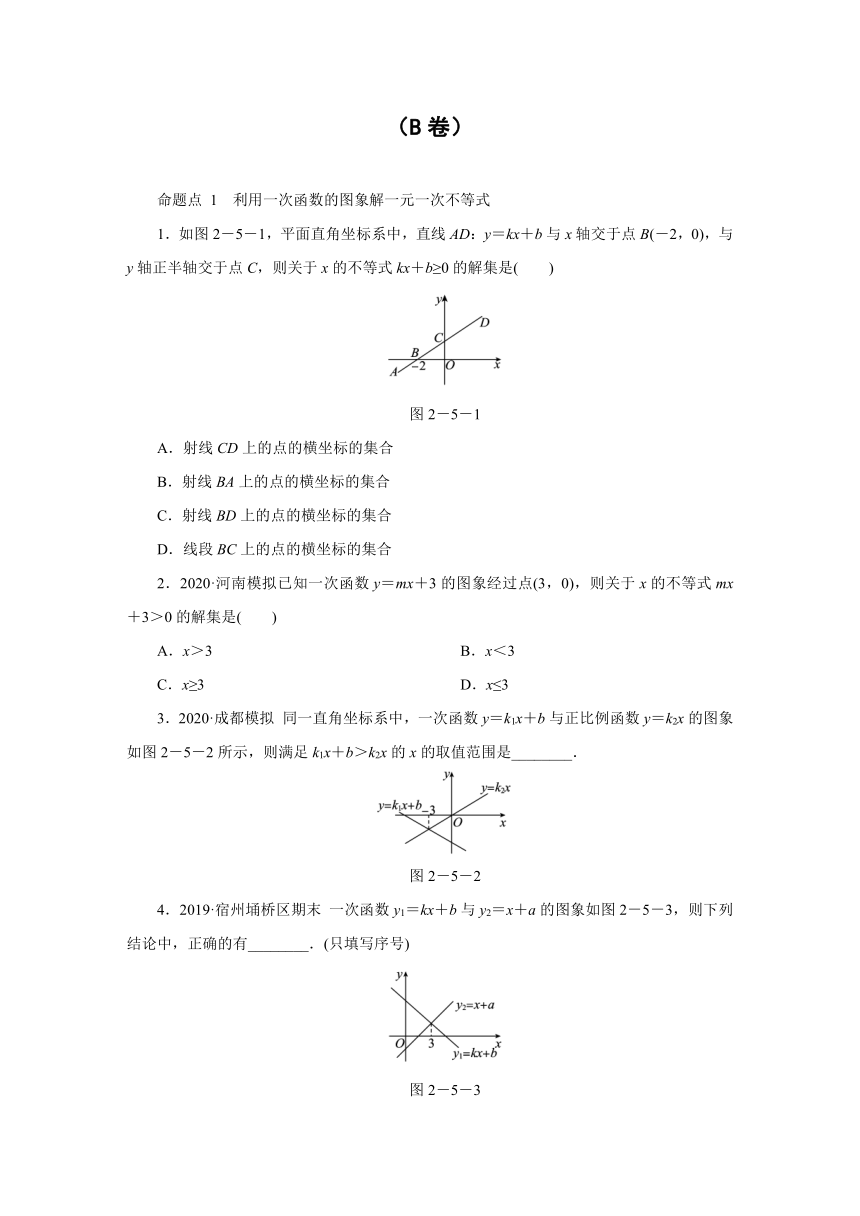
1.如图2-5-1,平面直角坐标系中,直线AD:y=kx+b与x轴交于点B(-2,0),与y轴正半轴交于点C,则关于x的不等式kx+b≥0的解集是( )
图2-5-1
A.射线CD上的点的横坐标的集合
B.射线BA上的点的横坐标的集合
C.射线BD上的点的横坐标的集合
D.线段BC上的点的横坐标的集合
2.2020·河南模拟已知一次函数y=mx+3的图象经过点(3,0),则关于x的不等式mx+3>0的解集是( )
A.x>3
B.x<3
C.x≥3
D.x≤3
3.2020·成都模拟
同一直角坐标系中,一次函数y=k1x+b与正比例函数y=k2x的图象如图2-5-2所示,则满足k1x+b>k2x的x的取值范围是________.
图2-5-2
4.2019·宿州埇桥区期末
一次函数y1=kx+b与y2=x+a的图象如图2-5-3,则下列结论中,正确的有________.(只填写序号)
图2-5-3
①a>0;
②k<0,且y的值随着x值的增大而减小;
③关于x的方程kx+b=x+a的解是x=3;
④当x>3时,y1<y2.
方法点拨(4题)
一元一次不等式与一次函数的关系:
(1)从数的角度来看:求不等式ax+b>cx+d(或ax+b<cx+d)(a≠0,c≠0)的解集,实质上是求当自变量x为何值时,一次函数y=ax+b的值大于(或小于)一次函数y=cx+d的值;
(2)从形的角度来看,求不等式ax+b>cx+d(或ax+b<cx+d)(a≠0,c≠0)的解集,实质上是求直线y=ax+b在直线y=cx+d上方(或下方)时所对应的x的取值范围.
5.2019·滨州
如图2-5-4,直线y=kx+b(k<0)经过点A(3,1),当kx+b<x时,x的取值范围为________.
图2-5-4
6.画出函数y=2x+1的图象,利用图象求:
(1)方程2x+1=0的解;
(2)不等式2x+1≥0的解集;
(3)当y≤3时,x的取值范围;
(4)当-3≤y≤3时,x的取值范围.
7.如图2-5-5,直线l是一次函数y=kx+b的图象,点A,B在直线l上.根据图象回答下列问题:
(1)写出方程kx+b=0的解;
(2)写出不等式kx+b>1的解集;
(3)若直线l上的点P(a,b)在线段AB上移动,求a,b的取值范围.
图2-5-5
命题点
2 利用一元一次不等式与一次函数图象的关系解决实际问题
8.如图2-5-6,l1表示某产品一天的销售收入y1(万元)与销售量x(件)的关系;l2表示该产品一天的销售成本y2(万元)与销售量x(件)的关系.销售收入y1与销售量x之间的函数表达式为________;销售成本y2与销售量x之间的函数表达式为____________;当一天的销售量超过________件时,生产该产品才能获利.(利润=收入-成本)
图2-5-6
9.某单位准备和一个体车主或一国营出租公司中的一家签订月租车合同,设汽车每月行驶x千米,个体车主收费为y1元,国营出租公司收费为y2元,如图2-5-7所示,可知当x________时,选用个体车主比较合算.
图2-5-7
解题突破(9题)
对于图象信息题,了解横、纵坐标表示的意义很重要.该题中,“合算”的意思是选用谁收费低,在图象上如何体现收费的高低?
10.2020·河南模拟
为了积极助力脱贫攻坚工作,如期打赢脱贫攻坚战,某驻村干部带领村民种植草莓,在每年成熟期都会吸引很多人到果园去采摘.现有甲、乙两家果园可供采摘,这两家草莓的品质相同,售价均为每千克30元,但是两家果园的采摘方案不同:
甲果园:每人需购买20元的门票一张,采摘的草莓按6折优惠;
乙果园:不需要购买门票,采摘的草莓按售价付款,没有优惠.
设小明和爸爸、妈妈三个人采摘的草莓数量为x千克,在甲、乙果园采摘所需总费用分别为y甲元,y乙元,其函数图象如图2-5-8所示.
(1)分别写出y甲,y乙与x之间的函数关系式;
(2)请求出图中点A的坐标;
(3)请根据函数图象,直接写出小明一家选择哪家果园采摘更合算.
图2-5-8
11.已知函数y1=x,y2=x+1,y3=-x+5的图象如图2-5-9所示,若无论x取何值,y总取y1,y2,y3中的最小值,求y的最大值.
图2-5-9
教师详解详析
1.D
2.A [解析]
观察图象易知当x>-2时,y>4.
3.C [解析]
不等式x+b>kx+4的解集是一次函数y1=x+b的图象在一次函数y2=kx+4的图象上方时的x的取值范围,故x>1.故选C.
4.解:(1)甲的速度较快.
(2)由图象可看出,在8
s之后,甲在乙的前面,在8
s之前,甲在乙的后面,在8
s时甲、乙二人相遇.
5.A
6.-1当x<0时,y2>0,即kx+b>0;
当函数y1=x+a的图象在函数y2=kx+b的图象的上方时,不等式x+a>kx+b成立,此时x>-1.故答案为-17.解:(1)由y1=-x+1,可知当y1=0时x=2,
所以点A的坐标是(2,0),
所以OA=2.
因为直线y1=-x+1与直线y2=-x交于点B,
所以点B的坐标是(-1,1.5),
所以S△AOB=×2×1.5=1.5.
(2)由(1)可知两直线的交点B的坐标是(-1,1.5),
由函数图象可知当y1>y2时,x的取值范围为x>-1.
教师详解详析
1.C
2.B
3.x<-3
4.②③④
5.x>3 [解析]
∵正比例函数y=x的图象也经过点A,∴kx+b3.
6.解:由题意,得当x=0时,y=1,即函数图象过点(0,1);当y=0时,x=-,即函数图象过点-,0,∴函数图象如图所示.
(1)当x=-时,y=0,
∴方程2x+1=0的解为x=-.
(2)当x≥-时,函数图象在x轴上或x轴的上方,
∴不等式2x+1≥0的解集为x≥-.
(3)当y=3时,x=1,
∴当y≤3时,x的取值范围是x≤1.
(4)当y=-3时,x=-2;当y=3时,x=1,
∴当-3≤y≤3时,x的取值范围是-2≤x≤1.
7.解:直线l与x轴的交点A的坐标为(-2,0),与y轴的交点的坐标为(0,1),且y随x的增大而增大.
(1)∵函数图象经过点(-2,0),
∴方程kx+b=0的解是x=-2.
(2)∵函数图象经过点(0,1),
∴x>0时,有kx+b>1,即不等式kx+b>1的解集是x>0.
(3)∵线段AB对应的自变量的取值范围是-2≤x≤2,
∴-2≤a≤2;
∵当-2≤x≤2时,函数值y的取值范围是0≤y≤2,∴0≤b≤2.
8.y1=x y2=x+2 4 [解析]
设y1=ax,把(4,4)代入,可求得y1=x;设y2=kx+b,把(0,2),(4,4)分别代入,可得y2=x+2.观察图象可发现:当x>4时,y1>y2,即收入>成本.
9.>1500 [解析]
根据图象可以得到当x>1500时,y11500时,选用个体车主比较合算.
10.解:(1)由甲、乙两家果园优惠前的草莓的单价为30元/千克,
可得y甲=18x+60(x≥0).
设y乙=k2x,
根据题意得,10k2=300,
解得k2=30,
∴y乙=30x(x≥0).
(2)联立解得
∴点A的坐标为(5,150).
(3)由图象可得:
当采摘量大于5千克时,到甲家果园采摘更合算;
当采摘量为5千克时,到甲、乙两家果园采摘所需总费用一样;
当采摘量小于5千克时,到乙家果园采摘更合算.
11.解:如图,分别求出三个函数图象交点的坐标A,,B,,C,.
当x<时,y=y1;
当≤x<时,y=y2;
当≤x<时,y=y2;
当x≥时,y=y3.
由图象可得当x=时,y取得最大值,
y最大=.
(A卷)
知识点 一元一次不等式与一次函数的关系
1.如图2-5-1,若一次函数y=kx+b的图象与两坐标轴分别交于A,B两点,点A的坐标为(0,3),点B的坐标为(3,0),则关于x的不等式kx+b>0的解集为
( )
A.x>
B.x<
C.x>3
D.x<3
2.如图2-5-2,一次函数y=kx+b的图象经过点A(-2,4),则关于x的不等式kx+b>4的解集为
( )
A.x>-2
B.x<-2
C.x>4
D.x<4
图2-5-2
图2-5-3
3.[教材习题2.6第1题变式]
如图2-5-3,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),则关于x的不等式x+b>kx+4的解集在数轴上的表示正确的是
( )
图2-5-4
4.如图2-5-5,甲、乙两名学生均沿同一方向在同一直线上行进,OA,BA分别表示甲、乙两名学生运动过程中离出发点的距离s(m)与时间t(s)之间的函数关系图象.试根据图象回答下列问题:
(1)甲、乙两名学生中,谁的速度较快?
(2)在什么时间段内甲在乙的前面?在什么时间段内甲在乙的后面?在什么时间甲、乙二人相遇?
图2-5-5
5.[2020·湘潭]
如图2-5-6,直线y=kx+b(k<0)经过点P(1,1),当kx+b≥x时,x的取值范围为
( )
A.x≤1
B.x≥1
C.x<1
D.x>1
图2-5-6
图2-5-7
6.如图2-5-7所示,已知一次函数y2=kx+b的图象过原点,且与一次函数y1=x+a的图象交于点P(-1,2),则满足x+a>kx+b>0的x的取值范围为 .?
7.如图2-5-8,已知直线y1=-x+1与x轴交于点A,与直线y2=-x交于点B.
(1)求△AOB的面积;
(2)求当y1>y2时,x的取值范围.
图2-5-8
(B卷)
命题点
1 利用一次函数的图象解一元一次不等式
1.如图2-5-1,平面直角坐标系中,直线AD:y=kx+b与x轴交于点B(-2,0),与y轴正半轴交于点C,则关于x的不等式kx+b≥0的解集是( )
图2-5-1
A.射线CD上的点的横坐标的集合
B.射线BA上的点的横坐标的集合
C.射线BD上的点的横坐标的集合
D.线段BC上的点的横坐标的集合
2.2020·河南模拟已知一次函数y=mx+3的图象经过点(3,0),则关于x的不等式mx+3>0的解集是( )
A.x>3
B.x<3
C.x≥3
D.x≤3
3.2020·成都模拟
同一直角坐标系中,一次函数y=k1x+b与正比例函数y=k2x的图象如图2-5-2所示,则满足k1x+b>k2x的x的取值范围是________.
图2-5-2
4.2019·宿州埇桥区期末
一次函数y1=kx+b与y2=x+a的图象如图2-5-3,则下列结论中,正确的有________.(只填写序号)
图2-5-3
①a>0;
②k<0,且y的值随着x值的增大而减小;
③关于x的方程kx+b=x+a的解是x=3;
④当x>3时,y1<y2.
方法点拨(4题)
一元一次不等式与一次函数的关系:
(1)从数的角度来看:求不等式ax+b>cx+d(或ax+b<cx+d)(a≠0,c≠0)的解集,实质上是求当自变量x为何值时,一次函数y=ax+b的值大于(或小于)一次函数y=cx+d的值;
(2)从形的角度来看,求不等式ax+b>cx+d(或ax+b<cx+d)(a≠0,c≠0)的解集,实质上是求直线y=ax+b在直线y=cx+d上方(或下方)时所对应的x的取值范围.
5.2019·滨州
如图2-5-4,直线y=kx+b(k<0)经过点A(3,1),当kx+b<x时,x的取值范围为________.
图2-5-4
6.画出函数y=2x+1的图象,利用图象求:
(1)方程2x+1=0的解;
(2)不等式2x+1≥0的解集;
(3)当y≤3时,x的取值范围;
(4)当-3≤y≤3时,x的取值范围.
7.如图2-5-5,直线l是一次函数y=kx+b的图象,点A,B在直线l上.根据图象回答下列问题:
(1)写出方程kx+b=0的解;
(2)写出不等式kx+b>1的解集;
(3)若直线l上的点P(a,b)在线段AB上移动,求a,b的取值范围.
图2-5-5
命题点
2 利用一元一次不等式与一次函数图象的关系解决实际问题
8.如图2-5-6,l1表示某产品一天的销售收入y1(万元)与销售量x(件)的关系;l2表示该产品一天的销售成本y2(万元)与销售量x(件)的关系.销售收入y1与销售量x之间的函数表达式为________;销售成本y2与销售量x之间的函数表达式为____________;当一天的销售量超过________件时,生产该产品才能获利.(利润=收入-成本)
图2-5-6
9.某单位准备和一个体车主或一国营出租公司中的一家签订月租车合同,设汽车每月行驶x千米,个体车主收费为y1元,国营出租公司收费为y2元,如图2-5-7所示,可知当x________时,选用个体车主比较合算.
图2-5-7
解题突破(9题)
对于图象信息题,了解横、纵坐标表示的意义很重要.该题中,“合算”的意思是选用谁收费低,在图象上如何体现收费的高低?
10.2020·河南模拟
为了积极助力脱贫攻坚工作,如期打赢脱贫攻坚战,某驻村干部带领村民种植草莓,在每年成熟期都会吸引很多人到果园去采摘.现有甲、乙两家果园可供采摘,这两家草莓的品质相同,售价均为每千克30元,但是两家果园的采摘方案不同:
甲果园:每人需购买20元的门票一张,采摘的草莓按6折优惠;
乙果园:不需要购买门票,采摘的草莓按售价付款,没有优惠.
设小明和爸爸、妈妈三个人采摘的草莓数量为x千克,在甲、乙果园采摘所需总费用分别为y甲元,y乙元,其函数图象如图2-5-8所示.
(1)分别写出y甲,y乙与x之间的函数关系式;
(2)请求出图中点A的坐标;
(3)请根据函数图象,直接写出小明一家选择哪家果园采摘更合算.
图2-5-8
11.已知函数y1=x,y2=x+1,y3=-x+5的图象如图2-5-9所示,若无论x取何值,y总取y1,y2,y3中的最小值,求y的最大值.
图2-5-9
教师详解详析
1.D
2.A [解析]
观察图象易知当x>-2时,y>4.
3.C [解析]
不等式x+b>kx+4的解集是一次函数y1=x+b的图象在一次函数y2=kx+4的图象上方时的x的取值范围,故x>1.故选C.
4.解:(1)甲的速度较快.
(2)由图象可看出,在8
s之后,甲在乙的前面,在8
s之前,甲在乙的后面,在8
s时甲、乙二人相遇.
5.A
6.-1
当函数y1=x+a的图象在函数y2=kx+b的图象的上方时,不等式x+a>kx+b成立,此时x>-1.故答案为-1
所以点A的坐标是(2,0),
所以OA=2.
因为直线y1=-x+1与直线y2=-x交于点B,
所以点B的坐标是(-1,1.5),
所以S△AOB=×2×1.5=1.5.
(2)由(1)可知两直线的交点B的坐标是(-1,1.5),
由函数图象可知当y1>y2时,x的取值范围为x>-1.
教师详解详析
1.C
2.B
3.x<-3
4.②③④
5.x>3 [解析]
∵正比例函数y=x的图象也经过点A,∴kx+b
6.解:由题意,得当x=0时,y=1,即函数图象过点(0,1);当y=0时,x=-,即函数图象过点-,0,∴函数图象如图所示.
(1)当x=-时,y=0,
∴方程2x+1=0的解为x=-.
(2)当x≥-时,函数图象在x轴上或x轴的上方,
∴不等式2x+1≥0的解集为x≥-.
(3)当y=3时,x=1,
∴当y≤3时,x的取值范围是x≤1.
(4)当y=-3时,x=-2;当y=3时,x=1,
∴当-3≤y≤3时,x的取值范围是-2≤x≤1.
7.解:直线l与x轴的交点A的坐标为(-2,0),与y轴的交点的坐标为(0,1),且y随x的增大而增大.
(1)∵函数图象经过点(-2,0),
∴方程kx+b=0的解是x=-2.
(2)∵函数图象经过点(0,1),
∴x>0时,有kx+b>1,即不等式kx+b>1的解集是x>0.
(3)∵线段AB对应的自变量的取值范围是-2≤x≤2,
∴-2≤a≤2;
∵当-2≤x≤2时,函数值y的取值范围是0≤y≤2,∴0≤b≤2.
8.y1=x y2=x+2 4 [解析]
设y1=ax,把(4,4)代入,可求得y1=x;设y2=kx+b,把(0,2),(4,4)分别代入,可得y2=x+2.观察图象可发现:当x>4时,y1>y2,即收入>成本.
9.>1500 [解析]
根据图象可以得到当x>1500时,y1
10.解:(1)由甲、乙两家果园优惠前的草莓的单价为30元/千克,
可得y甲=18x+60(x≥0).
设y乙=k2x,
根据题意得,10k2=300,
解得k2=30,
∴y乙=30x(x≥0).
(2)联立解得
∴点A的坐标为(5,150).
(3)由图象可得:
当采摘量大于5千克时,到甲家果园采摘更合算;
当采摘量为5千克时,到甲、乙两家果园采摘所需总费用一样;
当采摘量小于5千克时,到乙家果园采摘更合算.
11.解:如图,分别求出三个函数图象交点的坐标A,,B,,C,.
当x<时,y=y1;
当≤x<时,y=y2;
当≤x<时,y=y2;
当x≥时,y=y3.
由图象可得当x=时,y取得最大值,
y最大=.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
