2020-2021学年八年级数学北师大版下册课课练4.1因式分解 (Word版,附答案)
文档属性
| 名称 | 2020-2021学年八年级数学北师大版下册课课练4.1因式分解 (Word版,附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 283.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-03 22:32:10 | ||
图片预览


文档简介
1 因式分解(A卷)
知识点
1 因式分解的概念
1.下列各式由左到右的变形中,属于因式分解的是( )
A.a(m+n)=am+an
B.a2-b2-c2=(a-b)(a+b)-c2
C.10x2-5x=5x(2x-1)
D.x2-xy+y2=(x-y)2
2.若多项式x2+mx+n因式分解的结果为(x-3)·(x+1),则m,n的值分别为
( )
A.2,3
B.-2,3
C.2,-3
D.-2,-3
3.小明在解答“因式分解:(1)3x2-9x+3;(2)9x2-4.”这道题目时,是这样做的:
解:(1)3x2-9x+3=3(x2-6x+1).
(2)9x2-4=(3x+2)(3x-2).
请你利用因式分解与整式乘法的关系,判断小明分解得对不对.
知识点
2 因式分解的简单应用
4.利用因式分解简便计算57×99+44×99-99,正确的是
( )
A.99×(57+44)=99×101=9999
B.99×(57+44-1)=99×100=9900
C.99×(57+44+1)=99×102=10098
D.99×(57+44-99)=99×2=198
5.如图4-1-1所示,由一个边长为a的小正方形与两个长、宽分别为a,b的小长方形拼接成一个大长方形,则利用整个图形可表示出一些有关多项式因式分解的等式,请你写出任意一个表示因式分解的等式: .?
6.下列各式由左到右的变形中,是因式分解的有 (填序号).?
①3abc3=3c·abc2;②6x2+9x+3=3(2x2+3x);③x2-2=xx-;④x2-2x-1=(x-1)2;⑤4t2-9=(2t+3)(2t-3).
7.[教材习题4.1第4题变式]
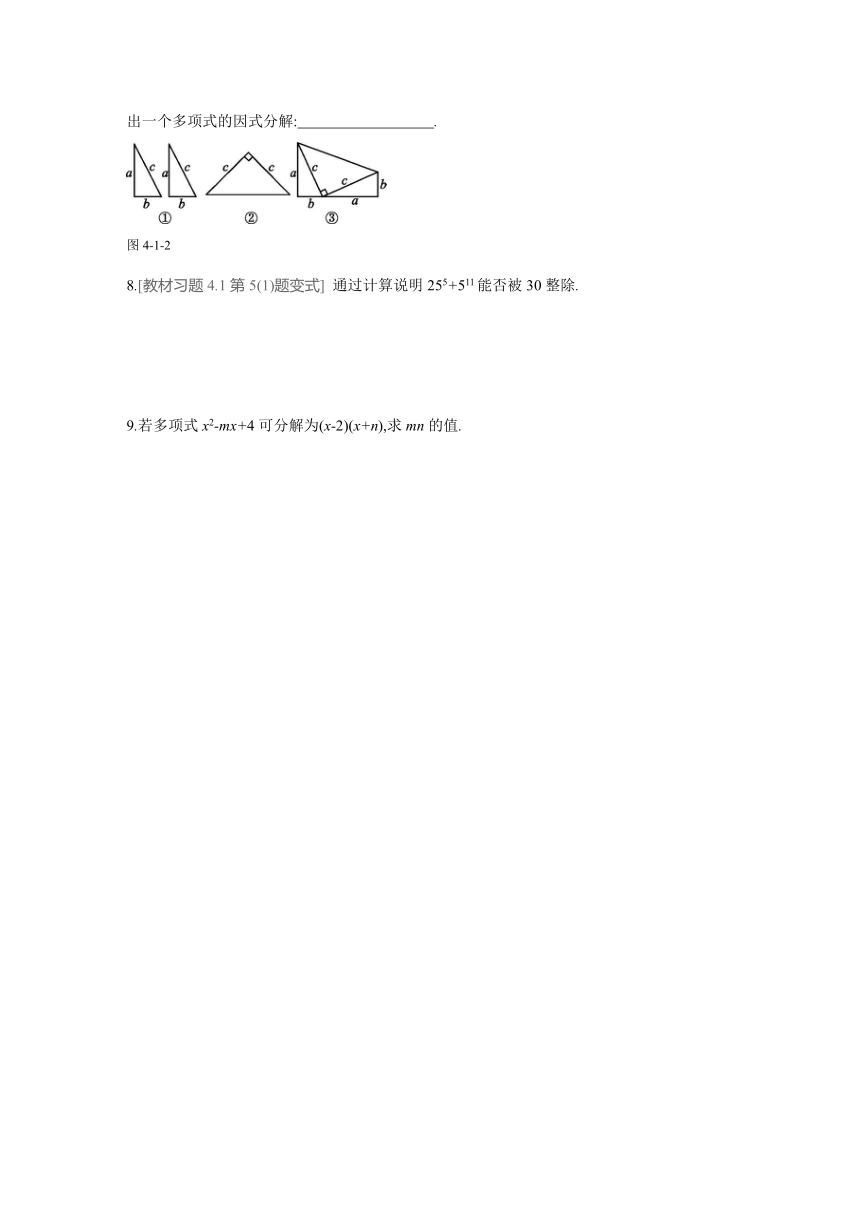
如图4-1-2,将两个全等的直角三角形和一个等腰直角三角形(它的直角边等于前两个直角三角形的斜边)拼接成一个梯形,请根据拼接前后图形面积的关系写出一个多项式的因式分解: .?
图4-1-2
8.[教材习题4.1第5(1)题变式]
通过计算说明255+511能否被30整除.
9.若多项式x2-mx+4可分解为(x-2)(x+n),求mn的值.
(B卷)
命题点
1 因式分解的意义
1.2020·珠海斗门区期末
下列各式从左到右的变形中,属于因式分解的是( )
A.-12x3y=-3x3·4y
B.m(mn-1)=m2n-m
C.y2-4y-1=y(y-4)-1
D.ax+ay=a(x+y)
2.对于下面两个等式:①4a2-8a=4a(a-2);②4a·(a-2)=4a2-8a.其中属于整式乘法的是________,属于因式分解的是________.(填序号)
命题点
2 利用因式分解的意义求字母的值
3.把多项式x2+ax+b因式分解,得(x+1)(x-3),则a,b的值分别是( )
A.2,3
B.-2,-3
C.-2,3
D.2,-3
4.甲、乙两名同学因式分解x2+mx+n,甲看错了n的值,得到的结果为(x+2)(x+6);乙看错了m的值,得到的结果为(x-1)(x-16).请你确定m,n的值.
解题突破(4题)
甲看错了常数项,但二次项系数和一次项系数是正确的;乙看错了一次项系数,但二次项系数和常数项是正确的.
5.2020·西安碑林区月考
阅读材料,并解答问题.
待定系数法:设某一多项式的全部或部分系数为未知数,利用当两个多项式为恒等式时,同类项系数相等的原理确定这些系数,从而得到待求系数的值.待定系数法可以应用到因式分解中,例如:
因式分解:x3-1.
因为x3-1为三次多项式,若能因式分解,则可以分解成一个一次多顶式和一个二次多项式的乘积.故我们可以猜想x3-1=(x-1)(x2+ax+b),展开等式右边得x3+(a-1)x2+(b-a)x-b,根据待定系数法原理,等式两边多项式的同类项的系数相等,得a-1=0,b-a=0,-b=-1,可以求出a=1,b=1.所以x3-1=(x-1)(x2+x+1).
问题:(1)若x取任意值,等式x2+2x+3=x2+(3-a)x+s恒成立,则a=________;
(2)已知多项式x3+2x+3有因式x+1,请用待定系数法求出该多项式的另一个因式.
方法点拨(5题)
用待定系数法因式分解时,可根据条件确定因式中尽量多的系数,减少待定系数的设置.
命题点
3 利用面积相等验证因式分解
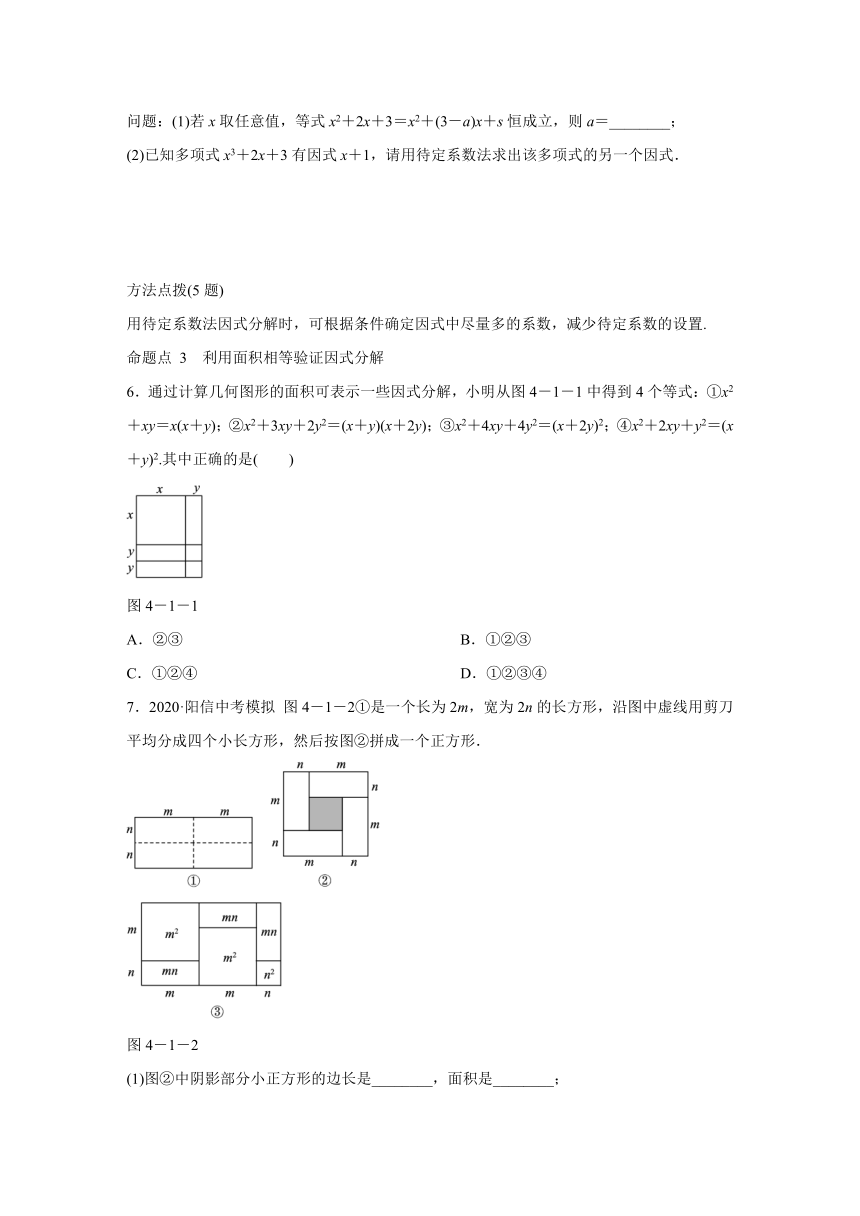
6.通过计算几何图形的面积可表示一些因式分解,小明从图4-1-1中得到4个等式:①x2+xy=x(x+y);②x2+3xy+2y2=(x+y)(x+2y);③x2+4xy+4y2=(x+2y)2;④x2+2xy+y2=(x+y)2.其中正确的是( )
图4-1-1
A.②③
B.①②③
C.①②④
D.①②③④
7.2020·阳信中考模拟
图4-1-2①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四个小长方形,然后按图②拼成一个正方形.
图4-1-2
(1)图②中阴影部分小正方形的边长是________,面积是________;
(2)观察图②,三个代数式(m+n)2,(m-n)2,mn之间的等量关系是________________;
(3)观察图③,你能把2m2+3mn+n2因式分解吗?
8.(1)有若干块长方形和正方形硬纸片如图4-1-3(a)所示,用若干块这样的硬纸片拼成一个新的正方形,如图(b).
①用两种不同的方法,计算图(b)中正方形的面积;
②由此,你可以得出的一个等式为____________.
图4-1-3
(2)有若干块长方形和正方形硬纸片如图(c)所示.
①请你用拼图的方法推导出一个完全平方公式,画出你的拼图;
②请你用拼图的方法推导出2a2+5ab+2b2因式分解的结果,画出你的拼图.
命题点
4 利用因式分解解决计算或整除问题
9.利用简便方法计算:23×2.718+59×2.718+18×2.718.
10.1010-109×8+108×5能被25整除吗?
方法点拨(10题)
要证明一个式子的结果能被一个数整除,一般的方法是将这个式子转化为几个数的乘积的形式,且其中一个因数是这个数.
11.因式分解与整式乘法互为逆变形,请利用a2+ab=a(a+b)解决下列问题:
(1)简便运算:8.72+8.7×1.3;
(2)判断n2+n(n为整数)是奇数还是偶数.
12.发现 任意五个连续整数的平方和是5的倍数.
验证
(1)(-1)2+02+12+22+32的结果是5的几倍?
(2)设五个连续整数的中间数为n,写出它们的平方和,并说明这五个连续整数的平方和是5的倍数.
延伸
任意三个连续整数的平方和被3除的余数是几呢?请说出理由.
教师详解详析
1.C
2.D [解析]
因为(x-3)(x+1)=x2-2x-3,
所以m=-2,n=-3.
3.解:(1)因为3(x2-6x+1)=3x2-18x+3≠3x2-9x+3,
所以小明分解得不对.
(2)因为(3x+2)(3x-2)=(3x)2-4=9x2-4,
所以小明分解得对.
4.B [解析]
逆用乘法对加法的分配律可得原式=99×(57+44-1)=99×100=9900.
5.a2+2ab=a(a+2b)(答案不唯一)
[解析]
把图形分割成一个正方形和两个长方形计算面积,则有a2+2ab=a(a+2b);
把图形分割成两个长方形,一边长分别是a+b,b,另一边长都是a,则有a(a+b)+ab=a(a+2b);
用整个图形的面积减去一个相邻两边长分别为a,a+b的长方形的面积,得到另外一个长方形的面积,这个长方形相邻两边长分别是a,b,即a(a+2b)-a(a+b)=ab.
6.⑤
7.ab+(a2+b2)=(a+b)2
8.解:原式=510+511=510+5×510=6×510=6×5×59=30×59.
因为30×59能被30整除,
所以255+511能被30整除.
9.解:因为x2-mx+4=(x-2)(x+n)=x2+(n-2)x-2n,
所以-m=n-2,-2n=4,
解得m=4,n=-2,
则mn=-8.
教师详解详析
1.D 2.② ①
3.B [解析]
(x+1)(x-3)=x2-2x-3,因此a=-2,b=-3.故选B.
4.解:∵(x+2)(x+6)=x2+8x+12,
∴m=8.
∵(x-1)(x-16)=x2-17x+16,
∴n=16.
5.解:(1)1
(2)设x3+2x+3=(x+1)(x2+ax+3),则x3+2x+3=x3+(a+1)x2+(a+3)x+3,
所以a+1=0,a+3=2,解得a=-1,故该多项式的另一个因式是x2-x+3.
6.C
7.解:(1)m-n (m-n)2
(2)(m+n)2-4mn=(m-n)2
(3)2m2+3mn+n2=(2m+n)(m+n).
8.解:(1)①正方形的面积=a2+2a+1;正方形的面积=(a+1)2.
②a2+2a+1=(a+1)2
(2)①答案不唯一.如图(a)所示,可推导出(a+b)2=a2+2ab+b2.
②如图(b)所示,2a2+5ab+2b2=(2a+b)(a+2b)(拼图不唯一).
9.解:原式=2.718×(23+59+18)=271.8.
10.解:1010-109×8+108×5=108×(102-10×8+5)=25×108,所以原式能被25整除.
11.解:(1)8.72+8.7×1.3=8.7×(8.7+1.3)=8.7×10=87.
(2)n2+n=n(n+1).
若n为奇数,则n+1为偶数;
若n为偶数,则n+1为奇数,
即n与n+1始终一奇一偶,所以n2+n是偶数.
12.解:验证
(1)(-1)2+02+12+22+32=1+0+1+4+9=15,15÷5=3,
即(-1)2+02+12+22+32的结果是5的3倍.
(2)若五个连续整数的中间数为n,则其余的整数是n-2,n-1,n+1,n+2,
它们的平方和为(n-2)2+(n-1)2+n2+(n+1)2+(n+2)2=n2-4n+4+n2-2n+1+n2+n2+2n+1+n2+4n+4=5n2+10.
∵5n2+10=5(n2+2),n是整数,
∴n2+2是整数,
∴这五个连续整数的平方和是5的倍数.
延伸 任意三个连续整数的平方和被3除的余数是2.理由:设三个连续整数的中间数为n,则其余的整数是n-1,n+1,
它们的平方和为(n-1)2+n2+(n+1)2=n2-2n+1+n2+n2+2n+1=3n2+2.
∵n是整数,∴n2是整数.
∵3n2能被3整除,∴3n2+2被3除的余数是2,
即任意三个连续整数的平方和被3除的余数是2.
知识点
1 因式分解的概念
1.下列各式由左到右的变形中,属于因式分解的是( )
A.a(m+n)=am+an
B.a2-b2-c2=(a-b)(a+b)-c2
C.10x2-5x=5x(2x-1)
D.x2-xy+y2=(x-y)2
2.若多项式x2+mx+n因式分解的结果为(x-3)·(x+1),则m,n的值分别为
( )
A.2,3
B.-2,3
C.2,-3
D.-2,-3
3.小明在解答“因式分解:(1)3x2-9x+3;(2)9x2-4.”这道题目时,是这样做的:
解:(1)3x2-9x+3=3(x2-6x+1).
(2)9x2-4=(3x+2)(3x-2).
请你利用因式分解与整式乘法的关系,判断小明分解得对不对.
知识点
2 因式分解的简单应用
4.利用因式分解简便计算57×99+44×99-99,正确的是
( )
A.99×(57+44)=99×101=9999
B.99×(57+44-1)=99×100=9900
C.99×(57+44+1)=99×102=10098
D.99×(57+44-99)=99×2=198
5.如图4-1-1所示,由一个边长为a的小正方形与两个长、宽分别为a,b的小长方形拼接成一个大长方形,则利用整个图形可表示出一些有关多项式因式分解的等式,请你写出任意一个表示因式分解的等式: .?
6.下列各式由左到右的变形中,是因式分解的有 (填序号).?
①3abc3=3c·abc2;②6x2+9x+3=3(2x2+3x);③x2-2=xx-;④x2-2x-1=(x-1)2;⑤4t2-9=(2t+3)(2t-3).
7.[教材习题4.1第4题变式]
如图4-1-2,将两个全等的直角三角形和一个等腰直角三角形(它的直角边等于前两个直角三角形的斜边)拼接成一个梯形,请根据拼接前后图形面积的关系写出一个多项式的因式分解: .?
图4-1-2
8.[教材习题4.1第5(1)题变式]
通过计算说明255+511能否被30整除.
9.若多项式x2-mx+4可分解为(x-2)(x+n),求mn的值.
(B卷)
命题点
1 因式分解的意义
1.2020·珠海斗门区期末
下列各式从左到右的变形中,属于因式分解的是( )
A.-12x3y=-3x3·4y
B.m(mn-1)=m2n-m
C.y2-4y-1=y(y-4)-1
D.ax+ay=a(x+y)
2.对于下面两个等式:①4a2-8a=4a(a-2);②4a·(a-2)=4a2-8a.其中属于整式乘法的是________,属于因式分解的是________.(填序号)
命题点
2 利用因式分解的意义求字母的值
3.把多项式x2+ax+b因式分解,得(x+1)(x-3),则a,b的值分别是( )
A.2,3
B.-2,-3
C.-2,3
D.2,-3
4.甲、乙两名同学因式分解x2+mx+n,甲看错了n的值,得到的结果为(x+2)(x+6);乙看错了m的值,得到的结果为(x-1)(x-16).请你确定m,n的值.
解题突破(4题)
甲看错了常数项,但二次项系数和一次项系数是正确的;乙看错了一次项系数,但二次项系数和常数项是正确的.
5.2020·西安碑林区月考
阅读材料,并解答问题.
待定系数法:设某一多项式的全部或部分系数为未知数,利用当两个多项式为恒等式时,同类项系数相等的原理确定这些系数,从而得到待求系数的值.待定系数法可以应用到因式分解中,例如:
因式分解:x3-1.
因为x3-1为三次多项式,若能因式分解,则可以分解成一个一次多顶式和一个二次多项式的乘积.故我们可以猜想x3-1=(x-1)(x2+ax+b),展开等式右边得x3+(a-1)x2+(b-a)x-b,根据待定系数法原理,等式两边多项式的同类项的系数相等,得a-1=0,b-a=0,-b=-1,可以求出a=1,b=1.所以x3-1=(x-1)(x2+x+1).
问题:(1)若x取任意值,等式x2+2x+3=x2+(3-a)x+s恒成立,则a=________;
(2)已知多项式x3+2x+3有因式x+1,请用待定系数法求出该多项式的另一个因式.
方法点拨(5题)
用待定系数法因式分解时,可根据条件确定因式中尽量多的系数,减少待定系数的设置.
命题点
3 利用面积相等验证因式分解
6.通过计算几何图形的面积可表示一些因式分解,小明从图4-1-1中得到4个等式:①x2+xy=x(x+y);②x2+3xy+2y2=(x+y)(x+2y);③x2+4xy+4y2=(x+2y)2;④x2+2xy+y2=(x+y)2.其中正确的是( )
图4-1-1
A.②③
B.①②③
C.①②④
D.①②③④
7.2020·阳信中考模拟
图4-1-2①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四个小长方形,然后按图②拼成一个正方形.
图4-1-2
(1)图②中阴影部分小正方形的边长是________,面积是________;
(2)观察图②,三个代数式(m+n)2,(m-n)2,mn之间的等量关系是________________;
(3)观察图③,你能把2m2+3mn+n2因式分解吗?
8.(1)有若干块长方形和正方形硬纸片如图4-1-3(a)所示,用若干块这样的硬纸片拼成一个新的正方形,如图(b).
①用两种不同的方法,计算图(b)中正方形的面积;
②由此,你可以得出的一个等式为____________.
图4-1-3
(2)有若干块长方形和正方形硬纸片如图(c)所示.
①请你用拼图的方法推导出一个完全平方公式,画出你的拼图;
②请你用拼图的方法推导出2a2+5ab+2b2因式分解的结果,画出你的拼图.
命题点
4 利用因式分解解决计算或整除问题
9.利用简便方法计算:23×2.718+59×2.718+18×2.718.
10.1010-109×8+108×5能被25整除吗?
方法点拨(10题)
要证明一个式子的结果能被一个数整除,一般的方法是将这个式子转化为几个数的乘积的形式,且其中一个因数是这个数.
11.因式分解与整式乘法互为逆变形,请利用a2+ab=a(a+b)解决下列问题:
(1)简便运算:8.72+8.7×1.3;
(2)判断n2+n(n为整数)是奇数还是偶数.
12.发现 任意五个连续整数的平方和是5的倍数.
验证
(1)(-1)2+02+12+22+32的结果是5的几倍?
(2)设五个连续整数的中间数为n,写出它们的平方和,并说明这五个连续整数的平方和是5的倍数.
延伸
任意三个连续整数的平方和被3除的余数是几呢?请说出理由.
教师详解详析
1.C
2.D [解析]
因为(x-3)(x+1)=x2-2x-3,
所以m=-2,n=-3.
3.解:(1)因为3(x2-6x+1)=3x2-18x+3≠3x2-9x+3,
所以小明分解得不对.
(2)因为(3x+2)(3x-2)=(3x)2-4=9x2-4,
所以小明分解得对.
4.B [解析]
逆用乘法对加法的分配律可得原式=99×(57+44-1)=99×100=9900.
5.a2+2ab=a(a+2b)(答案不唯一)
[解析]
把图形分割成一个正方形和两个长方形计算面积,则有a2+2ab=a(a+2b);
把图形分割成两个长方形,一边长分别是a+b,b,另一边长都是a,则有a(a+b)+ab=a(a+2b);
用整个图形的面积减去一个相邻两边长分别为a,a+b的长方形的面积,得到另外一个长方形的面积,这个长方形相邻两边长分别是a,b,即a(a+2b)-a(a+b)=ab.
6.⑤
7.ab+(a2+b2)=(a+b)2
8.解:原式=510+511=510+5×510=6×510=6×5×59=30×59.
因为30×59能被30整除,
所以255+511能被30整除.
9.解:因为x2-mx+4=(x-2)(x+n)=x2+(n-2)x-2n,
所以-m=n-2,-2n=4,
解得m=4,n=-2,
则mn=-8.
教师详解详析
1.D 2.② ①
3.B [解析]
(x+1)(x-3)=x2-2x-3,因此a=-2,b=-3.故选B.
4.解:∵(x+2)(x+6)=x2+8x+12,
∴m=8.
∵(x-1)(x-16)=x2-17x+16,
∴n=16.
5.解:(1)1
(2)设x3+2x+3=(x+1)(x2+ax+3),则x3+2x+3=x3+(a+1)x2+(a+3)x+3,
所以a+1=0,a+3=2,解得a=-1,故该多项式的另一个因式是x2-x+3.
6.C
7.解:(1)m-n (m-n)2
(2)(m+n)2-4mn=(m-n)2
(3)2m2+3mn+n2=(2m+n)(m+n).
8.解:(1)①正方形的面积=a2+2a+1;正方形的面积=(a+1)2.
②a2+2a+1=(a+1)2
(2)①答案不唯一.如图(a)所示,可推导出(a+b)2=a2+2ab+b2.
②如图(b)所示,2a2+5ab+2b2=(2a+b)(a+2b)(拼图不唯一).
9.解:原式=2.718×(23+59+18)=271.8.
10.解:1010-109×8+108×5=108×(102-10×8+5)=25×108,所以原式能被25整除.
11.解:(1)8.72+8.7×1.3=8.7×(8.7+1.3)=8.7×10=87.
(2)n2+n=n(n+1).
若n为奇数,则n+1为偶数;
若n为偶数,则n+1为奇数,
即n与n+1始终一奇一偶,所以n2+n是偶数.
12.解:验证
(1)(-1)2+02+12+22+32=1+0+1+4+9=15,15÷5=3,
即(-1)2+02+12+22+32的结果是5的3倍.
(2)若五个连续整数的中间数为n,则其余的整数是n-2,n-1,n+1,n+2,
它们的平方和为(n-2)2+(n-1)2+n2+(n+1)2+(n+2)2=n2-4n+4+n2-2n+1+n2+n2+2n+1+n2+4n+4=5n2+10.
∵5n2+10=5(n2+2),n是整数,
∴n2+2是整数,
∴这五个连续整数的平方和是5的倍数.
延伸 任意三个连续整数的平方和被3除的余数是2.理由:设三个连续整数的中间数为n,则其余的整数是n-1,n+1,
它们的平方和为(n-1)2+n2+(n+1)2=n2-2n+1+n2+n2+2n+1=3n2+2.
∵n是整数,∴n2是整数.
∵3n2能被3整除,∴3n2+2被3除的余数是2,
即任意三个连续整数的平方和被3除的余数是2.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
