2020-2021学年八年级数学北师大版下册课课练6.2.2利用对角线判定平行四边形(Word版,附答案)
文档属性
| 名称 | 2020-2021学年八年级数学北师大版下册课课练6.2.2利用对角线判定平行四边形(Word版,附答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 315.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-03 00:00:00 | ||
图片预览





文档简介
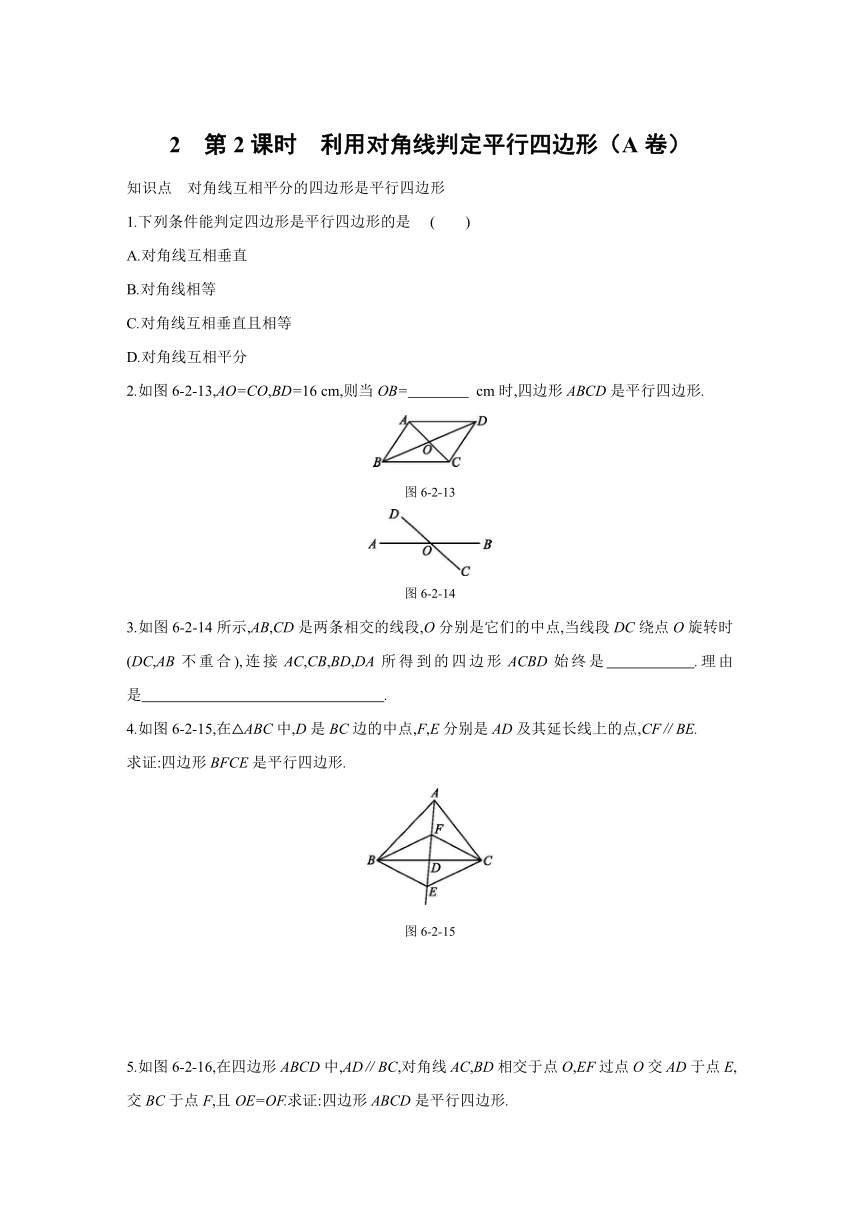
2 第2课时 利用对角线判定平行四边形(A卷)
知识点 对角线互相平分的四边形是平行四边形
1.下列条件能判定四边形是平行四边形的是
( )
A.对角线互相垂直
B.对角线相等
C.对角线互相垂直且相等
D.对角线互相平分
2.如图6-2-13,AO=CO,BD=16
cm,则当OB=
cm时,四边形ABCD是平行四边形.?
图6-2-13
图6-2-14
3.如图6-2-14所示,AB,CD是两条相交的线段,O分别是它们的中点,当线段DC绕点O旋转时(DC,AB不重合),连接AC,CB,BD,DA所得到的四边形ACBD始终是 .理由是 .?
4.如图6-2-15,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE.
求证:四边形BFCE是平行四边形.
图6-2-15
5.如图6-2-16,在四边形ABCD中,AD∥BC,对角线AC,BD相交于点O,EF过点O交AD于点E,交BC于点F,且OE=OF.求证:四边形ABCD是平行四边形.
图6-2-16
6.下列说法错误的是
( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
7.已知△ABC(如图6-2-17①),按图②、图③所示的尺规作图痕迹,不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是
( )
图6-2-17
A.两组对边分别平行的四边形是平行四边形
B.对角线互相平分的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.两组对边分别相等的四边形是平行四边形
图6-2-18
8.如图6-2-18,四边形ABCD的对角线相交于点O,从下列条件:①AD∥BC,②AB=CD,③AO=CO,④∠ABC=∠ADC中选出两个使四边形ABCD是平行四边形,则你选择的两个条件是 .(填序号)?
9.如图6-2-19,在△ABC中,D是BC上的点,O是AD的中点,过点A作BC的平行线交BO的延长线于点E,则四边形ABDE是平行四边形吗?说明理由.
图6-2-19
10.如图6-2-20,在?ABCD中,AC,BD相交于点O,E,F分别为OB,OD的中点,连接AF,CE,AE,CF.
(1)求证:四边形AECF是平行四边形;
(2)如果点E,F分别在DB和BD的延长线上,且满足BE=DF,那么(1)中的结论还成立吗?请说明理由.
图6-2-20
11.如图6-2-21①,在?ABCD中,O是对角线AC的中点,EF过点O,分别与AD,BC交于点E,F,GH过点O,分别与AB,CD交于点G,H,连接EG,FG,FH,EH.
(1)求证:四边形EGFH是平行四边形;
(2)如图②,若EF∥AB,GH∥BC,在不添加任何辅助线的情况下,请直接写出图②中所有与四边形AGHD面积相等的平行四边形.
图6-2-21
(B卷)
命题点
1 对角线互相平分的四边形是平行四边形
1.在下列给定的条件中,能作出平行四边形的是( )
A.以60为一条对角线长,20,34为两条邻边长
B.以20,36为对角线长,22为一条边长
C.以6为一条对角线长,3,10为两条邻边长
D.以6,10为对角线长,8为一条边长
2.2020·河南模拟
如图6-2-12,在四边形ABCD中,对角线AC,BD相交于点O,添加下列条件后仍不能判定四边形ABCD是平行四边形的是( )
A.AD∥BC,AO=CO
B.AD=BC,AO=OC
C.AD=BC,CD=AB
D.S△AOD=S△COD=S△BOC
3.2020·江苏建湖期中
如图6-2-13,BD是?ABCD的对角线,点E,F在BD上,要使四边形AECF是平行四边形,还需增加的一个条件是______________.
图6-2-13
4.已知四边形ABCD四个顶点的坐标分别是A(-,-),B(1,-1),C(,),D(-1,1),则四边形ABCD是不是平行四边形?若是,请给出证明.
5.如图6-2-14,在四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长,与AD的延长线相交于点F,连接CF,BD.四边形BDFC是平行四边形吗?证明你的结论.
图6-2-14
6.如图6-2-15所示,O是?ABCD的对角线AC的中点,过点O的直线EF与AB,CD分别交于E,F两点,连接AF,CE.
(1)求证:四边形AECF是平行四边形;
(2)填空:若不添加辅助线,则图中的全等三角形共有________对.
图6-2-15
7.2020·北京昌平区期中
如图6-2-16,在四边形ABCD中,AC,BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F,∠AEO=∠CFO,AD=BC.
(1)求证:O是线段AC的中点;
(2)连接AF,EC,求证:四边形AFCE是平行四边形.
图6-2-16
命题点
2 与平行四边形的判定有关的开放探究题
8.在如图6-2-17所示的网格中,以格点A,B,C,D,E,F中的4个点为顶点,你能画出的平行四边形有( )
图6-2-17
A.2个
B.3个
C.4个
D.5个
易错警示(8题)
按照平行四边形不同的判定方法逐个分析,以免遗漏.
9.如图6-2-18,在?ABCD中,O是对角线BD的中点,过点O的直线和AD,BC分别相交于点E,F,AM平分∠BAD交BD于点M,CN平分∠DCB交BD于点N.请在已知条件的基础上,构造新的平行四边形并加以证明.
图6-2-18
10.如图6-2-19,在△ABC中,D,E分别是AB,AC的中点,F是DE延长线上的点,且EF=DE.
(1)图中的平行四边形有哪几个?请说明理由;
(2)若△AEF的面积是3,求四边形BCFD的面积.
图6-2-19
11.2020·滕州期末
如图6-2-20,在?ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3
cm,BC=5
cm,点P从点A出发沿边AD向点D匀速运动,速度为1
cm/s,连接PO并延长交BC于点Q.设运动时间为t
s(0<t<5).
(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为y
cm2,当t=4时,求y的值.
图6-2-20
解题突破(11题)
(2)平行四边形被两条对角线分成的四个小三角形有什么关系?你能求出点O到BC边的距离吗?它与△OQC的面积有什么关系?
教师详解详析
1.D
2.8 [解析]
∵BD=16
cm,OB=8
cm,∴BO=DO.
又∵AO=CO,∴四边形ABCD是平行四边形.
3.平行四边形 对角线互相平分的四边形是平行四边形
4.证明:∵在△ABC中,D是BC边的中点,
∴BD=CD.
∵CF∥BE,∴∠CFD=∠BED.
在△CFD和△BED中,
∵∠CFD=∠BED,∠FDC=∠EDB,CD=BD,
∴△CFD≌△BED,∴DF=DE.
又∵BD=CD,
∴四边形BFCE是平行四边形.
5.证明:∵AD∥BC,∴∠AEO=∠CFO.
在△AEO和△CFO中,
∵∠AEO=∠CFO,OE=OF,∠EOA=∠FOC,
∴△AEO≌△CFO(ASA),∴AO=CO.
同理可证BO=DO,
∴四边形ABCD是平行四边形.
6.D 7.B
8.答案不唯一,如①③
9.解:四边形ABDE是平行四边形.
理由:∵AE∥BC,
∴∠OAE=∠ODB,∠AEO=∠DBO.
∵O是AD的中点,∴OA=OD,
∴△AOE≌△DOB,∴OE=OB.
又∵OA=OD,
∴四边形ABDE是平行四边形.
10.解:(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,F分别为OB,OD的中点,
∴OE=OB,OF=OD,∴OE=OF.
又∵OA=OC,
∴四边形AECF是平行四边形.
(2)(1)中的结论仍然成立.
理由:∵BE=DF,OB=OD,∴OE=OF.
又∵OA=OC,
∴四边形AECF是平行四边形,
即(1)中的结论仍然成立.
11.解:(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,OA=OC,∴∠EAO=∠FCO.
又∵∠AOE=∠COF,
∴△OAE≌△OCF,∴OE=OF.
同理可证OG=OH.
∴四边形EGFH是平行四边形.
(2)?GBCH,?ABFE,?EFCD,?EGFH.
教师详解详析
1.B [解析]
要想构成平行四边形,两条邻边和一条对角线必须能构成三角形,或者两条对角线的一半和平行四边形的一边能构成三角形.
2.B
3.BE=DF(答案不唯一)
4.解:四边形ABCD是平行四边形.
证明:∵A(-,-),B(1,-1),C(,),D(-1,1),
∴点A与点C关于原点O对称,点B与点D关于原点O对称,
∴OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
5.解:四边形BDFC是平行四边形.
证明:∵∠A=∠ABC=90°,
∴∠A+∠ABC=180°,
∴BC∥AF,∴∠BCE=∠FDE.
∵E是边CD的中点,∴CE=DE.
在△BCE和△FDE中,
∵∠BCE=∠FDE,CE=DE,∠CEB=∠DEF,
∴△BCE≌△FDE(ASA),∴BE=FE.
∵CE=DE,BE=FE,
∴四边形BDFC是平行四边形.
6.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠EAO=∠FCO.
∵O是AC的中点,∴OA=OC.
又∵∠EOA=∠FOC,
∴△AOE≌△COF,∴OE=OF.
又∵OA=OC,∴四边形AECF是平行四边形.
(2)6
7.证明:(1)∵∠AEO=∠CFO,
∴AE∥CF,即AD∥BC.
又∵AD=BC,
∴四边形ABCD是平行四边形.
∵AC,BD相交于点O,
∴O是线段AC的中点.
(2)∵O是线段AC的中点,
∴OA=OC.
∵AD∥BC,
∴∠EAC=∠FCA.
在△OAE和△OCF中,
∵∠EAO=∠FCO,AO=CO,∠AOE=∠COF,
∴△OAE≌△OCF(ASA),
∴OE=OF.
又∵OA=OC,
∴四边形AFCE是平行四边形.
8.B
9.解:(答案不唯一)如图,连接ME,EN,FN,FM,则四边形ENFM是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴∠BAD=∠DCB,AB=CD,AB∥CD,AD∥BC,∴∠ABM=∠CDN,∠EDO=∠FBO.
∵AM平分∠BAD,CN平分∠DCB,
∴∠BAM=∠DCN.
在△ABM和△CDN中,
∵∠ABM=∠CDN,AB=CD,∠BAM=∠DCN,∴△ABM≌△CDN,∴BM=DN.
∵O是对角线BD的中点,∴BO=DO,
∴OM=ON.
在△EDO和△FBO中,
∵∠EDO=∠FBO,DO=BO,∠EOD=∠FOB,
∴△EDO≌△FBO,∴OE=OF,
∴四边形ENFM是平行四边形.
10.解:(1)图中的平行四边形有:?ADCF,?BDFC,共2个.
理由:∵E是AC的中点,∴AE=CE.
又∵EF=DE,∴四边形ADCF是平行四边形,
∴AD∥CF,AD=CF.
∵D是AB的中点,∴AD=BD,∴BD=CF.
又∵BD∥CF,∴四边形BDFC是平行四边形.
(2)由(1)知四边形ADCF和四边形BDFC都是平行四边形,∴S△CEF=S△CED=S△AEF=3,
∴S△CDF=S△CED+S△CEF=6,
∴?BCFD的面积是12.
11.解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AO=CO,∴∠PAO=∠QCO.
在△APO和△CQO中,
∵∠PAO=∠QCO,AO=CO,∠POA=∠QOC,
∴△APO≌△CQO(ASA),
∴AP=CQ.
当四边形ABQP是平行四边形时,AP=BQ,
∴BQ=CQ=BC=
cm,
则AP=
cm,∴t=2.5.
即当t=2.5时,四边形ABQP是平行四边形.
(2)如图,过点O作ON⊥BC于点N.
∵AB⊥AC,AB=3
cm,BC=5
cm,
∴在Rt△ABC中,由勾股定理,得AC=4
cm,
∴=AB·AC=×3×4=6(cm2).
∵四边形ABCD是平行四边形,
∴S△BOC=S△COD=S△AOB=S△ABC=3
cm2,
∴BC·ON=3,则ON=1.2
cm.
当t=4时,AP=4
cm,则CQ=4
cm,
∴S△OQC=CQ·ON=×4×1.2=2.4(cm2),
∴S四边形OQCD=S△OQC+S△COD=5.4
cm2,
∴y=5.4.
知识点 对角线互相平分的四边形是平行四边形
1.下列条件能判定四边形是平行四边形的是
( )
A.对角线互相垂直
B.对角线相等
C.对角线互相垂直且相等
D.对角线互相平分
2.如图6-2-13,AO=CO,BD=16
cm,则当OB=
cm时,四边形ABCD是平行四边形.?
图6-2-13
图6-2-14
3.如图6-2-14所示,AB,CD是两条相交的线段,O分别是它们的中点,当线段DC绕点O旋转时(DC,AB不重合),连接AC,CB,BD,DA所得到的四边形ACBD始终是 .理由是 .?
4.如图6-2-15,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE.
求证:四边形BFCE是平行四边形.
图6-2-15
5.如图6-2-16,在四边形ABCD中,AD∥BC,对角线AC,BD相交于点O,EF过点O交AD于点E,交BC于点F,且OE=OF.求证:四边形ABCD是平行四边形.
图6-2-16
6.下列说法错误的是
( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
7.已知△ABC(如图6-2-17①),按图②、图③所示的尺规作图痕迹,不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是
( )
图6-2-17
A.两组对边分别平行的四边形是平行四边形
B.对角线互相平分的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.两组对边分别相等的四边形是平行四边形
图6-2-18
8.如图6-2-18,四边形ABCD的对角线相交于点O,从下列条件:①AD∥BC,②AB=CD,③AO=CO,④∠ABC=∠ADC中选出两个使四边形ABCD是平行四边形,则你选择的两个条件是 .(填序号)?
9.如图6-2-19,在△ABC中,D是BC上的点,O是AD的中点,过点A作BC的平行线交BO的延长线于点E,则四边形ABDE是平行四边形吗?说明理由.
图6-2-19
10.如图6-2-20,在?ABCD中,AC,BD相交于点O,E,F分别为OB,OD的中点,连接AF,CE,AE,CF.
(1)求证:四边形AECF是平行四边形;
(2)如果点E,F分别在DB和BD的延长线上,且满足BE=DF,那么(1)中的结论还成立吗?请说明理由.
图6-2-20
11.如图6-2-21①,在?ABCD中,O是对角线AC的中点,EF过点O,分别与AD,BC交于点E,F,GH过点O,分别与AB,CD交于点G,H,连接EG,FG,FH,EH.
(1)求证:四边形EGFH是平行四边形;
(2)如图②,若EF∥AB,GH∥BC,在不添加任何辅助线的情况下,请直接写出图②中所有与四边形AGHD面积相等的平行四边形.
图6-2-21
(B卷)
命题点
1 对角线互相平分的四边形是平行四边形
1.在下列给定的条件中,能作出平行四边形的是( )
A.以60为一条对角线长,20,34为两条邻边长
B.以20,36为对角线长,22为一条边长
C.以6为一条对角线长,3,10为两条邻边长
D.以6,10为对角线长,8为一条边长
2.2020·河南模拟
如图6-2-12,在四边形ABCD中,对角线AC,BD相交于点O,添加下列条件后仍不能判定四边形ABCD是平行四边形的是( )
A.AD∥BC,AO=CO
B.AD=BC,AO=OC
C.AD=BC,CD=AB
D.S△AOD=S△COD=S△BOC
3.2020·江苏建湖期中
如图6-2-13,BD是?ABCD的对角线,点E,F在BD上,要使四边形AECF是平行四边形,还需增加的一个条件是______________.
图6-2-13
4.已知四边形ABCD四个顶点的坐标分别是A(-,-),B(1,-1),C(,),D(-1,1),则四边形ABCD是不是平行四边形?若是,请给出证明.
5.如图6-2-14,在四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长,与AD的延长线相交于点F,连接CF,BD.四边形BDFC是平行四边形吗?证明你的结论.
图6-2-14
6.如图6-2-15所示,O是?ABCD的对角线AC的中点,过点O的直线EF与AB,CD分别交于E,F两点,连接AF,CE.
(1)求证:四边形AECF是平行四边形;
(2)填空:若不添加辅助线,则图中的全等三角形共有________对.
图6-2-15
7.2020·北京昌平区期中
如图6-2-16,在四边形ABCD中,AC,BD相交于点O,延长AD至点E,连接EO并延长交CB的延长线于点F,∠AEO=∠CFO,AD=BC.
(1)求证:O是线段AC的中点;
(2)连接AF,EC,求证:四边形AFCE是平行四边形.
图6-2-16
命题点
2 与平行四边形的判定有关的开放探究题
8.在如图6-2-17所示的网格中,以格点A,B,C,D,E,F中的4个点为顶点,你能画出的平行四边形有( )
图6-2-17
A.2个
B.3个
C.4个
D.5个
易错警示(8题)
按照平行四边形不同的判定方法逐个分析,以免遗漏.
9.如图6-2-18,在?ABCD中,O是对角线BD的中点,过点O的直线和AD,BC分别相交于点E,F,AM平分∠BAD交BD于点M,CN平分∠DCB交BD于点N.请在已知条件的基础上,构造新的平行四边形并加以证明.
图6-2-18
10.如图6-2-19,在△ABC中,D,E分别是AB,AC的中点,F是DE延长线上的点,且EF=DE.
(1)图中的平行四边形有哪几个?请说明理由;
(2)若△AEF的面积是3,求四边形BCFD的面积.
图6-2-19
11.2020·滕州期末
如图6-2-20,在?ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3
cm,BC=5
cm,点P从点A出发沿边AD向点D匀速运动,速度为1
cm/s,连接PO并延长交BC于点Q.设运动时间为t
s(0<t<5).
(1)当t为何值时,四边形ABQP是平行四边形?
(2)设四边形OQCD的面积为y
cm2,当t=4时,求y的值.
图6-2-20
解题突破(11题)
(2)平行四边形被两条对角线分成的四个小三角形有什么关系?你能求出点O到BC边的距离吗?它与△OQC的面积有什么关系?
教师详解详析
1.D
2.8 [解析]
∵BD=16
cm,OB=8
cm,∴BO=DO.
又∵AO=CO,∴四边形ABCD是平行四边形.
3.平行四边形 对角线互相平分的四边形是平行四边形
4.证明:∵在△ABC中,D是BC边的中点,
∴BD=CD.
∵CF∥BE,∴∠CFD=∠BED.
在△CFD和△BED中,
∵∠CFD=∠BED,∠FDC=∠EDB,CD=BD,
∴△CFD≌△BED,∴DF=DE.
又∵BD=CD,
∴四边形BFCE是平行四边形.
5.证明:∵AD∥BC,∴∠AEO=∠CFO.
在△AEO和△CFO中,
∵∠AEO=∠CFO,OE=OF,∠EOA=∠FOC,
∴△AEO≌△CFO(ASA),∴AO=CO.
同理可证BO=DO,
∴四边形ABCD是平行四边形.
6.D 7.B
8.答案不唯一,如①③
9.解:四边形ABDE是平行四边形.
理由:∵AE∥BC,
∴∠OAE=∠ODB,∠AEO=∠DBO.
∵O是AD的中点,∴OA=OD,
∴△AOE≌△DOB,∴OE=OB.
又∵OA=OD,
∴四边形ABDE是平行四边形.
10.解:(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,F分别为OB,OD的中点,
∴OE=OB,OF=OD,∴OE=OF.
又∵OA=OC,
∴四边形AECF是平行四边形.
(2)(1)中的结论仍然成立.
理由:∵BE=DF,OB=OD,∴OE=OF.
又∵OA=OC,
∴四边形AECF是平行四边形,
即(1)中的结论仍然成立.
11.解:(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,OA=OC,∴∠EAO=∠FCO.
又∵∠AOE=∠COF,
∴△OAE≌△OCF,∴OE=OF.
同理可证OG=OH.
∴四边形EGFH是平行四边形.
(2)?GBCH,?ABFE,?EFCD,?EGFH.
教师详解详析
1.B [解析]
要想构成平行四边形,两条邻边和一条对角线必须能构成三角形,或者两条对角线的一半和平行四边形的一边能构成三角形.
2.B
3.BE=DF(答案不唯一)
4.解:四边形ABCD是平行四边形.
证明:∵A(-,-),B(1,-1),C(,),D(-1,1),
∴点A与点C关于原点O对称,点B与点D关于原点O对称,
∴OA=OC,OB=OD,
∴四边形ABCD是平行四边形.
5.解:四边形BDFC是平行四边形.
证明:∵∠A=∠ABC=90°,
∴∠A+∠ABC=180°,
∴BC∥AF,∴∠BCE=∠FDE.
∵E是边CD的中点,∴CE=DE.
在△BCE和△FDE中,
∵∠BCE=∠FDE,CE=DE,∠CEB=∠DEF,
∴△BCE≌△FDE(ASA),∴BE=FE.
∵CE=DE,BE=FE,
∴四边形BDFC是平行四边形.
6.解:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠EAO=∠FCO.
∵O是AC的中点,∴OA=OC.
又∵∠EOA=∠FOC,
∴△AOE≌△COF,∴OE=OF.
又∵OA=OC,∴四边形AECF是平行四边形.
(2)6
7.证明:(1)∵∠AEO=∠CFO,
∴AE∥CF,即AD∥BC.
又∵AD=BC,
∴四边形ABCD是平行四边形.
∵AC,BD相交于点O,
∴O是线段AC的中点.
(2)∵O是线段AC的中点,
∴OA=OC.
∵AD∥BC,
∴∠EAC=∠FCA.
在△OAE和△OCF中,
∵∠EAO=∠FCO,AO=CO,∠AOE=∠COF,
∴△OAE≌△OCF(ASA),
∴OE=OF.
又∵OA=OC,
∴四边形AFCE是平行四边形.
8.B
9.解:(答案不唯一)如图,连接ME,EN,FN,FM,则四边形ENFM是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴∠BAD=∠DCB,AB=CD,AB∥CD,AD∥BC,∴∠ABM=∠CDN,∠EDO=∠FBO.
∵AM平分∠BAD,CN平分∠DCB,
∴∠BAM=∠DCN.
在△ABM和△CDN中,
∵∠ABM=∠CDN,AB=CD,∠BAM=∠DCN,∴△ABM≌△CDN,∴BM=DN.
∵O是对角线BD的中点,∴BO=DO,
∴OM=ON.
在△EDO和△FBO中,
∵∠EDO=∠FBO,DO=BO,∠EOD=∠FOB,
∴△EDO≌△FBO,∴OE=OF,
∴四边形ENFM是平行四边形.
10.解:(1)图中的平行四边形有:?ADCF,?BDFC,共2个.
理由:∵E是AC的中点,∴AE=CE.
又∵EF=DE,∴四边形ADCF是平行四边形,
∴AD∥CF,AD=CF.
∵D是AB的中点,∴AD=BD,∴BD=CF.
又∵BD∥CF,∴四边形BDFC是平行四边形.
(2)由(1)知四边形ADCF和四边形BDFC都是平行四边形,∴S△CEF=S△CED=S△AEF=3,
∴S△CDF=S△CED+S△CEF=6,
∴?BCFD的面积是12.
11.解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AO=CO,∴∠PAO=∠QCO.
在△APO和△CQO中,
∵∠PAO=∠QCO,AO=CO,∠POA=∠QOC,
∴△APO≌△CQO(ASA),
∴AP=CQ.
当四边形ABQP是平行四边形时,AP=BQ,
∴BQ=CQ=BC=
cm,
则AP=
cm,∴t=2.5.
即当t=2.5时,四边形ABQP是平行四边形.
(2)如图,过点O作ON⊥BC于点N.
∵AB⊥AC,AB=3
cm,BC=5
cm,
∴在Rt△ABC中,由勾股定理,得AC=4
cm,
∴=AB·AC=×3×4=6(cm2).
∵四边形ABCD是平行四边形,
∴S△BOC=S△COD=S△AOB=S△ABC=3
cm2,
∴BC·ON=3,则ON=1.2
cm.
当t=4时,AP=4
cm,则CQ=4
cm,
∴S△OQC=CQ·ON=×4×1.2=2.4(cm2),
∴S四边形OQCD=S△OQC+S△COD=5.4
cm2,
∴y=5.4.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
