2020-2021学年八年级数学人教版下册课件-18.1.1 平行四边形的性质(24张)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册课件-18.1.1 平行四边形的性质(24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
课前三分钟:
两会热词解读——财税改革
2018年政府工作报告指出,坚持以推进供给侧结构性改革为主线。必须把改善供给侧结构作为主攻方向,通过简政减税、放宽准入、鼓励创新,持续激发微观主体活力,减少无效供给、扩大有效供给,更好适应和引导需求。
小区的伸缩门
图片欣赏
香港
观
察:
活动一:图片欣赏---生活中的四边形
活
动
三
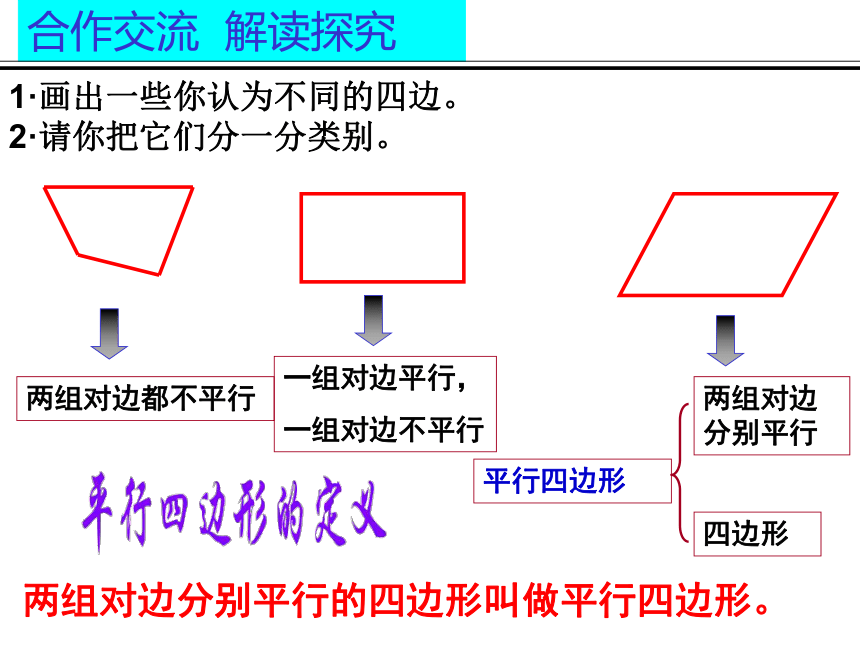
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
两组对边分别平行的四边形叫做平行四边形。
合作交流
解读探究
1·画出一些你认为不同的四边。
2·请你把它们分一分类别。
1、定义:
有两组对边分别平行的四边形叫做平行四边形。
A
B
D
C
解读探究
四边形ABCD是平行四边形
2、记作:
ABCD
4、两要素:
四边形
两组对边分别平行
5、几何语言:
AB∥CD
AD∥BC
3、读作:平行四边形ABCD
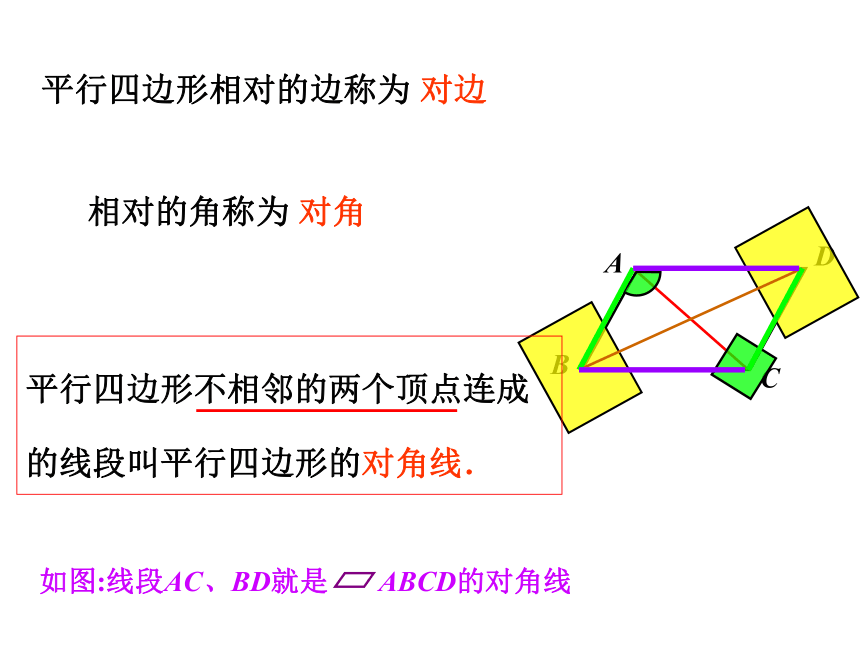
如图:线段AC、BD就是
ABCD的对角线
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
平行四边形相对的边称为
对边
相对的角称为
对角
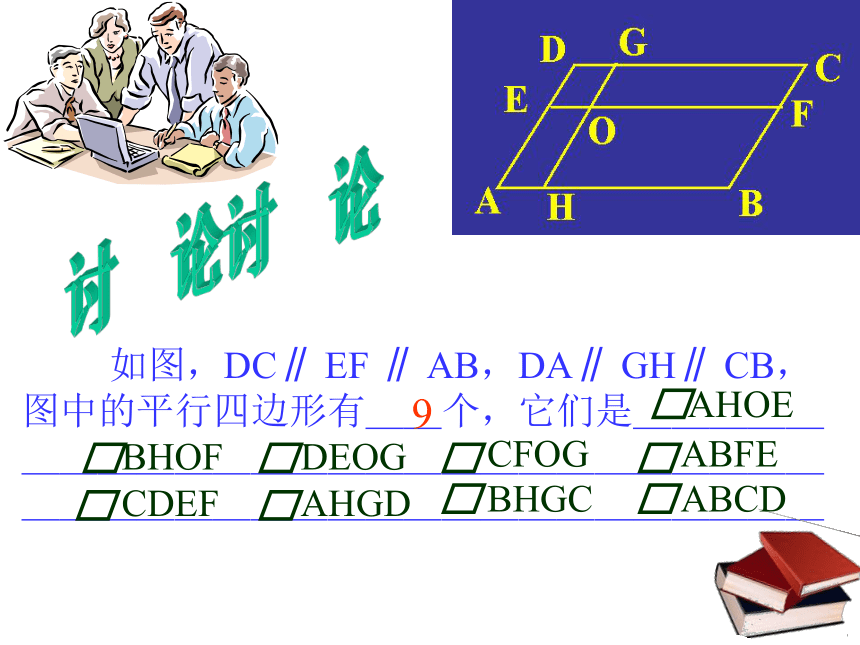
如图,DC∥
EF
∥
AB,DA∥
GH∥
CB,图中的平行四边形有__个,它们是_______________________________________________
讨
论
9
AHOE
ABCD
BHGC
AHGD
CDEF
ABFE
CFOG
DEOG
BHOF
拼
一
拼
取两个全等的三角形纸片,将它们的相等的一边重合,得到一个四边形。
你拼出了怎样的四边形?
拼
一
拼
两个全等三角形可以拼出一个平行四边形,反之一个平行四边形可以分割两个全等三角形。
根据定义画一个平行四边形,观察这个四边形,除了
“两组对边分别平行”以外,它的边、角之间有什么关系吗?度量一下,是不是和你的猜想一致?还有别的方法吗?
心动不如行动,跃跃欲试不如亲自尝试
活
动
二
学习目标
预习检测
例题赏析
达标测试
拓展测试
谈谈收获
活
动
一
A
B
C
D
猜想二
平行四边形的对角有什么关系?邻角呢?怎么得到这个关系?
方法一
观察、度量
D
方法二
剪开、叠合
C
A
B
方法三
证明
该怎样证明呢?
平行四边形的对边相等,对角相等。
验证
已知:四边形ABCD是平行四边形。
求证:AB=CD,AD=BC
∠A=
∠C,
∠B=
∠D.
C
B
D
A
提示:可连接AC,试证⊿______≌
⊿______
转化思想:
四边形
问题
三角形
问题
转化
已知:
四边形
ABCD是平行四边形(如图)
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
即∠BAD=∠DCB
证明:连结AC
∵AB∥CD,AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
又∵AC=AC
∴
ABC≌
CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
A
B
C
D
1
2
3
4
∵四边形
ABCD是平行四边形(已知)
平行四边形的性质
元素
性质
符号语言
图形
边
角
平行四边形
平行四边形
平行四边形
四边形ABCD是平行四边形
∥
∥
A
B
C
D
四边形ABCD是平行四边
=
=
四边形ABCD是平行四边形
的对边平行
AB
CD
AD
BC
AB
CD
AD
BC
∠A=
∠B
=
∠D
∠C
的对边相等
的对角相等
www..cn
1、如图:在
ABCD中,根据已知
你能得到哪些结论?为什么?
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
小试牛刀:
小结:平行四边形中知道其中一角可求出另外三个角的度数。
1、如图,
ABCD中,∠B=50°
则∠A= ;∠C= ;
∠D= .
B
C
D
A
2、□
ABCD中,
AB=3cm,
BC=5cm,
则AD=
,CD=
.
B
C
A
D
3、在□ABCD中,∠A+∠C=120°,
∠B= ;∠D=
;
A
B
C
D
50°
130°
130°
3cm
5cm
120°
120°
证明:
∵四边形ABCD是平行四边形
(已知)
例1
如图,在
ABCD中,DE⊥AB,BF⊥CD,垂足分别为E、F.
求证:AE=CF
例
题
教
学
A
B
C
D
E
F
∴∠A=∠C,
AD=CB.
(平行四边形的对角相等、
对边相等)
∴
∠AED=∠CFB=90°,
(垂直的定义)
∴△DAE≌△BCF(AAS)
∴AE=CF.
(全等三角形的对应边相等)
又∵
DE⊥AB,BF⊥CD(已知)
学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
A
B
C
平行四边形的对边平行且相等;
B
D
C
A
平行四边形的对角相等;邻角互补。
有两组对边分别平行的四边形是平行四边形。
完成课本习题19.1
第1、2、6题.
预习课本P85~86的内容
.
活动
一
活动
二
活动
三
活动
四
活动
五
作业
再见!
祝同学们学习进步!
课前三分钟:
两会热词解读——财税改革
2018年政府工作报告指出,坚持以推进供给侧结构性改革为主线。必须把改善供给侧结构作为主攻方向,通过简政减税、放宽准入、鼓励创新,持续激发微观主体活力,减少无效供给、扩大有效供给,更好适应和引导需求。
小区的伸缩门
图片欣赏
香港
观
察:
活动一:图片欣赏---生活中的四边形
活
动
三
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
四边形
平行四边形
两组对边分别平行的四边形叫做平行四边形。
合作交流
解读探究
1·画出一些你认为不同的四边。
2·请你把它们分一分类别。
1、定义:
有两组对边分别平行的四边形叫做平行四边形。
A
B
D
C
解读探究
四边形ABCD是平行四边形
2、记作:
ABCD
4、两要素:
四边形
两组对边分别平行
5、几何语言:
AB∥CD
AD∥BC
3、读作:平行四边形ABCD
如图:线段AC、BD就是
ABCD的对角线
A
D
C
B
平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
平行四边形相对的边称为
对边
相对的角称为
对角
如图,DC∥
EF
∥
AB,DA∥
GH∥
CB,图中的平行四边形有__个,它们是_______________________________________________
讨
论
9
AHOE
ABCD
BHGC
AHGD
CDEF
ABFE
CFOG
DEOG
BHOF
拼
一
拼
取两个全等的三角形纸片,将它们的相等的一边重合,得到一个四边形。
你拼出了怎样的四边形?
拼
一
拼
两个全等三角形可以拼出一个平行四边形,反之一个平行四边形可以分割两个全等三角形。
根据定义画一个平行四边形,观察这个四边形,除了
“两组对边分别平行”以外,它的边、角之间有什么关系吗?度量一下,是不是和你的猜想一致?还有别的方法吗?
心动不如行动,跃跃欲试不如亲自尝试
活
动
二
学习目标
预习检测
例题赏析
达标测试
拓展测试
谈谈收获
活
动
一
A
B
C
D
猜想二
平行四边形的对角有什么关系?邻角呢?怎么得到这个关系?
方法一
观察、度量
D
方法二
剪开、叠合
C
A
B
方法三
证明
该怎样证明呢?
平行四边形的对边相等,对角相等。
验证
已知:四边形ABCD是平行四边形。
求证:AB=CD,AD=BC
∠A=
∠C,
∠B=
∠D.
C
B
D
A
提示:可连接AC,试证⊿______≌
⊿______
转化思想:
四边形
问题
三角形
问题
转化
已知:
四边形
ABCD是平行四边形(如图)
求证:AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB
即∠BAD=∠DCB
证明:连结AC
∵AB∥CD,AD∥BC(平行四边形的对边平行)
∴∠1=∠2,∠3=∠4
又∵AC=AC
∴
ABC≌
CDA(ASA)
∴AB=CD,BC=DA,∠B=∠D
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
A
B
C
D
1
2
3
4
∵四边形
ABCD是平行四边形(已知)
平行四边形的性质
元素
性质
符号语言
图形
边
角
平行四边形
平行四边形
平行四边形
四边形ABCD是平行四边形
∥
∥
A
B
C
D
四边形ABCD是平行四边
=
=
四边形ABCD是平行四边形
的对边平行
AB
CD
AD
BC
AB
CD
AD
BC
∠A=
∠B
=
∠D
∠C
的对边相等
的对角相等
www..cn
1、如图:在
ABCD中,根据已知
你能得到哪些结论?为什么?
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
小试牛刀:
小结:平行四边形中知道其中一角可求出另外三个角的度数。
1、如图,
ABCD中,∠B=50°
则∠A= ;∠C= ;
∠D= .
B
C
D
A
2、□
ABCD中,
AB=3cm,
BC=5cm,
则AD=
,CD=
.
B
C
A
D
3、在□ABCD中,∠A+∠C=120°,
∠B= ;∠D=
;
A
B
C
D
50°
130°
130°
3cm
5cm
120°
120°
证明:
∵四边形ABCD是平行四边形
(已知)
例1
如图,在
ABCD中,DE⊥AB,BF⊥CD,垂足分别为E、F.
求证:AE=CF
例
题
教
学
A
B
C
D
E
F
∴∠A=∠C,
AD=CB.
(平行四边形的对角相等、
对边相等)
∴
∠AED=∠CFB=90°,
(垂直的定义)
∴△DAE≌△BCF(AAS)
∴AE=CF.
(全等三角形的对应边相等)
又∵
DE⊥AB,BF⊥CD(已知)
学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?
A1
A3
A2
A
B
C
平行四边形的对边平行且相等;
B
D
C
A
平行四边形的对角相等;邻角互补。
有两组对边分别平行的四边形是平行四边形。
完成课本习题19.1
第1、2、6题.
预习课本P85~86的内容
.
活动
一
活动
二
活动
三
活动
四
活动
五
作业
再见!
祝同学们学习进步!
