2020-2021学年九年级数学北师大版上册 第三章 概率的进一步研究 习题练习一(word版含解析)
文档属性
| 名称 | 2020-2021学年九年级数学北师大版上册 第三章 概率的进一步研究 习题练习一(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 170.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 13:09:59 | ||
图片预览



文档简介
北师大版九年级上册数学
第三章
概率的进一步研究
习题练习三(附答案)
一、选择题
1.从生产的一批螺钉中抽取1000个进行质量检查,结果发现有5个是次品,那么从中任取1个是次品概率约为(
).
A.
B.
C.
D.
2.某人做投硬币试验时,投掷次,正面朝上次(即正面朝上的频率),则下列说法正确的是( )
A.一定等于
B.一定不等于
C.
多投一次,更接近
D.
投掷次数逐渐增加,稳定在附近
3.在一个不透明的口袋中,装有3个红球,2个白球,除颜色不同外,其余都相同,则随机从口袋中摸出一个球为红色的概率是(
)
A.
B.
C.
D.
4.有一个不透明的盒子中装有个除颜色外完全相同的球,这个球中只有3个红球,若每次将球充分搅匀后,任意摸出一个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则的值大约是(
)
A.
12
B.
15
C.
18
D.
21
5.红红和娜娜按下图所示的规则玩“锤子、剪刀、布”游戏,
游戏规则:若一人出“剪刀”,另一人出“布”,则出“剪刀”者胜;若一人出“锤子”,另一人出“剪刀”,则出“锤子”者胜;若一人出“布”,另一人出“锤子”,则出“布”者胜,若两人出相同的手势,则两人平局.下列说法中错误的是
A.
红红不是胜就是输,所以红红胜的概率为
B.
红红胜或娜娜胜的概率相等
C.
两人出相同手势的概率为
D.
娜娜胜的概率和两人出相同手势的概率一样
6.用频率估计概率,可以发现,抛掷硬币,“正面朝上”的概率为0.5,是指(
)
A.
连续掷2次,结果一定是“正面朝上”和“反面朝上”各1次
B.
连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次
C.
抛掷2n次硬币,恰好有n次“正面朝上”
D.
抛掷n次,当n越来越大时,正面朝上的频率会越来越稳定于0.5
7.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为(
)
A.
20
B.
24
C.
28
D.
30
二、填空题
8.在一个不透明的布袋中装有50个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到白球的频率稳定在0.3左右,则布袋中白球可能有___________个;
9.如图,飞镖游戏板中每一块小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是_________.
10.小明有两双不同的运动鞋,上学时,小明从中任意拿出两只,恰好能配成一双的概率是_____.
11.有50个数据,把它们分成五组,第一、二、三、四、五组的数据个数分别是3,7,14、x、6,则第四组的频率为_____.
12.一个不透明的袋中装有除颜色外均相同的9个红球,3个白球,若干个绿球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,经过大量重复实验后,发现摸到绿球的概率稳定在0.2,则袋中有绿球______个.
13.有两双完全相同的鞋,从中任取两只,恰好成为一双的概率为_____.
14.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球标号的和等于5的概率是_____.
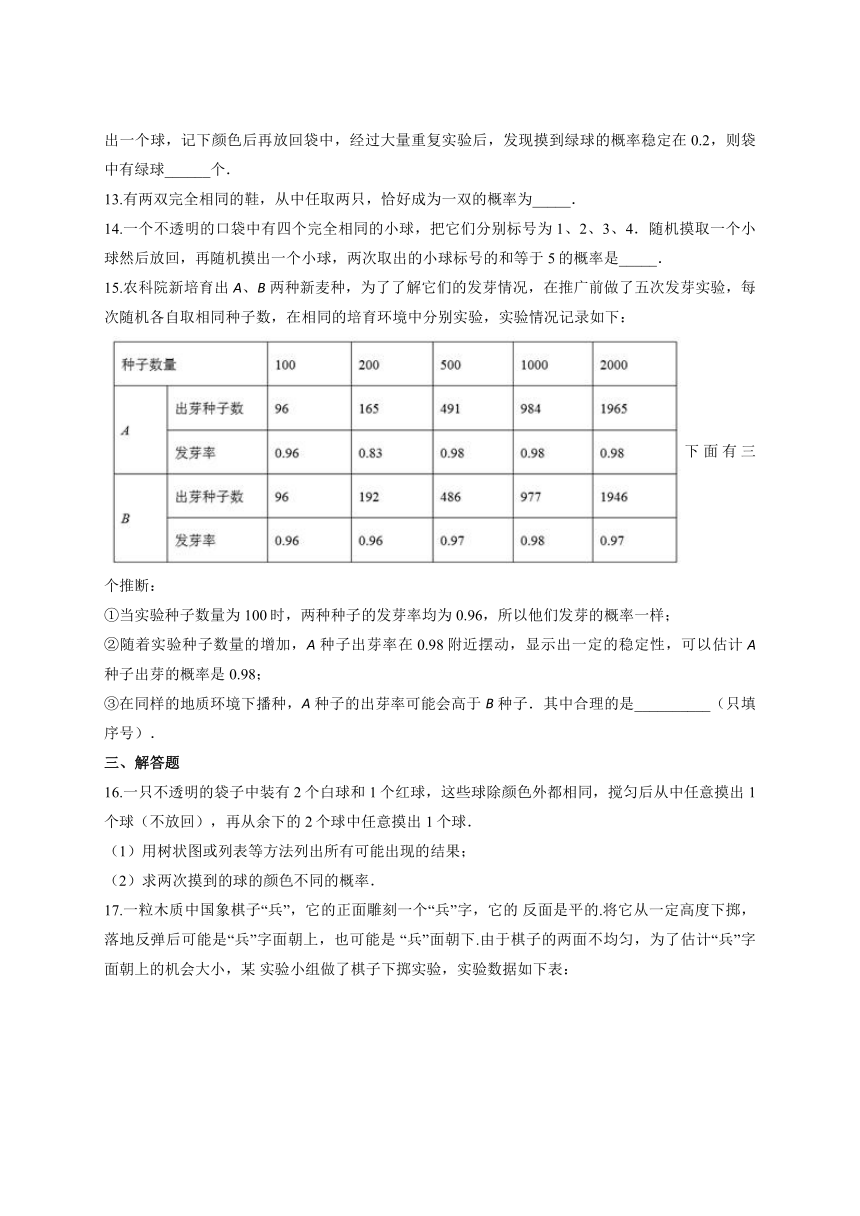
15.农科院新培育出A、B两种新麦种,为了了解它们的发芽情况,在推广前做了五次发芽实验,每次随机各自取相同种子数,在相同的培育环境中分别实验,实验情况记录如下:
下面有三个推断:
①当实验种子数量为100时,两种种子的发芽率均为0.96,所以他们发芽的概率一样;
②随着实验种子数量的增加,A种子出芽率在0.98附近摆动,显示出一定的稳定性,可以估计A种子出芽的概率是0.98;
③在同样的地质环境下播种,A种子的出芽率可能会高于B种子.其中合理的是__________(只填序号).
三、解答题
16.一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.
(1)用树状图或列表等方法列出所有可能出现的结果;
(2)求两次摸到的球的颜色不同的概率.
17.一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的
反面是平的.将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是
“兵”面朝下.由于棋子的两面不均匀,为了估计“兵”字面朝上的机会大小,某
实验小组做了棋子下掷实验,实验数据如下表:
(1)请将数据表补充完整:
(2)在图中画出“兵”字面朝上的频率分布折线图:
(3)如果实验继续进行下去,根据上表的数据,这个实验所得频率将逐渐稳定到某
一个数值附近,请你估计该随机事件在每次实验时发生的机会大小.
答案解析
1.【答案】B
【解析】直接根据求概率的公式即可得到结果.
因为抽取1000个进行质量检验,结果发现有10个次品,所以从中抽取一个是次品的概率约为,
故选B.
2.【答案】D
【解析】∵硬币只有正反两面,
∴投掷时正面朝上的概率为,
根据频率的概念可知投掷次数逐渐增加,P稳定在附近,
故选D.
3.【答案】A.
【解析】根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.因此,
∵袋子中球的总数为2+3=5,红球有3个,∴摸出红球的概率为.故选A.
4.【答案】B
【解析】在同样的条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,列出方程求解.解
解:由题意得,×100%=20%,
解得,a=15.
故选B.
5.【答案】A
【解析】红红和娜娜玩“锤子、剪刀、布”游戏,所有可能出现的结果列表如下:
由表格可知,共有9种等可能情况.其中平局的有3种:(锤子,锤子)、(剪刀,剪刀)、(布,布).因此,红红和娜娜两人出相同手势的概率为,两人获胜的概率都为,红红不是胜就是输,所以红红胜的概率为,错误,故选项A符合题意,故选项B,C,D不合题意;故选A.
6.【答案】D
【解析】利用“大量重复试验中,事件发生的频率逐渐稳定到某个常数附近,这个常数可以估计事件发生的概率”.连续抛掷2n次不一定正好正面向上和反面向上的次数各一半,故A、B、C错误,
抛掷n次,当n越来越大时,正面朝上的频率会越来越稳定于0.5,故D正确.
故选D.
7.【答案】D
【解析】根据题意得=30%,解得n=30,所以这个不透明的盒子里大约有30个除颜色外其他完全相同的小球.
故选D.
8.【答案】15.
【解析】利用频率估计概率得到摸到白球的概率为0.3,然后根据概率公式计算即可.
解:设袋子中白球有x个,根据题意,得:=0.30,解得:x=15,即布袋中白球可能有15个,故答案为:15.
9.【答案】
【解析】根据几何概率的求法:飞镖落在阴影部分的概率就是阴影区域的面积与总面积的比值.
∵总面积为3×3=9,其中阴影部分面积为4××1×2=4,
∴飞镖落在阴影部分的概率是,
故答案为:.
10.【答案】.
【解析】设其中一双鞋分别为a,a′;另一双鞋分别为b,b′,然后根据题意画树状图,由树状图即可求得所有等可能的结果与恰好能配成一双的情况,再利用概率公式即可求得答案.
设其中一双鞋分别为a,a′;另一双鞋分别为b,b′.
画树状图得:
∵共有12种等可能的结果,恰好能配成一双的有4种情况,
∴恰好能配成一双的概率是:=,
故答案为:.
11.【答案】0.4
【解析】根据各小组频数之和等于数据总和,即可求出第四组的频数,再根据频率=频数÷总数,进行计算.
解:根据题意,得:x=50-3-7-14-6=20,
∴第四组的频率为:.
故答案为:0.4.
12.【答案】3.
【解析】设绿球的个数为x,根据题意,得:=0.2,解得:x=3,经检验x=3是原分式方程的解,即袋中有绿球3个,故答案为:3.
13.【答案】
【解析】设其中一双鞋分别为a,a′;画出树状图,可知共有12种情况,能配成一双的有8种情况,根据概率公式计算即可;
设其中一双鞋分别为a,a′.画树状图得:
∵共有12种情况,能配成一双的有8种情况,∴取出两只刚好配一双鞋的概率是:.
故答案为:.
14.【答案】
【解析】先利用树状图列出两次取出的小球标号和的所有可能情况数,再找出两次取出的小球标号的和等于5的情况数,最后求出概率即可.
两次取出的小球标号和的所有可能情况共有16种,其中和为5的情况有4种,故两次取出的小球标号的和等于5的概率是4÷16=.故答案为.
15.【答案】②③
【解析】根据随机事件发生的“频率”与“概率”的关系进行分析解答即可.
(1)由表中的数据可知,当实验种子数量为100时,两种种子的发芽率虽然都是96%,但结合后续实验数据可知,此时的发芽率并不稳定,故不能确定两种种子发芽的概率就是96%,所以①中的说法不合理;
(2)由表中数据可知,随着实验次数的增加,A种种子发芽的频率逐渐稳定在98%左右,故可以估计A种种子发芽的概率是98%,所以②中的说法是合理的;
(3)由表中数据可知,随着实验次数的增加,A种种子发芽的频率逐渐稳定在98%左右,而B种种子发芽的频率稳定在97%左右,故可以估计在相同条件下,A种种子发芽率大于B种种子发芽率,所以③中的说法是合理的.
故答案为:②③.
16.【答案】(1)详见解析;(2).
【解析】(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由(1)中树状图可求得两次摸到的球的颜色不同的情况有4种,再利用概率公式求解即可求得答案.
(1)如图:
,
所有可能的结果为(白1,白2)、(白1,红)、(白2,白1)、(白2,红)、(红,白1)、(红,白2);
(2)共有6种情况,两次摸到的球的颜色不同的情况有4种,概率为.
17.【答案】(1)18,0.55;(2)见详解;(3)0.55
【解析】(1)根据图中信息,用频数除以实验次数,得到频率,由于试验次数较多,可以用频率估计概率;
(2)将频率作为纵坐标,试验次数作为横坐标,描点连线,可得折线图.
(3)根据表中数据,试验频率为0.7,0.45,0.63,0.59,0.52,0.55,0.56,0.55稳定在0.55左右,即可估计概率的大小.
解:(1)所填数字为:40×0.45=18,66÷120=0.55;
故答案为:18,0.55;
(2)折线图如下:
(3)根据表中数据,试验频率为0.7,0.45,0.63,0.59,0.52,0.55,0.56,0.55稳定在0.55左右,
故估计概率的大小为:0.55.
第三章
概率的进一步研究
习题练习三(附答案)
一、选择题
1.从生产的一批螺钉中抽取1000个进行质量检查,结果发现有5个是次品,那么从中任取1个是次品概率约为(
).
A.
B.
C.
D.
2.某人做投硬币试验时,投掷次,正面朝上次(即正面朝上的频率),则下列说法正确的是( )
A.一定等于
B.一定不等于
C.
多投一次,更接近
D.
投掷次数逐渐增加,稳定在附近
3.在一个不透明的口袋中,装有3个红球,2个白球,除颜色不同外,其余都相同,则随机从口袋中摸出一个球为红色的概率是(
)
A.
B.
C.
D.
4.有一个不透明的盒子中装有个除颜色外完全相同的球,这个球中只有3个红球,若每次将球充分搅匀后,任意摸出一个球记下颜色再放回盒子.通过大量重复试验后,发现摸到红球的频率稳定在20%左右,则的值大约是(
)
A.
12
B.
15
C.
18
D.
21
5.红红和娜娜按下图所示的规则玩“锤子、剪刀、布”游戏,
游戏规则:若一人出“剪刀”,另一人出“布”,则出“剪刀”者胜;若一人出“锤子”,另一人出“剪刀”,则出“锤子”者胜;若一人出“布”,另一人出“锤子”,则出“布”者胜,若两人出相同的手势,则两人平局.下列说法中错误的是
A.
红红不是胜就是输,所以红红胜的概率为
B.
红红胜或娜娜胜的概率相等
C.
两人出相同手势的概率为
D.
娜娜胜的概率和两人出相同手势的概率一样
6.用频率估计概率,可以发现,抛掷硬币,“正面朝上”的概率为0.5,是指(
)
A.
连续掷2次,结果一定是“正面朝上”和“反面朝上”各1次
B.
连续抛掷100次,结果一定是“正面朝上”和“反面朝上”各50次
C.
抛掷2n次硬币,恰好有n次“正面朝上”
D.
抛掷n次,当n越来越大时,正面朝上的频率会越来越稳定于0.5
7.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球,每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球实验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为(
)
A.
20
B.
24
C.
28
D.
30
二、填空题
8.在一个不透明的布袋中装有50个黄、白两种颜色的球,除颜色外其他都相同,小红通过多次摸球试验后发现,摸到白球的频率稳定在0.3左右,则布袋中白球可能有___________个;
9.如图,飞镖游戏板中每一块小正方形除颜色外都相同.若某人向游戏板投掷飞镖一次(假设飞镖落在游戏板上),则飞镖落在阴影部分的概率是_________.
10.小明有两双不同的运动鞋,上学时,小明从中任意拿出两只,恰好能配成一双的概率是_____.
11.有50个数据,把它们分成五组,第一、二、三、四、五组的数据个数分别是3,7,14、x、6,则第四组的频率为_____.
12.一个不透明的袋中装有除颜色外均相同的9个红球,3个白球,若干个绿球,每次摇匀后随机摸出一个球,记下颜色后再放回袋中,经过大量重复实验后,发现摸到绿球的概率稳定在0.2,则袋中有绿球______个.
13.有两双完全相同的鞋,从中任取两只,恰好成为一双的概率为_____.
14.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1、2、3、4.随机摸取一个小球然后放回,再随机摸出一个小球,两次取出的小球标号的和等于5的概率是_____.
15.农科院新培育出A、B两种新麦种,为了了解它们的发芽情况,在推广前做了五次发芽实验,每次随机各自取相同种子数,在相同的培育环境中分别实验,实验情况记录如下:
下面有三个推断:
①当实验种子数量为100时,两种种子的发芽率均为0.96,所以他们发芽的概率一样;
②随着实验种子数量的增加,A种子出芽率在0.98附近摆动,显示出一定的稳定性,可以估计A种子出芽的概率是0.98;
③在同样的地质环境下播种,A种子的出芽率可能会高于B种子.其中合理的是__________(只填序号).
三、解答题
16.一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球(不放回),再从余下的2个球中任意摸出1个球.
(1)用树状图或列表等方法列出所有可能出现的结果;
(2)求两次摸到的球的颜色不同的概率.
17.一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的
反面是平的.将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是
“兵”面朝下.由于棋子的两面不均匀,为了估计“兵”字面朝上的机会大小,某
实验小组做了棋子下掷实验,实验数据如下表:
(1)请将数据表补充完整:
(2)在图中画出“兵”字面朝上的频率分布折线图:
(3)如果实验继续进行下去,根据上表的数据,这个实验所得频率将逐渐稳定到某
一个数值附近,请你估计该随机事件在每次实验时发生的机会大小.
答案解析
1.【答案】B
【解析】直接根据求概率的公式即可得到结果.
因为抽取1000个进行质量检验,结果发现有10个次品,所以从中抽取一个是次品的概率约为,
故选B.
2.【答案】D
【解析】∵硬币只有正反两面,
∴投掷时正面朝上的概率为,
根据频率的概念可知投掷次数逐渐增加,P稳定在附近,
故选D.
3.【答案】A.
【解析】根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.因此,
∵袋子中球的总数为2+3=5,红球有3个,∴摸出红球的概率为.故选A.
4.【答案】B
【解析】在同样的条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,列出方程求解.解
解:由题意得,×100%=20%,
解得,a=15.
故选B.
5.【答案】A
【解析】红红和娜娜玩“锤子、剪刀、布”游戏,所有可能出现的结果列表如下:
由表格可知,共有9种等可能情况.其中平局的有3种:(锤子,锤子)、(剪刀,剪刀)、(布,布).因此,红红和娜娜两人出相同手势的概率为,两人获胜的概率都为,红红不是胜就是输,所以红红胜的概率为,错误,故选项A符合题意,故选项B,C,D不合题意;故选A.
6.【答案】D
【解析】利用“大量重复试验中,事件发生的频率逐渐稳定到某个常数附近,这个常数可以估计事件发生的概率”.连续抛掷2n次不一定正好正面向上和反面向上的次数各一半,故A、B、C错误,
抛掷n次,当n越来越大时,正面朝上的频率会越来越稳定于0.5,故D正确.
故选D.
7.【答案】D
【解析】根据题意得=30%,解得n=30,所以这个不透明的盒子里大约有30个除颜色外其他完全相同的小球.
故选D.
8.【答案】15.
【解析】利用频率估计概率得到摸到白球的概率为0.3,然后根据概率公式计算即可.
解:设袋子中白球有x个,根据题意,得:=0.30,解得:x=15,即布袋中白球可能有15个,故答案为:15.
9.【答案】
【解析】根据几何概率的求法:飞镖落在阴影部分的概率就是阴影区域的面积与总面积的比值.
∵总面积为3×3=9,其中阴影部分面积为4××1×2=4,
∴飞镖落在阴影部分的概率是,
故答案为:.
10.【答案】.
【解析】设其中一双鞋分别为a,a′;另一双鞋分别为b,b′,然后根据题意画树状图,由树状图即可求得所有等可能的结果与恰好能配成一双的情况,再利用概率公式即可求得答案.
设其中一双鞋分别为a,a′;另一双鞋分别为b,b′.
画树状图得:
∵共有12种等可能的结果,恰好能配成一双的有4种情况,
∴恰好能配成一双的概率是:=,
故答案为:.
11.【答案】0.4
【解析】根据各小组频数之和等于数据总和,即可求出第四组的频数,再根据频率=频数÷总数,进行计算.
解:根据题意,得:x=50-3-7-14-6=20,
∴第四组的频率为:.
故答案为:0.4.
12.【答案】3.
【解析】设绿球的个数为x,根据题意,得:=0.2,解得:x=3,经检验x=3是原分式方程的解,即袋中有绿球3个,故答案为:3.
13.【答案】
【解析】设其中一双鞋分别为a,a′;画出树状图,可知共有12种情况,能配成一双的有8种情况,根据概率公式计算即可;
设其中一双鞋分别为a,a′.画树状图得:
∵共有12种情况,能配成一双的有8种情况,∴取出两只刚好配一双鞋的概率是:.
故答案为:.
14.【答案】
【解析】先利用树状图列出两次取出的小球标号和的所有可能情况数,再找出两次取出的小球标号的和等于5的情况数,最后求出概率即可.
两次取出的小球标号和的所有可能情况共有16种,其中和为5的情况有4种,故两次取出的小球标号的和等于5的概率是4÷16=.故答案为.
15.【答案】②③
【解析】根据随机事件发生的“频率”与“概率”的关系进行分析解答即可.
(1)由表中的数据可知,当实验种子数量为100时,两种种子的发芽率虽然都是96%,但结合后续实验数据可知,此时的发芽率并不稳定,故不能确定两种种子发芽的概率就是96%,所以①中的说法不合理;
(2)由表中数据可知,随着实验次数的增加,A种种子发芽的频率逐渐稳定在98%左右,故可以估计A种种子发芽的概率是98%,所以②中的说法是合理的;
(3)由表中数据可知,随着实验次数的增加,A种种子发芽的频率逐渐稳定在98%左右,而B种种子发芽的频率稳定在97%左右,故可以估计在相同条件下,A种种子发芽率大于B种种子发芽率,所以③中的说法是合理的.
故答案为:②③.
16.【答案】(1)详见解析;(2).
【解析】(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由(1)中树状图可求得两次摸到的球的颜色不同的情况有4种,再利用概率公式求解即可求得答案.
(1)如图:
,
所有可能的结果为(白1,白2)、(白1,红)、(白2,白1)、(白2,红)、(红,白1)、(红,白2);
(2)共有6种情况,两次摸到的球的颜色不同的情况有4种,概率为.
17.【答案】(1)18,0.55;(2)见详解;(3)0.55
【解析】(1)根据图中信息,用频数除以实验次数,得到频率,由于试验次数较多,可以用频率估计概率;
(2)将频率作为纵坐标,试验次数作为横坐标,描点连线,可得折线图.
(3)根据表中数据,试验频率为0.7,0.45,0.63,0.59,0.52,0.55,0.56,0.55稳定在0.55左右,即可估计概率的大小.
解:(1)所填数字为:40×0.45=18,66÷120=0.55;
故答案为:18,0.55;
(2)折线图如下:
(3)根据表中数据,试验频率为0.7,0.45,0.63,0.59,0.52,0.55,0.56,0.55稳定在0.55左右,
故估计概率的大小为:0.55.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
