2020-2021学年七年级数学北师大版下册:第四章三角形单元测试题(word版,含答案)
文档属性
| 名称 | 2020-2021学年七年级数学北师大版下册:第四章三角形单元测试题(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 150.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-03 00:00:00 | ||
图片预览


文档简介
第四章 三角形
一、选择题(本大题共8小题,每小题4分,共32分)
1.下列长度的三条线段能组成三角形的是
( )
A.1,2,3.5
B.4,5,9
C.20,15,8
D.5,15,8
2.下列图形中,AD是△ABC的高的是
( )
图4-Z-1
3.若一个三角形三个内角的度数之比为2∶3∶4,则这个三角形是
( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
4.如图4-Z-2,△ABC的面积为8,AD为BC边上的中线,E为AD上任意一点,连接BE,CE,图中阴影部分的面积为
( )
图4-Z-2
A.2
B.3
C.4
D.5
5.如图4-Z-3,在△ABC和△DEC中,AB=DE.若添加条件后使得△ABC≌△DEC,则在下列条件中,不能添加的是
( )
图4-Z-3
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.∠B=∠E,∠A=∠D
D.BC=EC,∠A=∠D
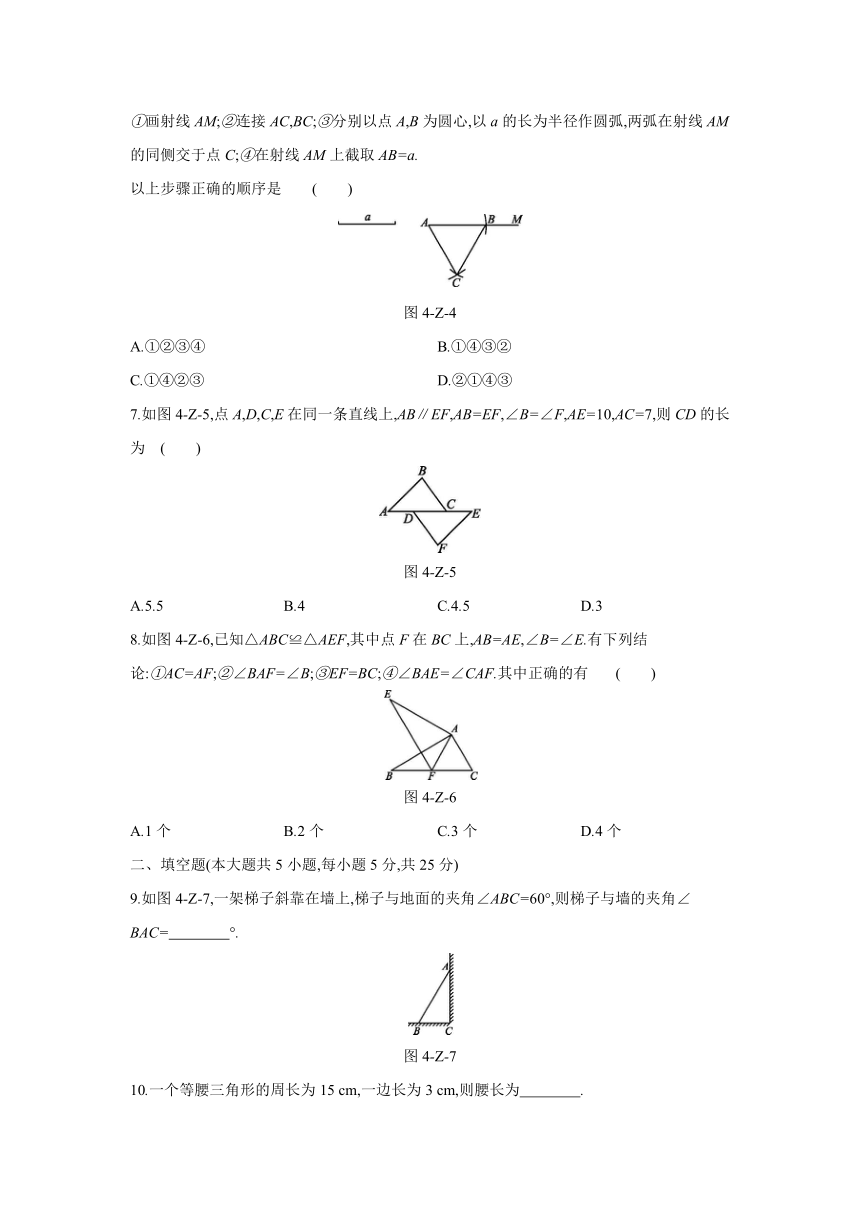
6.如图4-Z-4,已知一条线段的长度为a,求作边长为a的等边三角形,以下是打乱的作图步骤:
①画射线AM;②连接AC,BC;③分别以点A,B为圆心,以a的长为半径作圆弧,两弧在射线AM的同侧交于点C;④在射线AM上截取AB=a.
以上步骤正确的顺序是
( )
图4-Z-4
A.①②③④
B.①④③②
C.①④②③
D.②①④③
7.如图4-Z-5,点A,D,C,E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=7,则CD的长为
( )
图4-Z-5
A.5.5
B.4
C.4.5
D.3
8.如图4-Z-6,已知△ABC≌△AEF,其中点F在BC上,AB=AE,∠B=∠E.有下列结论:①AC=AF;②∠BAF=∠B;③EF=BC;④∠BAE=∠CAF.其中正确的有
( )
图4-Z-6
A.1个
B.2个
C.3个
D.4个
二、填空题(本大题共5小题,每小题5分,共25分)
9.如图4-Z-7,一架梯子斜靠在墙上,梯子与地面的夹角∠ABC=60°,则梯子与墙的夹角∠BAC= °.?
图4-Z-7
10.一个等腰三角形的周长为15
cm,一边长为3
cm,则腰长为 .?
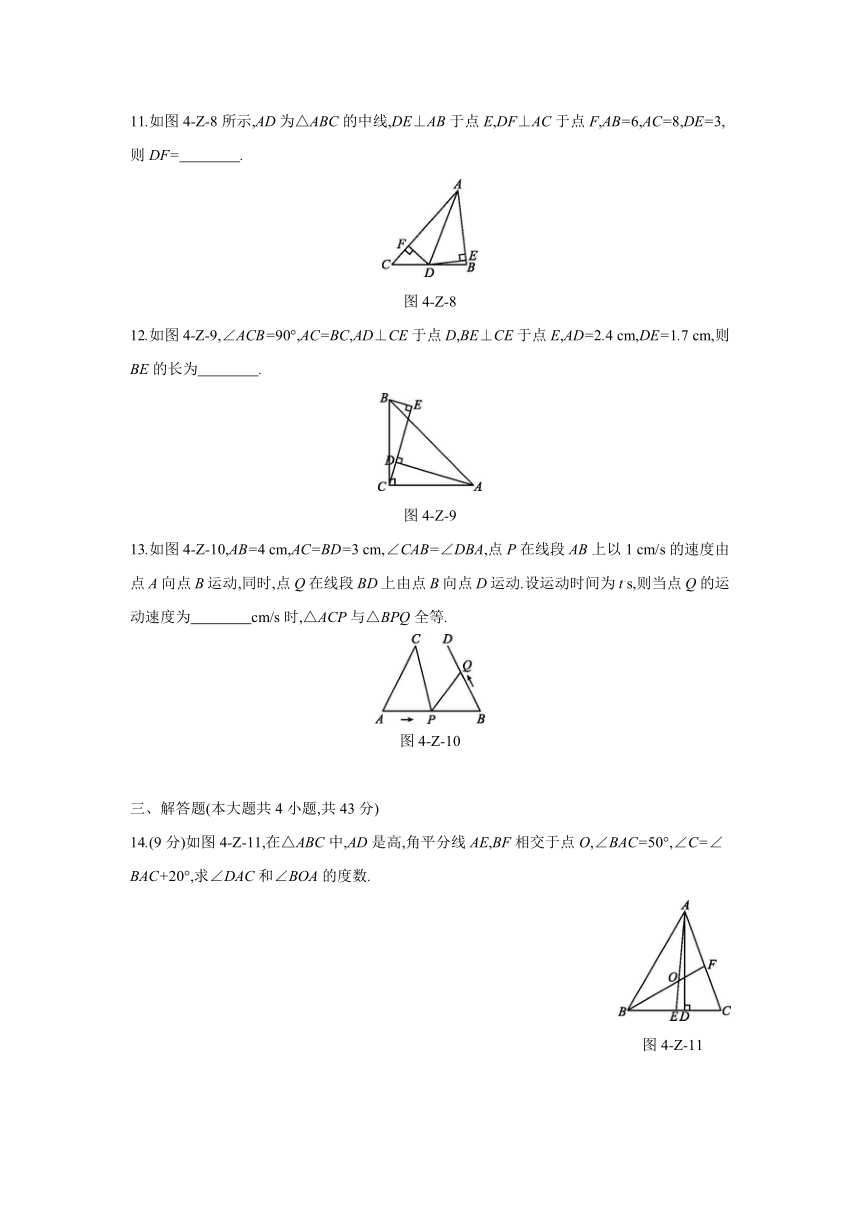
11.如图4-Z-8所示,AD为△ABC的中线,DE⊥AB于点E,DF⊥AC于点F,AB=6,AC=8,DE=3,则DF= .?
图4-Z-8
12.如图4-Z-9,∠ACB=90°,AC=BC,AD⊥CE于点D,BE⊥CE于点E,AD=2.4
cm,DE=1.7
cm,则BE的长为 .?
图4-Z-9
13.如图4-Z-10,AB=4
cm,AC=BD=3
cm,∠CAB=∠DBA,点P在线段AB上以1
cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.设运动时间为t
s,则当点Q的运动速度为 cm/s时,△ACP与△BPQ全等.
图4-Z-10
?
三、解答题(本大题共4小题,共43分)
14.(9分)如图4-Z-11,在△ABC中,AD是高,角平分线AE,BF相交于点O,∠BAC=50°,∠C=∠BAC+20°,求∠DAC和∠BOA的度数.
图4-Z-11
15.(10分)如图4-Z-12,已知在△ABC和△AEF中,AB=AC,AE=AF,∠CAB=∠EAF,BE交FC于点O,交AC于点D.
(1)试说明:BE=CF;
(2)当∠BAC=70°时,求∠BOC的度数.
图4-Z-12
16.(12分)七年级(2)班的篮球啦啦队为了在明天的比赛中给同学们加油助威,每人提前制作了一面同一规格的三角形彩旗.小贝放学回家后,发现自己的彩旗破损了一角(如图4-Z-13①),她想用彩纸重新制作一面彩旗.
(1)请你帮助小贝,用直尺与圆规在彩纸上(如图②)作出一个与破损前完全一样的三角形(不写作法,保留作图痕迹);
(2)你作图的理由是判定三角形全等条件中的“ ”.?
图4-Z-13
17.(12分)如图4-Z-14所示,已知CE⊥AB于点E,BD⊥AC于点D,BD与CE交于点O,且AO平分∠BAC.
(1)图中有多少对全等三角形?请你一一列举出来(不要求说明理由).
(2)小明说:欲说明BE=CD,可先说明△AOE≌△AOD得到AE=AD,再说明△ADB≌△AEC得到AB=AC,然后利用等式的性质即可得到BE=CD,请问他的说法正确吗?如果不正确,请说明理由;如果正确,请按他的思路写出推导过程.
(3)要得到BE=CD,你还有其他的思路吗?请仿照小明的说法具体说一说你的想法.
图4-Z-14
教师详解详析
1.[解析]
C 利用三角形的三边关系判断.
2.D
3.[解析]
B 因为三个内角度数之比为2∶3∶4,所以三个角为40°,60°,80°,所以这个三角形为锐角三角形.故选B.
4.C
5.[解析]
D A项,添加BC=EC,∠B=∠E可用SAS判定两个三角形全等;B项,添加BC=EC,AC=DC可用SSS判定两个三角形全等;C项,添加∠B=∠E,∠A=∠D可用ASA判定两个三角形全等;D项,添加BC=EC,∠A=∠D后是SSA,无法判定三角形全等.故选D.
6.B
7.[解析]
B 因为AB∥EF,所以∠A=∠E.在△ABC和△EFD中,因为∠A=∠E,AB=EF,∠B=∠F,所以△ABC≌△EFD(ASA),所以AC=ED=7,所以AD=AE-ED=10-7=3,所以CD=AC-AD=7-3=4.故选B.
8.C
9.30 10.6
cm
11.
12.0.7
cm
13.1或1.5
14.解:因为∠BAC=50°,∠C=∠BAC+20°,
所以∠C=70°.
因为AD是△ABC的高,
所以AD⊥BC,
所以∠ADC=90°,
所以∠DAC=180°-∠C-∠ADC=20°.
因为∠BAC=50°,∠C=70°,
所以∠ABC=180°-∠BAC-∠C=60°.
因为AE,BF是△ABC的角平分线,
所以∠BAE=∠BAC=25°,∠ABF=∠ABC=30°,
所以∠BOA=180°-∠BAE-∠ABF=180°-25°-30°=125°.
15.解:(1)因为∠CAB=∠EAF,
所以∠CAB+∠CAE=∠EAF+∠CAE,
即∠BAE=∠CAF.
在△BAE和△CAF中,
因为AB=AC,∠BAE=∠CAF,AE=AF,
所以△BAE≌△CAF(SAS),
所以BE=CF.
(2)因为△BAE≌△CAF,
所以∠EBA=∠FCA,即∠DBA=∠OCD.
又因为∠BDA=∠ODC,
所以∠BAD=∠COD.
因为∠BAC=70°,所以∠COD=70°,
即∠BOC=70°.
16.解:(1)如图中的△ABC.
(2)ASA
17.解:(1)4对,分别是△AOE≌△AOD,△BOE≌△COD,△AOB≌△AOC,△ABD≌△ACE.
(2)正确.
因为CE⊥AB于点E,BD⊥AC于点D,
所以∠AEO=∠ADO=90°.
因为AO平分∠BAC,
所以∠OAE=∠OAD.
在△AOE和△AOD中,因为∠AEO=∠ADO,∠OAE=∠OAD,AO=AO,
所以△AOE≌△AOD,
所以AE=AD.
在△ADB和△AEC中,
因为∠BAD=∠CAE,AD=AE,∠ADB=∠AEC,
所以△ADB≌△AEC,所以AB=AC,
所以AB-AE=AC-AD,即BE=CD.
(3)答案不唯一,如可先说明△AOE≌△AOD,得到OE=OD,再说明△BOE≌△COD,得到BE=CD.
一、选择题(本大题共8小题,每小题4分,共32分)
1.下列长度的三条线段能组成三角形的是
( )
A.1,2,3.5
B.4,5,9
C.20,15,8
D.5,15,8
2.下列图形中,AD是△ABC的高的是
( )
图4-Z-1
3.若一个三角形三个内角的度数之比为2∶3∶4,则这个三角形是
( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
4.如图4-Z-2,△ABC的面积为8,AD为BC边上的中线,E为AD上任意一点,连接BE,CE,图中阴影部分的面积为
( )
图4-Z-2
A.2
B.3
C.4
D.5
5.如图4-Z-3,在△ABC和△DEC中,AB=DE.若添加条件后使得△ABC≌△DEC,则在下列条件中,不能添加的是
( )
图4-Z-3
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.∠B=∠E,∠A=∠D
D.BC=EC,∠A=∠D
6.如图4-Z-4,已知一条线段的长度为a,求作边长为a的等边三角形,以下是打乱的作图步骤:
①画射线AM;②连接AC,BC;③分别以点A,B为圆心,以a的长为半径作圆弧,两弧在射线AM的同侧交于点C;④在射线AM上截取AB=a.
以上步骤正确的顺序是
( )
图4-Z-4
A.①②③④
B.①④③②
C.①④②③
D.②①④③
7.如图4-Z-5,点A,D,C,E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=7,则CD的长为
( )
图4-Z-5
A.5.5
B.4
C.4.5
D.3
8.如图4-Z-6,已知△ABC≌△AEF,其中点F在BC上,AB=AE,∠B=∠E.有下列结论:①AC=AF;②∠BAF=∠B;③EF=BC;④∠BAE=∠CAF.其中正确的有
( )
图4-Z-6
A.1个
B.2个
C.3个
D.4个
二、填空题(本大题共5小题,每小题5分,共25分)
9.如图4-Z-7,一架梯子斜靠在墙上,梯子与地面的夹角∠ABC=60°,则梯子与墙的夹角∠BAC= °.?
图4-Z-7
10.一个等腰三角形的周长为15
cm,一边长为3
cm,则腰长为 .?
11.如图4-Z-8所示,AD为△ABC的中线,DE⊥AB于点E,DF⊥AC于点F,AB=6,AC=8,DE=3,则DF= .?
图4-Z-8
12.如图4-Z-9,∠ACB=90°,AC=BC,AD⊥CE于点D,BE⊥CE于点E,AD=2.4
cm,DE=1.7
cm,则BE的长为 .?
图4-Z-9
13.如图4-Z-10,AB=4
cm,AC=BD=3
cm,∠CAB=∠DBA,点P在线段AB上以1
cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.设运动时间为t
s,则当点Q的运动速度为 cm/s时,△ACP与△BPQ全等.
图4-Z-10
?
三、解答题(本大题共4小题,共43分)
14.(9分)如图4-Z-11,在△ABC中,AD是高,角平分线AE,BF相交于点O,∠BAC=50°,∠C=∠BAC+20°,求∠DAC和∠BOA的度数.
图4-Z-11
15.(10分)如图4-Z-12,已知在△ABC和△AEF中,AB=AC,AE=AF,∠CAB=∠EAF,BE交FC于点O,交AC于点D.
(1)试说明:BE=CF;
(2)当∠BAC=70°时,求∠BOC的度数.
图4-Z-12
16.(12分)七年级(2)班的篮球啦啦队为了在明天的比赛中给同学们加油助威,每人提前制作了一面同一规格的三角形彩旗.小贝放学回家后,发现自己的彩旗破损了一角(如图4-Z-13①),她想用彩纸重新制作一面彩旗.
(1)请你帮助小贝,用直尺与圆规在彩纸上(如图②)作出一个与破损前完全一样的三角形(不写作法,保留作图痕迹);
(2)你作图的理由是判定三角形全等条件中的“ ”.?
图4-Z-13
17.(12分)如图4-Z-14所示,已知CE⊥AB于点E,BD⊥AC于点D,BD与CE交于点O,且AO平分∠BAC.
(1)图中有多少对全等三角形?请你一一列举出来(不要求说明理由).
(2)小明说:欲说明BE=CD,可先说明△AOE≌△AOD得到AE=AD,再说明△ADB≌△AEC得到AB=AC,然后利用等式的性质即可得到BE=CD,请问他的说法正确吗?如果不正确,请说明理由;如果正确,请按他的思路写出推导过程.
(3)要得到BE=CD,你还有其他的思路吗?请仿照小明的说法具体说一说你的想法.
图4-Z-14
教师详解详析
1.[解析]
C 利用三角形的三边关系判断.
2.D
3.[解析]
B 因为三个内角度数之比为2∶3∶4,所以三个角为40°,60°,80°,所以这个三角形为锐角三角形.故选B.
4.C
5.[解析]
D A项,添加BC=EC,∠B=∠E可用SAS判定两个三角形全等;B项,添加BC=EC,AC=DC可用SSS判定两个三角形全等;C项,添加∠B=∠E,∠A=∠D可用ASA判定两个三角形全等;D项,添加BC=EC,∠A=∠D后是SSA,无法判定三角形全等.故选D.
6.B
7.[解析]
B 因为AB∥EF,所以∠A=∠E.在△ABC和△EFD中,因为∠A=∠E,AB=EF,∠B=∠F,所以△ABC≌△EFD(ASA),所以AC=ED=7,所以AD=AE-ED=10-7=3,所以CD=AC-AD=7-3=4.故选B.
8.C
9.30 10.6
cm
11.
12.0.7
cm
13.1或1.5
14.解:因为∠BAC=50°,∠C=∠BAC+20°,
所以∠C=70°.
因为AD是△ABC的高,
所以AD⊥BC,
所以∠ADC=90°,
所以∠DAC=180°-∠C-∠ADC=20°.
因为∠BAC=50°,∠C=70°,
所以∠ABC=180°-∠BAC-∠C=60°.
因为AE,BF是△ABC的角平分线,
所以∠BAE=∠BAC=25°,∠ABF=∠ABC=30°,
所以∠BOA=180°-∠BAE-∠ABF=180°-25°-30°=125°.
15.解:(1)因为∠CAB=∠EAF,
所以∠CAB+∠CAE=∠EAF+∠CAE,
即∠BAE=∠CAF.
在△BAE和△CAF中,
因为AB=AC,∠BAE=∠CAF,AE=AF,
所以△BAE≌△CAF(SAS),
所以BE=CF.
(2)因为△BAE≌△CAF,
所以∠EBA=∠FCA,即∠DBA=∠OCD.
又因为∠BDA=∠ODC,
所以∠BAD=∠COD.
因为∠BAC=70°,所以∠COD=70°,
即∠BOC=70°.
16.解:(1)如图中的△ABC.
(2)ASA
17.解:(1)4对,分别是△AOE≌△AOD,△BOE≌△COD,△AOB≌△AOC,△ABD≌△ACE.
(2)正确.
因为CE⊥AB于点E,BD⊥AC于点D,
所以∠AEO=∠ADO=90°.
因为AO平分∠BAC,
所以∠OAE=∠OAD.
在△AOE和△AOD中,因为∠AEO=∠ADO,∠OAE=∠OAD,AO=AO,
所以△AOE≌△AOD,
所以AE=AD.
在△ADB和△AEC中,
因为∠BAD=∠CAE,AD=AE,∠ADB=∠AEC,
所以△ADB≌△AEC,所以AB=AC,
所以AB-AE=AC-AD,即BE=CD.
(3)答案不唯一,如可先说明△AOE≌△AOD,得到OE=OD,再说明△BOE≌△COD,得到BE=CD.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
