2020-2021学年七年级数学苏科版下册-8.3 同底数幂的除法-课件(25张)
文档属性
| 名称 | 2020-2021学年七年级数学苏科版下册-8.3 同底数幂的除法-课件(25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
同底数幂的除法(2)
同底数幂的除法法则
(a≠0,m、n都是正整数)
同底数幂相除,底数_____,指数_______
.
不变
相减
am
÷an
=
am-n
am
an
=am-n
你有哪些方法可以来计算下列各式
(1)23÷23
解:①=
2
0
②=1
发现:20___1
=
(2)am÷am
解:①=
a
0
②=1
发现:a0___1
=
规定:a0=1
(其中a≠0)
任何不为0的数的0次幂等于1
你有哪些方法可以来计算下列各式
(1)23÷25
解:①=
2
-2
②=
23
25
=
1
22
=
发现:2-2___
1
22
(2)a0÷ap
(其中a≠0)
解:①=
a
-p
②=
a0
ap
=
1
ap
=
发现:a-p___
1
ap
规定:a-p
=
1
ap
任何不等于0的数的-p次幂,等于这个数的p次幂的倒数。
(其中a≠0)
例1、计算
(1)92÷92
解:=
9
0
=1
(2)(ab)n÷(ab)n
解:=
(ab)
0
=1
(3)(-3)m÷(-3)m
解:=
(-3)
0
=1
例2、用小数或分数表示下列各数
(1)2-3
解:=
1
23
=
1
8
(2)(-3)-2
解:=
1
(-3)2
=
1
9
(3)-3-2
解:=-
1
32
=-
1
9
注意:要分清底数
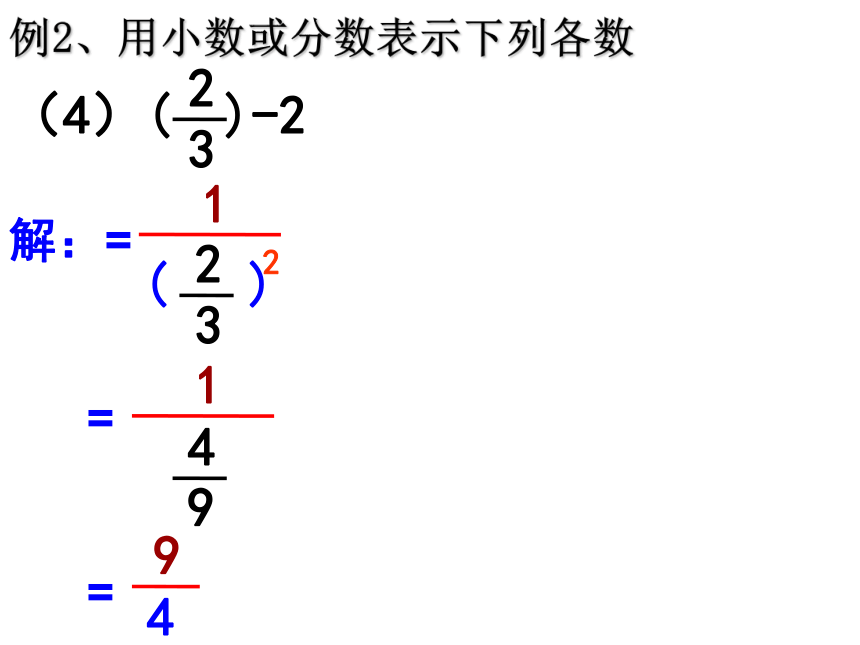
例2、用小数或分数表示下列各数
(4)(
)-2
2
3
解:=
1
(
)
2
2
3
=
1
4
9
=
9
4
规定:a-p
=
1
ap
(其中a≠0)
=
1
a
(a-1)
p
=(
)
p
任何不等于0的数的-p次幂,等于这个数的倒数的p次幂。.
例2、用小数或分数表示下列各数
(4)(
)-2
2
3
方法2:=
2
(
)
2
3
=
9
4
例2、用小数或分数表示下列各数
(4)(
)-2
2
3
解:=
1
(
)
2
2
3
=
1
4
9
=
9
4
方法2:=
2
(
)
2
3
=
9
4
注意:当底数是分数时,选用公式
a-p
1
a
=(
)
p
正指数幂的倒数
倒数的正指数幂
例3、把下列小数或分数写成负整数指数幂的形式。
(1)-
1
8
解:=
23
-
1
=-
2
-3
或=-
8
-1
(2)0.0001
解:=
10000
1
=
104
1
=
10
-4
例3、把下列小数或分数写成负整数指数幂的形式。
(3)
1
64
解:=
43
1
=
4
-3
例4、计算
(1)25
÷2-3×20
解:=25
-(-3)
×1
=28
=256
例4、计算
(2)
×(
)
2
1
2
=
(
)
0
1
2
=1
(3)
解:=
[6-2×
]-2
1
=4-2
=
42
1
=
16
1
练习、计算
(1)-2-2
–(-2)3
解:=-
22
1
-
(-8)
=-
4
1
+8
=7
4
3
练习、计算
(2)(-3)-3
+(-3)0
解:=
+1
(-3)3
1
=
-27
1
+1
=
27
26
(3)
y-6﹒y12÷[(-y)2]-3
=
y6
÷[y2]-3
=
y6
÷y-6
=
y12
例题解析
1、用分数或小数表示下列各数
(5)-2.7×10-2
解:=-2.7×
102
1
=-2.7×
100
1
=-2.7×
0.01
=-0.027
4、计算
(1)
=1
+10
2
+
1000
1
=101
1000
1
5、(1)若(x+2)0无意义,则x的取值是____
a0=1
(其中a≠0)
a0有意义
a0
(其中a=0)
a0无意义
∴x+2=0
x=-2
-2
5、(2)若∣
x∣
=(x-1)0,则x=____
∴x=±1
解:∣x∣=1
∴x≠1
∵x-1≠0
∴x=-1
-1
填空
(2)
,
则x=___.
(3)256b=25×211,则b=__.
(5)若0.0000003=3×10m,则m=___.
-5
2
-2
-7
(1)
107=________
,10-5=________.
10000000
0.00001
同底数幂的除法(2)
同底数幂的除法法则
(a≠0,m、n都是正整数)
同底数幂相除,底数_____,指数_______
.
不变
相减
am
÷an
=
am-n
am
an
=am-n
你有哪些方法可以来计算下列各式
(1)23÷23
解:①=
2
0
②=1
发现:20___1
=
(2)am÷am
解:①=
a
0
②=1
发现:a0___1
=
规定:a0=1
(其中a≠0)
任何不为0的数的0次幂等于1
你有哪些方法可以来计算下列各式
(1)23÷25
解:①=
2
-2
②=
23
25
=
1
22
=
发现:2-2___
1
22
(2)a0÷ap
(其中a≠0)
解:①=
a
-p
②=
a0
ap
=
1
ap
=
发现:a-p___
1
ap
规定:a-p
=
1
ap
任何不等于0的数的-p次幂,等于这个数的p次幂的倒数。
(其中a≠0)
例1、计算
(1)92÷92
解:=
9
0
=1
(2)(ab)n÷(ab)n
解:=
(ab)
0
=1
(3)(-3)m÷(-3)m
解:=
(-3)
0
=1
例2、用小数或分数表示下列各数
(1)2-3
解:=
1
23
=
1
8
(2)(-3)-2
解:=
1
(-3)2
=
1
9
(3)-3-2
解:=-
1
32
=-
1
9
注意:要分清底数
例2、用小数或分数表示下列各数
(4)(
)-2
2
3
解:=
1
(
)
2
2
3
=
1
4
9
=
9
4
规定:a-p
=
1
ap
(其中a≠0)
=
1
a
(a-1)
p
=(
)
p
任何不等于0的数的-p次幂,等于这个数的倒数的p次幂。.
例2、用小数或分数表示下列各数
(4)(
)-2
2
3
方法2:=
2
(
)
2
3
=
9
4
例2、用小数或分数表示下列各数
(4)(
)-2
2
3
解:=
1
(
)
2
2
3
=
1
4
9
=
9
4
方法2:=
2
(
)
2
3
=
9
4
注意:当底数是分数时,选用公式
a-p
1
a
=(
)
p
正指数幂的倒数
倒数的正指数幂
例3、把下列小数或分数写成负整数指数幂的形式。
(1)-
1
8
解:=
23
-
1
=-
2
-3
或=-
8
-1
(2)0.0001
解:=
10000
1
=
104
1
=
10
-4
例3、把下列小数或分数写成负整数指数幂的形式。
(3)
1
64
解:=
43
1
=
4
-3
例4、计算
(1)25
÷2-3×20
解:=25
-(-3)
×1
=28
=256
例4、计算
(2)
×(
)
2
1
2
=
(
)
0
1
2
=1
(3)
解:=
[6-2×
]-2
1
=4-2
=
42
1
=
16
1
练习、计算
(1)-2-2
–(-2)3
解:=-
22
1
-
(-8)
=-
4
1
+8
=7
4
3
练习、计算
(2)(-3)-3
+(-3)0
解:=
+1
(-3)3
1
=
-27
1
+1
=
27
26
(3)
y-6﹒y12÷[(-y)2]-3
=
y6
÷[y2]-3
=
y6
÷y-6
=
y12
例题解析
1、用分数或小数表示下列各数
(5)-2.7×10-2
解:=-2.7×
102
1
=-2.7×
100
1
=-2.7×
0.01
=-0.027
4、计算
(1)
=1
+10
2
+
1000
1
=101
1000
1
5、(1)若(x+2)0无意义,则x的取值是____
a0=1
(其中a≠0)
a0有意义
a0
(其中a=0)
a0无意义
∴x+2=0
x=-2
-2
5、(2)若∣
x∣
=(x-1)0,则x=____
∴x=±1
解:∣x∣=1
∴x≠1
∵x-1≠0
∴x=-1
-1
填空
(2)
,
则x=___.
(3)256b=25×211,则b=__.
(5)若0.0000003=3×10m,则m=___.
-5
2
-2
-7
(1)
107=________
,10-5=________.
10000000
0.00001
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
