2020-2021学年人教版 八年级数学下册知识讲义-18.1平行四边形-平行四边形的性质含答案
文档属性
| 名称 | 2020-2021学年人教版 八年级数学下册知识讲义-18.1平行四边形-平行四边形的性质含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 118.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 00:00:00 | ||
图片预览



文档简介
初中数学
平行四边形的性质
精讲精练
【考点精讲】
平行四边形的性质
边
平行四边形的对边互相平行;平行四边形的对边相等
角
平行四边形的邻角互补;平行四边形的对角相等
对角线
平行四边形的对角线互相平分
【典例精析】
例题1
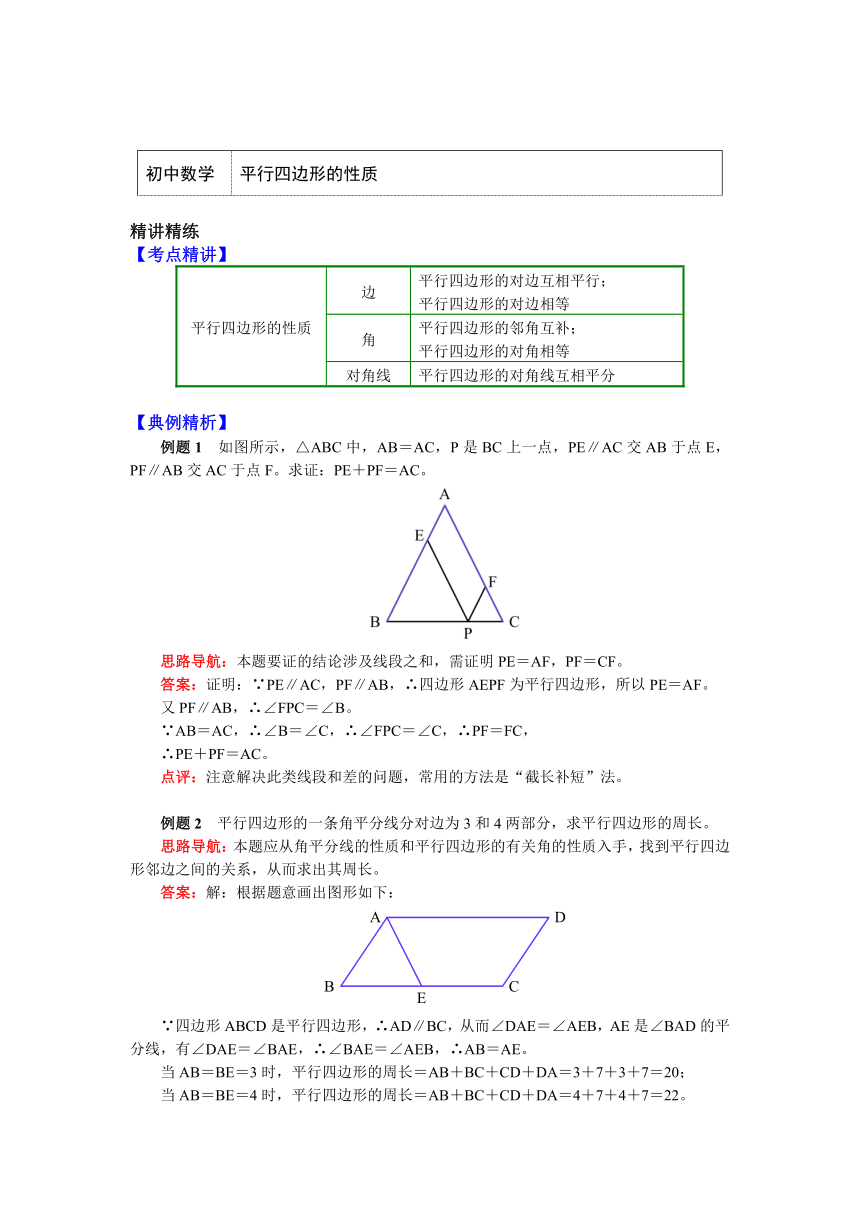
如图所示,△ABC中,AB=AC,P是BC上一点,PE∥AC交AB于点E,PF∥AB交AC于点F。求证:PE+PF=AC。
思路导航:本题要证的结论涉及线段之和,需证明PE=AF,PF=CF。
答案:证明:∵PE∥AC,PF∥AB,∴四边形AEPF为平行四边形,所以PE=AF。
又PF∥AB,∴∠FPC=∠B。
∵AB=AC,∴∠B=∠C,∴∠FPC=∠C,∴PF=FC,
∴PE+PF=AC。
点评:注意解决此类线段和差的问题,常用的方法是“截长补短”法。
例题2
平行四边形的一条角平分线分对边为3和4两部分,求平行四边形的周长。
思路导航:本题应从角平分线的性质和平行四边形的有关角的性质入手,找到平行四边形邻边之间的关系,从而求出其周长。
答案:解:根据题意画出图形如下:
∵四边形ABCD是平行四边形,∴AD∥BC,从而∠DAE=∠AEB,AE是∠BAD的平分线,有∠DAE=∠BAE,∴∠BAE=∠AEB,∴AB=AE。
当AB=BE=3时,平行四边形的周长=AB+BC+CD+DA=3+7+3+7=20;
当AB=BE=4时,平行四边形的周长=AB+BC+CD+DA=4+7+4+7=22。
综上所述,平行四边形的周长是20或22.
点评:本题并没有明确指出被角平分线分成两部分的对边中哪条线段等于3,哪条线段等于4,所以可能存在多个解,应分类讨论。解答此类问题时考虑要全面,分析要深入,以免漏解。
例题3
如图所示,已知平行四边形ABCD,∠EAD=∠BAF。
(1)求证:△CEF是等腰三角形;
(2)问△CEF的哪两边之和恰好等于平行四边形ABCD的周长,说明你的结论。
思路导航:(1)只要证出∠E=∠F,即可得到△CEF为等腰三角形;(2)将平行四边形ABCD的周长转化为△CEF两边之和。
答案:(1)证明:∵四边形ABCD是平行四边形,∴DA∥CF,AB∥CE。∴∠EAD=∠F,∠BAF=∠E。又因为∠EAD=∠BAF,∴∠E=∠F,∴△CEF是等腰三角形。
(2)CE与CF之和恰好等于平行四边形ABCD的周长。
理由:由(1)得∠EAD=∠BAF=∠F=∠E,∴BF=AB,DE=AD,∴CE+CF=CD+AD+CB+AB,即CE+CF等于平行四边形ABCD的周长。
点评:本题综合考查了等腰三角形的性质和平行四边形的性质,这两个性质都能实现线段之间的等量代换,它们是证明线段相等的重要方法。
例题4
如图①所示,四边形ABCD是平行四边形,对角线AC、BD相交于点O,过点O作直线EF分别交AD、BC于点E、F。
(1)求证:OE=OF;
(2)如图②所示,若过O点的直线与BA、DC的延长线分别交于点E、F,你能得到(1)中的结论吗?由此你能得出什么样的一般性结论?
思路导航:应用平行四边形的性质结合全等三角形来证明。
答案:(1)证明:∵四边形ABCD是平行四边形,所以AD∥BC,AO=CO,∴∠EAO=∠FCO。∵∠AOE=∠COF,∴△AOE≌△COF,∴OE=OF。
(2)能得到OE=OF,方法同(1)。一般性结论:经过平行四边形对角线交点的直线被平行四边形的对边或对边延长线截得的线段被平行四边形的对角线的交点平分。
点评:本题主要考查平行四边形的性质、全等三角形的判定和性质。本题中的第(2)问属于结论开放型问题,在总结归纳一般性结论时应围绕OE=OF展开。
【总结提升】
应用平行四边形的性质可以证明线段相等、角相等。因此找到一个平行四边形或构造一个平行四边形,利用平行四边形的对边相等、对角相等来转移边和角,从而把分散的条件集中起来,是本讲知识的创新应用之处。
例题
在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F=__________°。
思路导航:由平行四边形的对角相等、对顶角相等可把∠B转移到△DEF中,使已知的角和所求的角集中在一个三角形中。
答案:∵四边形ABCD是平行四边形,
∴∠ADC=∠B=110°
∵∠FDE=∠ADC=110°
在△EFD中,
∠E+∠F=180°-∠FDE=180°-110°=70°
同步练习
(答题时间:30分钟)
一、选择题
1.
已知□ABCD的周长为32,AB=4,则BC=(
)
A.
4
B.
12
C.
24
D.
28
2.
如图,点A在平行四边形的对角线上,试判断S1,S2之间的大小关系(
)
A.
S1=S2
B.
S1>S2
C.
S1<S2
D.
无法确定
3.
如图,在平行四边形
ABCD中(AB≠BC),直线EF经过其对角线的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:①AO=BO;②OE=OF;
③△EAM≌△FCN;④△EAO≌△CNO,其中正确的是(
)
A.
①②
B.
②③
C.
②④
D.
③④
二、填空题
4.
若平行四边形ABCD的周长为80,相邻两边的长度比为1∶3,则它的四边长为__________。
5.
如图,平行四边形ABCD的对角线交于点O,直线EF过O点且EF∥AD,直线GH过点O且GH∥AB,则能用图中字母表示的平行四边形共有__________个。
6.
如图,在□ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是__________。
三、解答题
7.
如图,已知E、F是□ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC。
(1)求证:△ABE≌△CDF;
(2)请写出图中除△ABE≌△CDF外其余两对全等三角形(不再添加辅助线)。
8.
如图,BD是平行四边形ABCD的对角线,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F。求证:△ABE≌△CDF。
9.
如图,在平行四边形ABCD中,∠BAD=32°。分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF,延长AB交边EC于点G,点G在E、C两点之间,连接AE、AF。
(1)求证:△ABE≌△FDA;
(2)当AE⊥AF时,求∠EBG的度数。
答案
1.
B
解析:BC=(32-2×4)=12。
2.
A
解析:根据平行四边形的性质,S1和S2是同底等高的三角形,其面积相等。
3.
B
解析:根据平行四边形的对角线互相平分不难证明△AOE≌△COF,从而可得出OE=OF,△EAM≌△FCN,即②③是正确的;①④不正确。
4.
10,30,10,30
解析:因为此平行四边形的周长为80,所以一组邻边之和为40,又因为邻边之比为1∶3,所以这组邻边长分别为40×=10,40×=30,所以它的四边长分别为10,30,10,30。
5.
18
解析:本题一定要分类查找,不然很容易重复或漏掉。比如,把平行四边形分成三类:①由AB、BC、CD、DA构成的平行四边形,有1个,即平行四边形ABCD;②不含有以上四条线段或它们的一部分,这样的平行四边形只有1个,是EHFG;③与AE平行且相等的线段有OG、DF、OH,它们都能与AE组成平行四边形,类似地还有BE、BH、HC、CF、FD、DG、AG,共3×8=24个,但这里面有8个重复,所以这类平行四边形有16个。再比如,把平行四边形分成三类,除了外围最大的和内部最小的两个平行四边形,其余的都是由线段AE、GO、DF、BE、OH、CF、AG、OE、BH、OG、OF、CH构成的,我们可以按照类似于数线段条数的方法沿确定的方向逐一判断。
6.
2
解析:∵四边形ABCD是平行四边形,∴AB∥CD,又EF⊥AB,∴EF⊥CD。∵点E是BC的中点,在△BEF和△CEH中,∠BFE=∠CHE=90°,∠BEF=∠CEH,BE=CE,∴△BEF≌△CHE,∴EF=HE,BF=CH。AD=BC=4,在Rt△BEF中,∠ABC=60°,BE=2,∴BF=1,EF=。∴CH=1,又CD=AB=3,∴DH=CD+CH=4,即△EFD的高为DH=4,∴S△DEF=EF·DH=××4=2。
7.
(1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠BAE=∠DCF。又∵BE⊥AC,DF⊥AC,∴∠AEB=∠CFD=90°,∴△ABE≌△CDF(AAS);(2)解:①△ABC≌△CDA,②△BCE≌△DAF。
8.
证明:在平行四边形ABCD中,AB=CD,∠A=∠C,AB∥CD,∴∠ABD=∠CDB,∵∠ABE=∠ABD,∠CDF=∠CDB,∴∠ABE=∠CDF。在△ABE与△CDF中,,∴△ABE≌△CDF。
9.
(1)证明:在平行四边形ABCD中,AB=DC。又∵DF=DC,∴AB=DF。同理EB=AD。在平行四边形ABCD中,∠ABC=∠ADC。又∵∠EBC=∠CDF,∴∠ABE=∠FDA,∴△ABE≌△FDA。(2)解:∵△ABE≌△FDA,∴∠AEB=∠FAD。∵∠EBG=∠AEB+∠EAB,∴∠EBG=∠DAF+∠EAB。∵AE⊥AF,∴∠EAF=90°。∵∠BAD=32°,∴∠DAF+∠EAB=90°-32°=58°,∴∠EBG=58°。
平行四边形的性质
精讲精练
【考点精讲】
平行四边形的性质
边
平行四边形的对边互相平行;平行四边形的对边相等
角
平行四边形的邻角互补;平行四边形的对角相等
对角线
平行四边形的对角线互相平分
【典例精析】
例题1
如图所示,△ABC中,AB=AC,P是BC上一点,PE∥AC交AB于点E,PF∥AB交AC于点F。求证:PE+PF=AC。
思路导航:本题要证的结论涉及线段之和,需证明PE=AF,PF=CF。
答案:证明:∵PE∥AC,PF∥AB,∴四边形AEPF为平行四边形,所以PE=AF。
又PF∥AB,∴∠FPC=∠B。
∵AB=AC,∴∠B=∠C,∴∠FPC=∠C,∴PF=FC,
∴PE+PF=AC。
点评:注意解决此类线段和差的问题,常用的方法是“截长补短”法。
例题2
平行四边形的一条角平分线分对边为3和4两部分,求平行四边形的周长。
思路导航:本题应从角平分线的性质和平行四边形的有关角的性质入手,找到平行四边形邻边之间的关系,从而求出其周长。
答案:解:根据题意画出图形如下:
∵四边形ABCD是平行四边形,∴AD∥BC,从而∠DAE=∠AEB,AE是∠BAD的平分线,有∠DAE=∠BAE,∴∠BAE=∠AEB,∴AB=AE。
当AB=BE=3时,平行四边形的周长=AB+BC+CD+DA=3+7+3+7=20;
当AB=BE=4时,平行四边形的周长=AB+BC+CD+DA=4+7+4+7=22。
综上所述,平行四边形的周长是20或22.
点评:本题并没有明确指出被角平分线分成两部分的对边中哪条线段等于3,哪条线段等于4,所以可能存在多个解,应分类讨论。解答此类问题时考虑要全面,分析要深入,以免漏解。
例题3
如图所示,已知平行四边形ABCD,∠EAD=∠BAF。
(1)求证:△CEF是等腰三角形;
(2)问△CEF的哪两边之和恰好等于平行四边形ABCD的周长,说明你的结论。
思路导航:(1)只要证出∠E=∠F,即可得到△CEF为等腰三角形;(2)将平行四边形ABCD的周长转化为△CEF两边之和。
答案:(1)证明:∵四边形ABCD是平行四边形,∴DA∥CF,AB∥CE。∴∠EAD=∠F,∠BAF=∠E。又因为∠EAD=∠BAF,∴∠E=∠F,∴△CEF是等腰三角形。
(2)CE与CF之和恰好等于平行四边形ABCD的周长。
理由:由(1)得∠EAD=∠BAF=∠F=∠E,∴BF=AB,DE=AD,∴CE+CF=CD+AD+CB+AB,即CE+CF等于平行四边形ABCD的周长。
点评:本题综合考查了等腰三角形的性质和平行四边形的性质,这两个性质都能实现线段之间的等量代换,它们是证明线段相等的重要方法。
例题4
如图①所示,四边形ABCD是平行四边形,对角线AC、BD相交于点O,过点O作直线EF分别交AD、BC于点E、F。
(1)求证:OE=OF;
(2)如图②所示,若过O点的直线与BA、DC的延长线分别交于点E、F,你能得到(1)中的结论吗?由此你能得出什么样的一般性结论?
思路导航:应用平行四边形的性质结合全等三角形来证明。
答案:(1)证明:∵四边形ABCD是平行四边形,所以AD∥BC,AO=CO,∴∠EAO=∠FCO。∵∠AOE=∠COF,∴△AOE≌△COF,∴OE=OF。
(2)能得到OE=OF,方法同(1)。一般性结论:经过平行四边形对角线交点的直线被平行四边形的对边或对边延长线截得的线段被平行四边形的对角线的交点平分。
点评:本题主要考查平行四边形的性质、全等三角形的判定和性质。本题中的第(2)问属于结论开放型问题,在总结归纳一般性结论时应围绕OE=OF展开。
【总结提升】
应用平行四边形的性质可以证明线段相等、角相等。因此找到一个平行四边形或构造一个平行四边形,利用平行四边形的对边相等、对角相等来转移边和角,从而把分散的条件集中起来,是本讲知识的创新应用之处。
例题
在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F=__________°。
思路导航:由平行四边形的对角相等、对顶角相等可把∠B转移到△DEF中,使已知的角和所求的角集中在一个三角形中。
答案:∵四边形ABCD是平行四边形,
∴∠ADC=∠B=110°
∵∠FDE=∠ADC=110°
在△EFD中,
∠E+∠F=180°-∠FDE=180°-110°=70°
同步练习
(答题时间:30分钟)
一、选择题
1.
已知□ABCD的周长为32,AB=4,则BC=(
)
A.
4
B.
12
C.
24
D.
28
2.
如图,点A在平行四边形的对角线上,试判断S1,S2之间的大小关系(
)
A.
S1=S2
B.
S1>S2
C.
S1<S2
D.
无法确定
3.
如图,在平行四边形
ABCD中(AB≠BC),直线EF经过其对角线的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:①AO=BO;②OE=OF;
③△EAM≌△FCN;④△EAO≌△CNO,其中正确的是(
)
A.
①②
B.
②③
C.
②④
D.
③④
二、填空题
4.
若平行四边形ABCD的周长为80,相邻两边的长度比为1∶3,则它的四边长为__________。
5.
如图,平行四边形ABCD的对角线交于点O,直线EF过O点且EF∥AD,直线GH过点O且GH∥AB,则能用图中字母表示的平行四边形共有__________个。
6.
如图,在□ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB,垂足为点F,与DC的延长线相交于点H,则△DEF的面积是__________。
三、解答题
7.
如图,已知E、F是□ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC。
(1)求证:△ABE≌△CDF;
(2)请写出图中除△ABE≌△CDF外其余两对全等三角形(不再添加辅助线)。
8.
如图,BD是平行四边形ABCD的对角线,∠ABD的平分线BE交AD于点E,∠CDB的平分线DF交BC于点F。求证:△ABE≌△CDF。
9.
如图,在平行四边形ABCD中,∠BAD=32°。分别以BC、CD为边向外作△BCE和△DCF,使BE=BC,DF=DC,∠EBC=∠CDF,延长AB交边EC于点G,点G在E、C两点之间,连接AE、AF。
(1)求证:△ABE≌△FDA;
(2)当AE⊥AF时,求∠EBG的度数。
答案
1.
B
解析:BC=(32-2×4)=12。
2.
A
解析:根据平行四边形的性质,S1和S2是同底等高的三角形,其面积相等。
3.
B
解析:根据平行四边形的对角线互相平分不难证明△AOE≌△COF,从而可得出OE=OF,△EAM≌△FCN,即②③是正确的;①④不正确。
4.
10,30,10,30
解析:因为此平行四边形的周长为80,所以一组邻边之和为40,又因为邻边之比为1∶3,所以这组邻边长分别为40×=10,40×=30,所以它的四边长分别为10,30,10,30。
5.
18
解析:本题一定要分类查找,不然很容易重复或漏掉。比如,把平行四边形分成三类:①由AB、BC、CD、DA构成的平行四边形,有1个,即平行四边形ABCD;②不含有以上四条线段或它们的一部分,这样的平行四边形只有1个,是EHFG;③与AE平行且相等的线段有OG、DF、OH,它们都能与AE组成平行四边形,类似地还有BE、BH、HC、CF、FD、DG、AG,共3×8=24个,但这里面有8个重复,所以这类平行四边形有16个。再比如,把平行四边形分成三类,除了外围最大的和内部最小的两个平行四边形,其余的都是由线段AE、GO、DF、BE、OH、CF、AG、OE、BH、OG、OF、CH构成的,我们可以按照类似于数线段条数的方法沿确定的方向逐一判断。
6.
2
解析:∵四边形ABCD是平行四边形,∴AB∥CD,又EF⊥AB,∴EF⊥CD。∵点E是BC的中点,在△BEF和△CEH中,∠BFE=∠CHE=90°,∠BEF=∠CEH,BE=CE,∴△BEF≌△CHE,∴EF=HE,BF=CH。AD=BC=4,在Rt△BEF中,∠ABC=60°,BE=2,∴BF=1,EF=。∴CH=1,又CD=AB=3,∴DH=CD+CH=4,即△EFD的高为DH=4,∴S△DEF=EF·DH=××4=2。
7.
(1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠BAE=∠DCF。又∵BE⊥AC,DF⊥AC,∴∠AEB=∠CFD=90°,∴△ABE≌△CDF(AAS);(2)解:①△ABC≌△CDA,②△BCE≌△DAF。
8.
证明:在平行四边形ABCD中,AB=CD,∠A=∠C,AB∥CD,∴∠ABD=∠CDB,∵∠ABE=∠ABD,∠CDF=∠CDB,∴∠ABE=∠CDF。在△ABE与△CDF中,,∴△ABE≌△CDF。
9.
(1)证明:在平行四边形ABCD中,AB=DC。又∵DF=DC,∴AB=DF。同理EB=AD。在平行四边形ABCD中,∠ABC=∠ADC。又∵∠EBC=∠CDF,∴∠ABE=∠FDA,∴△ABE≌△FDA。(2)解:∵△ABE≌△FDA,∴∠AEB=∠FAD。∵∠EBG=∠AEB+∠EAB,∴∠EBG=∠DAF+∠EAB。∵AE⊥AF,∴∠EAF=90°。∵∠BAD=32°,∴∠DAF+∠EAB=90°-32°=58°,∴∠EBG=58°。
