2020-2021学年人教版八年级数学下册 19.1.1变量与函数(20张)
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册 19.1.1变量与函数(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1006.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 15:46:56 | ||
图片预览







文档简介
(共20张PPT)
19.1.1变量与常量
目标1.
结合具体事例能理解变量与常量的概念,会指出变化中的变量与常量
1.票房收入问题:每张电影票的售价为10元.
(1)若一场售出150张电影票,则该场的票房收入
是
元;
(2)若一场售出205张电影票,则该场的票房收入
是
元;
(3)若设一场售出x张电影票,票房收入为
y元,则
y=
。
小结:票房收入随售出的电影票数变化而变化,即
y随
的变化而变化;
2.行程问题:汽车以60千米/小时的速度匀速行驶,行驶里程为s千米,行驶时间为t小时.请根据题意填表:
小结:行驶路程随
的变化而变化,有关系式s=
,即s随
的变化而变化;
t(时)
1
2
3
…
10
S(千米)
1500
2050
10x
x
60
120
180
600
时间
60t
t
目标1.结合具体事例能理解变量与常量的概念,并会指出变化中的变量与常量
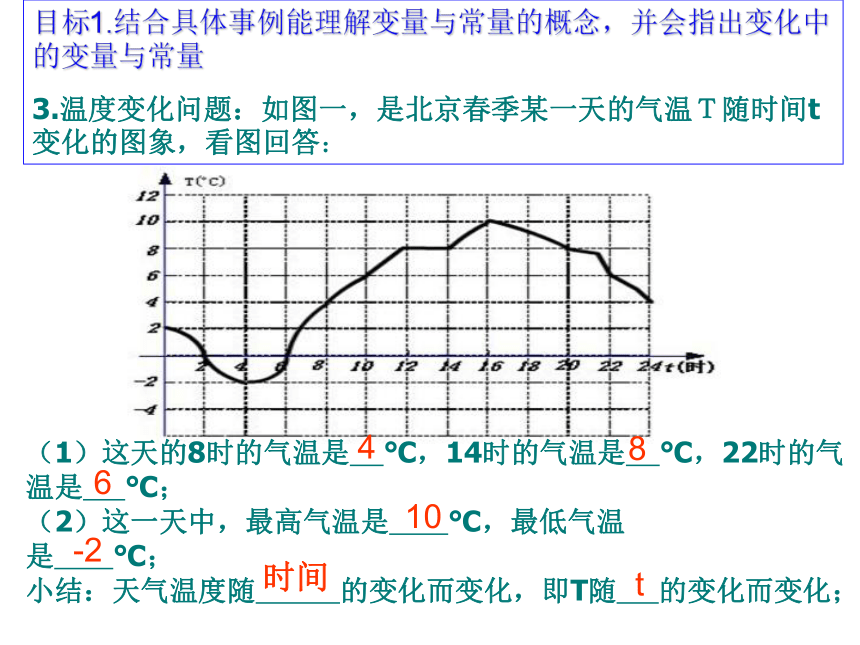
3.温度变化问题:如图一,是北京春季某一天的气温T随时间t变化的图象,看图回答:
(1)这天的8时的气温是
℃,14时的气温是
℃,22时的气温是
℃;
(2)这一天中,最高气温是
℃,最低气温
是
℃;
小结:天气温度随
的变化而变化,即T随
的变化而变化;
4
8
6
10
-2
时间
t
在上面的问题反映了不同事物的变化过程,其中有些量(例如售出票数x,票房收入y;时间t,路程s……)的值按照某种规律
,有些量的值始终
(例如电影票的单价10元……)。
变化
不变
目标1.结合具体事例能理解变量与常量的概念,并会指出变化中的变量与常量
二、问题引申:
常量、变量的概念:
在一个变化过程中:发生变化的量叫做
;不变的量叫做
;
指出前面三个问题中的常量、变量.
(1)“票房收入问题”中y=10x,常量是
,变量是
;
(2)“行程问题”中s=60t,常量是
,变量是
;
(3)“气温变化问题”,
变量是
;
变量
常量
10
x和y
60
t和s
t和T
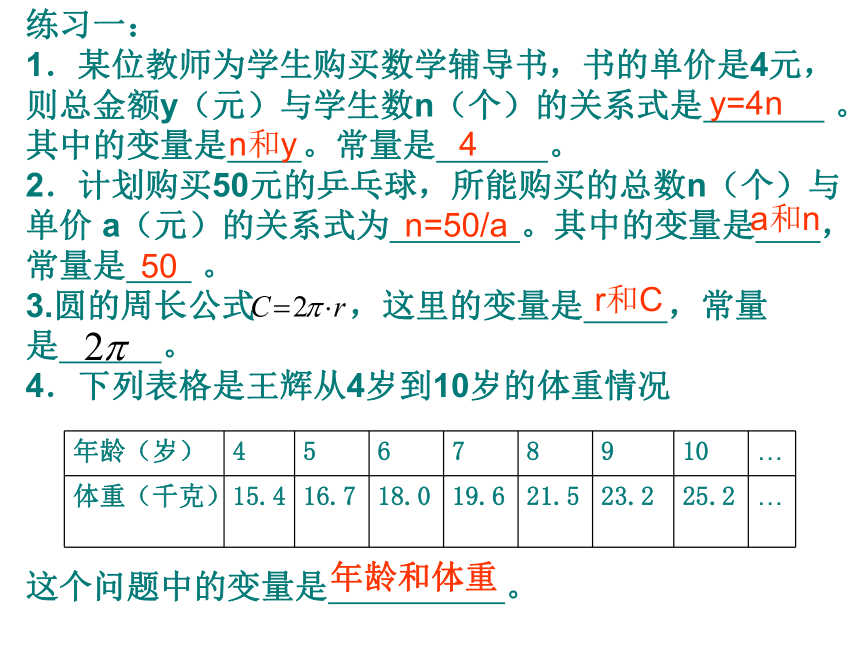
练习一:
1.某位教师为学生购买数学辅导书,书的单价是4元,则总金额y(元)与学生数n(个)的关系式是
。其中的变量是
。常量是
。
2.计划购买50元的乒乓球,所能购买的总数n(个)与单价
a(元)的关系式为
。其中的变量是
,常量是
。
3.圆的周长公式
,这里的变量是
,常量是
。
4.下列表格是王辉从4岁到10岁的体重情况
这个问题中的变量是
。
年龄(岁)
4
5
6
7
8
9
10
…
体重(千克)
15.4
16.7
18.0
19.6
21.5
23.2
25.2
…
y=4n
n和y
4
n=50/a
a和n
50
r和C
年龄和体重
想一想:
在学习了变量之后,我们会发现两个变量的变化并不是孤立地发生,而是存在一些互相联系,你能说出它是什么吗?
目标2.掌握函数的概念,会判断两个变量的关系是否可看作函数,
以上所举变化过程中,两个变量之间的对应关系都满足:对于一个变量取定一个值时,另一个变量就有唯一确定的值与其对应.
例如:若一场售出150张电影票,则该场的票房收入是
1500
元
若一场售出205张电影票,则该场的票房收入
是
2050
元;
1、函数的概念
目标2.掌握函数的概念,会判断两个变量
的关系是否可看作函数
一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值。
2.自变量、函数、函数值:
指出前面三个问题中的自变量与函数.
1.“票房收入问题”中y=10x,对于x的每一个值,y都有
的值与之对应,所以
是自变量,y是x的函数.当x=1时,函数值y=10,当x=2时,函数值y=20.
2.“行程问题”中s=60t,对于t的每一个值,s都有
的值与之对应,所以
是自变量,
是
的函数.
3.“气温变化问题”,对于时间t的每一个值,气温T都
有
的值与之对应,所以
是自变量,
是
的函数.
归纳:如果有两个变量X和Y,对于x的每一个值,y都有
的值与之对应,称x是
,y是x的
.
唯一
x
唯一
t
s
t
t
T
t
唯一
自变量
函数
唯一
可见,函数是刻画变量之间对应关系的数学模型,许多
问题中变量之间的关系都可以用函数来表示。
3,函数概念的理解:
1).构成函数概念的三个条件:
(1)有一个变化过程;
(2)在这个变化过程中有两个相互依存的变量;
(3)当其中一个变量取定一个数值时,另一个
变量也相应的有唯一确定的一个数值。
2).自变量x有一定的取值范围,在不同的问题中自变量的取值范围不同。
目标2.掌握函数的概念,会判断两个变量的关系是否可看作函数
3)如何理解“对于x的每一个确定的值,y都有唯一确定的值与其对应”这句话?
指明了变量x与y的对应关系可以是:“一对一”“二对一”或“多对一”,如果是“一对多”的情况就不是函数了.
(1)
xy=2;
(3)
x+y=5;
(5)
y=x2-4x+5
(2)
x2+y2=10;
(4)
|y|=x;
(6)
y=
|x|
(1)
指出下列变化关系中,哪些y是x的函数,哪些不是?说出你的理由。
是
否
是
是
否
是
该你显身手了!
(2):下列曲线中,表示y不是x的函数是(
),怎样改动这条曲线,才能使y是x的函数?
A
x
y
O
B
x
y
O
C
x
y
O
D
x
y
O
例1:
一个三角形的底边为5,高h可以任意伸缩,三角形的面积也随之发生了变化.
解:(1)面积s随高h变化的关系式s
=
,
其中常量是
,变量是
,
是自变量,
是
的函数;
(2)当h=3时,面积s=______,
(3)当h=10时,面积s=______;
目标3:精讲例题,运用概念
解:(1)
函数关系式为:
y
=
50-0.1x
(2)
由x≥0及50-0.1x
≥0 得 0
≤
x
≤
500
∴自变量的取值范围是:
0
≤
x
≤
500
(3)当
x
=
200时,函数
y
的值为:y=50-0.1×200=30
因此,当汽车行驶200
km时,油箱中还有油30L
例2:
汽车油箱有汽油50
L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程
x(单位:km)的增加而减少,平均油耗为0.1L/km.
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3)汽车行驶200
km时,油箱中还有多少汽油?
象y=50-0.1x这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法.这种式子叫做函数的解析式.
1.请找出这些函数的常量、变量、自变量和函数:
(1)
y
=3000-300x
(2)
S=570-95t
(3)
y=x
解:(1)常量是3000,-300;变量是x,y;自变量是x;y是x的函数。
(2)常量是570,-95;变量是t,s;自变量是t;s是t的函数。
(3)常量是1;变量是x,y;自变量是x;y是x的函数。
目标4:及时训练,巩固提高
2,购买一些签字笔,单价3元,总价为y元,签字笔为x支,根据题意填表:
(1)y随x变化的关系式y=
,
是自变量,
是
的函数;
(2)当购买8支签字笔时,总价为
元.
3.一个梯形的上底是4,下底是9,写出面积S随高h变化的函数关系式
,常量是
,变量是
,
自变量是
,
是
的函数。
x(支)
1
2
3
…
y(元)
4,填表并回答问题:
(1)对于x的每一个值,y都有唯一的值与之对应吗?答:
。
(2)y是x的函数吗?为什么?
x
1
4
9
16
y=+2x
2和-2
8和-8
18和-18
32和-32
不是
答:不是,因为y的值不是唯一的。
S=x?,S是x的函数,x是自变量;
y=0.1x,y是x的函数,x是自变量;
v=10-0.05t,v是t的函数,t是自变量.
,y是n的函数,n是自变量;
y
=
——
10
n
6
思考:
我市白天乘坐出租车收费标准如下:乘坐里程不超过3公里,一律收费8元;超过3公里时,超过3公里的部分,每公里加收1.8元;设乘坐出租车的里程为x(公里)(x为整数),相对应的收费为y(元).
(1)请分别写出当0<x≤3和x>3时,表示y与x的关系式,并直接写出当x=2和x=6时对应的y值;
(2)当0<x≤3和x>3时,y都是x的函数吗?为什么?
解:(1)当0<x≤3时,y=8;
当x>3时,y=8+1.8(x-3)=1.8x+2.6.
当x=2时,y=8;x=6时,y=1.8×6+2.6=13.4.
(2)当0<x≤3和x>3时,y都是x的函数,因为对于x的每一个确定的值,y都有唯一确定的值与其对应.
19.1.1变量与常量
目标1.
结合具体事例能理解变量与常量的概念,会指出变化中的变量与常量
1.票房收入问题:每张电影票的售价为10元.
(1)若一场售出150张电影票,则该场的票房收入
是
元;
(2)若一场售出205张电影票,则该场的票房收入
是
元;
(3)若设一场售出x张电影票,票房收入为
y元,则
y=
。
小结:票房收入随售出的电影票数变化而变化,即
y随
的变化而变化;
2.行程问题:汽车以60千米/小时的速度匀速行驶,行驶里程为s千米,行驶时间为t小时.请根据题意填表:
小结:行驶路程随
的变化而变化,有关系式s=
,即s随
的变化而变化;
t(时)
1
2
3
…
10
S(千米)
1500
2050
10x
x
60
120
180
600
时间
60t
t
目标1.结合具体事例能理解变量与常量的概念,并会指出变化中的变量与常量
3.温度变化问题:如图一,是北京春季某一天的气温T随时间t变化的图象,看图回答:
(1)这天的8时的气温是
℃,14时的气温是
℃,22时的气温是
℃;
(2)这一天中,最高气温是
℃,最低气温
是
℃;
小结:天气温度随
的变化而变化,即T随
的变化而变化;
4
8
6
10
-2
时间
t
在上面的问题反映了不同事物的变化过程,其中有些量(例如售出票数x,票房收入y;时间t,路程s……)的值按照某种规律
,有些量的值始终
(例如电影票的单价10元……)。
变化
不变
目标1.结合具体事例能理解变量与常量的概念,并会指出变化中的变量与常量
二、问题引申:
常量、变量的概念:
在一个变化过程中:发生变化的量叫做
;不变的量叫做
;
指出前面三个问题中的常量、变量.
(1)“票房收入问题”中y=10x,常量是
,变量是
;
(2)“行程问题”中s=60t,常量是
,变量是
;
(3)“气温变化问题”,
变量是
;
变量
常量
10
x和y
60
t和s
t和T
练习一:
1.某位教师为学生购买数学辅导书,书的单价是4元,则总金额y(元)与学生数n(个)的关系式是
。其中的变量是
。常量是
。
2.计划购买50元的乒乓球,所能购买的总数n(个)与单价
a(元)的关系式为
。其中的变量是
,常量是
。
3.圆的周长公式
,这里的变量是
,常量是
。
4.下列表格是王辉从4岁到10岁的体重情况
这个问题中的变量是
。
年龄(岁)
4
5
6
7
8
9
10
…
体重(千克)
15.4
16.7
18.0
19.6
21.5
23.2
25.2
…
y=4n
n和y
4
n=50/a
a和n
50
r和C
年龄和体重
想一想:
在学习了变量之后,我们会发现两个变量的变化并不是孤立地发生,而是存在一些互相联系,你能说出它是什么吗?
目标2.掌握函数的概念,会判断两个变量的关系是否可看作函数,
以上所举变化过程中,两个变量之间的对应关系都满足:对于一个变量取定一个值时,另一个变量就有唯一确定的值与其对应.
例如:若一场售出150张电影票,则该场的票房收入是
1500
元
若一场售出205张电影票,则该场的票房收入
是
2050
元;
1、函数的概念
目标2.掌握函数的概念,会判断两个变量
的关系是否可看作函数
一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值。
2.自变量、函数、函数值:
指出前面三个问题中的自变量与函数.
1.“票房收入问题”中y=10x,对于x的每一个值,y都有
的值与之对应,所以
是自变量,y是x的函数.当x=1时,函数值y=10,当x=2时,函数值y=20.
2.“行程问题”中s=60t,对于t的每一个值,s都有
的值与之对应,所以
是自变量,
是
的函数.
3.“气温变化问题”,对于时间t的每一个值,气温T都
有
的值与之对应,所以
是自变量,
是
的函数.
归纳:如果有两个变量X和Y,对于x的每一个值,y都有
的值与之对应,称x是
,y是x的
.
唯一
x
唯一
t
s
t
t
T
t
唯一
自变量
函数
唯一
可见,函数是刻画变量之间对应关系的数学模型,许多
问题中变量之间的关系都可以用函数来表示。
3,函数概念的理解:
1).构成函数概念的三个条件:
(1)有一个变化过程;
(2)在这个变化过程中有两个相互依存的变量;
(3)当其中一个变量取定一个数值时,另一个
变量也相应的有唯一确定的一个数值。
2).自变量x有一定的取值范围,在不同的问题中自变量的取值范围不同。
目标2.掌握函数的概念,会判断两个变量的关系是否可看作函数
3)如何理解“对于x的每一个确定的值,y都有唯一确定的值与其对应”这句话?
指明了变量x与y的对应关系可以是:“一对一”“二对一”或“多对一”,如果是“一对多”的情况就不是函数了.
(1)
xy=2;
(3)
x+y=5;
(5)
y=x2-4x+5
(2)
x2+y2=10;
(4)
|y|=x;
(6)
y=
|x|
(1)
指出下列变化关系中,哪些y是x的函数,哪些不是?说出你的理由。
是
否
是
是
否
是
该你显身手了!
(2):下列曲线中,表示y不是x的函数是(
),怎样改动这条曲线,才能使y是x的函数?
A
x
y
O
B
x
y
O
C
x
y
O
D
x
y
O
例1:
一个三角形的底边为5,高h可以任意伸缩,三角形的面积也随之发生了变化.
解:(1)面积s随高h变化的关系式s
=
,
其中常量是
,变量是
,
是自变量,
是
的函数;
(2)当h=3时,面积s=______,
(3)当h=10时,面积s=______;
目标3:精讲例题,运用概念
解:(1)
函数关系式为:
y
=
50-0.1x
(2)
由x≥0及50-0.1x
≥0 得 0
≤
x
≤
500
∴自变量的取值范围是:
0
≤
x
≤
500
(3)当
x
=
200时,函数
y
的值为:y=50-0.1×200=30
因此,当汽车行驶200
km时,油箱中还有油30L
例2:
汽车油箱有汽油50
L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程
x(单位:km)的增加而减少,平均油耗为0.1L/km.
(1)写出表示y与x的函数关系的式子;
(2)指出自变量x的取值范围;
(3)汽车行驶200
km时,油箱中还有多少汽油?
象y=50-0.1x这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法.这种式子叫做函数的解析式.
1.请找出这些函数的常量、变量、自变量和函数:
(1)
y
=3000-300x
(2)
S=570-95t
(3)
y=x
解:(1)常量是3000,-300;变量是x,y;自变量是x;y是x的函数。
(2)常量是570,-95;变量是t,s;自变量是t;s是t的函数。
(3)常量是1;变量是x,y;自变量是x;y是x的函数。
目标4:及时训练,巩固提高
2,购买一些签字笔,单价3元,总价为y元,签字笔为x支,根据题意填表:
(1)y随x变化的关系式y=
,
是自变量,
是
的函数;
(2)当购买8支签字笔时,总价为
元.
3.一个梯形的上底是4,下底是9,写出面积S随高h变化的函数关系式
,常量是
,变量是
,
自变量是
,
是
的函数。
x(支)
1
2
3
…
y(元)
4,填表并回答问题:
(1)对于x的每一个值,y都有唯一的值与之对应吗?答:
。
(2)y是x的函数吗?为什么?
x
1
4
9
16
y=+2x
2和-2
8和-8
18和-18
32和-32
不是
答:不是,因为y的值不是唯一的。
S=x?,S是x的函数,x是自变量;
y=0.1x,y是x的函数,x是自变量;
v=10-0.05t,v是t的函数,t是自变量.
,y是n的函数,n是自变量;
y
=
——
10
n
6
思考:
我市白天乘坐出租车收费标准如下:乘坐里程不超过3公里,一律收费8元;超过3公里时,超过3公里的部分,每公里加收1.8元;设乘坐出租车的里程为x(公里)(x为整数),相对应的收费为y(元).
(1)请分别写出当0<x≤3和x>3时,表示y与x的关系式,并直接写出当x=2和x=6时对应的y值;
(2)当0<x≤3和x>3时,y都是x的函数吗?为什么?
解:(1)当0<x≤3时,y=8;
当x>3时,y=8+1.8(x-3)=1.8x+2.6.
当x=2时,y=8;x=6时,y=1.8×6+2.6=13.4.
(2)当0<x≤3和x>3时,y都是x的函数,因为对于x的每一个确定的值,y都有唯一确定的值与其对应.
