2020-2021学年人教版八年级数学下册:18.1平行四边形的性质(第1课时) 学案
文档属性
| 名称 | 2020-2021学年人教版八年级数学下册:18.1平行四边形的性质(第1课时) 学案 |  | |
| 格式 | zip | ||
| 文件大小 | 107.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 12:03:01 | ||
图片预览

文档简介
18.1平行四边形
师生共用导学稿
学科:数学
教材版本:人教版
学校:
年级:八年级
姓名:
课题:18.1平行四边形的性质
课时:第1课时
〖学习目标〗
1.掌握平行四边形的定义;
2.掌握平行四边形的性质1、
2并会运用性质进行有关的论证和计算.
〖课前回顾〗
1.由__
_条线段首尾顺次连接组成的多边形叫四边形;四边形有
_条边,_
__个角,四边形的内角和等于_____度;
2.如图AB与BC叫_
__边,
AB与CD叫__
_边;
∠A与∠B叫_
__角,∠B与∠D叫_
__角;
〖自主学习〗
学:一、探究新知1.平行四边形的定义
问题1:你能利用手中两张全等的三角形纸板拼出四边形吗?(展示:贴在黑板上)
问题2:观察拼出的这个四边形的对边有怎样的位置关系?
问题3:黑板上展示的图形中,哪些是平行四边形呢?
阅读课本41—42页例1上,完成下面填空:
1.定义:如图,_____________
______的四边形叫做平行四边形.
用几何语言表示为:
∵
∥
,
∥
∴四边形ABCD是平行四边形
2.平行四边形的表示方法:
如右图平行四边形ABCD,
记作____
______
巩固练习:如图是某区部分街道示意图,其中BC∥AD∥EG,AB∥FH∥DC.图中的平行四边形共有_____个.
二、探究新知2.平行四边形的性质
平行四边形除了“两组对边分别平行”外,它的边、角之间还有什么关系?用尺和量角器度量一下.
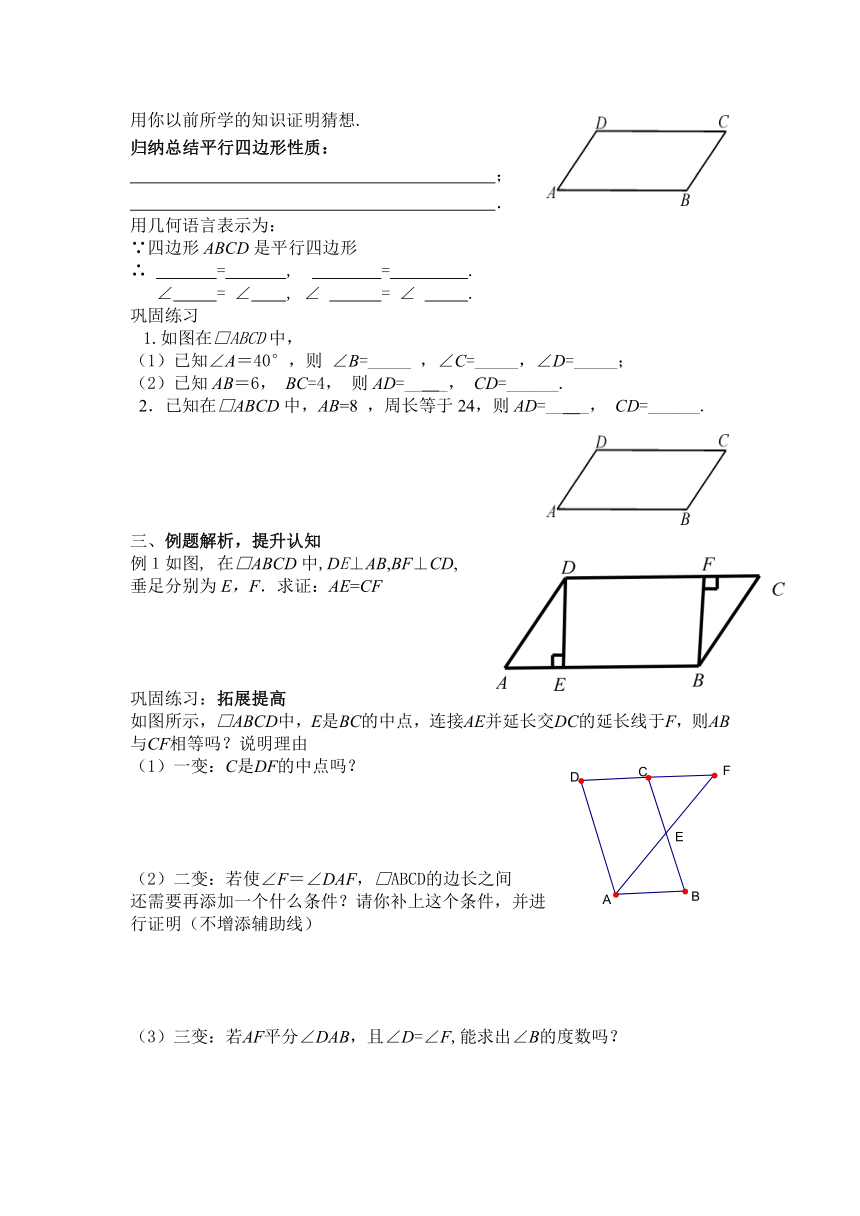
用你以前所学的知识证明猜想.
归纳总结平行四边形性质:
;
.
用几何语言表示为:
∵四边形ABCD是平行四边形
∴
=
,
=
.
∠
=
∠
,
∠
=
∠
.
巩固练习
1.如图在□ABCD中,
(1)已知∠A=40°,则
∠B=_____
,∠C=_____,∠D=_____;
(2)已知AB=6,
BC=4,
则AD=__
_,
CD=______.
2.已知在□ABCD中,AB=8
,周长等于24,则AD=__
_,
CD=______.
三、例题解析,提升认知
例1如图,
在□ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF
巩固练习:拓展提高
如图所示,□ABCD中,E是BC的中点,连接AE并延长交DC的延长线于F,则AB与CF相等吗?说明理由
(1)一变:C是DF的中点吗?
(2)二变:若使∠F=∠DAF,□ABCD的边长之间
还需要再添加一个什么条件?请你补上这个条件,并进行证明(不增添辅助线)
(3)三变:若AF平分∠DAB,且∠D=∠F,能求出∠B的度数吗?
(4)四变:若在□ABCD中,延长DC到F使DC=CF,连接AF交BC于点E,则E是BC的中点吗?
四、探究新知3.平行线之间的距离
1.如图1,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个四边形,线段AD和BC的长度有什么关系?
2.已知,直线a//b,过直线a上任两点A,B分别向直线b作垂线,交直线b于点C,点D,如图,
(1)线段AC,BD所在直线有什么样的位置关系?
(2)比较线段AC,BD的长。
归纳:
_________________________________________________________
注意:
???
(1)两相交直线无距离可言
???
(2)与两点的距离、点到直线的距离的区别与联系
3、你能举出反映“平行线之间的垂直线段处处相等实例吗”?(小组合作)
巩固练习:
1.如图,已知L1//L2,AB//CD,CE⊥L2点E,FG⊥L2于点G,
则下列说法中错误的是(
)
(A)
AB=CD
(B)CE=FG,
(C)A、B两点间的距离就是线段AB的长度
(D)L1与L2间的距离就是线段CD的长度
2.如图,如果直线l1∥l2,那么△ABC的面积和△DBC的面积是相等的.你能说出理由吗?你还能在这两条平行线l1、l2之间画出其他与△ABC面积相等的三角形吗?
展:〖课堂小结〗本节课你有什么收获?
〖自我测试〗
1.在□
ABCD中,已知其周长为40,且边AB比边BC长2,求四边形各边的长.
2.在□ABCD中,∠A比∠B小20°,求∠C、∠D的度数
3.直线m∥m,m上一点A到n的距离为6cm,B为n上任一点,则B到m
的距离为__________cm.
练:课后作业:
1.在□ABCD中,∠A+
∠C=
150°那么∠A=________,∠D=________
2.在□ABCD中,∠A:∠B=
4:5,那么,∠B=________,∠C=_________
3.如图,在□ABCD中,已知AD=8㎝,
AB=6㎝,
DE平分∠ADC交BC边于点E,则BE等于(
)
A.2cm
B.4cm
C.6cm
D.8cm
4.如图,□ABCD的周长为20cm,AE、AF是BC、CD边上的高,且cm,cm,试求平行四边形ABCD的面积。
5.四边形ABCD是平行四边形,已知AD=8,AB=10,BD=6,求BC、CD及此平行四边形的面积.
6.如图,□
ABCD中,、分别为、边
上的点,要使需添加一个条件:
.
并证明.
本课小结:我的收获
新名词:
新观点:
新体验:
新感受:
我将改变我的:
★
课后反思:
(1)
本节课我收了什么?
(2)还有哪些不懂的问题?
m
n
A
B
A
B
C
D
E
A
B
C
E
D
F
师生共用导学稿
学科:数学
教材版本:人教版
学校:
年级:八年级
姓名:
课题:18.1平行四边形的性质
课时:第1课时
〖学习目标〗
1.掌握平行四边形的定义;
2.掌握平行四边形的性质1、
2并会运用性质进行有关的论证和计算.
〖课前回顾〗
1.由__
_条线段首尾顺次连接组成的多边形叫四边形;四边形有
_条边,_
__个角,四边形的内角和等于_____度;
2.如图AB与BC叫_
__边,
AB与CD叫__
_边;
∠A与∠B叫_
__角,∠B与∠D叫_
__角;
〖自主学习〗
学:一、探究新知1.平行四边形的定义
问题1:你能利用手中两张全等的三角形纸板拼出四边形吗?(展示:贴在黑板上)
问题2:观察拼出的这个四边形的对边有怎样的位置关系?
问题3:黑板上展示的图形中,哪些是平行四边形呢?
阅读课本41—42页例1上,完成下面填空:
1.定义:如图,_____________
______的四边形叫做平行四边形.
用几何语言表示为:
∵
∥
,
∥
∴四边形ABCD是平行四边形
2.平行四边形的表示方法:
如右图平行四边形ABCD,
记作____
______
巩固练习:如图是某区部分街道示意图,其中BC∥AD∥EG,AB∥FH∥DC.图中的平行四边形共有_____个.
二、探究新知2.平行四边形的性质
平行四边形除了“两组对边分别平行”外,它的边、角之间还有什么关系?用尺和量角器度量一下.
用你以前所学的知识证明猜想.
归纳总结平行四边形性质:
;
.
用几何语言表示为:
∵四边形ABCD是平行四边形
∴
=
,
=
.
∠
=
∠
,
∠
=
∠
.
巩固练习
1.如图在□ABCD中,
(1)已知∠A=40°,则
∠B=_____
,∠C=_____,∠D=_____;
(2)已知AB=6,
BC=4,
则AD=__
_,
CD=______.
2.已知在□ABCD中,AB=8
,周长等于24,则AD=__
_,
CD=______.
三、例题解析,提升认知
例1如图,
在□ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:AE=CF
巩固练习:拓展提高
如图所示,□ABCD中,E是BC的中点,连接AE并延长交DC的延长线于F,则AB与CF相等吗?说明理由
(1)一变:C是DF的中点吗?
(2)二变:若使∠F=∠DAF,□ABCD的边长之间
还需要再添加一个什么条件?请你补上这个条件,并进行证明(不增添辅助线)
(3)三变:若AF平分∠DAB,且∠D=∠F,能求出∠B的度数吗?
(4)四变:若在□ABCD中,延长DC到F使DC=CF,连接AF交BC于点E,则E是BC的中点吗?
四、探究新知3.平行线之间的距离
1.如图1,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中一张,重合的部分构成了一个四边形,线段AD和BC的长度有什么关系?
2.已知,直线a//b,过直线a上任两点A,B分别向直线b作垂线,交直线b于点C,点D,如图,
(1)线段AC,BD所在直线有什么样的位置关系?
(2)比较线段AC,BD的长。
归纳:
_________________________________________________________
注意:
???
(1)两相交直线无距离可言
???
(2)与两点的距离、点到直线的距离的区别与联系
3、你能举出反映“平行线之间的垂直线段处处相等实例吗”?(小组合作)
巩固练习:
1.如图,已知L1//L2,AB//CD,CE⊥L2点E,FG⊥L2于点G,
则下列说法中错误的是(
)
(A)
AB=CD
(B)CE=FG,
(C)A、B两点间的距离就是线段AB的长度
(D)L1与L2间的距离就是线段CD的长度
2.如图,如果直线l1∥l2,那么△ABC的面积和△DBC的面积是相等的.你能说出理由吗?你还能在这两条平行线l1、l2之间画出其他与△ABC面积相等的三角形吗?
展:〖课堂小结〗本节课你有什么收获?
〖自我测试〗
1.在□
ABCD中,已知其周长为40,且边AB比边BC长2,求四边形各边的长.
2.在□ABCD中,∠A比∠B小20°,求∠C、∠D的度数
3.直线m∥m,m上一点A到n的距离为6cm,B为n上任一点,则B到m
的距离为__________cm.
练:课后作业:
1.在□ABCD中,∠A+
∠C=
150°那么∠A=________,∠D=________
2.在□ABCD中,∠A:∠B=
4:5,那么,∠B=________,∠C=_________
3.如图,在□ABCD中,已知AD=8㎝,
AB=6㎝,
DE平分∠ADC交BC边于点E,则BE等于(
)
A.2cm
B.4cm
C.6cm
D.8cm
4.如图,□ABCD的周长为20cm,AE、AF是BC、CD边上的高,且cm,cm,试求平行四边形ABCD的面积。
5.四边形ABCD是平行四边形,已知AD=8,AB=10,BD=6,求BC、CD及此平行四边形的面积.
6.如图,□
ABCD中,、分别为、边
上的点,要使需添加一个条件:
.
并证明.
本课小结:我的收获
新名词:
新观点:
新体验:
新感受:
我将改变我的:
★
课后反思:
(1)
本节课我收了什么?
(2)还有哪些不懂的问题?
m
n
A
B
A
B
C
D
E
A
B
C
E
D
F
