_ 2020-2021学年北师大版八年级数学下册第1章三角形的证明课后提升作业题(word版含答案)
文档属性
| 名称 | _ 2020-2021学年北师大版八年级数学下册第1章三角形的证明课后提升作业题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 275.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-02 22:49:48 | ||
图片预览


文档简介
2020-2021年度北师大版八年级数学下册第1章三角形的证明课后提升作业题(附答案)
1.A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,为拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB中点
B.BC中点
C.AC中点
D.∠C的平分线与AB的交点
2.如图,在△ABC中,BC=10cm,AB的垂直平分线交AB于点D,交边AC于点E,若△BCE的周长等于22cm,则AC的长度等于( )
A.10cm
B.12cm
C.22cm
D.32cm
3.能把三角形分割成面积相等两部分的一定是( )
A.三角形的中线
B.三角形的角平分线
C.三角形的高线
D.三角形一边上的垂直平分线
4.如图,若记北京为A地,莫斯科为B地,雅典为C地,若想建立一个货物中转仓,使其到A、B、C三地的距离相等,则中转仓的位置应选在( )
A.三边垂直平分线的交点
B.三边中线的交点
C.三条角平分线的交点
D.三边上高的交点
5.如图,直线l是线段AB的垂直平分线,点C在直线l外,且与A点在直线l的同一侧,点P是直线l上的任意点,连接AP,BC,CP,则BC与AP+PC的大小关系是( )
A.>
B.<
C.≥
D.≤
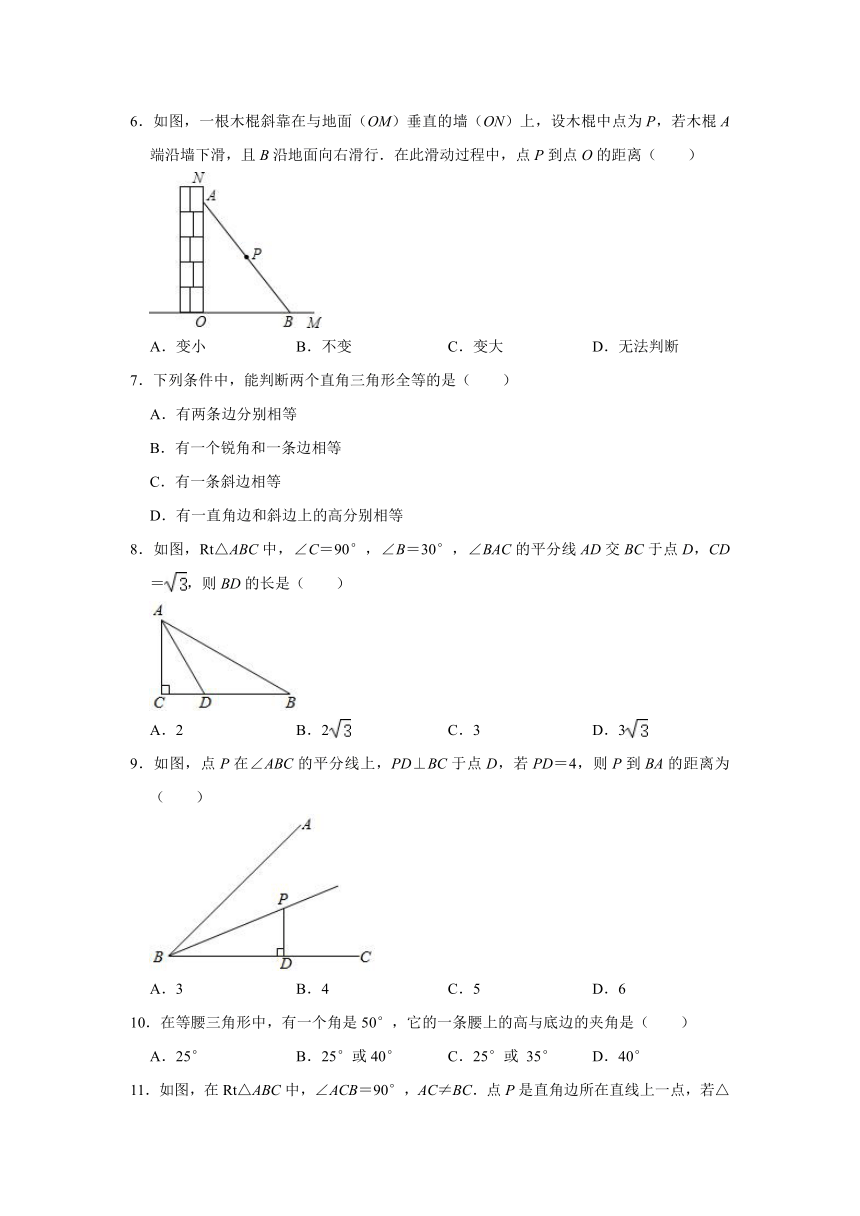
6.如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离( )
A.变小
B.不变
C.变大
D.无法判断
7.下列条件中,能判断两个直角三角形全等的是( )
A.有两条边分别相等
B.有一个锐角和一条边相等
C.有一条斜边相等
D.有一直角边和斜边上的高分别相等
8.如图,Rt△ABC中,∠C=90°,∠B=30°,∠BAC的平分线AD交BC于点D,CD=,则BD的长是( )
A.2
B.2
C.3
D.3
9.如图,点P在∠ABC的平分线上,PD⊥BC于点D,若PD=4,则P到BA的距离为( )
A.3
B.4
C.5
D.6
10.在等腰三角形中,有一个角是50°,它的一条腰上的高与底边的夹角是( )
A.25°
B.25°或40°
C.25°或
35°
D.40°
11.如图,在Rt△ABC中,∠ACB=90°,AC≠BC.点P是直角边所在直线上一点,若△PAB为等腰三角形,则符合条件的点P的个数最多为( )
A.3个
B.6个
C.7个
D.8个
12.下列说法错误的是( )
A.等腰三角形的两个底角相等
B.等腰三角形的高、中线、角平分线互相重合
C.三角形两边的垂直平分线的交点到三个顶点距离相等
D.等腰三角形顶角的外角是其底角的2倍
13.如图在第一个△A1BC中,∠B=40°,A1B=BC,在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第二个△A1A2D,再在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E.……如此类推,可得到第n个等腰三角形.则第n个等腰三角形中,以An为顶点的内角的度数为( )
A.
B.
C.
D.
14.如图,点P在∠AOB的平分线上,PC⊥OA于点C,∠AOB=30°,点D在边OB上,且OD=DP=2.则线段PC的长度为( )
A.3
B.2
C.1
D.
15.若实数m、n满足等式|m﹣2|+=0,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是( )
A.12
B.10
C.8
D.6
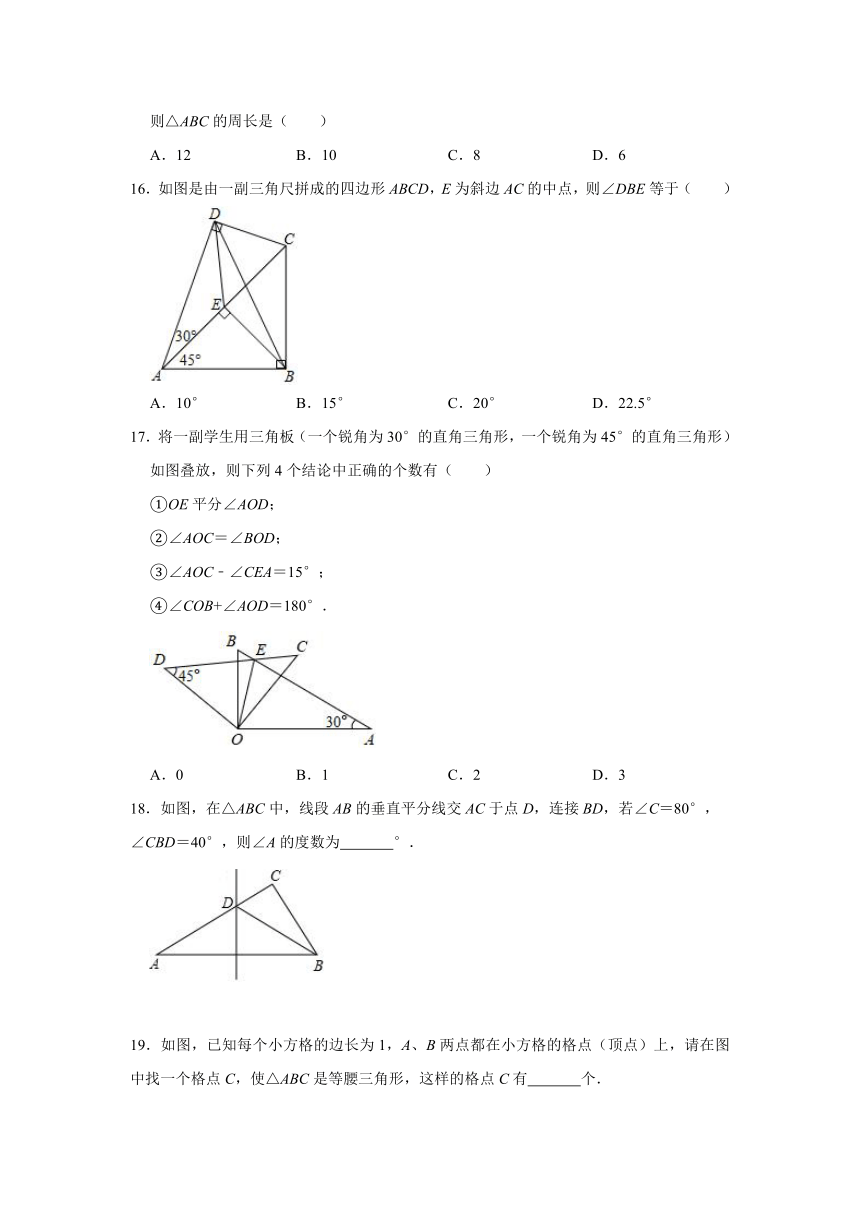
16.如图是由一副三角尺拼成的四边形ABCD,E为斜边AC的中点,则∠DBE等于( )
A.10°
B.15°
C.20°
D.22.5°
17.将一副学生用三角板(一个锐角为30°的直角三角形,一个锐角为45°的直角三角形)如图叠放,则下列4个结论中正确的个数有( )
①OE平分∠AOD;
②∠AOC=∠BOD;
③∠AOC﹣∠CEA=15°;
④∠COB+∠AOD=180°.
A.0
B.1
C.2
D.3
18.如图,在△ABC中,线段AB的垂直平分线交AC于点D,连接BD,若∠C=80°,
∠CBD=40°,则∠A的度数为
°.
19.如图,已知每个小方格的边长为1,A、B两点都在小方格的格点(顶点)上,请在图中找一个格点C,使△ABC是等腰三角形,这样的格点C有
个.
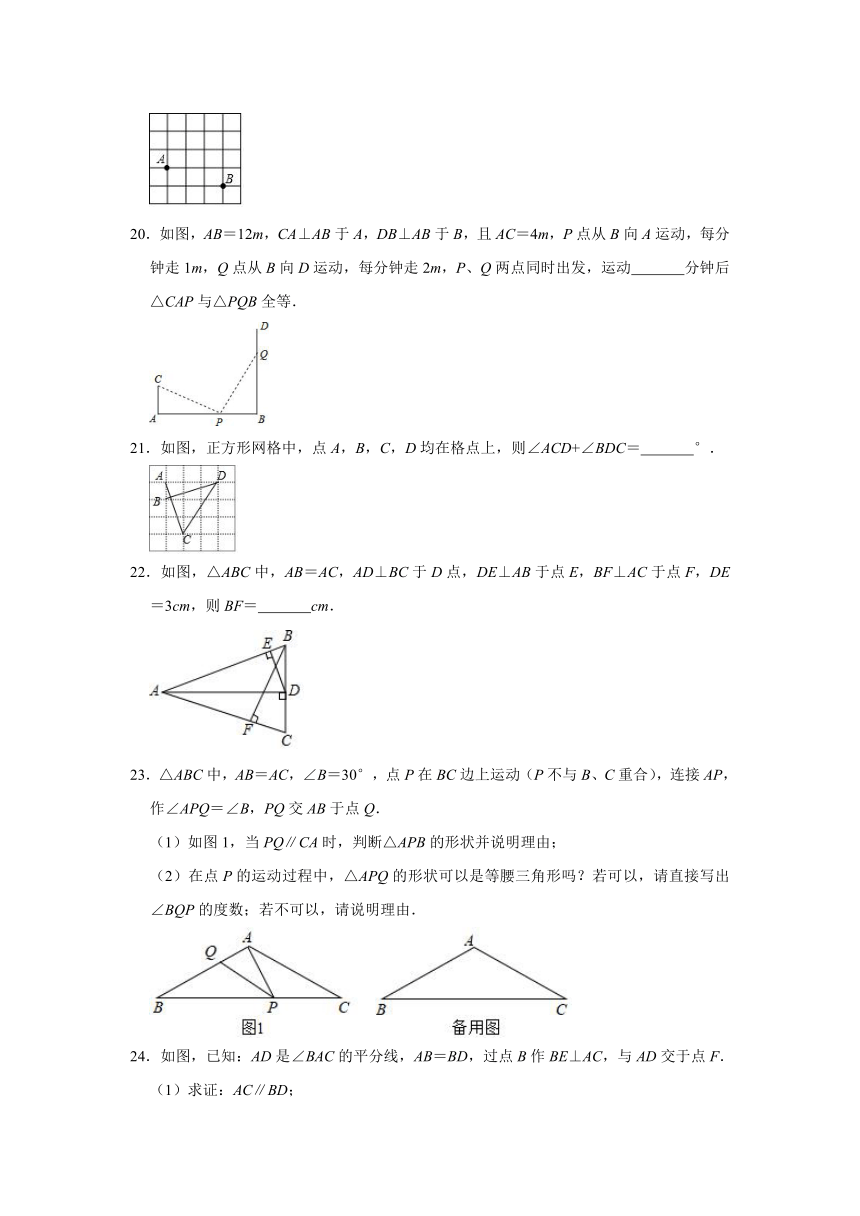
20.如图,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动
分钟后△CAP与△PQB全等.
21.如图,正方形网格中,点A,B,C,D均在格点上,则∠ACD+∠BDC=
°.
22.如图,△ABC中,AB=AC,AD⊥BC于D点,DE⊥AB于点E,BF⊥AC于点F,DE=3cm,则BF=
cm.
23.△ABC中,AB=AC,∠B=30°,点P在BC边上运动(P不与B、C重合),连接AP,作∠APQ=∠B,PQ交AB于点Q.
(1)如图1,当PQ∥CA时,判断△APB的形状并说明理由;
(2)在点P的运动过程中,△APQ的形状可以是等腰三角形吗?若可以,请直接写出∠BQP的度数;若不可以,请说明理由.
24.如图,已知:AD是∠BAC的平分线,AB=BD,过点B作BE⊥AC,与AD交于点F.
(1)求证:AC∥BD;
(2)若AE=2,AB=3,BF=,求△ABF中AB边上的高.
25.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求证:CE=CF;
(2)若CD=2,求DF的长.
26.如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠BAD=
°;点D从B向C运动时,∠BDA逐渐变
(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.
27.如图,已知Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠BAC的平分线分别交BC,CD于点E、F.
(1)试说明△CEF是等腰三角形;
(2)若点E恰好在线段AB的垂直平分线上,猜想:线段AC与线段AB的数量关系,并说明理由;
(3)在(2)的条件下,若AC=2.5,求△ABE的面积.
28.如图,△ABC中AB=AC,BD和CD分别平分△ABC的内角∠CBA和外角∠ECA,BD交AC于F,连接AD.
(1)求证:AD平分∠GAC;
(2)求证:AD∥BC.
29.如图所示,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC边上的中点,CE⊥AD于点E,BF∥AC交CE的延长线于点F,求证:AB垂直平分DF.
参考答案
1.解:∵AB2=10002=1000000,BC2=6002=360000,AC2=8002640000,
∴AB2=BC2+AC2,
∴△ABC为以AB为斜边的直角三角形,
当点P在AB的中点时,CP=AB=PA=PB,
故选:A.
2.解:∵DE是线段AB的垂直平分线,
∴EA=EB,
∵△BCE的周长等于22cm,
∴BC+CE+BE=22(cm),
∴BC+CE+EA=BC+AC=22(cm),
∵BC=10cm,
∴AC=12(cm),
故选:B.
3.解:能把三角形分割成面积相等两部分的一定是三角形的中线,
故选:A.
4.解:∵中转仓到A、B两地的距离相等,
∴中转仓的位置应选在边AB的垂直平分线上,
同理,中转仓的位置应选在边AC、BC的垂直平分线上,
∵中转仓到A、B、C三地的距离相等,
∴中转仓的位置应选在三边垂直平分线的交点上,
故选:A.
5.解:连接BP,
∵直线l是线段AB的垂直平分线,
∴AP=BP,
∴AP+PC=BP+PC,
当点P在BC与l的交点处时,AP+PC=CB,
当点P不在BC与l的交点处时,AP+PC=BP+PC>BC,
∴BC≤AP+PC,
故选:D.
6.解:在木棍滑动的过程中,点P到点O的距离不发生变化,
理由是:连接OP,
∵∠AOB=90°,P为AB中点,AB=2a,
∴OP=AB=a,
即在木棍滑动的过程中,点P到点O的距离不发生变化,永远是a;
故选:B.
7.解:A、两边分别相等,但是不一定是对应边,不能判定两直角三角形全等,故此选项不符合题意;
B、一条边和一锐角对应相等,不能判定两直角三角形全等,故此选项不符合题意;
C、有一条斜边相等,两直角边不一定对应相等,不能判定两直角三角形全等,故此选项不符合题意;
D、有一条直角边和斜边上的高对应相等的两个直角三角形全等,故此选项符合题意;
故选:D.
8.解:∵∠C=90°,∠B=30°,
∴∠CAB=60°,
∵∠BAC的平分线AD交BC于点D,
∴∠CAD=∠BAD=CAB=30°,
∴∠DAB=∠B,
∴BD=AD,
∵CD=,
∴BD=AD=2CD=2,
故选:B.
9.解:∵BP是∠ABC的平分线,PD⊥BC于点D,
∴点P到边AB的距离等于PD=4.
故选:B.
10.解:当50°为底角时,
∵∠B=∠ACB=50°,
∴∠BCD=90°﹣50°=40°;
当50°为顶角时,
∵∠A=50°,
∴∠B=∠ACB=65°,
∴∠BCD=90°﹣65°=25°.
故选:B.
11.解:①
以B为圆心,以BA为半径作圆,此圆与直线BC交于两点,与直线AC交于一点(A除外),此时BP=AB;
②
以A为圆心,以AB为半径作圆,此圆与直线AC交于两点,与直线AB交于一点(B除外),此时AP=AB;
③
作线段AB的垂直平分线,交直线AC于一点,交直线BC于一点,此时AP=BP;
(1+2)+(1+2)+1+1=8,
故选:D.
12.解:A.等腰三角形的两底角相等,故本选项不符合题意;
B.等腰三角形的两个底角的高、角平分线和中线不一定互相重合,故本选项符合题意;
C.
过O作OM⊥AB于M,OQ⊥AC于Q,ON⊥BC于N,
∵O是∠ABC和∠ACB的角平分线的交点,
∴OM=ON,ON=OQ,
∴OM=ON=OQ,
即三角形的两边的垂直平分线的交点到三个顶点的距离相等,故本选项不符合题意;
D.
∵AB=AC,
∴∠B=∠C,
∵∠EAC=∠B+∠C,
∴∠EAC=2∠B,
即等腰三角形顶角的外角是其底角的2倍,故本选项不符合题意;
故选:B.
13.解:在△CBA1中,∠B=40°,A1B=CB,
∴∠BA1C==70°,
∵A1A2=A1D,∠BA1C是△A1A2D的外角,
∴∠DA2A1=∠BA1C=×70°,
同理可得∠EA3A2=()2×70°,∠FA4A3=()3×70°,
∴第n个三角形中以An为顶点的内角度数是()n﹣1×70°.
故选:C.
14.解:过P作PE⊥OB于E,
∵点P在∠AOB的平分线上,PC⊥OA,
∴PC=PE,∠AOP=∠BOP,
∵OD=DP,
∴∠BOP=∠DPO,
∴∠AOP=∠DPO,
∴PD∥OA,
∴∠PDE=∠AOB,
∵∠AOB=30°,
∴∠PDE=30°,
∵∠PEO=90°,DP=2,
∴PE=DP=1,
∴PC=1,
故选:C.
15.解:∵|m﹣2|+=0,
∴m﹣2=0,n﹣4=0,
解得m=2,n=4,
当m=2作腰时,三边为2,2,4,不符合三边关系定理;
当n=4作腰时,三边为2,4,4,符合三边关系定理,周长为:2+4+4=10.
故选:B.
16.解:在直角△ACD中,∠ADC=90°,∠DAC=30°,则∠ACD=60°.
又∵E为斜边AC的中点,
∴DE=EC=AC.
∴∠DEC=∠ECD=60°.
∵∠BED=90°,
∴∠BED=150°.
在直角△ABC中,E为斜边AC的中点,则BE=AC.
∴DE=BE,
∴∠DBE=EDB=×(180°﹣150°)=15°.
故选:B.
17.解:∵∠DOC=∠AOB=90°,
∴∠DOC﹣∠BOC=∠AOB﹣∠COB,
即∠AOC=∠BOD,故②正确;
∵∠AOB=∠COD=90°,
∴∠COB+∠AOD=∠AOB+∠COD=180°,故④正确;
如图,AB与OC交于点P,
∵∠CPE=∠APO,∠C=45°,∠A=30°,∠CEA+∠CPE+∠C=∠AOC+∠APO+∠A=180°,
∴∠AOC﹣∠CEA=15°.故③正确;
没有条件能证明OE平分∠AOD,故①错误.
故选:D.
18.解:∵∠C=80°,∠CBD=40°,
∴∠CDB=180°﹣∠C﹣∠CBD=60°,
∵线段AB的垂直平分线交AC于点D,
∴DA=DB,
∴∠A=∠DBA=∠CDB=30°,
故答案为:30.
19.解:如图,△ABC是等腰三角形,这样的格点C有8个.
故答案为8.
20.解:∵CA⊥AB于A,DB⊥AB于B,
∴∠A=∠B=90°,
设运动x分钟后△CAP与△PQB全等;
则BP=xm,BQ=2xm,则AP=(12﹣x)m,
分两种情况:
①若BP=AC,则x=4,
AP=12﹣4=8,BQ=8,AP=BQ,
∴△CAP≌△PBQ;
②若BP=AP,则12﹣x=x,
解得:x=6,BQ=12≠AC,
此时△CAP与△PQB不全等;
综上所述:运动4分钟后△CAP与△PQB全等;
故答案为:4.
21.解:在Rt△AEC和Rt△DAB中
∴Rt△AEC≌Rt△DAB(HL),
∴∠ACE=∠ABD,
∵∠EAC+∠ACE=90°,
∴∠EAC+∠ABD=90°,
∴∠AFB=90°,即∠CFD=90°,
∴∠ACD+∠BDC=90°,
故答案为90.
22.解:在Rt△ADB与Rt△ADC中,
,
∴Rt△ADB≌Rt△ADC,
∴S△ABC=2S△ABD=2×AB?DE=AB?DE=3AB,
∵S△ABC=AC?BF,
∴AC?BF=3AB,
∵AC=AB,
∴BF=3,
∴BF=6.
故答案为6.
23.解:(1)△APB是直角三角形,
理由如下:∵AB=AC,∠B=30°,
∴∠C=30°=∠B=∠APQ,
∵PQ∥AC,
∴∠BPQ=∠C,
∴∠APB=60°,
∴∠BAP=90°,
∴△APB是直角三角形;
(2)当AQ=QP时,
∴∠QAP=∠APQ=30°,
∴∠BQP=∠QAP+∠APQ=60°,
当AP=PQ时,则∠AQP=∠PAQ=75°,
∴∠BQP=105°,
当AQ=AP时,则∠AQP=∠APQ=30°,
∵P不与B、C重合,
∴不存在,
综上所述:∠BQP=105°或60°.
24.(1)证明:∵AD是∠BAC的平分线,
∴∠CAD=∠BAD,
∵AB=BD,
∴∠BDA=∠BAD,
∴∠CAD=∠BDA,
∴AC∥BD;
(2)解:作FG⊥AB于G,
在Rt△ABE中,AE=2,AB=3,
∴BE===,
∴FE=BE﹣BF=﹣=,
∵AD是∠BAC的平分线,BE⊥AC,作FG⊥AB,
∴FG=FE=,即△ABF中AB边上的高为.
25.证明:(1)∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°.
∵DE∥AB,
∴∠B=EDC=60°,∠A=∠CED=60°,
∴∠EDC=∠ECD=∠DEC=60°,
∵EF⊥ED,
∴∠DEF=90°,
∴∠F=30°
∵∠F+∠FEC=∠ECD=60°,
∴∠F=∠FEC=30°,
∴CE=CF.
(2)由(1)可知∠EDC=∠ECD=∠DEC=60°,
∴CE=DC=2.
又∵CE=CF,
∴CF=2.
∴DF=DC+CF=2+2=4.
26.解:(1)∠BAD=180°﹣∠ABD﹣∠BDA=180°﹣40°﹣115°=25°;
从图中可以得知,点D从B向C运动时,∠BDA逐渐变小;
故答案为:25°;小.
(2∵∠EDC+∠EDA=∠DAB+∠B,∠B=∠EDA=40°,
∴∠EDC=∠DAB.,
∵∠B=∠C,
∴当DC=AB=2时,△ABD≌△DCE,
(3)∵AB=AC,
∴∠B=∠C=40°,
①当AD=AE时,∠ADE=∠AED=40°,
∵∠AED>∠C,
∴此时不符合;
②当DA=DE时,即∠DAE=∠DEA=(180°﹣40°)=70°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=100°﹣70°=30°;
∴∠BDA=180°﹣30°﹣40°=110°;
③当EA=ED时,∠ADE=∠DAE=40°,
∴∠BAD=100°﹣40°=60°,
∴∠BDA=180°﹣60°﹣40°=80°;
∴当∠ADB=110°或80°时,△ADE是等腰三角形.
27.解:(1)∵CD⊥AB,
∴∠CDB=90°,
∴∠B+∠BCD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∴∠ACD=∠B,
∵AE平分∠BAC,
∴∠CAE=∠BAE,
∴∠ACD+∠CAE=∠B+∠BAE,
即∠CFE=∠CEF,
∴CF=CE,
即△CEF是等腰三角形;
(2)AB=2AC,
理由是:∵E在线段AB的垂直平分线上,
∴AE=BE,
∴∠B=∠BAE,
∵∠CAE=∠BAE,∠ACB=90°,
∴3∠B=90°,
∴∠B=30°,
∴AB=2AC;
(3)方法一、过E作EM⊥AB于M,
∵AC=2.5,∠ACB=90°,∠B=∠CAE=30°,
∴AE=2CE,
设CE=2,则AE=2x,
由勾股定理得:AC2+CE2=AE2,
即2.52+x2=(2x)2,
解得:x=,
即CE=,
∵AE平分∠CAB,∠ACB=90°,EM⊥AB,
∴EM=CE=,
∴△ABE的面积S==5×=;
方法二、由勾股定理得:BC=2.5,
∵CE=,
∴BE=BC﹣CE=,
∴△ABE的面积S==××2.5=.
28.(1)证明:过点D作DN⊥BA,DK⊥AC,DM⊥BC,垂足分别为点N、K、M.
∵BD、CD分别平分∠EBA、∠ECA,DN⊥BA,DK⊥AC,DM⊥BC,
∴DM=DN=DK,
∴AD平分∠GAC,∠ABD=∠DBC,
∴∠GAD=∠DAC,
∴AD平分∠GAC.
(2)证明:∵∠GAC=∠ABC+∠ACB,∠GAD=∠DAC,
又∵AB=AC,
∴∠ABC=∠ACB,
∴∠GAD=∠ABC,
∴AD∥BC.
29.证明:连接DF,
∵∠BCE+∠ACE=90°,∠ACE+∠CAE=90°,
∴∠BCE=∠CAE.
∵AC⊥BC,BF∥AC.
∴BF⊥BC.
∴∠ACD=∠CBF=90°,
∵AC=CB,
∴△ACD≌△CBF.∴CD=BF.
∵CD=BD=BC,∴BF=BD.
∴△BFD为等腰直角三角形.
∵∠ACB=90°,CA=CB,
∴∠ABC=45°.
∵∠FBD=90°,
∴∠ABF=45°.
∴∠ABC=∠ABF,即BA是∠FBD的平分线.
∴BA是FD边上的高线,BA又是边FD的中线,
即AB垂直平分DF.
1.A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,为拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB中点
B.BC中点
C.AC中点
D.∠C的平分线与AB的交点
2.如图,在△ABC中,BC=10cm,AB的垂直平分线交AB于点D,交边AC于点E,若△BCE的周长等于22cm,则AC的长度等于( )
A.10cm
B.12cm
C.22cm
D.32cm
3.能把三角形分割成面积相等两部分的一定是( )
A.三角形的中线
B.三角形的角平分线
C.三角形的高线
D.三角形一边上的垂直平分线
4.如图,若记北京为A地,莫斯科为B地,雅典为C地,若想建立一个货物中转仓,使其到A、B、C三地的距离相等,则中转仓的位置应选在( )
A.三边垂直平分线的交点
B.三边中线的交点
C.三条角平分线的交点
D.三边上高的交点
5.如图,直线l是线段AB的垂直平分线,点C在直线l外,且与A点在直线l的同一侧,点P是直线l上的任意点,连接AP,BC,CP,则BC与AP+PC的大小关系是( )
A.>
B.<
C.≥
D.≤
6.如图,一根木棍斜靠在与地面(OM)垂直的墙(ON)上,设木棍中点为P,若木棍A端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离( )
A.变小
B.不变
C.变大
D.无法判断
7.下列条件中,能判断两个直角三角形全等的是( )
A.有两条边分别相等
B.有一个锐角和一条边相等
C.有一条斜边相等
D.有一直角边和斜边上的高分别相等
8.如图,Rt△ABC中,∠C=90°,∠B=30°,∠BAC的平分线AD交BC于点D,CD=,则BD的长是( )
A.2
B.2
C.3
D.3
9.如图,点P在∠ABC的平分线上,PD⊥BC于点D,若PD=4,则P到BA的距离为( )
A.3
B.4
C.5
D.6
10.在等腰三角形中,有一个角是50°,它的一条腰上的高与底边的夹角是( )
A.25°
B.25°或40°
C.25°或
35°
D.40°
11.如图,在Rt△ABC中,∠ACB=90°,AC≠BC.点P是直角边所在直线上一点,若△PAB为等腰三角形,则符合条件的点P的个数最多为( )
A.3个
B.6个
C.7个
D.8个
12.下列说法错误的是( )
A.等腰三角形的两个底角相等
B.等腰三角形的高、中线、角平分线互相重合
C.三角形两边的垂直平分线的交点到三个顶点距离相等
D.等腰三角形顶角的外角是其底角的2倍
13.如图在第一个△A1BC中,∠B=40°,A1B=BC,在边A1B上任取一点D,延长CA1到A2,使A1A2=A1D,得到第二个△A1A2D,再在边A2D上任取一点E,延长A1A2到A3,使A2A3=A2E,得到第3个△A2A3E.……如此类推,可得到第n个等腰三角形.则第n个等腰三角形中,以An为顶点的内角的度数为( )
A.
B.
C.
D.
14.如图,点P在∠AOB的平分线上,PC⊥OA于点C,∠AOB=30°,点D在边OB上,且OD=DP=2.则线段PC的长度为( )
A.3
B.2
C.1
D.
15.若实数m、n满足等式|m﹣2|+=0,且m、n恰好是等腰△ABC的两条边的边长,则△ABC的周长是( )
A.12
B.10
C.8
D.6
16.如图是由一副三角尺拼成的四边形ABCD,E为斜边AC的中点,则∠DBE等于( )
A.10°
B.15°
C.20°
D.22.5°
17.将一副学生用三角板(一个锐角为30°的直角三角形,一个锐角为45°的直角三角形)如图叠放,则下列4个结论中正确的个数有( )
①OE平分∠AOD;
②∠AOC=∠BOD;
③∠AOC﹣∠CEA=15°;
④∠COB+∠AOD=180°.
A.0
B.1
C.2
D.3
18.如图,在△ABC中,线段AB的垂直平分线交AC于点D,连接BD,若∠C=80°,
∠CBD=40°,则∠A的度数为
°.
19.如图,已知每个小方格的边长为1,A、B两点都在小方格的格点(顶点)上,请在图中找一个格点C,使△ABC是等腰三角形,这样的格点C有
个.
20.如图,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动
分钟后△CAP与△PQB全等.
21.如图,正方形网格中,点A,B,C,D均在格点上,则∠ACD+∠BDC=
°.
22.如图,△ABC中,AB=AC,AD⊥BC于D点,DE⊥AB于点E,BF⊥AC于点F,DE=3cm,则BF=
cm.
23.△ABC中,AB=AC,∠B=30°,点P在BC边上运动(P不与B、C重合),连接AP,作∠APQ=∠B,PQ交AB于点Q.
(1)如图1,当PQ∥CA时,判断△APB的形状并说明理由;
(2)在点P的运动过程中,△APQ的形状可以是等腰三角形吗?若可以,请直接写出∠BQP的度数;若不可以,请说明理由.
24.如图,已知:AD是∠BAC的平分线,AB=BD,过点B作BE⊥AC,与AD交于点F.
(1)求证:AC∥BD;
(2)若AE=2,AB=3,BF=,求△ABF中AB边上的高.
25.如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求证:CE=CF;
(2)若CD=2,求DF的长.
26.如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠BAD=
°;点D从B向C运动时,∠BDA逐渐变
(填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状也在改变,判断当∠BDA等于多少度时,△ADE是等腰三角形.
27.如图,已知Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠BAC的平分线分别交BC,CD于点E、F.
(1)试说明△CEF是等腰三角形;
(2)若点E恰好在线段AB的垂直平分线上,猜想:线段AC与线段AB的数量关系,并说明理由;
(3)在(2)的条件下,若AC=2.5,求△ABE的面积.
28.如图,△ABC中AB=AC,BD和CD分别平分△ABC的内角∠CBA和外角∠ECA,BD交AC于F,连接AD.
(1)求证:AD平分∠GAC;
(2)求证:AD∥BC.
29.如图所示,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC边上的中点,CE⊥AD于点E,BF∥AC交CE的延长线于点F,求证:AB垂直平分DF.
参考答案
1.解:∵AB2=10002=1000000,BC2=6002=360000,AC2=8002640000,
∴AB2=BC2+AC2,
∴△ABC为以AB为斜边的直角三角形,
当点P在AB的中点时,CP=AB=PA=PB,
故选:A.
2.解:∵DE是线段AB的垂直平分线,
∴EA=EB,
∵△BCE的周长等于22cm,
∴BC+CE+BE=22(cm),
∴BC+CE+EA=BC+AC=22(cm),
∵BC=10cm,
∴AC=12(cm),
故选:B.
3.解:能把三角形分割成面积相等两部分的一定是三角形的中线,
故选:A.
4.解:∵中转仓到A、B两地的距离相等,
∴中转仓的位置应选在边AB的垂直平分线上,
同理,中转仓的位置应选在边AC、BC的垂直平分线上,
∵中转仓到A、B、C三地的距离相等,
∴中转仓的位置应选在三边垂直平分线的交点上,
故选:A.
5.解:连接BP,
∵直线l是线段AB的垂直平分线,
∴AP=BP,
∴AP+PC=BP+PC,
当点P在BC与l的交点处时,AP+PC=CB,
当点P不在BC与l的交点处时,AP+PC=BP+PC>BC,
∴BC≤AP+PC,
故选:D.
6.解:在木棍滑动的过程中,点P到点O的距离不发生变化,
理由是:连接OP,
∵∠AOB=90°,P为AB中点,AB=2a,
∴OP=AB=a,
即在木棍滑动的过程中,点P到点O的距离不发生变化,永远是a;
故选:B.
7.解:A、两边分别相等,但是不一定是对应边,不能判定两直角三角形全等,故此选项不符合题意;
B、一条边和一锐角对应相等,不能判定两直角三角形全等,故此选项不符合题意;
C、有一条斜边相等,两直角边不一定对应相等,不能判定两直角三角形全等,故此选项不符合题意;
D、有一条直角边和斜边上的高对应相等的两个直角三角形全等,故此选项符合题意;
故选:D.
8.解:∵∠C=90°,∠B=30°,
∴∠CAB=60°,
∵∠BAC的平分线AD交BC于点D,
∴∠CAD=∠BAD=CAB=30°,
∴∠DAB=∠B,
∴BD=AD,
∵CD=,
∴BD=AD=2CD=2,
故选:B.
9.解:∵BP是∠ABC的平分线,PD⊥BC于点D,
∴点P到边AB的距离等于PD=4.
故选:B.
10.解:当50°为底角时,
∵∠B=∠ACB=50°,
∴∠BCD=90°﹣50°=40°;
当50°为顶角时,
∵∠A=50°,
∴∠B=∠ACB=65°,
∴∠BCD=90°﹣65°=25°.
故选:B.
11.解:①
以B为圆心,以BA为半径作圆,此圆与直线BC交于两点,与直线AC交于一点(A除外),此时BP=AB;
②
以A为圆心,以AB为半径作圆,此圆与直线AC交于两点,与直线AB交于一点(B除外),此时AP=AB;
③
作线段AB的垂直平分线,交直线AC于一点,交直线BC于一点,此时AP=BP;
(1+2)+(1+2)+1+1=8,
故选:D.
12.解:A.等腰三角形的两底角相等,故本选项不符合题意;
B.等腰三角形的两个底角的高、角平分线和中线不一定互相重合,故本选项符合题意;
C.
过O作OM⊥AB于M,OQ⊥AC于Q,ON⊥BC于N,
∵O是∠ABC和∠ACB的角平分线的交点,
∴OM=ON,ON=OQ,
∴OM=ON=OQ,
即三角形的两边的垂直平分线的交点到三个顶点的距离相等,故本选项不符合题意;
D.
∵AB=AC,
∴∠B=∠C,
∵∠EAC=∠B+∠C,
∴∠EAC=2∠B,
即等腰三角形顶角的外角是其底角的2倍,故本选项不符合题意;
故选:B.
13.解:在△CBA1中,∠B=40°,A1B=CB,
∴∠BA1C==70°,
∵A1A2=A1D,∠BA1C是△A1A2D的外角,
∴∠DA2A1=∠BA1C=×70°,
同理可得∠EA3A2=()2×70°,∠FA4A3=()3×70°,
∴第n个三角形中以An为顶点的内角度数是()n﹣1×70°.
故选:C.
14.解:过P作PE⊥OB于E,
∵点P在∠AOB的平分线上,PC⊥OA,
∴PC=PE,∠AOP=∠BOP,
∵OD=DP,
∴∠BOP=∠DPO,
∴∠AOP=∠DPO,
∴PD∥OA,
∴∠PDE=∠AOB,
∵∠AOB=30°,
∴∠PDE=30°,
∵∠PEO=90°,DP=2,
∴PE=DP=1,
∴PC=1,
故选:C.
15.解:∵|m﹣2|+=0,
∴m﹣2=0,n﹣4=0,
解得m=2,n=4,
当m=2作腰时,三边为2,2,4,不符合三边关系定理;
当n=4作腰时,三边为2,4,4,符合三边关系定理,周长为:2+4+4=10.
故选:B.
16.解:在直角△ACD中,∠ADC=90°,∠DAC=30°,则∠ACD=60°.
又∵E为斜边AC的中点,
∴DE=EC=AC.
∴∠DEC=∠ECD=60°.
∵∠BED=90°,
∴∠BED=150°.
在直角△ABC中,E为斜边AC的中点,则BE=AC.
∴DE=BE,
∴∠DBE=EDB=×(180°﹣150°)=15°.
故选:B.
17.解:∵∠DOC=∠AOB=90°,
∴∠DOC﹣∠BOC=∠AOB﹣∠COB,
即∠AOC=∠BOD,故②正确;
∵∠AOB=∠COD=90°,
∴∠COB+∠AOD=∠AOB+∠COD=180°,故④正确;
如图,AB与OC交于点P,
∵∠CPE=∠APO,∠C=45°,∠A=30°,∠CEA+∠CPE+∠C=∠AOC+∠APO+∠A=180°,
∴∠AOC﹣∠CEA=15°.故③正确;
没有条件能证明OE平分∠AOD,故①错误.
故选:D.
18.解:∵∠C=80°,∠CBD=40°,
∴∠CDB=180°﹣∠C﹣∠CBD=60°,
∵线段AB的垂直平分线交AC于点D,
∴DA=DB,
∴∠A=∠DBA=∠CDB=30°,
故答案为:30.
19.解:如图,△ABC是等腰三角形,这样的格点C有8个.
故答案为8.
20.解:∵CA⊥AB于A,DB⊥AB于B,
∴∠A=∠B=90°,
设运动x分钟后△CAP与△PQB全等;
则BP=xm,BQ=2xm,则AP=(12﹣x)m,
分两种情况:
①若BP=AC,则x=4,
AP=12﹣4=8,BQ=8,AP=BQ,
∴△CAP≌△PBQ;
②若BP=AP,则12﹣x=x,
解得:x=6,BQ=12≠AC,
此时△CAP与△PQB不全等;
综上所述:运动4分钟后△CAP与△PQB全等;
故答案为:4.
21.解:在Rt△AEC和Rt△DAB中
∴Rt△AEC≌Rt△DAB(HL),
∴∠ACE=∠ABD,
∵∠EAC+∠ACE=90°,
∴∠EAC+∠ABD=90°,
∴∠AFB=90°,即∠CFD=90°,
∴∠ACD+∠BDC=90°,
故答案为90.
22.解:在Rt△ADB与Rt△ADC中,
,
∴Rt△ADB≌Rt△ADC,
∴S△ABC=2S△ABD=2×AB?DE=AB?DE=3AB,
∵S△ABC=AC?BF,
∴AC?BF=3AB,
∵AC=AB,
∴BF=3,
∴BF=6.
故答案为6.
23.解:(1)△APB是直角三角形,
理由如下:∵AB=AC,∠B=30°,
∴∠C=30°=∠B=∠APQ,
∵PQ∥AC,
∴∠BPQ=∠C,
∴∠APB=60°,
∴∠BAP=90°,
∴△APB是直角三角形;
(2)当AQ=QP时,
∴∠QAP=∠APQ=30°,
∴∠BQP=∠QAP+∠APQ=60°,
当AP=PQ时,则∠AQP=∠PAQ=75°,
∴∠BQP=105°,
当AQ=AP时,则∠AQP=∠APQ=30°,
∵P不与B、C重合,
∴不存在,
综上所述:∠BQP=105°或60°.
24.(1)证明:∵AD是∠BAC的平分线,
∴∠CAD=∠BAD,
∵AB=BD,
∴∠BDA=∠BAD,
∴∠CAD=∠BDA,
∴AC∥BD;
(2)解:作FG⊥AB于G,
在Rt△ABE中,AE=2,AB=3,
∴BE===,
∴FE=BE﹣BF=﹣=,
∵AD是∠BAC的平分线,BE⊥AC,作FG⊥AB,
∴FG=FE=,即△ABF中AB边上的高为.
25.证明:(1)∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°.
∵DE∥AB,
∴∠B=EDC=60°,∠A=∠CED=60°,
∴∠EDC=∠ECD=∠DEC=60°,
∵EF⊥ED,
∴∠DEF=90°,
∴∠F=30°
∵∠F+∠FEC=∠ECD=60°,
∴∠F=∠FEC=30°,
∴CE=CF.
(2)由(1)可知∠EDC=∠ECD=∠DEC=60°,
∴CE=DC=2.
又∵CE=CF,
∴CF=2.
∴DF=DC+CF=2+2=4.
26.解:(1)∠BAD=180°﹣∠ABD﹣∠BDA=180°﹣40°﹣115°=25°;
从图中可以得知,点D从B向C运动时,∠BDA逐渐变小;
故答案为:25°;小.
(2∵∠EDC+∠EDA=∠DAB+∠B,∠B=∠EDA=40°,
∴∠EDC=∠DAB.,
∵∠B=∠C,
∴当DC=AB=2时,△ABD≌△DCE,
(3)∵AB=AC,
∴∠B=∠C=40°,
①当AD=AE时,∠ADE=∠AED=40°,
∵∠AED>∠C,
∴此时不符合;
②当DA=DE时,即∠DAE=∠DEA=(180°﹣40°)=70°,
∵∠BAC=180°﹣40°﹣40°=100°,
∴∠BAD=100°﹣70°=30°;
∴∠BDA=180°﹣30°﹣40°=110°;
③当EA=ED时,∠ADE=∠DAE=40°,
∴∠BAD=100°﹣40°=60°,
∴∠BDA=180°﹣60°﹣40°=80°;
∴当∠ADB=110°或80°时,△ADE是等腰三角形.
27.解:(1)∵CD⊥AB,
∴∠CDB=90°,
∴∠B+∠BCD=90°,
∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∴∠ACD=∠B,
∵AE平分∠BAC,
∴∠CAE=∠BAE,
∴∠ACD+∠CAE=∠B+∠BAE,
即∠CFE=∠CEF,
∴CF=CE,
即△CEF是等腰三角形;
(2)AB=2AC,
理由是:∵E在线段AB的垂直平分线上,
∴AE=BE,
∴∠B=∠BAE,
∵∠CAE=∠BAE,∠ACB=90°,
∴3∠B=90°,
∴∠B=30°,
∴AB=2AC;
(3)方法一、过E作EM⊥AB于M,
∵AC=2.5,∠ACB=90°,∠B=∠CAE=30°,
∴AE=2CE,
设CE=2,则AE=2x,
由勾股定理得:AC2+CE2=AE2,
即2.52+x2=(2x)2,
解得:x=,
即CE=,
∵AE平分∠CAB,∠ACB=90°,EM⊥AB,
∴EM=CE=,
∴△ABE的面积S==5×=;
方法二、由勾股定理得:BC=2.5,
∵CE=,
∴BE=BC﹣CE=,
∴△ABE的面积S==××2.5=.
28.(1)证明:过点D作DN⊥BA,DK⊥AC,DM⊥BC,垂足分别为点N、K、M.
∵BD、CD分别平分∠EBA、∠ECA,DN⊥BA,DK⊥AC,DM⊥BC,
∴DM=DN=DK,
∴AD平分∠GAC,∠ABD=∠DBC,
∴∠GAD=∠DAC,
∴AD平分∠GAC.
(2)证明:∵∠GAC=∠ABC+∠ACB,∠GAD=∠DAC,
又∵AB=AC,
∴∠ABC=∠ACB,
∴∠GAD=∠ABC,
∴AD∥BC.
29.证明:连接DF,
∵∠BCE+∠ACE=90°,∠ACE+∠CAE=90°,
∴∠BCE=∠CAE.
∵AC⊥BC,BF∥AC.
∴BF⊥BC.
∴∠ACD=∠CBF=90°,
∵AC=CB,
∴△ACD≌△CBF.∴CD=BF.
∵CD=BD=BC,∴BF=BD.
∴△BFD为等腰直角三角形.
∵∠ACB=90°,CA=CB,
∴∠ABC=45°.
∵∠FBD=90°,
∴∠ABF=45°.
∴∠ABC=∠ABF,即BA是∠FBD的平分线.
∴BA是FD边上的高线,BA又是边FD的中线,
即AB垂直平分DF.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
