苏科版八年级下册数学 8.3频率与概率(1) 课件(31张)
文档属性
| 名称 | 苏科版八年级下册数学 8.3频率与概率(1) 课件(31张) |  | |
| 格式 | ppt | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 16:04:01 | ||
图片预览









文档简介
初中数学八年级下册
(苏科版)
8.3 频率与概率(1)
青春最宝贵的东西,是无所畏惧的勇气和尚未定型的可能性!有梦就去追!不用等风来!你自己就能飞!
老师寄语:
初中数学八年级下册
(苏科版)
8.3 频率与概率(1)
张榕芳
泗洪育才实验学校
频数:
某个对象出现的次数。
频率:
频数与总次数的比值。
一家保险公司要为购买机票的旅客进行保险,应该收取多少保险费呢?
为此,必须得计算出飞机失事的可能性大小!
想知道一批乒乓球是否合格?
就得知道它是优等品的可能性有多大!
据说以前火箭队每次有技术犯规的罚球机会,都 会让姚明去,这是为什么呢?
他投球命中的可能性有多大呢?
仅仅了解随机事件可能性有大有小是不够的,我们需要定量的研究这个可能性到底有多大!这就需要寻找一个量来刻画随机事件发生的可能性大小!
能表示可能性大小数值的词叫什么呢?
一个事件发生可能性大小的数值,称为这个事件的概率。
如果用A表示一个事件,那么我们就用P(A)表示事件A发生的概率.
概率:
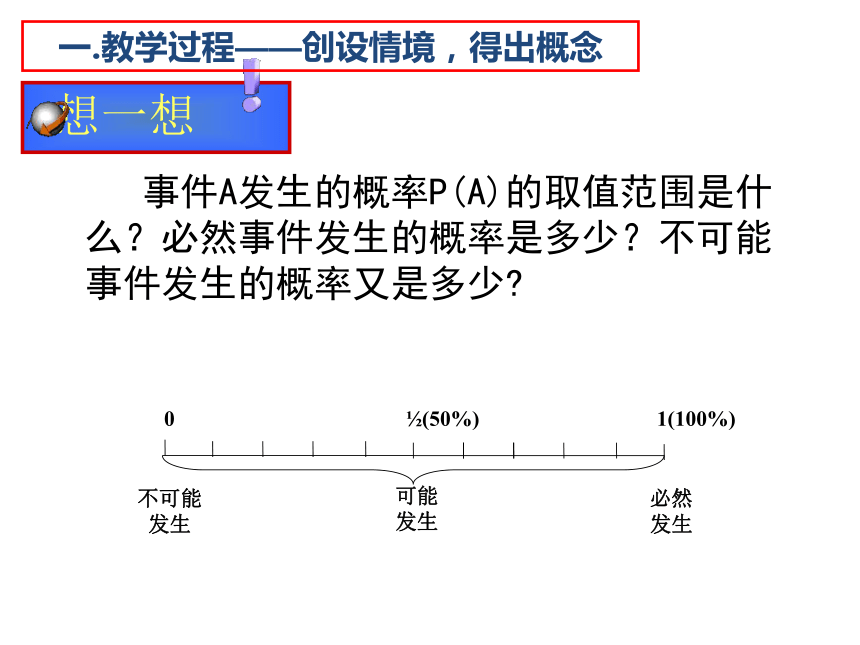
事件A发生的概率P(A)的取值范围是什么?必然事件发生的概率是多少?不可能事件发生的概率又是多少?
想一想
0 ?(50%) 1(100%)
不可能发生
可能发生
必然发生
0.83
但是我们用什么方法知道一个随机事件发生的概率呢?
这些事情的概率你知道吗?
0.92
在数学中,我们发现真理的主要工具是归纳和模拟。
———拉普拉斯
拉普拉斯(1749-1827)
法国数学家,物理学家
分析学家,概率论家,法国科学院院士。
正 面
反 面
猜想:你觉得多次实验后正面向上的频率会正好是0.5吗?
实践探索一
实践探索一
本实验两人一小组,共分为三个环节:
环节一:记录小组内频数(比协调合作)
环节二:汇总频数与频率(比精准计算)
环节三:完成折线统计图(比仔细认真)
注意:实验结果必须真实准确,表现积极踊跃的同学将获得小奖品!
为了节省时间和尽可能条件的统一,我们约定:
①两人一组, 一人掷币,一人记录正面向上的次数。
②每组各掷一枚硬币10次。
③把频数记录在学案的第一个表格上,完成较快的 前16组同学把数据填到黑板上。
抛掷次数
10
10
10
10
10
10
10
10
10
.....
正面朝上的次数
环节一:记录小组频数,比协调合作
实践探索一
把各组同学的结果汇总,填写下表:(频率保留两位小数)
汇总组数
第1组
前2组
前4组
前6组
前8组
前10组
前12组
前14组
前16组
抛掷次数(n)
10
20
40
60
80
100
120
140
160
频数(m)
频率( )
实践探索一
环节二:汇总频数与频率,比精准计算
环节三:完成折线统计图,比仔细认真
讨论:随着投掷次数的增加折线有什么样的变化趋势?频率会稳定在一个常数附近吗?实验前你的猜想得到验证了吗?
哈尔莫斯(1916-2006)
美国数学家,概率论家
“数学的创作绝不是单靠推论可以得到的,首先通常是一些模糊的猜测,揣摩着可能的推广,接着下了不十分有把握的结论。然后整理想法,直到看出事实的端倪,往往还要费好大的劲儿,才能将一切付诸逻辑式的证明。这过程并不是一蹴可几的,要经过许多失败、挫折,一再地猜测、揣摹,在试探中白花掉几个月的时间是常有的。”
————哈尔莫斯
试验者
抛掷次数(n)
“正面向上”次数(m)
“正面向上”频率
棣莫弗
布丰
费勒
皮尔逊
皮尔逊
2 048
4 040
10 000
12 000
24 000
1 061
2 048
4 979
6 019
12 012
0.5180
0.506 9
0.497 9
0.501 6
0.500 5
棣莫弗 (1667—1754)
布丰(1707—1788)
费勒(1906—1970)
皮尔逊 (1857—1936)
参照折线图用自己的话说说:多次重复实验时频率有什么特点?
绘制成折线统计图:
通常,在多次重复实验中,一个随机事件的频率一般会在一个常数附近摆动,并且趋于稳定。这个性质称为频率的
稳定性。
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
50
100
150
200
250
300
350
400
450
500
频率
抛掷次数
p
n足够大
瑞士数学家雅各布·伯努利(1654—1705)最早
阐明频率具有稳定性。
1994年瑞士发行了雅各布·伯努利的纪念邮票,图案中有以他名字命名的大数定律的示意图.(在多次重复试验中,事件出现的频率稳定于其出现的概率.)
p
n足够大
P(A)
A.频率就是概率。
B.频率是随机的。
C连续抛硬币10次有可能都正面朝上。
D随着实验次数的增加,频率一般会越来越接近概率。
A
2.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个,小明做摸球实验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(1)补全表格和折线统计图
(2)请估计:当n很大时,摸到白球的频率稳定值约为______(精确到0.1)
(3)估算盒子里有白球_______个.
摸球的次数n
100
200
300
500
800
1000
1500
摸到白球的次数m
70
171
302
481
599
903
摸到白球的频率( )
0.700
0.640
0.570
0.604
0.601
0.602
128
0.599
实践探索二
2.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个,小明做摸球实验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(1)补全表格和折线统计图
(2)请估计:当n很大时,摸到白球的频率稳定值约为______(精确到0.1)
(2)估算盒子里有白球_______个.
摸球的次数n
100
200
300
500
800
1000
1500
摸到白球的次数m
70
128
171
302
481
599
903
摸到白球的频率( )
0.700
0.640
0.570
0.604
0.601
0.599
0.602
0.6
24
实践探索二
2.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个,小明做摸球实验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(4)若向盒子里再放入x个除颜色以外其它完全相同的球,这x个球中白球只有1个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回,通过大量重复摸球试验后发现,摸到白球的频率稳定在50%,那么可以推测出x最有可能是________.
摸球的次数n
100
200
300
500
800
1000
1500
摸到白球的次数m
70
128
171
302
481
599
903
摸到白球的频率( )
0.700
0.640
0.570
0.604
0.601
0.599
0.602
10
实践探索二
8.3 频率与概率
p
n足够大
P(A)
3.观察上面两幅漫画,如果你是“小黄”同学,遇到这样的情况你是怎么想的呢?跟周围同学讨论讨论吧!
明白一种性质……
在多次重复实验中,一个随机事件的频率会在一个常数附近摆动,并且趋于稳定。这个性质称为频率的稳定性!
.
知道一种概念……
了解一种方法……
概率:一个事件发生可能性大小的数值。
用大量重复试验频率去估计概率
学到一种精神……
数学家们对待科学严谨的态度和锲而不舍追求真理的精神!
放飞梦想,展翅翱翔
人生中最重要的问题,在绝大多数情况下真的就只是概率问题!
———拉普拉斯
p
n足够大
P(A)
4.如图,均匀的正四面体的各面依次标有“1,2,3,4” 四个数字,小明做了60次投掷试验,结果统计如下:
(1)计算上述试验中“4朝下”的频率是________;
(2)“根据试验结果,投掷一次正四面体,出现2朝下的概率是 “ ”的说法正确吗?为什么?
不正确。只有当实验次数很大时,事情发生的频率才会稳定在概率附近。
通常,在多次重复实验中,一个随机事件的频率一般会在一个常数附近摆动,并且趋于稳定。这个性质称为频率的
稳定性。
把各组同学的结果汇总,填写下表:(频率保留两位小数)
汇总组数
第1组
前2组
前4组
前6组
前8组
前10组
前12组
前14组
抛掷次数(n)
10
20
40
60
80
100
120
140
频数(m)
频率( )
实践探索一
环节二:汇总频数与频率,比精准计算
环节三:完成折线统计图,比仔细认真
讨论:随着投掷次数的增加折线有什么样的变化趋势?频率会稳定在一个常数附近吗?实验前你的猜想得到验证了吗?
(苏科版)
8.3 频率与概率(1)
青春最宝贵的东西,是无所畏惧的勇气和尚未定型的可能性!有梦就去追!不用等风来!你自己就能飞!
老师寄语:
初中数学八年级下册
(苏科版)
8.3 频率与概率(1)
张榕芳
泗洪育才实验学校
频数:
某个对象出现的次数。
频率:
频数与总次数的比值。
一家保险公司要为购买机票的旅客进行保险,应该收取多少保险费呢?
为此,必须得计算出飞机失事的可能性大小!
想知道一批乒乓球是否合格?
就得知道它是优等品的可能性有多大!
据说以前火箭队每次有技术犯规的罚球机会,都 会让姚明去,这是为什么呢?
他投球命中的可能性有多大呢?
仅仅了解随机事件可能性有大有小是不够的,我们需要定量的研究这个可能性到底有多大!这就需要寻找一个量来刻画随机事件发生的可能性大小!
能表示可能性大小数值的词叫什么呢?
一个事件发生可能性大小的数值,称为这个事件的概率。
如果用A表示一个事件,那么我们就用P(A)表示事件A发生的概率.
概率:
事件A发生的概率P(A)的取值范围是什么?必然事件发生的概率是多少?不可能事件发生的概率又是多少?
想一想
0 ?(50%) 1(100%)
不可能发生
可能发生
必然发生
0.83
但是我们用什么方法知道一个随机事件发生的概率呢?
这些事情的概率你知道吗?
0.92
在数学中,我们发现真理的主要工具是归纳和模拟。
———拉普拉斯
拉普拉斯(1749-1827)
法国数学家,物理学家
分析学家,概率论家,法国科学院院士。
正 面
反 面
猜想:你觉得多次实验后正面向上的频率会正好是0.5吗?
实践探索一
实践探索一
本实验两人一小组,共分为三个环节:
环节一:记录小组内频数(比协调合作)
环节二:汇总频数与频率(比精准计算)
环节三:完成折线统计图(比仔细认真)
注意:实验结果必须真实准确,表现积极踊跃的同学将获得小奖品!
为了节省时间和尽可能条件的统一,我们约定:
①两人一组, 一人掷币,一人记录正面向上的次数。
②每组各掷一枚硬币10次。
③把频数记录在学案的第一个表格上,完成较快的 前16组同学把数据填到黑板上。
抛掷次数
10
10
10
10
10
10
10
10
10
.....
正面朝上的次数
环节一:记录小组频数,比协调合作
实践探索一
把各组同学的结果汇总,填写下表:(频率保留两位小数)
汇总组数
第1组
前2组
前4组
前6组
前8组
前10组
前12组
前14组
前16组
抛掷次数(n)
10
20
40
60
80
100
120
140
160
频数(m)
频率( )
实践探索一
环节二:汇总频数与频率,比精准计算
环节三:完成折线统计图,比仔细认真
讨论:随着投掷次数的增加折线有什么样的变化趋势?频率会稳定在一个常数附近吗?实验前你的猜想得到验证了吗?
哈尔莫斯(1916-2006)
美国数学家,概率论家
“数学的创作绝不是单靠推论可以得到的,首先通常是一些模糊的猜测,揣摩着可能的推广,接着下了不十分有把握的结论。然后整理想法,直到看出事实的端倪,往往还要费好大的劲儿,才能将一切付诸逻辑式的证明。这过程并不是一蹴可几的,要经过许多失败、挫折,一再地猜测、揣摹,在试探中白花掉几个月的时间是常有的。”
————哈尔莫斯
试验者
抛掷次数(n)
“正面向上”次数(m)
“正面向上”频率
棣莫弗
布丰
费勒
皮尔逊
皮尔逊
2 048
4 040
10 000
12 000
24 000
1 061
2 048
4 979
6 019
12 012
0.5180
0.506 9
0.497 9
0.501 6
0.500 5
棣莫弗 (1667—1754)
布丰(1707—1788)
费勒(1906—1970)
皮尔逊 (1857—1936)
参照折线图用自己的话说说:多次重复实验时频率有什么特点?
绘制成折线统计图:
通常,在多次重复实验中,一个随机事件的频率一般会在一个常数附近摆动,并且趋于稳定。这个性质称为频率的
稳定性。
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
50
100
150
200
250
300
350
400
450
500
频率
抛掷次数
p
n足够大
瑞士数学家雅各布·伯努利(1654—1705)最早
阐明频率具有稳定性。
1994年瑞士发行了雅各布·伯努利的纪念邮票,图案中有以他名字命名的大数定律的示意图.(在多次重复试验中,事件出现的频率稳定于其出现的概率.)
p
n足够大
P(A)
A.频率就是概率。
B.频率是随机的。
C连续抛硬币10次有可能都正面朝上。
D随着实验次数的增加,频率一般会越来越接近概率。
A
2.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个,小明做摸球实验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(1)补全表格和折线统计图
(2)请估计:当n很大时,摸到白球的频率稳定值约为______(精确到0.1)
(3)估算盒子里有白球_______个.
摸球的次数n
100
200
300
500
800
1000
1500
摸到白球的次数m
70
171
302
481
599
903
摸到白球的频率( )
0.700
0.640
0.570
0.604
0.601
0.602
128
0.599
实践探索二
2.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个,小明做摸球实验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(1)补全表格和折线统计图
(2)请估计:当n很大时,摸到白球的频率稳定值约为______(精确到0.1)
(2)估算盒子里有白球_______个.
摸球的次数n
100
200
300
500
800
1000
1500
摸到白球的次数m
70
128
171
302
481
599
903
摸到白球的频率( )
0.700
0.640
0.570
0.604
0.601
0.599
0.602
0.6
24
实践探索二
2.在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个,小明做摸球实验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(4)若向盒子里再放入x个除颜色以外其它完全相同的球,这x个球中白球只有1个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回,通过大量重复摸球试验后发现,摸到白球的频率稳定在50%,那么可以推测出x最有可能是________.
摸球的次数n
100
200
300
500
800
1000
1500
摸到白球的次数m
70
128
171
302
481
599
903
摸到白球的频率( )
0.700
0.640
0.570
0.604
0.601
0.599
0.602
10
实践探索二
8.3 频率与概率
p
n足够大
P(A)
3.观察上面两幅漫画,如果你是“小黄”同学,遇到这样的情况你是怎么想的呢?跟周围同学讨论讨论吧!
明白一种性质……
在多次重复实验中,一个随机事件的频率会在一个常数附近摆动,并且趋于稳定。这个性质称为频率的稳定性!
.
知道一种概念……
了解一种方法……
概率:一个事件发生可能性大小的数值。
用大量重复试验频率去估计概率
学到一种精神……
数学家们对待科学严谨的态度和锲而不舍追求真理的精神!
放飞梦想,展翅翱翔
人生中最重要的问题,在绝大多数情况下真的就只是概率问题!
———拉普拉斯
p
n足够大
P(A)
4.如图,均匀的正四面体的各面依次标有“1,2,3,4” 四个数字,小明做了60次投掷试验,结果统计如下:
(1)计算上述试验中“4朝下”的频率是________;
(2)“根据试验结果,投掷一次正四面体,出现2朝下的概率是 “ ”的说法正确吗?为什么?
不正确。只有当实验次数很大时,事情发生的频率才会稳定在概率附近。
通常,在多次重复实验中,一个随机事件的频率一般会在一个常数附近摆动,并且趋于稳定。这个性质称为频率的
稳定性。
把各组同学的结果汇总,填写下表:(频率保留两位小数)
汇总组数
第1组
前2组
前4组
前6组
前8组
前10组
前12组
前14组
抛掷次数(n)
10
20
40
60
80
100
120
140
频数(m)
频率( )
实践探索一
环节二:汇总频数与频率,比精准计算
环节三:完成折线统计图,比仔细认真
讨论:随着投掷次数的增加折线有什么样的变化趋势?频率会稳定在一个常数附近吗?实验前你的猜想得到验证了吗?
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
