18.1.2平行四边形的判定(边角)-2020-2021学年人教版八年级数学下册导学案(含详解)
文档属性
| 名称 | 18.1.2平行四边形的判定(边角)-2020-2021学年人教版八年级数学下册导学案(含详解) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 16:08:20 | ||
图片预览


文档简介
18.1.2
平行四边形的判定(1)
学习目标:
1.经历平行四边形判定定理的猜想与证明过程,体会类比思想及探究图形判定的一般思路;
2.会根据不同条件灵活选取适当的判定定理进行推理论证.
学习重点:根据边角条件判定平行四边形.
一、课前检测
二、温故知新
1.平行四边形的定义是什么?它有什么作用?
2.
除了两组对边分别平行,平行四边形还有哪些性质?请分别用符号语言表示
3.平行四边形上面的三条性质的逆命题各是什么?
三、预习导航(预习教材第45页,标出你认为重要的关键词)
猜一猜
将两长两短的四根细木条用小钉固定在一起,任意拉动,所得的四边形是平行四边形吗?
证一证
已知:
四边形ABCD中,AB=DC,AD=BC.
求证:
四边形ABCD是平行四边形.
证明:
连接AC,
在△ABC和△CDA中,
AB=CD
,
AC=CA,
∴△ABC_____△CDA(________).
BC=DA,
∴
∠1____∠4
,
∠
2_____∠3,
∴AB_____CD
,
AD_____BC,
∴四边形ABCD是________________.
要点归纳:平行四边形的判定定理:两组对边分别_________的四边形是平行四边形.
几何语言描述:在四边形ABCD中,∵AB=CD,AD=BC,
∴四边形ABCD是_________________.
反思:连接AC有什么作用?体现了什么数学思想?
四、自学自测
在如图所示的四边形PONM中,其中∠MON=90°.
求证:四边形PONM是平行四边形.
五、我的疑惑(反思)
1、要点探究
探究点1:从边的条件判定平行四边形
由预习导航可知:两组对边_____________的四边形是平行四边形.
它是平行四边形的第一个判定定理,在证明或计算中有着广泛的应用.
学以致用
如图
□ABCD的对角线AC、BD交于点O,E、F是AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
探究点2:从角的条件判定平行四边形
猜一猜
对于两组对角分别相等的四边形的形状,你的猜想是什么?
证一证
已知:四边形ABCD中,∠A=∠C,∠B=∠D,
求证:四边形ABCD是平行四边形.
证明:∵∠A+∠C+∠B+∠D=_______°,
又∵∠A=∠C,∠B=∠D,
∴___∠A+___∠B=_______°,
即∠A+∠B=______°,
∴
AD_____BC.同理得
AB_____CD,
∴四边形ABCD是________________.
要点归纳:平行四边形的判定定理:两组对角分别________的四边形是平行四边形.
几何语言描述:在四边形ABCD中,∵∠A=______,∠B=______,
∴四边形ABCD是_______________.
即学即练
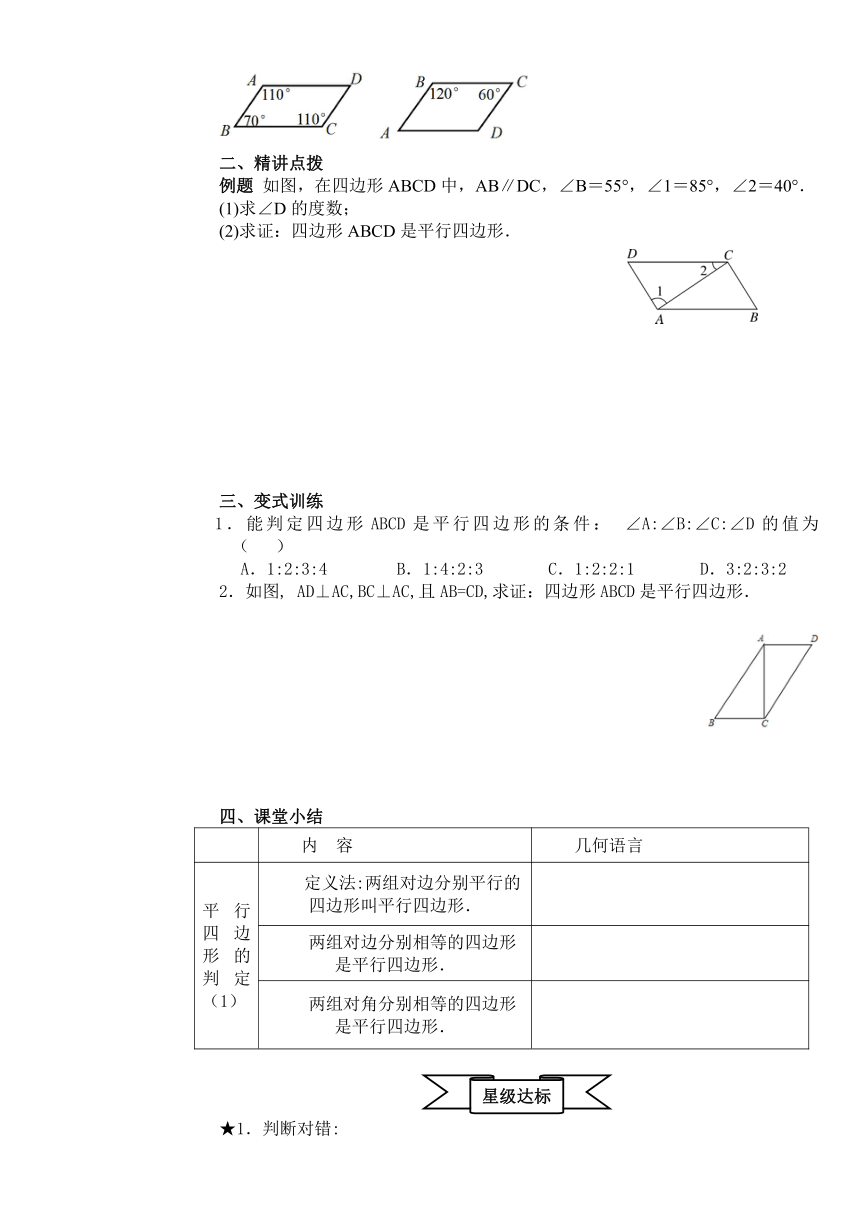
判断下列四边形是否为平行四边形:
二、精讲点拨
例题
如图,在四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
三、变式训练
1.能判定四边形ABCD是平行四边形的条件:
∠A:∠B:∠C:∠D的值为
(
)
A.1:2:3:4
B.1:4:2:3
C.1:2:2:1
D.3:2:3:2
2.如图,
AD⊥AC,BC⊥AC,且AB=CD,求证:四边形ABCD是平行四边形.
四、课堂小结
内
容
几何语言
平行四边形的判定(1)
定义法:两组对边分别平行的四边形叫平行四边形.
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
★1.判断对错:
(1)有一组对边平行的四边形是平行四边形
(
)
(2)有两条边相等,并且另外的两条边也相等的四边形是平行四边形(
)
(3)有一组对角相等且一组对边平行的四边形是平行四边形
(
)
★2.如图,在四边形ABCD中,
(1)如果AB∥CD,AD∥BC,那么四边形ABCD是
__________.
(2)如果∠A:∠B:∠
C:∠D=a:b:a:b(a,b为正数),那
么四边形ABCD是__________.
(3)如果AD=6cm,AB=4cm,那么当BC=_______cm,CD=_____cm时,四边形ABCD为平行四边形.
★3.在□ABCD中,∠BAD,∠BCD的平分线分别交BC,AD于点F,E.
求证:四边形AFCE是平行四边形.
★★4.如图,五边形ABCDE是正五边形,连接BD、CE,交于点P.
求证:四边形ABPE是平行四边形.
★★★5.如图,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD、等边△ACE、等边△BCF.试说明四边形DAEF是平行四边形.
我的反思(收获,不足)
分层作业
必做(教材
智慧学习
配套)
选做
参考答案:
自学自测
试题分析:本题考查平行四边形的判定方法,在Rt△MON中,利用勾股定理构造方程求出x的值,进而求出各边长,可以得到PM=ON,MN=OP.根据两组对边分别相等的四边形是平行四边形可证得结论.
【详解】
证明:在Rt△MON中,由勾股定理,得:
,即.
解得x=8.
∴ON=x-5=3,MN=x-3=5,PM=11-x=3.
∴PM=ON,MN=OP.
∴四边形PONM是平行四边形.
学以致用
试题分析:要证明四边形BFDE是平行四边形,可以证四边形BFDE有两组对边分别相等,即证明BF=DE,EB=DF即可得到.
【详解】
证明:∵ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠BAF=∠DCE,
又∵对角线AC与BD相交于O,E.F是AC上的两点,并且AE=CF,
所以在△ABF和△DCE中,
,
∴△ABF≌△CDE(SAS),∴BF=DE,
同理可证:△ADF≌△CBE(SAS),∴DF=BE,
∴四边形BFDE是平行四边形.
即学即练
试题分析:根据两组对角分别相等的四边形是平行四边形进行判断.
详解:左图中∠D=360°-∠A-∠B-∠C=360°-110°-70°-110°=70°.
∴∠A=∠C,∠B=∠D.故左图是平行四边形.
右图中∠B=120°,∠C=60°,∠B+∠C=180°
∴AB∥CD.
但不能判定是否为平行四边形.
精讲点拨
例题
试题分析:(1)根据三角形内角和为180°,可得结果;(2)根据平行线性质求出∠ACB
=85°,由∠ACB=∠1=85°得AD∥BC.两组对边平行的四边形是平行四边形.
【详解】(1)在△ACD中,∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=180°-40°-85°=55°.
(2)证明:∵AB∥DC,
∴∠2+∠ACB+∠B=180°.
∴∠ACB=180°-∠B-∠2
=180°-55°-40°=85°.
∵∠ACB=∠1=85°,
∴AD∥BC.
又∵AB∥DC
∴四边形ABCD是平行四边形.
变式训练
1、试题分析:从角的方面判定平行四边形的方法:对角相等的四边形是平行四边形.
【详解】
两组对角分别相等的四边形是平行四边形,所以∠A和∠C是对角,∠B和∠D是对角,对角的份数应相等.只有选项D符合.
2、试题分析:从条件AD⊥AC,BC⊥AC,可知∠CAD=∠ACB=90°,再结合AB=CD,AC为公共边,可得△ACD≌△CAB,于是AD=CB.根据两组对边分别相等的四边形是平行四边形证.
【详解】
证明:∵AD⊥AC,BC⊥AC,∴∠CAD=∠ACB=90°.
在Rt△ACD和Rt△CAB中
∴Rt△ACD≌Rt△CAB.
∴AD=CB.又∵AB=CD
∴四边形ABCD是平行四边形.
星级达标
1.试题分析:根据平行四边形的判定方法进行判断即可.
详解:
因为有两组对边平行的四边形是平行四边形,命题(1)错误;
命题(2)中没有说明相等的两边是对边,故不正确;
命题(3)从一组对边平行,可得两组同旁内角互补,再结合有一组对角相等,得另一组对角也相等,故该四边形是平行四边形.故命题(3)正确.
故答案为:(1)×(2)×(3)√
2、试题分析:根据平行四边形的判定方法进行判断填空即可.
详解:(1)根据平行四边形的定义可知四边形ABCD是平行四边形;
(2)从∠A:∠B:∠
C:∠D=a:b:a:b可知∠A=∠C,∠B=∠D,根据两组对角分别相等的四边形是平行四边形,可知四边形ABCD是平行四边形;
(3)因为两组对边分别相等的四边形是平行四边形,故BC=AD=6cm,CD=AB=4cm时,四边形ABCD是平行四边形.
故答案为:(1)平行四边形;(2)平行四边形;(3)6,4.
3、试题分析:根据角平分线的定义以及平行线的性质,证明∠1=∠2,再由平行线的性质,得到∠3=∠4,即可得到结论.
【详解】
证明:∵ABCD是平行四边形,∴AD∥BC,∠BAD=∠BCD.
∵AF、CE分别平分∠BAD、∠BCD,
∴∠1=∠BAD,∠2=∠BCD,
∴∠1=∠2.
∵AD∥BC,
∴∠1+∠3=1800 ∠2+∠4=180°,
∴∠3=∠4.又∵∠1=∠2,
∴AFCE是平行四边形.
4、试题分析:用同旁内角互补,两直线平行,分别证明AE∥BP,AB∥EP,即可得到四边形ABPE是平行四边形.
【详解】
证明:∵五边形ABCDE是正五边形,
∴∠A=∠BCD=∠ABC=(5-2)×180°÷5=108°,CB=CD,
∴∠CBD=(180°-108°)÷2=36°,
∴∠ABD=∠ABC-∠CBD=108°-36°=72°,
∴∠A+∠ABD=108°+72°=180°,
∴AE∥BP,
同理AB∥EP,
∴四边形ABPE是平行四边形.
5、试题分析:根据已知条件易证△ABC≌△DBF,根据全等三角形的性质可得AC=DF;同理可证得AB=EF.即可得EF=AD,DF=AE,根据两组对边分别相等的四边形是平行四边形即可证得结论.
【详解】
证明:∵△ABD和△BCF都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,BD=BA,BF=BC,
∴∠DBF=∠ABC.
∴△ABC≌△DBF,∴AC=DF.
又∵AC=AE,∴DF=AE.
同理可证得△ABC≌△EFC,∴AB=EF.
又∵AB=AD,∴EF=AD,
∴四边形DAEF是平行四边形.
自主研习
探究点拨
星级达标
平行四边形的判定(1)
学习目标:
1.经历平行四边形判定定理的猜想与证明过程,体会类比思想及探究图形判定的一般思路;
2.会根据不同条件灵活选取适当的判定定理进行推理论证.
学习重点:根据边角条件判定平行四边形.
一、课前检测
二、温故知新
1.平行四边形的定义是什么?它有什么作用?
2.
除了两组对边分别平行,平行四边形还有哪些性质?请分别用符号语言表示
3.平行四边形上面的三条性质的逆命题各是什么?
三、预习导航(预习教材第45页,标出你认为重要的关键词)
猜一猜
将两长两短的四根细木条用小钉固定在一起,任意拉动,所得的四边形是平行四边形吗?
证一证
已知:
四边形ABCD中,AB=DC,AD=BC.
求证:
四边形ABCD是平行四边形.
证明:
连接AC,
在△ABC和△CDA中,
AB=CD
,
AC=CA,
∴△ABC_____△CDA(________).
BC=DA,
∴
∠1____∠4
,
∠
2_____∠3,
∴AB_____CD
,
AD_____BC,
∴四边形ABCD是________________.
要点归纳:平行四边形的判定定理:两组对边分别_________的四边形是平行四边形.
几何语言描述:在四边形ABCD中,∵AB=CD,AD=BC,
∴四边形ABCD是_________________.
反思:连接AC有什么作用?体现了什么数学思想?
四、自学自测
在如图所示的四边形PONM中,其中∠MON=90°.
求证:四边形PONM是平行四边形.
五、我的疑惑(反思)
1、要点探究
探究点1:从边的条件判定平行四边形
由预习导航可知:两组对边_____________的四边形是平行四边形.
它是平行四边形的第一个判定定理,在证明或计算中有着广泛的应用.
学以致用
如图
□ABCD的对角线AC、BD交于点O,E、F是AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形.
探究点2:从角的条件判定平行四边形
猜一猜
对于两组对角分别相等的四边形的形状,你的猜想是什么?
证一证
已知:四边形ABCD中,∠A=∠C,∠B=∠D,
求证:四边形ABCD是平行四边形.
证明:∵∠A+∠C+∠B+∠D=_______°,
又∵∠A=∠C,∠B=∠D,
∴___∠A+___∠B=_______°,
即∠A+∠B=______°,
∴
AD_____BC.同理得
AB_____CD,
∴四边形ABCD是________________.
要点归纳:平行四边形的判定定理:两组对角分别________的四边形是平行四边形.
几何语言描述:在四边形ABCD中,∵∠A=______,∠B=______,
∴四边形ABCD是_______________.
即学即练
判断下列四边形是否为平行四边形:
二、精讲点拨
例题
如图,在四边形ABCD中,AB∥DC,∠B=55°,∠1=85°,∠2=40°.
(1)求∠D的度数;
(2)求证:四边形ABCD是平行四边形.
三、变式训练
1.能判定四边形ABCD是平行四边形的条件:
∠A:∠B:∠C:∠D的值为
(
)
A.1:2:3:4
B.1:4:2:3
C.1:2:2:1
D.3:2:3:2
2.如图,
AD⊥AC,BC⊥AC,且AB=CD,求证:四边形ABCD是平行四边形.
四、课堂小结
内
容
几何语言
平行四边形的判定(1)
定义法:两组对边分别平行的四边形叫平行四边形.
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
★1.判断对错:
(1)有一组对边平行的四边形是平行四边形
(
)
(2)有两条边相等,并且另外的两条边也相等的四边形是平行四边形(
)
(3)有一组对角相等且一组对边平行的四边形是平行四边形
(
)
★2.如图,在四边形ABCD中,
(1)如果AB∥CD,AD∥BC,那么四边形ABCD是
__________.
(2)如果∠A:∠B:∠
C:∠D=a:b:a:b(a,b为正数),那
么四边形ABCD是__________.
(3)如果AD=6cm,AB=4cm,那么当BC=_______cm,CD=_____cm时,四边形ABCD为平行四边形.
★3.在□ABCD中,∠BAD,∠BCD的平分线分别交BC,AD于点F,E.
求证:四边形AFCE是平行四边形.
★★4.如图,五边形ABCDE是正五边形,连接BD、CE,交于点P.
求证:四边形ABPE是平行四边形.
★★★5.如图,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD、等边△ACE、等边△BCF.试说明四边形DAEF是平行四边形.
我的反思(收获,不足)
分层作业
必做(教材
智慧学习
配套)
选做
参考答案:
自学自测
试题分析:本题考查平行四边形的判定方法,在Rt△MON中,利用勾股定理构造方程求出x的值,进而求出各边长,可以得到PM=ON,MN=OP.根据两组对边分别相等的四边形是平行四边形可证得结论.
【详解】
证明:在Rt△MON中,由勾股定理,得:
,即.
解得x=8.
∴ON=x-5=3,MN=x-3=5,PM=11-x=3.
∴PM=ON,MN=OP.
∴四边形PONM是平行四边形.
学以致用
试题分析:要证明四边形BFDE是平行四边形,可以证四边形BFDE有两组对边分别相等,即证明BF=DE,EB=DF即可得到.
【详解】
证明:∵ABCD是平行四边形,
∴AB=DC,AB∥DC,
∴∠BAF=∠DCE,
又∵对角线AC与BD相交于O,E.F是AC上的两点,并且AE=CF,
所以在△ABF和△DCE中,
,
∴△ABF≌△CDE(SAS),∴BF=DE,
同理可证:△ADF≌△CBE(SAS),∴DF=BE,
∴四边形BFDE是平行四边形.
即学即练
试题分析:根据两组对角分别相等的四边形是平行四边形进行判断.
详解:左图中∠D=360°-∠A-∠B-∠C=360°-110°-70°-110°=70°.
∴∠A=∠C,∠B=∠D.故左图是平行四边形.
右图中∠B=120°,∠C=60°,∠B+∠C=180°
∴AB∥CD.
但不能判定是否为平行四边形.
精讲点拨
例题
试题分析:(1)根据三角形内角和为180°,可得结果;(2)根据平行线性质求出∠ACB
=85°,由∠ACB=∠1=85°得AD∥BC.两组对边平行的四边形是平行四边形.
【详解】(1)在△ACD中,∵∠D+∠2+∠1=180°,
∴∠D=180°-∠2-∠1=180°-40°-85°=55°.
(2)证明:∵AB∥DC,
∴∠2+∠ACB+∠B=180°.
∴∠ACB=180°-∠B-∠2
=180°-55°-40°=85°.
∵∠ACB=∠1=85°,
∴AD∥BC.
又∵AB∥DC
∴四边形ABCD是平行四边形.
变式训练
1、试题分析:从角的方面判定平行四边形的方法:对角相等的四边形是平行四边形.
【详解】
两组对角分别相等的四边形是平行四边形,所以∠A和∠C是对角,∠B和∠D是对角,对角的份数应相等.只有选项D符合.
2、试题分析:从条件AD⊥AC,BC⊥AC,可知∠CAD=∠ACB=90°,再结合AB=CD,AC为公共边,可得△ACD≌△CAB,于是AD=CB.根据两组对边分别相等的四边形是平行四边形证.
【详解】
证明:∵AD⊥AC,BC⊥AC,∴∠CAD=∠ACB=90°.
在Rt△ACD和Rt△CAB中
∴Rt△ACD≌Rt△CAB.
∴AD=CB.又∵AB=CD
∴四边形ABCD是平行四边形.
星级达标
1.试题分析:根据平行四边形的判定方法进行判断即可.
详解:
因为有两组对边平行的四边形是平行四边形,命题(1)错误;
命题(2)中没有说明相等的两边是对边,故不正确;
命题(3)从一组对边平行,可得两组同旁内角互补,再结合有一组对角相等,得另一组对角也相等,故该四边形是平行四边形.故命题(3)正确.
故答案为:(1)×(2)×(3)√
2、试题分析:根据平行四边形的判定方法进行判断填空即可.
详解:(1)根据平行四边形的定义可知四边形ABCD是平行四边形;
(2)从∠A:∠B:∠
C:∠D=a:b:a:b可知∠A=∠C,∠B=∠D,根据两组对角分别相等的四边形是平行四边形,可知四边形ABCD是平行四边形;
(3)因为两组对边分别相等的四边形是平行四边形,故BC=AD=6cm,CD=AB=4cm时,四边形ABCD是平行四边形.
故答案为:(1)平行四边形;(2)平行四边形;(3)6,4.
3、试题分析:根据角平分线的定义以及平行线的性质,证明∠1=∠2,再由平行线的性质,得到∠3=∠4,即可得到结论.
【详解】
证明:∵ABCD是平行四边形,∴AD∥BC,∠BAD=∠BCD.
∵AF、CE分别平分∠BAD、∠BCD,
∴∠1=∠BAD,∠2=∠BCD,
∴∠1=∠2.
∵AD∥BC,
∴∠1+∠3=1800 ∠2+∠4=180°,
∴∠3=∠4.又∵∠1=∠2,
∴AFCE是平行四边形.
4、试题分析:用同旁内角互补,两直线平行,分别证明AE∥BP,AB∥EP,即可得到四边形ABPE是平行四边形.
【详解】
证明:∵五边形ABCDE是正五边形,
∴∠A=∠BCD=∠ABC=(5-2)×180°÷5=108°,CB=CD,
∴∠CBD=(180°-108°)÷2=36°,
∴∠ABD=∠ABC-∠CBD=108°-36°=72°,
∴∠A+∠ABD=108°+72°=180°,
∴AE∥BP,
同理AB∥EP,
∴四边形ABPE是平行四边形.
5、试题分析:根据已知条件易证△ABC≌△DBF,根据全等三角形的性质可得AC=DF;同理可证得AB=EF.即可得EF=AD,DF=AE,根据两组对边分别相等的四边形是平行四边形即可证得结论.
【详解】
证明:∵△ABD和△BCF都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,BD=BA,BF=BC,
∴∠DBF=∠ABC.
∴△ABC≌△DBF,∴AC=DF.
又∵AC=AE,∴DF=AE.
同理可证得△ABC≌△EFC,∴AB=EF.
又∵AB=AD,∴EF=AD,
∴四边形DAEF是平行四边形.
自主研习
探究点拨
星级达标
