2020-2021学年八年级数学人教版下册第18章《平行四边形》经典常考题专题训练(一)(Word版 含解析)
文档属性
| 名称 | 2020-2021学年八年级数学人教版下册第18章《平行四边形》经典常考题专题训练(一)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 156.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 16:10:27 | ||
图片预览



文档简介
八年级数学人教版下册第18章《平行四边形》
经典常考题专题训练(一)
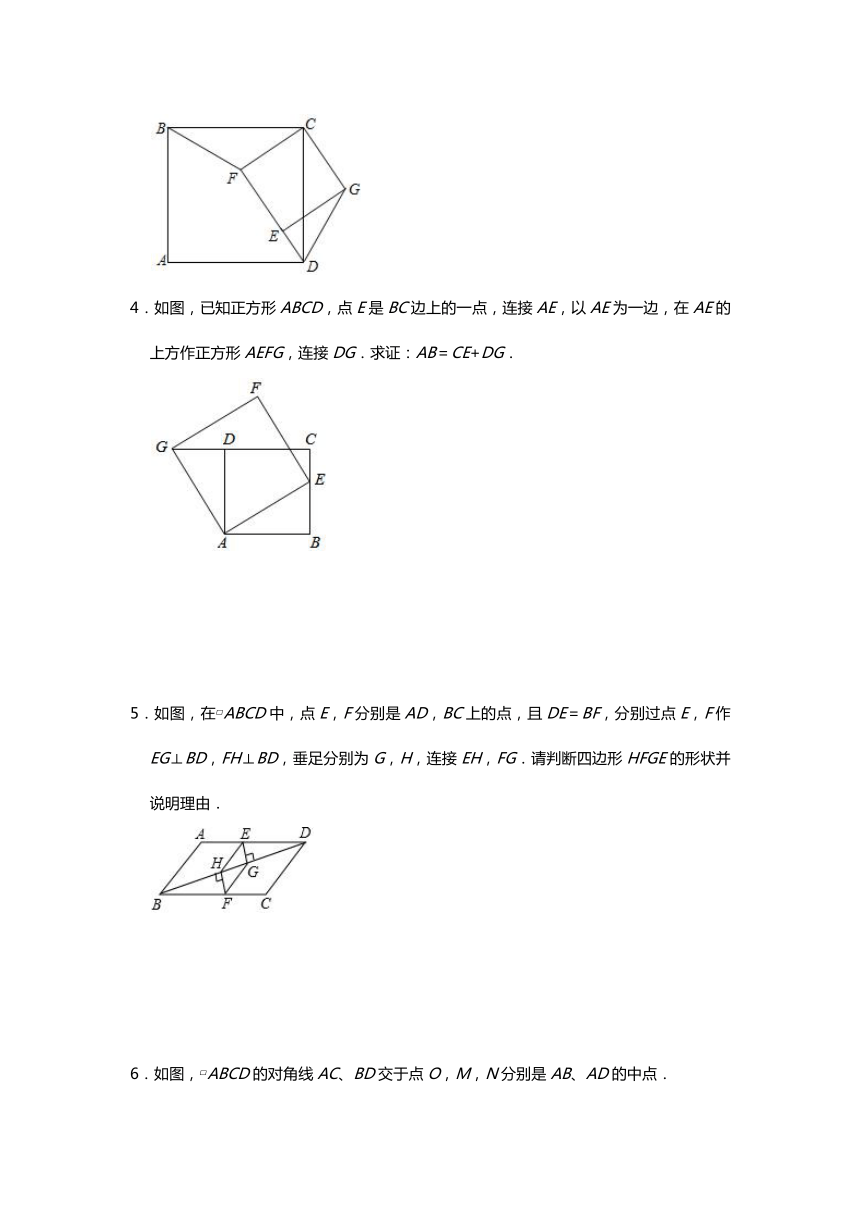
1.如图,在平行四边形ABCD中,对角线AC和BD交于点O,点E、F分别为OA、OC的中点,连接BE、DF、DE.
(1)求证:△ABE≌△CDF;
(2)若BD=2AB,且AB=10,CF=6,直接写出DE的长为
.
2.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,连接AE,若BE=3,AF=5,求AB的长.
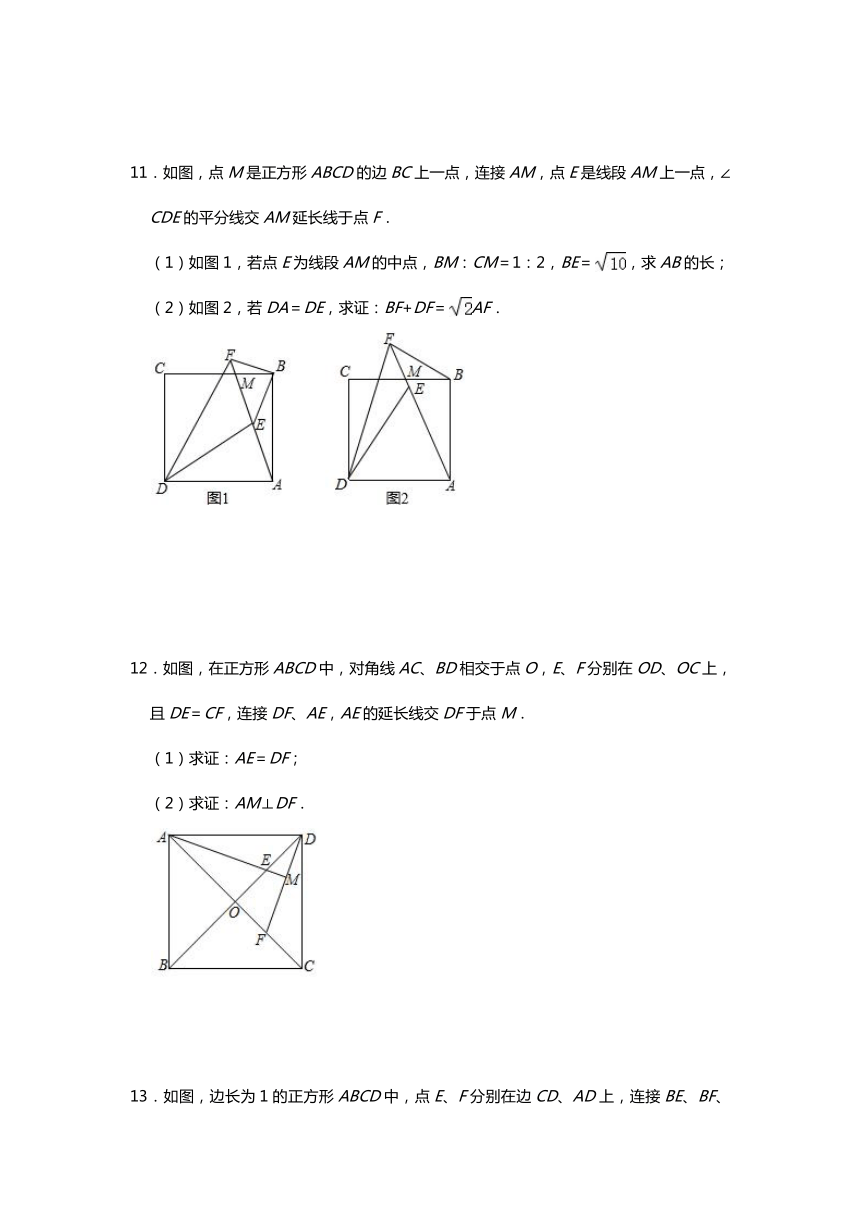
3.如图,已知四边形ABCD和四边形EFCG都是正方形.求证:∠CBF=∠CDG.
4.如图,已知正方形ABCD,点E是BC边上的一点,连接AE,以AE为一边,在AE的上方作正方形AEFG,连接DG.求证:AB=CE+DG.
5.如图,在?ABCD中,点E,F分别是AD,BC上的点,且DE=BF,分别过点E,F作EG⊥BD,FH⊥BD,垂足分别为G,H,连接EH,FG.请判断四边形HFGE的形状并说明理由.
6.如图,?ABCD的对角线AC、BD交于点O,M,N分别是AB、AD的中点.
(1)求证:四边形AMON是平行四边形;
(2)若AC=6,BD=4,∠AOB=90°,求四边形AMON的周长.
7.已知,△ABC、△ADE是等腰三角形,AB=AC,AD=AE,D是BC上一点,∠DAE=∠BAC,过点E作BC的平行线交AB于点F,连接CF.
(1)如图1,求证:四边形CDEF是平行四边形;
(2)如图2,连接BE、DF,若AD⊥BC,在不添加任何辅助线的情况下,请直接写出图2中长度等于BC的长的的线段.
8.如图,点E在矩形ABCD的边BC上,延长EB到点F,使BF=CE,连接AF.求证:AD=EF.
9.如图,在?ABCD中,点P在对角线AC上一动点,过点P作PM∥DC,且PM=DC,连接BM,CM,AP,BD.
(1)求证:△ADP≌△BCM;
(2)若PA=PC,设△ABP的面积为S,四边形BPCM的面积为T,求的值.
10.已知:在?ABCD中,作对角线BD的垂直平分线EF,垂足为点O,分别交AD,BC于点E,F,连接BE,DF.
(1)如图1,求证:四边形BFDE是菱形;
(2)如图2,当∠ABC=90°,且AE=OF时,在不添加任何辅助线情况下,请直接写出图2中的四条线段,使写出的每条线段长度都等于OE长度的倍.
11.如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=,求AB的长;
(2)如图2,若DA=DE,求证:BF+DF=AF.
12.如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.
(1)求证:AE=DF;
(2)求证:AM⊥DF.
13.如图,边长为1的正方形ABCD中,点E、F分别在边CD、AD上,连接BE、BF、EF,且有AF+CE=EF.
(1)求(AF+1)(CE+1)的值;
(2)探究∠EBF的度数是否为定值,并说明理由.
14.如图,在平行四边形ABCD中,点E是AB边上一点,CE=AB,DF⊥BC,垂足为点F,交CE于点G,连接DE,EF.
(1)求证:∠AED=90°﹣∠DCE;
(2)若点E是AB边的中点,求证:∠EFB=∠DEF.
15.如图,在△ABC中,BD平分∠ABC交AC于D,作DE∥BC交AB于点E,作DF∥AB交BC于点F.
(1)求证:四边形BEDF是菱形;
(2)若∠BDE=15°,∠C=45°,CD=,求DE的长.
参考答案
1.解:(1)∵平行四边形ABCD中,对角线AC与BD交于点O,
∴AO=CO,
又∵点E,F分别为OA、OC的中点,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
∴△ABE≌△CDF(SAS);
(2)∵△ABE≌△CDF,
∴BE=DF,AE=CF,
∵BD=2AB,平行四边形ABCD中,对角线AC与BD交于点O,
∴AB=OB=OD=CD,
∵AB=10,CF=6,
∴AB=OB=OD=CD=10,AE=6,
∵AB=OB,点E、F分别为OA、OC的中点,
∴BE⊥AO,DF⊥CO,AE=CF=EO=OF=6,
∴DF=BE=8,EF=12,
在Rt△DEF中,
DE===4.
2.解:∵EF是AC的垂直平分线,
∴AO=CO,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠OAF=∠OCE,
在△AOF和△COE中,
,
∴△AOF≡△COE(ASA),
∴AF=CE=5,
∵EF是AC的垂直平分线,
∴AE=CE=5,
Rt△ABE中,∵BE=3,
∴AB==4.
3.证明:∵四边形ABCD和四边形EFCG都是正方形,
∴CB=CD,CF=CG,∠BCD=∠FCG=90°,
∴∠BCF+∠DCF=∠DCF+∠DCG=90°,
∴∠BCF=∠DCG,
在△BCF和△DCG中,
,
∴△BCF≌△DCG(SAS),
∴∠CBF=∠CDG.
4.证明:∵四边形ABCD和四边形AEFG均是正方形,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∴∠BAE=∠DAG,
∴△ABE≌△ADG(SAS);
∴BE=DG.
∵AB=BC=CE+EB=CE+DG,
即AB=CE+DG.
5.解:四边形HFCE是平行四边形,理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵EG⊥BD,FH⊥BD,
∴∠DGE=∠EGH=∠BHF=∠FHG=90°,
∴EG∥FH,
∵DE=BF,
∴△DGE≌△BHF(AAS),
∴GE=HF,
∴四边形HFCE是平行四边形.
6.(1)根据平行四边形的性质得到AO=OC,BO=OD,AB∥CD,AD∥BC,
由三角形的中位线的性质得到MO∥BC,NO∥CD,
∴MO∥AN,NO∥AM,
∴四边形AMON是平行四边形;
(2)解:∵AC=6,BD=4,
∴AO=3,BO=2,
∵∠AOB=90°,
∴AB===,
∴OM=AM=MB=,
∴NO=AN=,
四边形AMON的周长=AM+OM+AN+NO=2.
7.(1)如答图1,证明:连接BE,
∵∠BAC=∠DAE,
∴∠DAC=∠EAB,
在△ACD和△ABE中,
,
∴△ACD≌△ABE(SAS),
∴CD=BE,∠ACD=∠ABE,
∵EF∥BC,
∴∠ABC=∠EFB,
∴∠ABE=∠EFB,
∴EB=EF,
∴EF=CD,
∵EF∥BC,
∴四边形EDCF是平行四边形;
(2)∵AB=AC,AD⊥BC,
∴BD=CD=BC,
由(1)知CD=BE=EF,
∴BD=EF,
∵E作BC的平行线交AB于点F,即BD||EF,
∴四边形BEFD是平行四边形,
∴BE=DF,
∴BD=CD=BE=EF=DF=BC,
故答案为:BD,CD,BE,EF,DF.
8.证明:∵四边形ABCD是矩形,
∴AD=BC,
∵EF=BF+BE,
∵BC=CE+BE,BF=CE,
∴EF=BC,
∴AD=EF.
9.解:(1)∵PM∥DC,且PM=DC,
∴四边形CDPM是平行四边形,
∴PD=MC,
∵AB∥DC,且AB=DC,PM∥DC,且PM=DC,
∴AB∥PM,且AB=PM,
∴四边形ABMP是平行四边形,
∴AP=BM,
∵四边形ABCD是平行四边形,
∴AD=BC,
∴△ADP≌△BCM(SSS);
(2)由(1)可得S△ADP=S△BCM,
∴S四边形BMCP=S△BCM+S△BCP=S△ADP+S△BCP=S平行四边形ABCD,
又∵PA=PC,
∴S△ABP=S△ABC=S平行四边形ABCD,
∴的值为=.
10.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠EDO=∠FBO,
∵EF垂直平分BD,
∴OB=OD,
在△EOD和△FOB中,,
∴△DOE≌△BOF(ASA);
∴OE=OF,
又∵OB=OD,
∴四边形EBFD是平行四边形,
∵EF⊥BD,
∴四边形BFDE为菱形.
(2)解:AB、CD、OB、OD四条线段都等于OE长度的倍,理由如下:
由(1)得:OE=OF,∠OBE=∠OBF,
∵AE=OF,
∴AE=OE,
∵?ABCD中,∠ABC=90°,
∴四边形ABCD是矩形,
∴∠A=90°,
∵EF⊥BD,
∴∠BOE=90°,
在Rt△BAE和Rt△BOE中,,
∴Rt△BAE≌Rt△BOE(HL),
∴AB=OB=OD,∠ABE=∠OBE=∠OBF,
∵∠ABC=90°,
∴∠ABE=30°,
∴AB=AE=OE,
∴AB=CD=OB=OD=OE.
11.解:(1)设BM=x,则CM=2x,BC=3x,
∵BA=BC,∴BA=3x.
在Rt△ABM中,E为斜边AM中点,
∴AM=2BE=2.
由勾股定理可得AM2=MB2+AB2,
即40=x2+9x2,解得x=2.
∴AB=3x=6.
(2)延长FD交过点A作垂直于AF的直线于H点,过点D作DP⊥AF于P点.
∵DF平分∠CDE,
∴∠1=∠2.
∵DE=DA,DP⊥AF
∴∠3=∠4.
∵∠1+∠2+∠3+∠4=90°,
∴∠2+∠3=45°.
∴∠DFP=90°﹣45°=45°.
∴AH=AF.
∵∠BAF+∠DAF=90°,∠HAD+∠DAF=90°,
∴∠BAF=∠DAH.
又AB=AD,
∴△ABF≌△ADH(SAS).
∴AF=AH,BF=DH.
∵Rt△FAH是等腰直角三角形,
∴HF=AF.
∵HF=DH+DF=BF+DF,
∴BF+DF=AF.
12.证明:(1)∵四边形ABCD是正方形,
∴OA=CO=OD,AC⊥BD,
∴∠AOE=∠DOF=90°,
又∵DE=CF,
∴OD﹣DE=OC﹣CF,
即OE=OF,
在△AOE和△DOF中,,
∴△AOE≌△DOF(SAS),
∴AE=DF;
(2)由(1)得:△AOE≌△DOF,
∴∠OEA=∠OFD,
∵∠OAE+∠AEO=90°,
∴∠OAE+∠OFD=90°,
∴∠AMF=90°,
∴AM⊥DF.
13.解:(1)设CE=x,AF=y,则DE=1﹣x,DF=1﹣y,
∵AF+CE=EF,
∴EF=x+y.
∵四边形ABCD是正方形,
∴∠D=90°,
∴EF2=DE2+DF2,即(x+y)2=(1﹣x)2+(1﹣y)2,
∴xy+x+y=1,
∴(AF+1)(CE+1)=(y+1)(x+1)=xy+x+y+1=1+1=2;
(2)∠EBF的度数为定值,理由如下:
如图,将△ABF绕点B顺时针旋转90°得到△BCM,此时AB与CB重合.
由旋转,可得:AB=CB,BF=BM,AF=CM,∠ABF=∠CBM,∠BCM=∠A=90°,
∴∠BCM+∠BCD=90°+90°=180°,
∴点M、C、E在同一条直线上.
∵AF+CE=EF,CM+CE=EM,
∴EF=EM.
在△BEF和△BEM中,,
∴△BEF≌△BEM(SSS),
∴∠EBF=∠EBM=∠CBM+∠CBE=∠ABF+∠CBE,
又∵∠ABC=90°,∠ABC=∠EBF+∠ABF+∠CBE,
∴∠EBF=∠ABC=45°.
14.证明:(1)∵CE=AB,AB=CD
∴CE=CD,
∴∠CDE=∠CED==90°﹣∠DCE,
∵CD∥AB
∴∠AED=∠CDE=90°﹣∠DCE;
(2)如图,延长DA,FE于点M,
∵四边形ABCD是平行四边形
∴AD∥BC,且DF⊥BC
∴DF⊥AD,∠M=∠EFB
∵∠M=∠EFB,AE=BE,∠AEM=∠FEB
∴△AEM≌△BEF(AAS)
∴ME=EF,且DF⊥DM
∴ME=DE=EF
∴∠M=∠MDE
∴∠DEF=∠M+∠MDE=2∠M
∴∠EFB=∠DEF
15.证明:(1)∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵DE∥BC,
∴∠EDB=∠DBC,
∴∠EBD=∠EDB,
∴BE=ED,
∴BE=DE,
同理可得:BF=DF,
∵∠EBD=∠EDB,∠FBD=∠FDB,
∴∠EBD=∠BDF,∠EDB=∠DBF,
∴BE∥DF,DE∥BF,
∴四边形DEBF是平行四边形,且BE=DE,
∴四边形BEDF是菱形;
(2)过点D作DH⊥BC于点H,
∵四边形BEDF是菱形,
∴BF=DF=DE,EF垂直平分BD,
∴∠FBD=∠FDB=∠BDE=15°,
∴∠DFH=30°,且DH⊥BC,
∴DH=DF,FH=DH,
∵∠C=45°,DH⊥BC,
∴∠C=∠CDH=45°,
∴DH=CH=,
∴FC=FH+CH=,
∴DF=2,
∴DE=2.
经典常考题专题训练(一)
1.如图,在平行四边形ABCD中,对角线AC和BD交于点O,点E、F分别为OA、OC的中点,连接BE、DF、DE.
(1)求证:△ABE≌△CDF;
(2)若BD=2AB,且AB=10,CF=6,直接写出DE的长为
.
2.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,连接AE,若BE=3,AF=5,求AB的长.
3.如图,已知四边形ABCD和四边形EFCG都是正方形.求证:∠CBF=∠CDG.
4.如图,已知正方形ABCD,点E是BC边上的一点,连接AE,以AE为一边,在AE的上方作正方形AEFG,连接DG.求证:AB=CE+DG.
5.如图,在?ABCD中,点E,F分别是AD,BC上的点,且DE=BF,分别过点E,F作EG⊥BD,FH⊥BD,垂足分别为G,H,连接EH,FG.请判断四边形HFGE的形状并说明理由.
6.如图,?ABCD的对角线AC、BD交于点O,M,N分别是AB、AD的中点.
(1)求证:四边形AMON是平行四边形;
(2)若AC=6,BD=4,∠AOB=90°,求四边形AMON的周长.
7.已知,△ABC、△ADE是等腰三角形,AB=AC,AD=AE,D是BC上一点,∠DAE=∠BAC,过点E作BC的平行线交AB于点F,连接CF.
(1)如图1,求证:四边形CDEF是平行四边形;
(2)如图2,连接BE、DF,若AD⊥BC,在不添加任何辅助线的情况下,请直接写出图2中长度等于BC的长的的线段.
8.如图,点E在矩形ABCD的边BC上,延长EB到点F,使BF=CE,连接AF.求证:AD=EF.
9.如图,在?ABCD中,点P在对角线AC上一动点,过点P作PM∥DC,且PM=DC,连接BM,CM,AP,BD.
(1)求证:△ADP≌△BCM;
(2)若PA=PC,设△ABP的面积为S,四边形BPCM的面积为T,求的值.
10.已知:在?ABCD中,作对角线BD的垂直平分线EF,垂足为点O,分别交AD,BC于点E,F,连接BE,DF.
(1)如图1,求证:四边形BFDE是菱形;
(2)如图2,当∠ABC=90°,且AE=OF时,在不添加任何辅助线情况下,请直接写出图2中的四条线段,使写出的每条线段长度都等于OE长度的倍.
11.如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM:CM=1:2,BE=,求AB的长;
(2)如图2,若DA=DE,求证:BF+DF=AF.
12.如图,在正方形ABCD中,对角线AC、BD相交于点O,E、F分别在OD、OC上,且DE=CF,连接DF、AE,AE的延长线交DF于点M.
(1)求证:AE=DF;
(2)求证:AM⊥DF.
13.如图,边长为1的正方形ABCD中,点E、F分别在边CD、AD上,连接BE、BF、EF,且有AF+CE=EF.
(1)求(AF+1)(CE+1)的值;
(2)探究∠EBF的度数是否为定值,并说明理由.
14.如图,在平行四边形ABCD中,点E是AB边上一点,CE=AB,DF⊥BC,垂足为点F,交CE于点G,连接DE,EF.
(1)求证:∠AED=90°﹣∠DCE;
(2)若点E是AB边的中点,求证:∠EFB=∠DEF.
15.如图,在△ABC中,BD平分∠ABC交AC于D,作DE∥BC交AB于点E,作DF∥AB交BC于点F.
(1)求证:四边形BEDF是菱形;
(2)若∠BDE=15°,∠C=45°,CD=,求DE的长.
参考答案
1.解:(1)∵平行四边形ABCD中,对角线AC与BD交于点O,
∴AO=CO,
又∵点E,F分别为OA、OC的中点,
∴AE=CF,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
∴△ABE≌△CDF(SAS);
(2)∵△ABE≌△CDF,
∴BE=DF,AE=CF,
∵BD=2AB,平行四边形ABCD中,对角线AC与BD交于点O,
∴AB=OB=OD=CD,
∵AB=10,CF=6,
∴AB=OB=OD=CD=10,AE=6,
∵AB=OB,点E、F分别为OA、OC的中点,
∴BE⊥AO,DF⊥CO,AE=CF=EO=OF=6,
∴DF=BE=8,EF=12,
在Rt△DEF中,
DE===4.
2.解:∵EF是AC的垂直平分线,
∴AO=CO,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠OAF=∠OCE,
在△AOF和△COE中,
,
∴△AOF≡△COE(ASA),
∴AF=CE=5,
∵EF是AC的垂直平分线,
∴AE=CE=5,
Rt△ABE中,∵BE=3,
∴AB==4.
3.证明:∵四边形ABCD和四边形EFCG都是正方形,
∴CB=CD,CF=CG,∠BCD=∠FCG=90°,
∴∠BCF+∠DCF=∠DCF+∠DCG=90°,
∴∠BCF=∠DCG,
在△BCF和△DCG中,
,
∴△BCF≌△DCG(SAS),
∴∠CBF=∠CDG.
4.证明:∵四边形ABCD和四边形AEFG均是正方形,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∴∠BAE=∠DAG,
∴△ABE≌△ADG(SAS);
∴BE=DG.
∵AB=BC=CE+EB=CE+DG,
即AB=CE+DG.
5.解:四边形HFCE是平行四边形,理由如下:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADB=∠CBD,
∵EG⊥BD,FH⊥BD,
∴∠DGE=∠EGH=∠BHF=∠FHG=90°,
∴EG∥FH,
∵DE=BF,
∴△DGE≌△BHF(AAS),
∴GE=HF,
∴四边形HFCE是平行四边形.
6.(1)根据平行四边形的性质得到AO=OC,BO=OD,AB∥CD,AD∥BC,
由三角形的中位线的性质得到MO∥BC,NO∥CD,
∴MO∥AN,NO∥AM,
∴四边形AMON是平行四边形;
(2)解:∵AC=6,BD=4,
∴AO=3,BO=2,
∵∠AOB=90°,
∴AB===,
∴OM=AM=MB=,
∴NO=AN=,
四边形AMON的周长=AM+OM+AN+NO=2.
7.(1)如答图1,证明:连接BE,
∵∠BAC=∠DAE,
∴∠DAC=∠EAB,
在△ACD和△ABE中,
,
∴△ACD≌△ABE(SAS),
∴CD=BE,∠ACD=∠ABE,
∵EF∥BC,
∴∠ABC=∠EFB,
∴∠ABE=∠EFB,
∴EB=EF,
∴EF=CD,
∵EF∥BC,
∴四边形EDCF是平行四边形;
(2)∵AB=AC,AD⊥BC,
∴BD=CD=BC,
由(1)知CD=BE=EF,
∴BD=EF,
∵E作BC的平行线交AB于点F,即BD||EF,
∴四边形BEFD是平行四边形,
∴BE=DF,
∴BD=CD=BE=EF=DF=BC,
故答案为:BD,CD,BE,EF,DF.
8.证明:∵四边形ABCD是矩形,
∴AD=BC,
∵EF=BF+BE,
∵BC=CE+BE,BF=CE,
∴EF=BC,
∴AD=EF.
9.解:(1)∵PM∥DC,且PM=DC,
∴四边形CDPM是平行四边形,
∴PD=MC,
∵AB∥DC,且AB=DC,PM∥DC,且PM=DC,
∴AB∥PM,且AB=PM,
∴四边形ABMP是平行四边形,
∴AP=BM,
∵四边形ABCD是平行四边形,
∴AD=BC,
∴△ADP≌△BCM(SSS);
(2)由(1)可得S△ADP=S△BCM,
∴S四边形BMCP=S△BCM+S△BCP=S△ADP+S△BCP=S平行四边形ABCD,
又∵PA=PC,
∴S△ABP=S△ABC=S平行四边形ABCD,
∴的值为=.
10.(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC,
∴∠EDO=∠FBO,
∵EF垂直平分BD,
∴OB=OD,
在△EOD和△FOB中,,
∴△DOE≌△BOF(ASA);
∴OE=OF,
又∵OB=OD,
∴四边形EBFD是平行四边形,
∵EF⊥BD,
∴四边形BFDE为菱形.
(2)解:AB、CD、OB、OD四条线段都等于OE长度的倍,理由如下:
由(1)得:OE=OF,∠OBE=∠OBF,
∵AE=OF,
∴AE=OE,
∵?ABCD中,∠ABC=90°,
∴四边形ABCD是矩形,
∴∠A=90°,
∵EF⊥BD,
∴∠BOE=90°,
在Rt△BAE和Rt△BOE中,,
∴Rt△BAE≌Rt△BOE(HL),
∴AB=OB=OD,∠ABE=∠OBE=∠OBF,
∵∠ABC=90°,
∴∠ABE=30°,
∴AB=AE=OE,
∴AB=CD=OB=OD=OE.
11.解:(1)设BM=x,则CM=2x,BC=3x,
∵BA=BC,∴BA=3x.
在Rt△ABM中,E为斜边AM中点,
∴AM=2BE=2.
由勾股定理可得AM2=MB2+AB2,
即40=x2+9x2,解得x=2.
∴AB=3x=6.
(2)延长FD交过点A作垂直于AF的直线于H点,过点D作DP⊥AF于P点.
∵DF平分∠CDE,
∴∠1=∠2.
∵DE=DA,DP⊥AF
∴∠3=∠4.
∵∠1+∠2+∠3+∠4=90°,
∴∠2+∠3=45°.
∴∠DFP=90°﹣45°=45°.
∴AH=AF.
∵∠BAF+∠DAF=90°,∠HAD+∠DAF=90°,
∴∠BAF=∠DAH.
又AB=AD,
∴△ABF≌△ADH(SAS).
∴AF=AH,BF=DH.
∵Rt△FAH是等腰直角三角形,
∴HF=AF.
∵HF=DH+DF=BF+DF,
∴BF+DF=AF.
12.证明:(1)∵四边形ABCD是正方形,
∴OA=CO=OD,AC⊥BD,
∴∠AOE=∠DOF=90°,
又∵DE=CF,
∴OD﹣DE=OC﹣CF,
即OE=OF,
在△AOE和△DOF中,,
∴△AOE≌△DOF(SAS),
∴AE=DF;
(2)由(1)得:△AOE≌△DOF,
∴∠OEA=∠OFD,
∵∠OAE+∠AEO=90°,
∴∠OAE+∠OFD=90°,
∴∠AMF=90°,
∴AM⊥DF.
13.解:(1)设CE=x,AF=y,则DE=1﹣x,DF=1﹣y,
∵AF+CE=EF,
∴EF=x+y.
∵四边形ABCD是正方形,
∴∠D=90°,
∴EF2=DE2+DF2,即(x+y)2=(1﹣x)2+(1﹣y)2,
∴xy+x+y=1,
∴(AF+1)(CE+1)=(y+1)(x+1)=xy+x+y+1=1+1=2;
(2)∠EBF的度数为定值,理由如下:
如图,将△ABF绕点B顺时针旋转90°得到△BCM,此时AB与CB重合.
由旋转,可得:AB=CB,BF=BM,AF=CM,∠ABF=∠CBM,∠BCM=∠A=90°,
∴∠BCM+∠BCD=90°+90°=180°,
∴点M、C、E在同一条直线上.
∵AF+CE=EF,CM+CE=EM,
∴EF=EM.
在△BEF和△BEM中,,
∴△BEF≌△BEM(SSS),
∴∠EBF=∠EBM=∠CBM+∠CBE=∠ABF+∠CBE,
又∵∠ABC=90°,∠ABC=∠EBF+∠ABF+∠CBE,
∴∠EBF=∠ABC=45°.
14.证明:(1)∵CE=AB,AB=CD
∴CE=CD,
∴∠CDE=∠CED==90°﹣∠DCE,
∵CD∥AB
∴∠AED=∠CDE=90°﹣∠DCE;
(2)如图,延长DA,FE于点M,
∵四边形ABCD是平行四边形
∴AD∥BC,且DF⊥BC
∴DF⊥AD,∠M=∠EFB
∵∠M=∠EFB,AE=BE,∠AEM=∠FEB
∴△AEM≌△BEF(AAS)
∴ME=EF,且DF⊥DM
∴ME=DE=EF
∴∠M=∠MDE
∴∠DEF=∠M+∠MDE=2∠M
∴∠EFB=∠DEF
15.证明:(1)∵BD平分∠ABC,
∴∠ABD=∠DBC,
∵DE∥BC,
∴∠EDB=∠DBC,
∴∠EBD=∠EDB,
∴BE=ED,
∴BE=DE,
同理可得:BF=DF,
∵∠EBD=∠EDB,∠FBD=∠FDB,
∴∠EBD=∠BDF,∠EDB=∠DBF,
∴BE∥DF,DE∥BF,
∴四边形DEBF是平行四边形,且BE=DE,
∴四边形BEDF是菱形;
(2)过点D作DH⊥BC于点H,
∵四边形BEDF是菱形,
∴BF=DF=DE,EF垂直平分BD,
∴∠FBD=∠FDB=∠BDE=15°,
∴∠DFH=30°,且DH⊥BC,
∴DH=DF,FH=DH,
∵∠C=45°,DH⊥BC,
∴∠C=∠CDH=45°,
∴DH=CH=,
∴FC=FH+CH=,
∴DF=2,
∴DE=2.
