2020—2021学年北师大版数学七年级下册第二章相交线和平行线基础复习试题(word版无答案)
文档属性
| 名称 | 2020—2021学年北师大版数学七年级下册第二章相交线和平行线基础复习试题(word版无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 366.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-04-04 13:35:38 | ||
图片预览


文档简介
第二章:相交线与平行线复习
基础知识
一、两直线的位置关系有两种:相交(垂直)
平行
二、两直线被第三条直线所截产生的各类角概念及性质
1.同位角
内错角
同旁内角的定义
2.邻补角和对顶角的性质
(1)邻补角互补
(2)对顶角相等
注:“同”指两角位于第三直线的同侧,“错”指两角位于第三直线两侧
,“内”指两角位于两被截直线之间
三、垂线
点到直线的距离
1.垂线的概念:两条直线相交,若其所形成的四个角中有一个角等于
90°,
则称这两条直线互相垂直,其中一条直线叫做另一条直线的
垂线,他们的交点叫做垂足
注:
垂直是相交的一种特殊情形
两直线垂直必具备两个要点:A.相交
B.有一个角为直角
2.垂线的性质:
(1)在平面门内,过一点有且只有一条直线与已知直线垂直
(2)连接直线外一点与直线上各点的所有县段中,垂线段最短
四、平行线
1.平行线的概念:在同一平面内,不相交的两条直线叫做平行线
注:平行的前提是两直线在同一平面内
2.平行公理
(1)经过直线外一点,有且只有一条直线与这条直线平行
(2)如果两条直线都与第三条直线平行,那么着两条直线也互相平行,
即如果
a∥b,b∥c,那么
a∥c
,也叫平行线的传递性。
3.平行线的性质
(1)两条平行直线被第三条直线所截,同位角相等
(2)两条平行直线被第三条直线所截,内错角相等
(3)两条平行直线被第三条直线所截,同旁内角互补
4.平行线的距离:同时垂直于两条平行线,并且夹在平行线间的线段的长度,叫做这两条平行线间的距离
5.平行线的判定
如果两直线被第三条直线所截:
(1)
同位角相等,两直线平行
(2)
内错角相等,两直线平行
(3)
同旁内角互补,两直线平行
考点1:相交线
1.在同一个平面内,不重合的两条直线的位置关系可能是
(
)
A.相交或平行
B.相交或垂直
C.平行或垂直
D.不能确定
2.在同一平面内的
n
条直线两两相交,最多共有
36
个交点,则
n=(
)
A.7
B.8
C.9
D.10
3.同一平面内两两相交的四条直线,最多有
m
个交点,最少有
n
个交点,那么
mn
是(
)
A.1
B.6
C.8
D.4
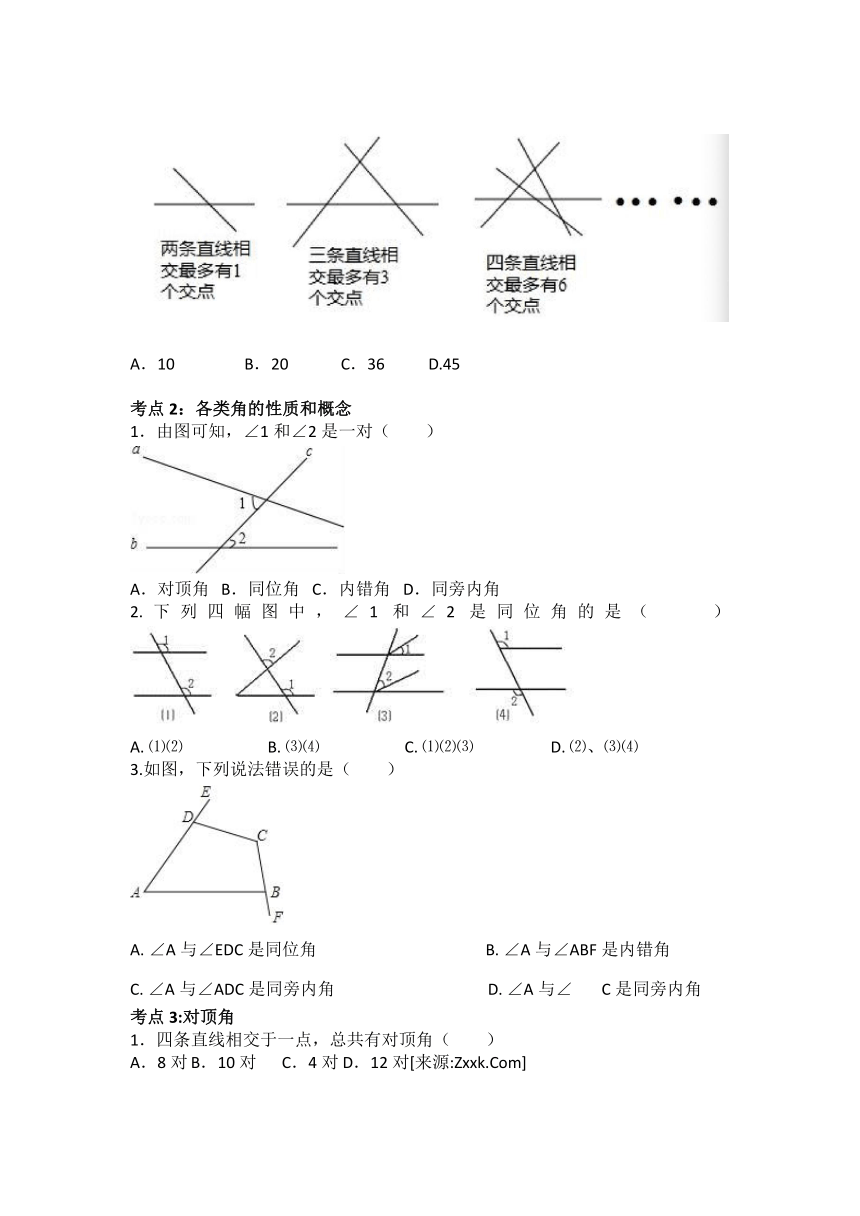
4.观察如图图形,并阅读相关文字:那么
10
条直线相交,最多交点的个数是
(
)
A.10
B.20
C.36
D.45
考点2:各类角的性质和概念
1.由图可知,∠1和∠2是一对( )
A.对顶角
B.同位角
C.内错角
D.同旁内角
2.下列四幅图中,∠1和∠2是同位角的是( )
A.?⑴⑵?????????????????????B.?⑶⑷?????????????????????C.?⑴⑵⑶???????????????????D.?⑵、⑶⑷
3.如图,下列说法错误的是( )
?
A.?∠A与∠EDC是同位角???????????????????????????????????????????B.?∠A与∠ABF是内错角
C.?∠A与∠ADC是同旁内角???????????????????????????????????????D.?∠A与∠C是同旁内角
考点3:对顶角
1.四条直线相交于一点,总共有对顶角( )
A.8对
B.10对
C.4对
D.12对[]
考点4:邻补角
1.如果一个角的余角是30°,那么这个角是________?.
2.已知∠α的补角是它的3倍,则∠α=________.
3.一个角的补角加上24°,恰好等于这个角的5倍,求这个角的度数.
4.∠1
与∠2
互余且相等,∠1
与∠3
是邻补角,则∠3
的大小是(
)
A.30°
B.105°
C.120°
D.135°
5.已知∠A=25°,则∠A的余角、补角分别是
(
)
A.65°
B.75°
C.155°
D.165°
考点5:平行线的性质
1、如图,已知直线AB,CD被直线EF所截,如果AB∥CD,那么( )
A.∠1>∠2
B.∠1=∠2
C.∠1<∠2
D.∠1+∠2=180°
2.下列说法:①在同一平面内,不相交的两条线段叫做平行线;②过一点,有且只有一条直线平行于已知直线;③两条平行直线被第三条直线所截,同位角相等;④同旁内角相等,两直线平行.正确的个数有( )个.
A.?1????????????????????????????B.?2????????????????????????C.?3????????????????????????????????D.?4
3.a,b,c是直线,且a∥b,b∥c,则________?.
4.如图,∠1=75°,∠2=120°,∠3=75°,则∠4=________?
5.如图,直线l1∥l2
,
并且被直线l3
,
l4所截,则∠α=________?
6.如图,AB∥CD
,
则图中∠1、∠2、∠3关系一定成立的是(????)?????
???????
A.?∠1+∠2+∠3=180°???????????B.?∠1+∠2+∠3=360°????????
?C.?∠1+∠3=2∠2?????
??????D.?∠1+∠3=∠2
7.如图,AB∥GF,则∠ABC+∠C+∠D+∠E+∠EFG=
.若∠ABH=30°,∠MFG=28°,则∠H+∠L+∠M=
.
8.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
∵AB∥DC(已知)
∴∠1=∠CFE(________)
∵AE平分∠BAD(已知)
∴∠1=∠2
(角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=________(等量代换)
∴AD∥BC
(________)
考点6:垂线段最短
1.如果直线MN外一点A到直线MN的距离是3cm,那么点A与直线MN上任意一点B所连成的线段AB的长度一定是( )
A.3cm
B.小于3cm
C.大于3cm
D.大于或等于3cm
2.如图,是一条河,C是河边AB外一点:
(1)过点C要修一条与河平行的绿化带,请作出正确的示意图.
(2)现欲用水管从河边AB,将水引到C处,请在图上测量并计算出水管至少要多少?(本图比例尺为1:2000)
3.下列作图能表示点A到BC的距离的是
(
)
A.
B.
C.
D.
考点7:平行线的判定
1.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是(?
)
A.?同位角相等,两直线平行????????????????????????????????????B.?内错角相等,两直线平行
C.?同旁内角互补,两直线平行????????????????????????????????D.?两直线平行,同位角相等
2.如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是(??
)
A.?AB∥CD∥EF??????B.?CD∥EF??????????C.?AB∥EF??????????D.?AB∥CD∥EF,BC∥DE
3.如图,在△ABC中,CD⊥AB,垂足为点D,点E在BC上,EF⊥AB,垂足为F;
(1)
CD与EF平行吗?为什么?
(2)
如果∠1=∠2,且∠3=105°,求∠ACB的度数;
4.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
∵AB∥DC(已知)
∴∠1=∠CFE(________)
∵AE平分∠BAD(已知)
∴∠1=∠2
(角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=________(等量代换)
∴AD∥BC
(________)
基础知识
一、两直线的位置关系有两种:相交(垂直)
平行
二、两直线被第三条直线所截产生的各类角概念及性质
1.同位角
内错角
同旁内角的定义
2.邻补角和对顶角的性质
(1)邻补角互补
(2)对顶角相等
注:“同”指两角位于第三直线的同侧,“错”指两角位于第三直线两侧
,“内”指两角位于两被截直线之间
三、垂线
点到直线的距离
1.垂线的概念:两条直线相交,若其所形成的四个角中有一个角等于
90°,
则称这两条直线互相垂直,其中一条直线叫做另一条直线的
垂线,他们的交点叫做垂足
注:
垂直是相交的一种特殊情形
两直线垂直必具备两个要点:A.相交
B.有一个角为直角
2.垂线的性质:
(1)在平面门内,过一点有且只有一条直线与已知直线垂直
(2)连接直线外一点与直线上各点的所有县段中,垂线段最短
四、平行线
1.平行线的概念:在同一平面内,不相交的两条直线叫做平行线
注:平行的前提是两直线在同一平面内
2.平行公理
(1)经过直线外一点,有且只有一条直线与这条直线平行
(2)如果两条直线都与第三条直线平行,那么着两条直线也互相平行,
即如果
a∥b,b∥c,那么
a∥c
,也叫平行线的传递性。
3.平行线的性质
(1)两条平行直线被第三条直线所截,同位角相等
(2)两条平行直线被第三条直线所截,内错角相等
(3)两条平行直线被第三条直线所截,同旁内角互补
4.平行线的距离:同时垂直于两条平行线,并且夹在平行线间的线段的长度,叫做这两条平行线间的距离
5.平行线的判定
如果两直线被第三条直线所截:
(1)
同位角相等,两直线平行
(2)
内错角相等,两直线平行
(3)
同旁内角互补,两直线平行
考点1:相交线
1.在同一个平面内,不重合的两条直线的位置关系可能是
(
)
A.相交或平行
B.相交或垂直
C.平行或垂直
D.不能确定
2.在同一平面内的
n
条直线两两相交,最多共有
36
个交点,则
n=(
)
A.7
B.8
C.9
D.10
3.同一平面内两两相交的四条直线,最多有
m
个交点,最少有
n
个交点,那么
mn
是(
)
A.1
B.6
C.8
D.4
4.观察如图图形,并阅读相关文字:那么
10
条直线相交,最多交点的个数是
(
)
A.10
B.20
C.36
D.45
考点2:各类角的性质和概念
1.由图可知,∠1和∠2是一对( )
A.对顶角
B.同位角
C.内错角
D.同旁内角
2.下列四幅图中,∠1和∠2是同位角的是( )
A.?⑴⑵?????????????????????B.?⑶⑷?????????????????????C.?⑴⑵⑶???????????????????D.?⑵、⑶⑷
3.如图,下列说法错误的是( )
?
A.?∠A与∠EDC是同位角???????????????????????????????????????????B.?∠A与∠ABF是内错角
C.?∠A与∠ADC是同旁内角???????????????????????????????????????D.?∠A与∠C是同旁内角
考点3:对顶角
1.四条直线相交于一点,总共有对顶角( )
A.8对
B.10对
C.4对
D.12对[]
考点4:邻补角
1.如果一个角的余角是30°,那么这个角是________?.
2.已知∠α的补角是它的3倍,则∠α=________.
3.一个角的补角加上24°,恰好等于这个角的5倍,求这个角的度数.
4.∠1
与∠2
互余且相等,∠1
与∠3
是邻补角,则∠3
的大小是(
)
A.30°
B.105°
C.120°
D.135°
5.已知∠A=25°,则∠A的余角、补角分别是
(
)
A.65°
B.75°
C.155°
D.165°
考点5:平行线的性质
1、如图,已知直线AB,CD被直线EF所截,如果AB∥CD,那么( )
A.∠1>∠2
B.∠1=∠2
C.∠1<∠2
D.∠1+∠2=180°
2.下列说法:①在同一平面内,不相交的两条线段叫做平行线;②过一点,有且只有一条直线平行于已知直线;③两条平行直线被第三条直线所截,同位角相等;④同旁内角相等,两直线平行.正确的个数有( )个.
A.?1????????????????????????????B.?2????????????????????????C.?3????????????????????????????????D.?4
3.a,b,c是直线,且a∥b,b∥c,则________?.
4.如图,∠1=75°,∠2=120°,∠3=75°,则∠4=________?
5.如图,直线l1∥l2
,
并且被直线l3
,
l4所截,则∠α=________?
6.如图,AB∥CD
,
则图中∠1、∠2、∠3关系一定成立的是(????)?????
???????
A.?∠1+∠2+∠3=180°???????????B.?∠1+∠2+∠3=360°????????
?C.?∠1+∠3=2∠2?????
??????D.?∠1+∠3=∠2
7.如图,AB∥GF,则∠ABC+∠C+∠D+∠E+∠EFG=
.若∠ABH=30°,∠MFG=28°,则∠H+∠L+∠M=
.
8.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
∵AB∥DC(已知)
∴∠1=∠CFE(________)
∵AE平分∠BAD(已知)
∴∠1=∠2
(角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=________(等量代换)
∴AD∥BC
(________)
考点6:垂线段最短
1.如果直线MN外一点A到直线MN的距离是3cm,那么点A与直线MN上任意一点B所连成的线段AB的长度一定是( )
A.3cm
B.小于3cm
C.大于3cm
D.大于或等于3cm
2.如图,是一条河,C是河边AB外一点:
(1)过点C要修一条与河平行的绿化带,请作出正确的示意图.
(2)现欲用水管从河边AB,将水引到C处,请在图上测量并计算出水管至少要多少?(本图比例尺为1:2000)
3.下列作图能表示点A到BC的距离的是
(
)
A.
B.
C.
D.
考点7:平行线的判定
1.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是(?
)
A.?同位角相等,两直线平行????????????????????????????????????B.?内错角相等,两直线平行
C.?同旁内角互补,两直线平行????????????????????????????????D.?两直线平行,同位角相等
2.如图,已知∠1=∠2=∠3=∠4,则图形中所有平行的是(??
)
A.?AB∥CD∥EF??????B.?CD∥EF??????????C.?AB∥EF??????????D.?AB∥CD∥EF,BC∥DE
3.如图,在△ABC中,CD⊥AB,垂足为点D,点E在BC上,EF⊥AB,垂足为F;
(1)
CD与EF平行吗?为什么?
(2)
如果∠1=∠2,且∠3=105°,求∠ACB的度数;
4.如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E.试说明AD∥BC.完成推理过程:
∵AB∥DC(已知)
∴∠1=∠CFE(________)
∵AE平分∠BAD(已知)
∴∠1=∠2
(角平分线的定义)
∵∠CFE=∠E(已知)
∴∠2=________(等量代换)
∴AD∥BC
(________)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
